考虑调整时间的绿色柔性作业车间调度研究*
卫少鹏,王 婷,2*,周 彤
(1.贵州大学 管理学院,贵州 贵阳 550025;2.贵州省“互联网+”协同智能制造重点实验室,贵州 贵阳 550025)
0 引 言
绿色车间调度作为绿色制造的重要依托技术,通过合理分配资源、调整加工顺序,达到节能减排、降低成本的目标。在实际生产过程中,装夹、对刀等辅助操作所消耗的时间和能量占据较大比例,探明调整环节在绿色作业车间调度中对完工时间和能耗的影响具有重要意义,能够更加有效地指导柔性作业车间的绿色生产。
在模型建立层面,绿色车间调度模型在保证经济指标正常运行的同时,还要兼顾绿色指标的优化约束,属于多目标优化模型。根据处理方法的不同,模型可以分为两类:加权优化模型和帕累托优化模型。
(1)在加权模型的研究中,DAI等[1]考虑到生产对环境的影响,选取能耗和完工时间作为优化指标,利用加权法将两个指标合并为单个指标,采用单目标算法对模型进行了求解;解潇晗等[2]针对柔性作业车间的节能调度问题,选取能耗作为绿色指标,降低了运行过程中的切削能耗、负载能耗等;王建华等[3]针对具有机器柔性和折旧特性的调度问题,同时考虑机器启动、负载、空转、停止环节消耗的能耗,通过为工序匹配相对节能的机器,降低了生产过程中的能耗。
(2)在帕累托模型的研究中,张斯琪等[4]以完工时间为经济指标,以能耗浪费和噪音污染为绿色指标,建立了绿色车间调度模型;ZHANG等[5]以最大完工时间、相邻工件完工时间间隔、机器负载和碳排放量优化指标,并考虑了机器加工、辅助材料、工具磨损和运输过程的碳排放;吴秀丽等[6]从考虑机器转速的角度进行了节能调度研究,构建了带有多机器转速的生产模型。
综上所述,大多数研究集中在加工环节,如:时间、能耗、噪音、机器负载、机器转速等因素,较少考虑到加工辅助环节,如:机器调整、物料运输、生产准备等工艺过程,尤其机器调整环节的装夹、定位、对刀、测量等辅助操作,消耗了大量的时间、能源和人资,对绿色生产具有较大影响。因此,对此进行深入研究能够更好地发掘制造企业节能减排的潜力。
在算法设计层面,目前对经典智能算法的引用和改进较为普遍。其中,裴小兵等[7]提出了基于三方博弈的改进遗传算法,通过完工时间、总机器负荷和临界机器负荷3个目标间的博弈得到了帕累托最优解;杨振泰等[8]设计了融合Powell搜索法的遗传算法,有效加强了遗传算法的局部搜索能力;张于贤等[9]针对蚁群算法收敛速度慢且易陷入局部最优解的问题,加入了基于生物记忆曲线原理的信息素更新规则,验证了改进算法的优势;刘洪铭等[10]为了避免粒子群算法易早熟的问题,利用自适应权重和混沌方法改进了粒子群算法,提高了粒子的利用率,平衡了全局和局部搜索能力;赵敏等[11]为了改善人工鱼群算法在搜索后期盲目性大、精度低等问题,加入了步长参数分解和柔性参数设置等策略,并在算法后期加强了局部搜索能力。此外,还有其他改进遗传算法[12-14]、改进蚁群算法[15,16]、改进粒子群算法[17-19]、改进鱼群算法[20]等。
综上所述,经典智能算法的研究和应用已趋于成熟,性能提升难。同时,在处理大规模的组合优化问题时,传统算法具有明显局限性,难以获得满意的求解精度和速度;而新型群智能优化算法融合了群体优化方法和数据挖掘方法,在求解复杂问题时表现出较大优势,是智能算法未来的发展趋势[21],对其进行探索研究具有更大的意义。
鉴于此,本研究以完工时间和机器总能耗作为优化指标,综合考虑机器调整环节的完工时间和总能耗,建立带有调整时间的绿色车间调度模型,运用加权归一方式对两个指标的量纲进行统一,依据指标的赋值特点,将生产分为3种不同的模式;采用头脑风暴优化算法对绿色调度模型进行求解;算法融合群体智能优化方法和数据挖掘策略,可实现满意解的快速收敛。
1 绿色柔性作业车间调度模型
1.1 问题描述
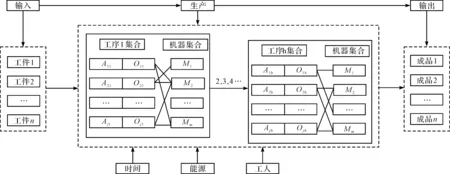
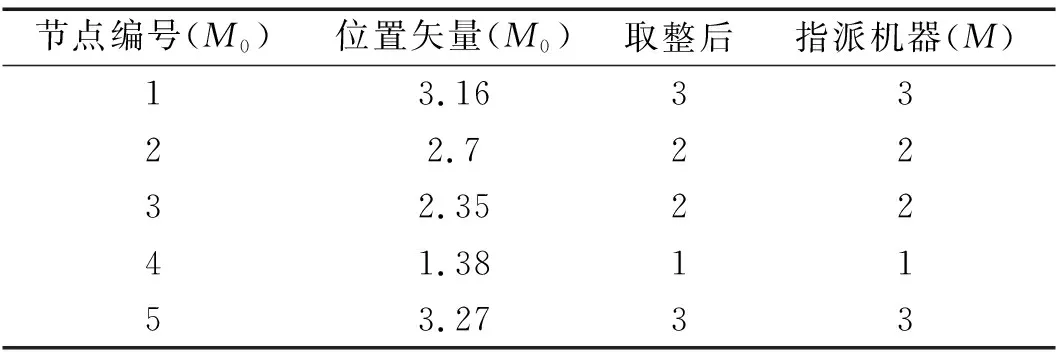
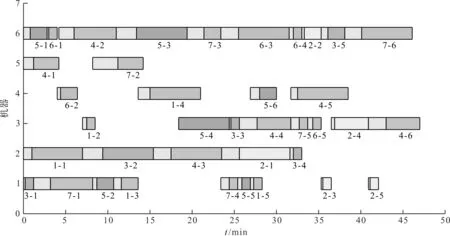
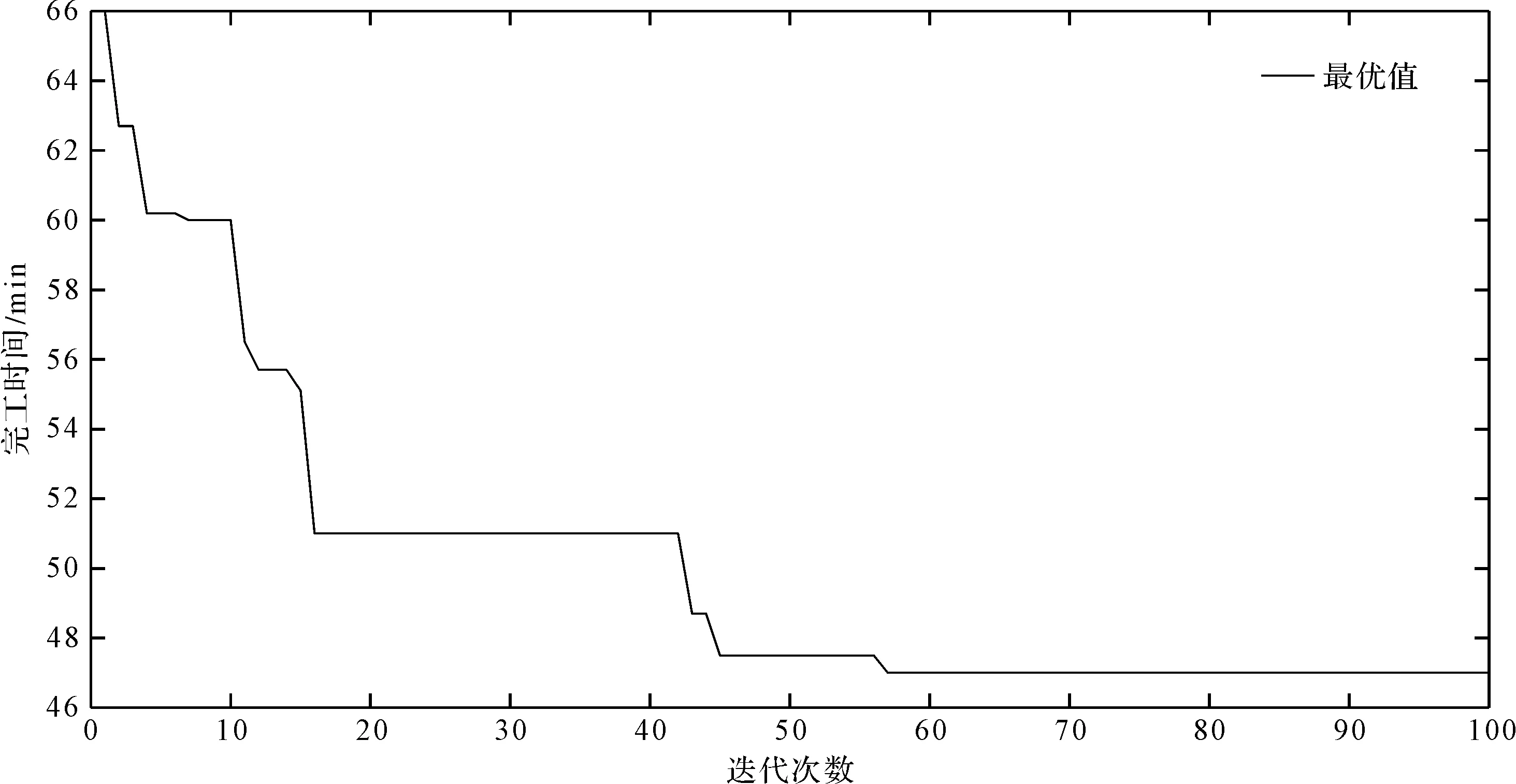
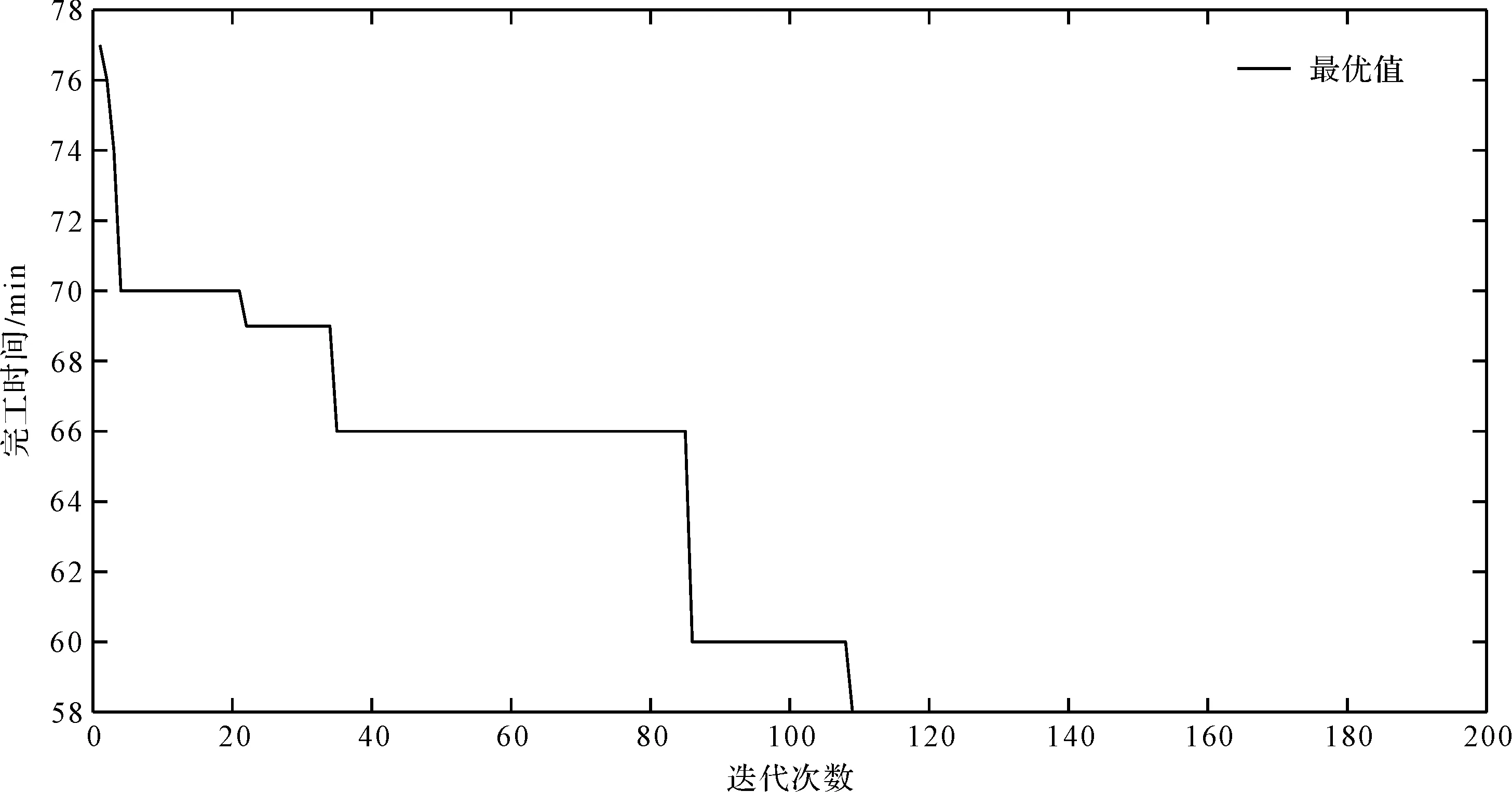
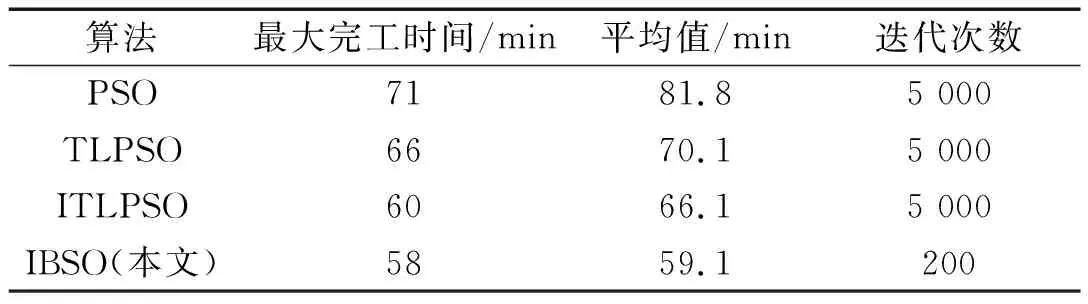
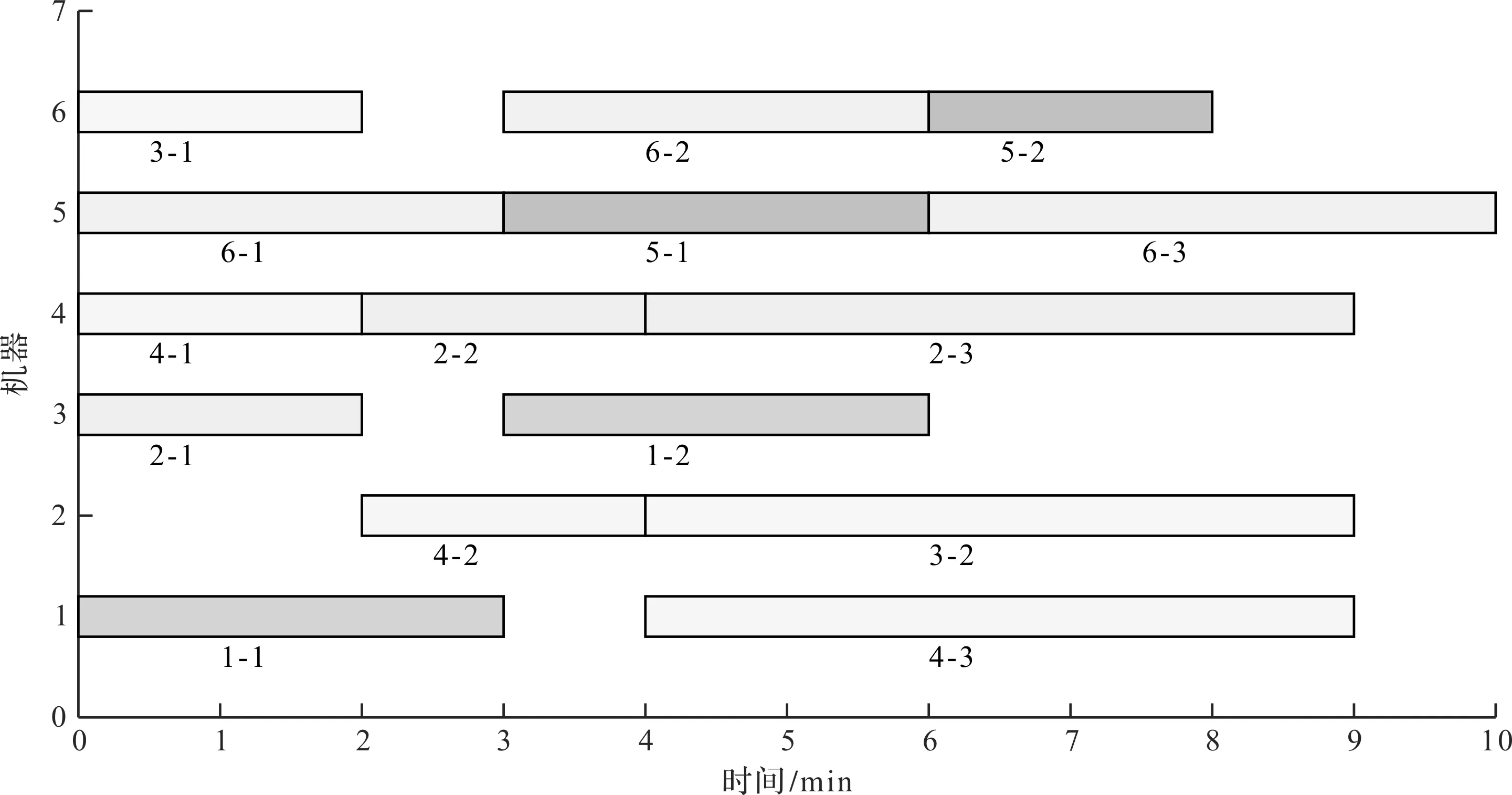
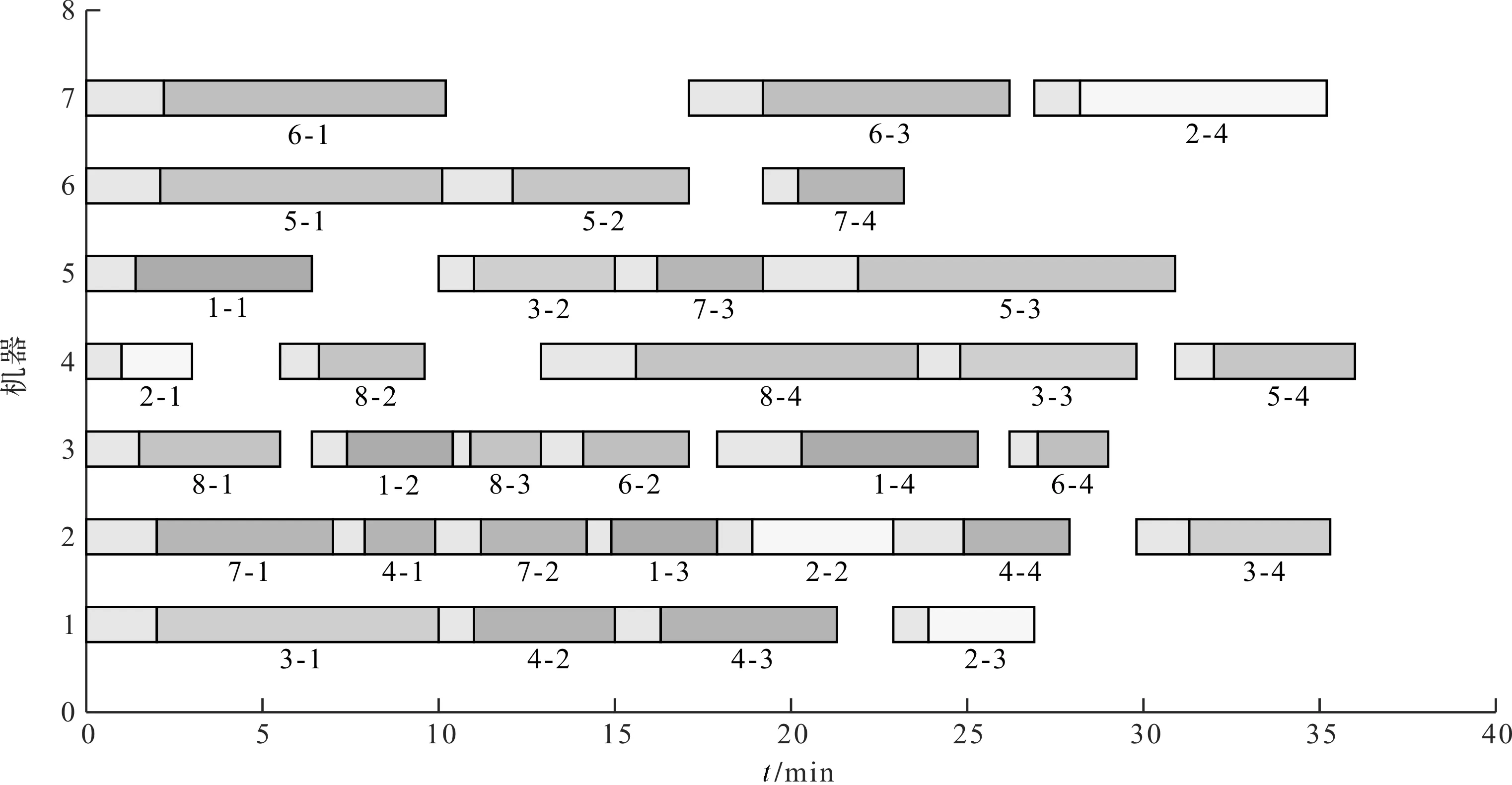
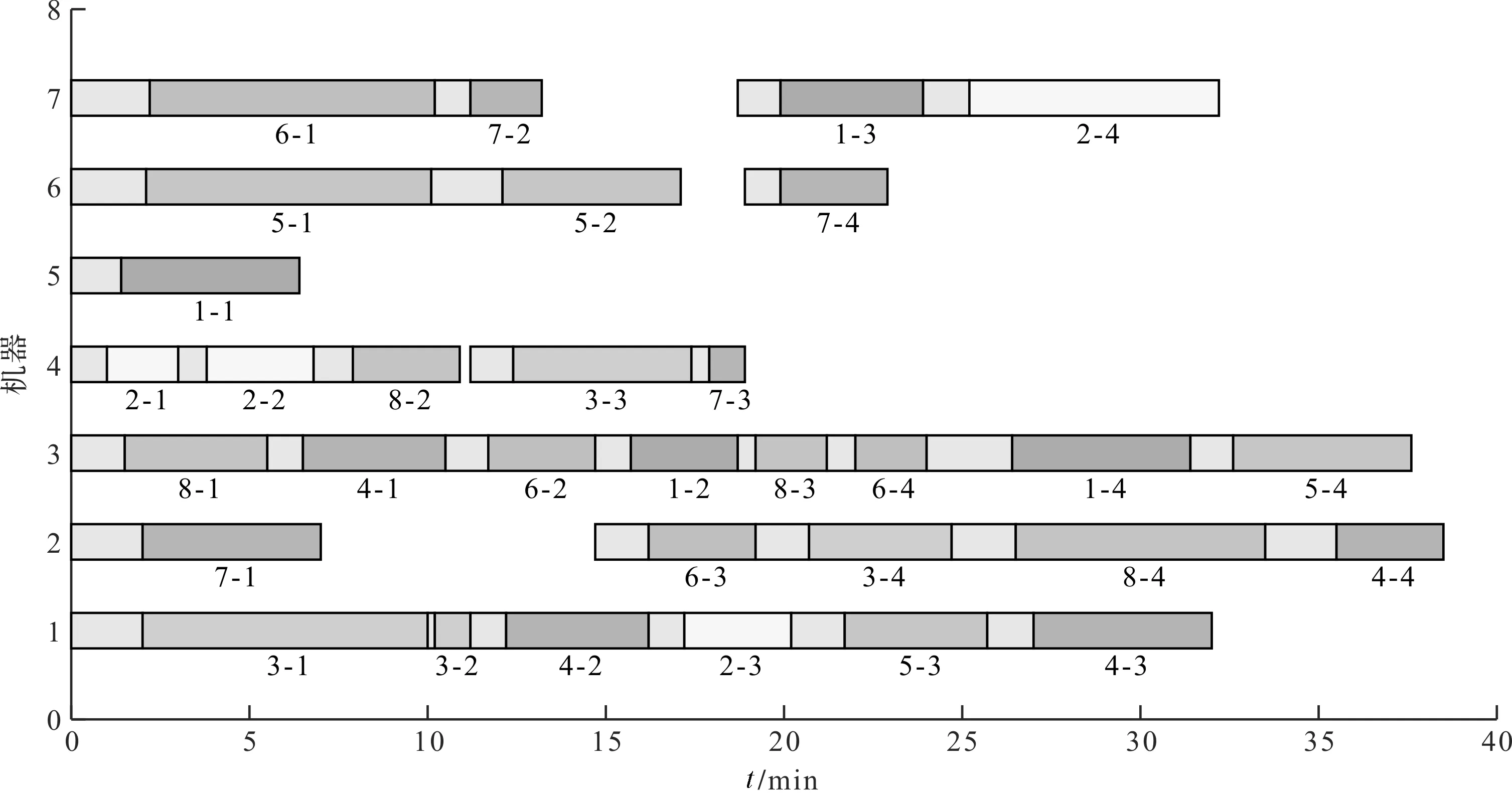
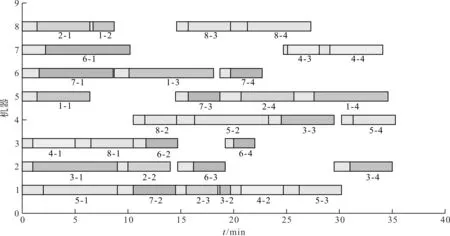
考虑调整时间的绿色柔性作业车间调度问题(以下简称GFJSP)描述如下:n个工件在m台机器上加工,每个工件有多道加工工序,所有工序在加工前均需进行调整操作;调整操作和加工操作之间没有等待时间,且调整操作只能在加工操作之前;只考虑机器加工的柔性,不考虑工件工序的柔性,即工件的工序顺序是确定的;工件的加工时间和调整时间的长度取决于所选机器的加工特点和性能。工件n的第h道工序的Ojh具有可选择的机器数mjh(mjh 绿色调度就是在满足工艺加工的前提下,通过为每个工件分配高效或节能的加工机器、确定不同工序间的最佳排序,达到绿色环保、按期交货的优化目标。 为了便于理解,笔者给出2个工件在3台机器上加工的简单实例。 2×3 GFJSP问题加工和调整时间表如表1所示。 表1 2×3 GFJSP问题加工和调整时间表 表1可以描述为2个工件在3台机器上进行加工,调整时间和加工时间用“/”隔开,“-”表示该工序不能用上面的机器进行加工,其他工序均可。 柔性作业车间生产流程图如图1所示。 图1 柔性作业车间生产流程图O—加工时间;A—调整时间;连线—工序可用的加工机器 从生产效率和生态环境的角度出发,调度指标选取最大完工时间和机床总能耗。 (1)最小化最大完工时间。缩短工件的生产周期,保障企业能够准时交货,是调度研究中最根本的优化指标。 Cmax=min(max(Cj)) (1) 式中:Cmax—最大完工时间;Cj—工件的完工时间;n—工件总数;j—机器序列,j=1,2,3…n。 (2)最小化总能耗。主要的节能减排方式,企业降低成本、保护环境。 E=E1+E2 (2) 式中:E—机床总能耗;E1—机床加工状态的能耗和;E2—机床空转状态的能耗和。 E1=∑mYm1∑i,jxijh×Pijh (3) 式中:xijh—0-1变量;Ym1—机器加工功率;m—机器总数;Pijh—第j个工件的第h道工序在机器i上加工时间。 其中:xijh是0-1变量,如果工序Ojh选择机器i,xijh值为1,否则为0;i=1,2,3…m。 (4) 式中:xijh—0-1变量;Ym2—机器空转功率;Cjh—第j个工件的第h道工序加工完成时间。 将式(3,4)代入式(2)得: (5) 绿色调度模型受到的约束如下: Cjh-Sjh=Vijh+Pijh (6) 式中:Sjh—第j个工件的第h道工序调整开始时间;Vijh—第j个工件的第h道工序在机器i上调整时间。 Sjh+Vijh≤Hjh (7) 式中:Hjh—第j个工件的第h道工序加工开始时间。 Sjh+xijh×(Vijh+Pijh)≤Cjh (8) 式中:Cjh—第j个工件的第h道工序加工完成时间。 Cjh≤Sj(h+1) (9) 式中:Sj(h+1)—第j个工件的第h+1道工序调整开始时间。 Cjhj≤Cmax (10) 式中:Cjhj—所有工件的完工时间。 Sjh+Vijh+Pijh≤Skl+L(1-yijhkl) (11) 式中:L—工序序号;yijhkl—0-1变量。 其中:yijhkl是0-1变量,如果工序Oijh先于Oikl加工,yijhkl值为1,否则为0;L=1,2,3…hj。 Cjh≤Sj(h+1)+L(1-yiklj(h+1)) (12) 式中:yiklj(h+1)—0-1变量,k=1,2,3…n。 (13) 式中:mjh—第j个工件的第h道工序的可选加工机器数;xijh—0-1变量。 (14) 式中:hj—第j个工件的工序总数;xikl—0-1变量。 (15) 式中:hk—第k个工件的工序总数;xijh—0-1变量。 Sjh≥0,Cjh≥0 (16) 式中:Sjh—第j个工件的第h道工序调整开始时间;Cjh—第j个工件的第h道工序加工完成时间。 式(6)表示工序的加工时间和调整时间之间没有间隔时间;式(7)表示工序的调整时间在加工时间之前;式(8,9)属于工件约束,表示每个工件的工序的先后顺序约束;式(10)表示所有工件的完工时间不能超过最大完工时间;式(11,12)表示同一时刻同台机器只能加工一道工序;式(13)表示同一时刻同一道工序能且只能被一台机器加工;式(14,15)表示每台机器存在循环操作;式(16)表示每个参数变量均为正数。 为了便于决策者调整能耗和时间的目标权重以适应不断变化的环境,笔者采用归一法消除不同目标之间的量纲,再用加权法将多个目标合并,处理后的目标函数表达式如下: (17) 式中:α—完工时间权值;β—能耗权值;Cmax—最大化完工时间值;Cmin—最小化完工时间值;C—当前完工时间值;Emax—最大能耗值;Emin—最小能耗值;E—当前能耗值。 其中:α+β=1。 史玉回教授[22]2011年提出了头脑风暴优化算法。算法的核心思想是:不断在他人方案的基础上提出新方案,对比后保留较好方案,并重复这一过程,最终得到最佳方案。 2.1.1BSO的编码方案 改进BSO算法的单一编码方式为多层编码方式。相较于单层编码方式,多层编码方式更能准确表达解。编码分为两层,分别是工序层和机器层,用集合S、M表示。为了便于理解,给出1个具体的编码实例:{34125/32213},工序层S={3,4,1,2,5},机器层M={3,2,2,1,3}。 工序层中的数字代表工件,工件编号出现的次数对应该工件的第几道工序,表中所有工件编号都只出现了1次,所以都是相应工件的第1道工序。 (1)工序层编码方案 工序层编码是1个集合S。初始得到随机排序集合S0的位置矢量,依据位置矢量大小重排后,得到优化后工序优先度排序S。个体位置矢量向工序排序转换如表2所示。 表2 个体位置矢量向工序排序转换 由表2可知:解码后的工序优先度为O31→O41→O11→O21→O51。 (2)机器层编码方案 机器层编码为工序指派机器的集合M,其基因是工序所选择的可用机器。首先,初始得到随机指派集合M0的位置矢量,若位置矢量不是整数,则属于无效编码。当出现无效编码时,对位置矢量的大小向下取整,得到工序要指派的机器集合M。 个体位置矢量向指派机器转换如表3所示。 表3 个体位置矢量向指派机器转换 最后,将编码S和M组合在一起,代表优化后的1个可行解:{3412532213}。为了避免第1层(工序)基因对应的第2层(机床)基因超出工序可用机床范围,即产生非法染色体,第2层编码对应指派工序的机器为该工序的“第几个”可用机器,而不是全部机器,有效避免了非法染色体的产生。 2.1.2BSO的解码方案 (1)编码意义。以上实例中的决策编码G={3,4,1,2,5/3,2,2,1,3},工序解码得到U={3,4,1,2,5/3,2,2,1,3},拆分后得到工序编码S={3,4,1,2,5}和机器编码M={3,2,2,1,3}。 S={3,4,1,2,5}表示的意义为:第1位的3表示工件3的第1个工序;第2位的4表示工件4的第1个工序;第3位的1表示工件1的第1个工序;第4位的2表示工件2的第1个工序;第5位的5表示工件5的第1个工序。 M={3,2,2,1,3}表示的意义为:第1位的3表示工件3的第1个工序用它的第3个可用机器加工;第2位的2表示工件4的第1个工序用它的第2个可用机器加工;第3位的2表示工件1的第1个工序用它的第2个可用机器加工;第4位的1表示工件2的第1个工序用它的第1个可用机器加工;第5位的3表示工件5的第1个工序用它的第3个可用机器加工。 (2)解码过程。从S的第1个编号开始,第1位的3表示工件3的第1个工序被先加工,然后根据机器编码找到其工序对应的是第3个可用机器。其全部可用机器集合为{2,3,5},故第3个可用机器是机器5,即在机器5上开始加工,得到开始时刻和结束时刻。 依次可知S的第2个编号,代表工件2的第1个工序。工件2的第1个工序对应机器集合为{4,5,6},根据机器编码,它的加工机器是第2个可用机器,也即5号机器,则5号机器要等前1道工序加工完成后才能开始加工本工序,即本工序开始加工时刻等于5号机器上1个工序完成的时刻;以此类推完成整个调度。 BSO的聚类算子是决定优化效果的关键因素,作用是将相似个体归为同组。采用k-means聚类算法,以N个数据点作为输入,把点的相似度作为分类标准,将N个点归类到不同组别。通过k-means操作,不断把更好的解挑选出来,最后将挑选后的所有解聚集在一个较小的解空间里。pclustering是随机解替换聚类中心的概率参数,能够避免算法早熟收敛,帮助算法跳出局部最优解。 其具体的实现步骤如下: (1)聚类操作将n个解分为m个簇; (2)确定簇心计算每个簇中所有个体的适应度值,将最优个体作为簇心; (3)设置数值设定值pclustering,随机生成rclustering值,p、r∈[0,1); (4)替换簇心当r BSO的分类算子对结果的影响也很重要,其作用是基于旧解来产生新解。分类操作采用高斯变异方式,即: (18) 其中:w1+w2+…wn=1。 (19) 式中:T—最大迭代数;t—当前迭代数;k—控制搜索步长的调整系数,作用是平衡算法的收敛速度;rand()—随机函数,rand()∈[0,1)。 其具体的实现步骤如下: (1)确定rgeneration。生成一个区间在[0,1)的随机数rgeneration; (2)比较rgeneration和pgeneration大小。pgeneration为预先设定好的参数值; (3)若rgeneration (4)若rgeneration>pgeneration,则随机选择2个簇,步骤可类比(3); (5)通过设定参数来保持上述4种方式产生的新个体的比例在新个体产生后,与旧个体进行比较,较优的个体将会被保留并作为新一代中的个体。 绿色车间调度要同时优化完工时间和能耗指标,适应度函数选式(17)。式中,α、β分别为完工时间和能耗的权重,指标权重越高代表重要程度越高,在同等条件下,迭代优化时会优先处理权重高的指标。 新解选择保证了种群的多样性,操作是基于数据分析的保留策略将适应度更高的新解替换旧解,将个体逐一进行更新,直到达到最大更新代数。 头脑风暴算法流程图如图2所示。 图2 头脑风暴算法流程图 2.6.1 实验1 为了测试IBSO算法的性能,实验1选取较为相近的标杆文献[23]算例进行测试。算例为10×6的实际生产数据,以最小化最大完工时间为优化指标,终止条件为最大迭代代数到达100代,算法参数设置与文献相同。考虑调整时间的甘特图如图3所示。 由图3可知:IBSO算法的最大完工时间为47 min,而文献中IGA的最优解为55 min,最大完工时间缩短了8 min,效率提升14.5%。 图3 考虑调整时间的甘特图 考虑调整时间的收敛曲线如图4所示。 图4 考虑调整时间的收敛曲线 由图4可知:IBSO的初始解66 min与IGA的初始解70 min基本相同;约经过10代的迭代之后,IBSO的解稳定在51 min左右,而IGA的解稳定在58 min左右,此时BSO的解已经优于IGA算法迭代终止的最优解;在迭代次数达到60代后,IBSO已经找到了最优解47 min,IGA则在90代之后找到了最优解55 min。IBSO在开始阶段就快速收敛,之后收敛速度逐渐降低,验证了IBSO的初始解集的质量较高,具有良好的全局搜索能力。 测试结果表明,IBSO算法优于IGA算法。 2.6.2 实验2 实验2的8×6的工件测试数据来自文献[24],由6个工件、8台机器、26道工序组成。为了测试IBSO算法性能,目标函数选取最小化最大完工时间,算法初始参数设置相同。 实验2收敛曲线图如图5所示。 图5 实验2收敛曲线 由图5可知:IBSO算法的最优解为58 min。IBSO算法迭代到约80代时,已达到TLPSO 算法的最优值60 min,再经过30代迭代,达到最优值58 min,并一直稳定于该值。测试文献中,普通粒子群算法(PSO)、双层粒子群算法(TLPSO)、改进的双层粒子群算法(ITLPSO)的最优解分别为71 min、66 min、60 min,IBSO求解的最大完工时间均有所减少,尤其比PSO算法降低了13 min。 4种算法的最大完工时间及迭代次数如表4所示。 表4 对比4种算法的最大完工时间及迭代次数 由表4可知:IBSO算法在收敛速度和精度方面均优于实验2文献的3种算法。 2.6.3 实验3 实验3的6×6工件测试数据来自文献[25],包含6个工件、6台机器和15道工序。算法的目标函数和参数设置与文献一致。 实验3调度甘特图如图6所示。 图6 实验3调度甘特图 由图6可知:IBSO算法的最优解为10。文献中CE-MOFJSP算法的最优解为11 min,最大完工时间缩短了1 min。IBSO算法迭代到70代时已达到CE-MOFJSP的最优解11 min,到80代时达到最优解10 min,而CE-MOFJSP算法在100代到达最优解11 min,收敛速度略快于文献算法。 对比2种算法帕累托最优解和平均值如表5所示。 表5 对比2种算法的帕累托最优解 由表5可知:IBSO算法对应的帕累托解集均优于CE-MOFJSP,帕累托解平均值减少1.67 min,优化效率平均提高13.9%。该结果表明:IBSO算法优于CE-MOFJSP算法。 某制造企业的零件加工车间属于典型的柔性作业车间,每个工件在机床上加工时,都需要进行安装、定位、对刀或测量等调整操作,调整时间的长短由机床特性和工人熟练程度决定。在保证质量和工艺的前提下,笔者通过制定适宜的调度方案来尽可能降低最大完工时间和机床总能耗。 仿真平台选取MATLAB2018a,运行环境及配置为Intel Corei5-4210 2.6 GHz CPU、4.00 RAM、Windows 10 64位操作系统。参数设置为:最大迭代数为500;种群大小为50;选择一个簇形成新个体的可能性Pclustering=0.8;选择一个簇中心以替换为随机生成的中心的概率Pgenetation=0.2。优化结果如表5所示。 实例中有8个工件,8台机器。车间工件能耗与时间信息如表6所示。 表6 车间工件能耗与时间信息 为了说明数据的含义,笔者以表中工件1的第1道工序为例:工件J1的工序O11选择M1加工时,加工时间为4 min,调整时间为1.5 min,加工功率为1 278 W,空转功率为370 W,所有工件所有工序均依次类推即可。 笔者将指标间的权重系数组合分为10组,每组均在MATLAB环境下运算20次,再求出完工时间和能耗的平均值。 3种模式下的实验结果如表7所示。 表7 3种模式下的实验结果 由表7可知:根据指标权重的赋值特点,可将生产分为3种典型模式:绿色模式、综合模式、高效模式。从表中可以看出,完工时间和能耗两个指标在优化过程中的关系是相互冲突的,无法同时得到两者的最优解,只能通过调整指标权重得到一组pareto最优解。整体来看,机器空转能耗较高,总空转能耗占总加工能能耗的21.36%;结合典型指标来看,当α=0,β=1时,最大完工时间为41.7 min,总能耗为156 252 J;当时,最大完工时间为34.2 min,总能耗为216 265 J。 两种方案在生产效率和绿色环保方面表现出的优劣势较为明显,因此企业应结合具体面临的生产情境,确定相应的生产模式,得到更有针对性的调度方案。笔者从3种模式中各选取1个代表方案,进行对比研究。 (1)综合模式。企业在生产过程中,既有生产效率的压力,又有绿色环保的规制,该情境适合采取综合模式。取α=0.5,β=0.5时,最大完工时间为36 min,总能耗为176 719 J。 综合模式下的甘特图如图7所示。 图7 综合模式下的甘特图 由图7可知:由于完工时间指标和能耗指标的权重相同,加工时间和加工能耗差异不大的机器所表现出的适应度值基本相同,故工件可选择的机器数增加,工件在机床上的分布也较为均匀。机器8因为设备老化、维保不足等问题,各道工序加工能耗较高。由于能耗指标的限制,机器8未被安排加工任务。 (2)绿色模式。企业在面临严格的环保规划,或者客户对订单的交货期要求比较宽松的情况下,可以采取绿色环保的生产模式,将能耗水平降至最低。取α=0.2、β=0.8时,最大完工时间为38.5 min,总能耗为156 670 J。 绿色模式下的甘特图如图8所示。 由图8可知:机器3加工负荷最大。通过查找表6的工件能耗信息可知,机器3在加工O62、O12、O54工序时,相比所有可用机器,消耗的能量是最低的;在加工O41、O14工序时,也较为节能。多道工序在绿色模式下流向机器2,造成机器2的高负荷。同理,指派机器1加工O31、O23、O43工序,以及工序O71、O34在机器2上加工,都是最佳的节能机器匹配。机器8节能属性较差,在该模式下不安排加工任务。 图8 绿色模式下的甘特图 (3)高效模式。当企业的生产订单对时间因素较为敏感和严格的情况下,决策者可以采取高效生产模式。取α=0.8、β=0.2时,最大完工时间为35.3 min,总能耗为193 707 J。 高效模式下的甘特图如图9所示。 图9 高效模式下的甘特图 由图9可知:在高效模式下,为了保证生产速度,工件主要选择那些加工速度快的机器,并不注重加工能耗的高低,故能耗高的机器和能耗低的机器同时开始运行,使得工件的分布最为均匀。此时,机器8承担了4道加工工序。相比与所有可用机器,机器8加工O12和O84时速度最快,加工O12和O84时速度次最快。 以往的绿色车间调度文献没有考虑机床调整时间及其能耗,导致调度方案和实际差别较大。针对这一不足,本文构建了带有调整时间的绿色车间调度模型,在模型中综合考虑了设备的调整和加工环节所产生的时间和能耗,并依据指标权重的特点将生产模式划分为3类,使调度方案更加科学有效;在单层编码头脑风暴算法的基础上,设计了多层编码头脑风暴优化算法,在搜索操作中应用群智能优化方法和数据挖掘策略,提高了求解的精度和速度;通过对标杆算例和生产实例进行仿真,验证了本研究的模型和算法的有效性,实现了绿色车间调度。 针对未来的研究,笔者还会将车间生产的运输环节和机器故障环节等多个生产过程进行集成后建模,融合其他智能算法,采用混合头脑风暴算法进行求解,使绿色车间调度更完善、更高效。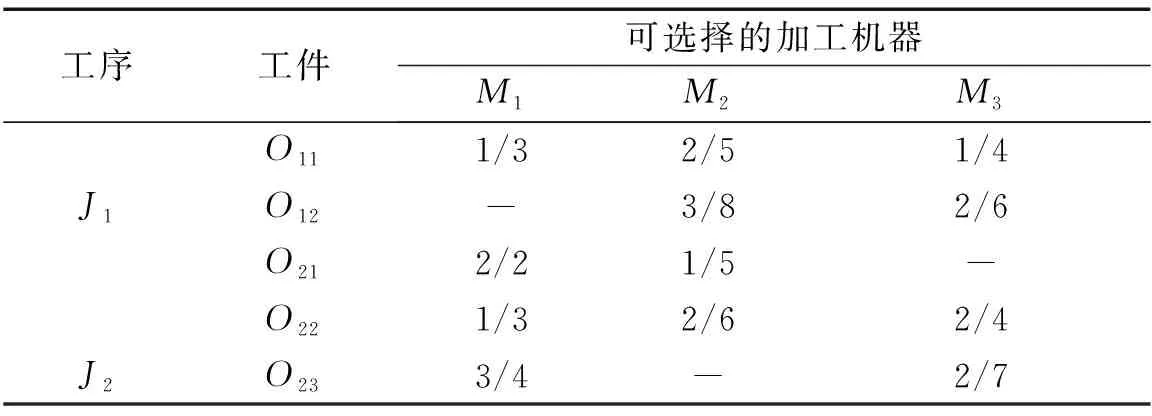
1.2 考虑调整时间的绿色调度模型
2 头脑风暴优化算法
2.1 BSO编码与解码

2.2 BSO解的聚类
2.3 BSO解的分类

2.4 适应度值
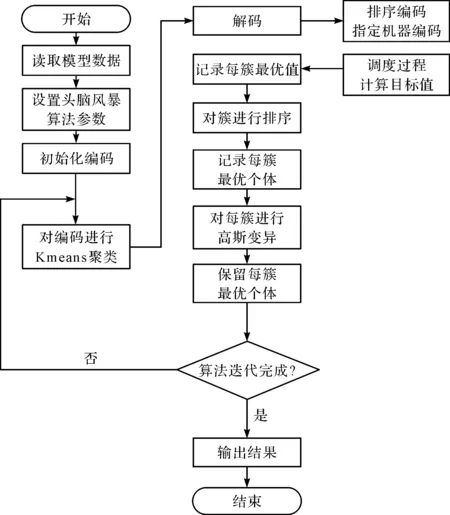
2.5 BSO新解选择及算法流程图
2.6 性能测试

3 实验与结果分析


4 结束语

