混凝土水化放热模型的实验分析和计算

李 东， 张晔琛

(上海大学土木工程系， 上海 200444)

很多大体积混凝土工程中出现的表面裂缝和结构裂缝， 都是由混凝土水化反应中的热量聚集、温度升高造成的.混凝土开裂会严重影响结构的耐久性和正常使用， 因此有必要对大体积混凝土结构的温度场进行准确预测[1-2].在大体积混凝土温度应力场分析中， 胶凝材料水化是一个重要因素， 而混凝土放热模型是探究混凝土水化反应的重要参数.因此， 根据实验资料来建立考虑各种因素影响的混凝土放热模型尤为重要.混凝土放热模型的精确与否会直接影响混凝土温度应力场计算结果的精度.

已有研究对大量的水化热及水化温升实验资料进行了分析， 归纳总结了多种水化放热模型.美国垦务局依托大量实验数据， 得到了指数式水化热模型[3].蔡正咏[4]提出了双曲线式水化热模型.朱伯芳[5-6]在指数式水化热模型的基础上， 推导了复合指数式模型; 后续又在复合指数式模型的基础上增加了温度对水化热的影响因子.大部分放热模型只考虑了龄期、温度对水化反应的影响.然而， 为了改善混凝土的性能及节约原料， 很多工程都需要用到矿物掺合料， 其中粉煤灰在胶凝材料的水化过程中具有物理化学效应， 对水泥水化反应具有不可忽略的影响.因此， 已有的混凝土放热模型仍有待完善.

本研究依托水泥水化动力学原理及不同矿物组成的水泥水化热实验数据， 通过数据拟合计算， 提出了较为简单的、考虑了粉煤灰掺入的混凝土水化放热模型， 提高了计算结果的精度.

1 混凝土水化放热模型的修正

基于水化度的概念， 水泥水化反应速率为

式中:r为水化反应速率;αc为水泥水化度;Q(t)为龄期t时的水化热(kJ/kg);Q0为水泥完全水化的水化热， 一般工程中取28 d 时的水化热(kJ/kg).

根据化学反应动力学原理， 等温条件下均相反应的动力学方程[7]为

式中:c为浓度;f(c)为反应机理函数;k(Tj)为反应速率常数.在化学反应过程中， 可以用Arrhenius 方程[8]表示温度对反应速率的影响， 即

式中:k0为常数;Tj为热力学温度(K);E为化学活化能(J/mol);R为气体常数， 一般取8.314 J/(K·mol).通常情况下，取恒定值2 700 K.

在非均相体系水泥中， 使用反应物向产物的转化度， 即水化度αc来替代浓度c， 即

根据水泥水化机理可知， 随着t的增加， 水化度的函数值单调递增.由式(4)可得

式中:αc(t)为龄期t时的水化度， 当t →∞时，αc→1;a，b为与胶凝材料组成有关的影响系数;k为考虑了温度对水化反应速率影响的系数， 在恒温条件下为常数.

将式(5)代入式(1)可得水化热表达式:

2 粉煤灰对水化热的影响

文献[9]对粉煤灰掺量分别为0%， 30%， 40%， 50%， 60%， 70% 的6 组水泥进行了水化热实验.通过式(6)对6 组实验数据进行了拟合， 结果如图1 所示.

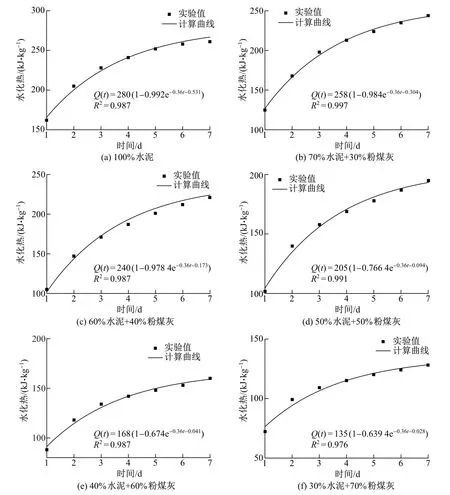
图1 不同粉煤灰掺量的水化热实验与修正公式曲线Fig.1 Experiments data and correction formula curves of different fly ash mixed with heat of hydration

由图1 可知， 6 组实验的计算值与实验值均较为吻合， 相关系数R2均接近于1， 具有较好的拟合精度， 可以满足工程计算的要求.随着粉煤灰掺量的增加， 复合胶凝材料的水化放热量明显减少.原因是粉煤灰对水泥水化反应具有稀释效应、化学效应及物理效应; 相同质量的粉煤灰相比水泥水化反应放热量少.

当粉煤灰掺量分别为0%， 30%， 40%， 50%， 60%， 70%时， 式(6)中28 d 时水泥水化热Q0的拟合值分别为280， 258， 240， 205， 168， 135 kJ/kg; 与胶凝材料组成有关的影响系数a的拟合值分别为0.992， 0.984， 0.978， 0.766， 0.674， 0.639， 影响系数b的拟合值分别为0.531， 0.304，0.173， 0.094， 0.041， 0.028.由此可知: ①28 d 时水泥水化热大致随着粉煤灰掺量的增加而减小， 但并非成固定比例减小; ②影响系数a大致随着粉煤灰掺量的增加而减小; 当粉煤灰掺量小于40%时， 影响系数a相差不大， 平均在0.98 左右; 当粉煤灰掺量大于40%时， 影响系数a明显减小， 相比粉煤灰掺量40%时， 大致减小19.6%～34.6%， 说明此时粉煤灰对水化速率的影响较大， 可有效降低胶凝材料的水化热; ③影响系数b大致随着粉煤灰掺量的增加而减小， 但并不成线性变化， 说明粉煤灰的掺入对胶凝材料水化反应具有不同的影响效应.

根据实验规律， 可求得水化热Q0、影响系数a，b与粉煤灰掺量的关系， 即

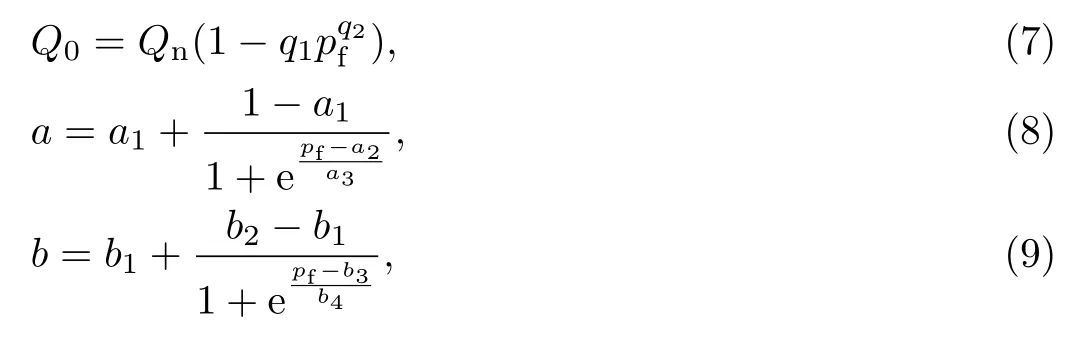
式中:pf为胶凝材料中粉煤灰的质量分数(%);Qn为100%水泥28 d 时的水化热(kJ/kg);q1，q2，a1，a2，a3，b1，b2，b3，b4为材料常数.

3 混凝土绝热温升

3.1 基于等效龄期的绝热温升表达式

根据等效龄期概念[10]， 可以用等效龄期te来表示温度对水化反应速率的影响， 即

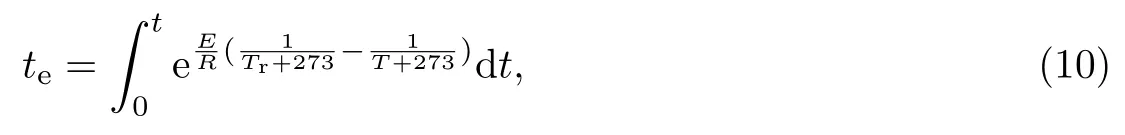
式中:Tr为混凝土参考温度;T为混凝土温度，T=T0+θ， 其中T0为初始温度，θ为混凝土绝热温升.

由式(3)可得， 当温度分别为T1和T2时， 胶凝材料水化反应速率的比值为

令T2=293 K， 可得到其他温度的反应速率常数与293 K(20°C)时的比值:

将式(12)和(10)代入式(6)， 可得

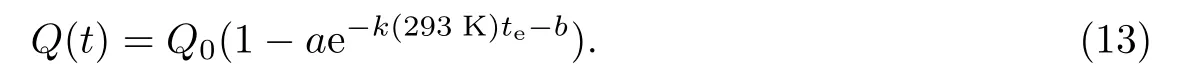
在绝热条件下， 混凝土中水泥水化反应放出的热量会全部转化为温升， 即

将式(13)代入式(14)， 可得基于等效龄期的绝热温升计算模型， 即

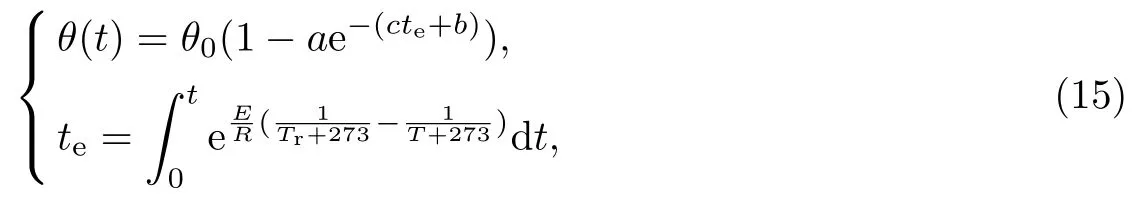
式中:θ0为最终绝热温升值， 与混凝土胶凝材料的用量、组成有关.θ0可表示为

式中:M为单位体积胶凝材料的用量(kg);C为混凝土比热容(kJ/(kg·°C));ρ为混凝土密度(kg/m3).

本研究基于化学反应动力学原理及热力学理论推导的绝热温升计算模型(15)， 适用于在绝热条件下的任何混凝土水化反应温升过程， 并且可利用等效龄期描述温升对水化速率的影响.

3.2 绝热温升实验算例

本研究选取文献[11]中不同温度下混凝土绝热温升的实验数据， 如表1 所示.根据非线性最小二乘法计算原理对式(15)以及复合指数式模型θ(t)=θ0(1-emtn)[5]的参数进行拟合， 拟合结果如图2 和3， 表2 和3 所示.

表1 绝热温升实验数据Table 1 Adiabatic temperature rise experimental data °C

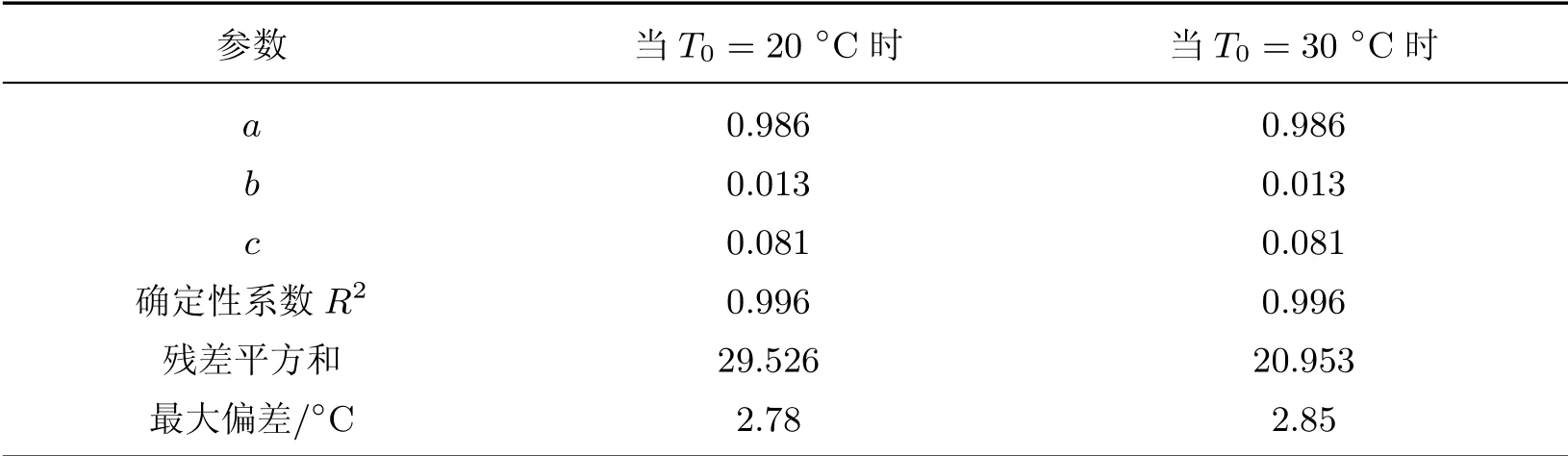
表2 式(15)的参数、各组误差及相关系数Table 2 Parameters and each group of errors and related parameters of Formula (15)

图2 式(15)的模拟值与实验值对比Fig.2 Comparisons of experimental values and simulation values of Formula (15)

图3 复合指数式模型的模拟值与实验值对比Fig.3 Comparisons of the experimental values and the simulation values of the compound exponential model

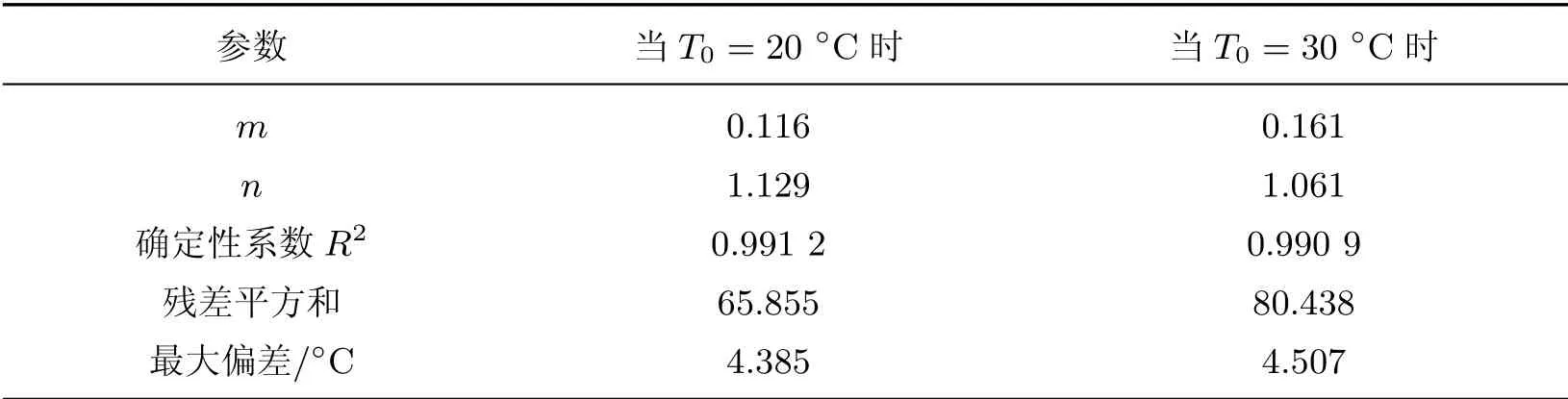
表3 复合指数式模型的参数、各组误差及相关系数Table 3 Parameters and each group of errors and related parameters of the compound exponential mode

由图2 和3 可知: 在不同浇筑温度下， 模拟值和实验值随龄期、温度的变化规律和增长幅度基本保持一致; 式(15)的模拟值和实验值更为吻合， 误差较小， 尤其在7 d 以前， 吻合情况明显好于复合指数式模型.由表2 和3 可知: 式(15)的拟合误差较复合指数式模型有所减小， 确定性系数有所提高， 最大偏差降低了2°C 左右.这说明基于等效龄期的绝热温升表达式合理有效， 并且可以更准确地描述不同温度下混凝土的绝热温升过程.

4 结 论

(1) 由于计算难度的限制， 已有的大部分混凝土水化放热模型并未考虑粉煤灰掺入、温度等的影响.本研究依托水泥水化动力学原理及不同矿物组成的水泥水化热实验数据， 通过数据拟合计算， 提出了较为简单的、考虑了粉煤灰掺入的混凝土水化反应放热模型.该模型可以准确反映混凝土水化反应放热量及温升随龄期的变化， 为此类问题的解决提供了新思路.

(2) 利用不同粉煤灰掺量的水泥水化热实验数据对本研究修正的放热模型进行拟合.结果表明: 影响系数a大致随着粉煤灰掺量的增加而减小; 当粉煤灰掺量大于40%时， 影响系数a的减小幅度明显增大， 说明此时粉煤灰对水化速率的影响较大， 可有效降低胶凝材料的水化热; 影响系数b大致随着粉煤灰掺量的增加而减小， 但并不成线性变化， 说明粉煤灰的掺入对胶凝材料水化反应具有不同的影响效应.

(3) 随着温度的升高， 混凝土的放热速率明显增大.随着粉煤灰掺量的增加， 复合胶凝材料的水化放热量明显减少， 但并不成固定比例减少.对于大体积混凝土工程， 应合理选择混凝土配比， 在强度达到要求的前提下， 适当掺入粉煤灰等混合材料， 有效降低混凝土的水化温升.