一道新教材习题的几何方法探求

广东省佛山市顺德区勒流中学(528322) 邓先春

普通高中教科书《数学》必修第一册(2019年6月第一版)【以下简称新教材】, 在内容安排上严格依据普通高中《数学课程标准》(2017年版)的课程性质与基本理念,着力落实学生的核心素养与课程目标. 这套新教材在习题的编排上关注到学生的实际,分设复习巩固、综合应用、拓广探求等三个层次,形成数学能力的递进式增长. 下面就新教材P.255第23 题用几何方法进行研究.

题目: 如图1,正方形ABCD 边长为1,P,Q 分别在边AB,DA 上的两点,当∆APQ 的周长为2 时,求∠PCQ 的大小.

图1

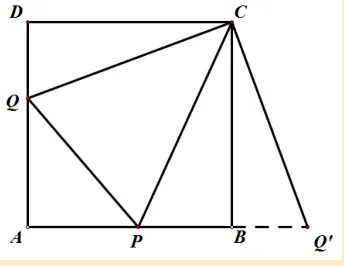
图2

此题位于新教材第五章“三角函数”内容处, 很容易联想到利用和差角的三角函数公式, 先求∠DCQ+∠BCP的三角函数值, 并由0 < ∠DCQ + ∠BCP <确定∠DCQ + ∠BCP =从而∠PCQ =(详见新教材教师用书P.293 解答,此处从略).

在新教材第215 页“两角差的余弦公式”推导过程中“把扇形OAP 绕点O 旋转β 得到重合”的启发.下面用几何方法对此进行探求解答:

因为P,Q 两点分别在边长为1 的正方形两邻边上并且满足AP +AQ+PQ = 2 = 2×1 = AB +AD, 所以PQ=2−(AP+AQ),PB+QD =(1−AP)+(1−AQ)=2−(AP+AQ),所以PQ=PB+QD. 于是将Rt∆CDQ 绕点C 按逆时针方向旋转90◦得到CD 与CB 重合,点Q 到点Q′,BQ′=DQ(如图),BQ′与AB 共线. 这样PQ′=PB+BQ′= PB+DQ = PQ,可见,在∆PCQ 与∆PCQ′中有CP = CP,CQ = CQ′,PQ = PQ′,∴∆PCQ ～= ∆PCQ′,∴∠PCQ=∠PCQ′. 又∵∠QCQ′=90◦,∴∠PCQ=45◦.

可见,用几何方法解决此类问题比用和差角的三角函数公式求解更为简单高效. 教材安排此题只不过是为了起到运用所学知识(三角知识)解决问题以达到巩固知识的作用.

于是,一般地,正方形ABCD 的边长为a,P,Q 分别为边AB,DA 上的点. 当∆APQ 的周长为2a 时, 求∠PCQ的大小. 其结果也为45◦. 证明可类似以上探究,此处从略.