五点法在正、余弦型函数含参题中的应用

广东省汕头市聿怀中学(515041) 李 虹

五点作图法就能高效的解决正、余弦型函数含参题. 它是数形结合思想方法的运用,简单实用,学生只要找到三角函数中几个关键点,就可以描绘出三角函数的简易图像,通过图像问题就能迎刃而解,且解法简捷,使复杂的三角问题简单化,抽象问题具体化,能够变抽象思维为形象思维,有助于把握数学问题的本质,它是数学的规律性与灵活性的有机结合.

1 含参单调性的问题

?

?

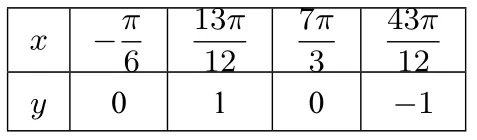
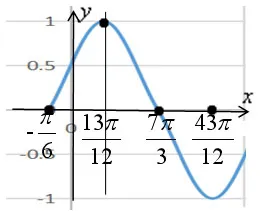
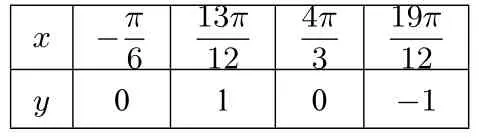
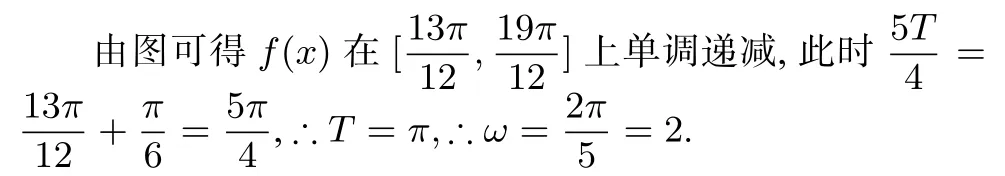
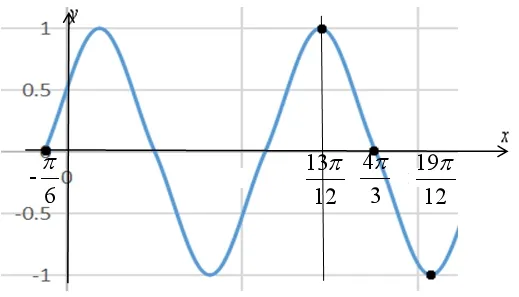
解题模板: 第一步根据题意画出第一零点,主题至少画两个周期.

解题心得: 本题在考查正弦型函数单调性,求解参数ω的问题,这类题通常是中档题或者难题,学生用三角函数的单调区间去解题会遇到较麻烦的分类讨论,学生不容易掌握该法. 用五点法画图,就会非常直观的发现它的单调性与区间的关系, 轻松比较大小, 进而求出参数的值. 我们常常以“五点法”中的第一零点作为突破口,要从图象的升降情况找准对称轴的位置,要善于抓住特殊量和特殊点. 特别指出在该类题型中,常见的参数还有A,B,ϕ,或者是动区间问题,解法与该题一样,作图会稍难.

2 含参零点的问题

例2(2019 新课标Ⅲ理12)设函数,已知f(x)在[0,2π]有且仅有5 个零点. 下述四个结论:

其中所有正确结论的编号是( ).

A. ①④ B. ②③ C. ①②③ D. ①③④

【解析】列表、画图如下:

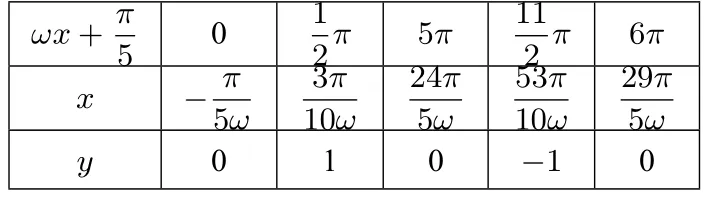
ωx+ π 5 0 1 2π 5π 11 2 π 6π x −π 5ω 3π 10ω 24π 5ω 53π 10ω 29π 5ω y 0 1 0−1 0

解题模板: 第一步要明确函数的性质与条件,然后把与试题有关的点都描出来.

第二步观察在定义域内零点的个数,我们就可以得到解答需要的等式或不等式,进而求出相关参数的范围.

第三步结合参数的范围和图像就可以解决试题中的所有答案.

解题心得: 本题是五点作图法解决正、余弦型函数含参题的典型例题. 该题虽然是“2019 新课标Ⅲ理”选择题的压轴题,但我们通过图像,能轻松得出该题的答案,相对其它方法会简单得多. 数形结合对于解多选题会有得天独厚的优势,我们可以通过一个图像观察函数的性质,可以极大的节约解题时间和提高解题准确度. 值得注意的是对于零点要从图象的升降情况判断其为“第一零点”还是“第二零点”.

3 含参正、余弦型函数值域的问题

?

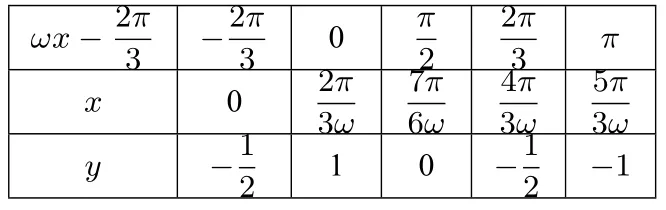
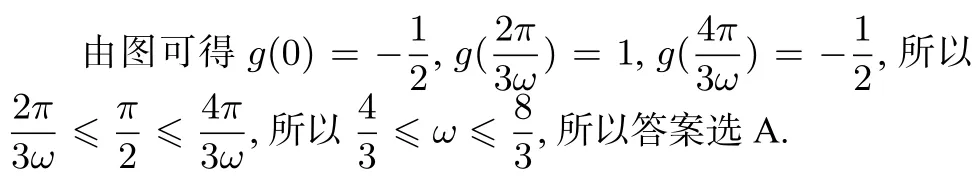
解题模板: 第一步把ωx+ϕ 看做一个整体,找出关键的五个点,列表绘制出五点图.

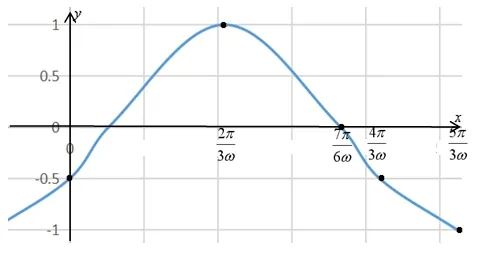
第二步注意把值域的最大值最小值标出.

解题心得:

五点作图法解决正、余弦型函数含参题,该题是非常严格地按照五点法作图求解,基本思想是把ωx+ϕ 看做一个整体,根据定义域找值域的适合区间是一类常见的题型,要从图象的升降情况找准函数的最大最小值的位置,这种题用五点法做的好处是: ①容易确定动态定义域所在位置或大致位置; ②最值点位置由图就可以得到; ③最重要的是参数可以当作常数处理会避免繁杂的讨论. 因此五点法是解这类题的不二方法.

4 含参正、余弦型函数对称轴的问题

【解析】列表画图如下:

?

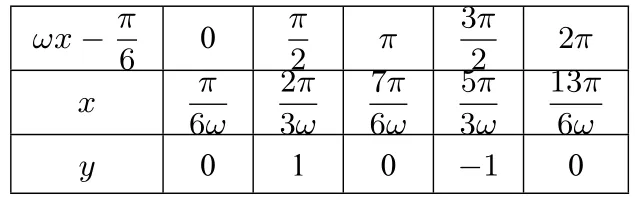
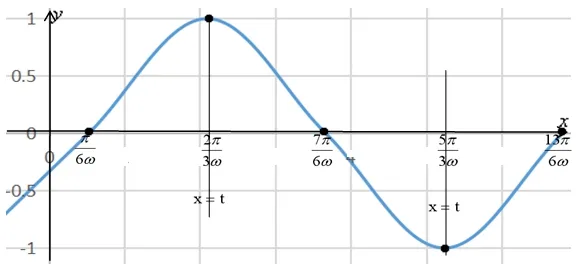
解题模板: 第一步用五点法画出一个周期的图像.

第二步在y 轴右侧画出第一条对称轴和第二条对称轴.

综上所述,“五点法”是数形结合思想的一部分,具有形象直观,易于接受等优点,且对于沟通知识间的联系,活跃课堂气氛,开阔学生思路,发展智能,提高数学水平有着独到的作用,所以,我们要高效备考高考时,一定要让学生熟练掌握“五点法”,特别是在解正、余弦型函数含参题是要优先考虑“五点法”. 该法在解其它函数题时同样很重要,在解决具体题目时可以根据需要增加或删减点的个数. 当然我们也要了解五点法的局限性,因为五点法只是大概图形,往往没办法得到精准答案.