基于MA-SVM 的家用负荷非侵入式识别

陈 飞， 杨 超， 鲁 杰

（贵州大学 电气工程学院， 贵阳 550025）

0 引 言

随着经济和科技的发展，人们对能源的需求逐渐增大。 这也导致自然界中化石能源的逐渐衰减。人们已开始意识到节约能源对人类发展的重要性。对于居民的负荷用电占比也逐渐增大，因此居民节能用电对缓解能源消耗也发挥着重要的作用［1］。20 世纪80 年代由美国学者Hart 提出一种基于非侵入式的负荷监测技术（non-intrusive load monitoring，NILM）的用电负荷识别技术［2］。 该技术为居民实时提供了家用负荷用电信息。

随着智能电网和大数据的不断发展，国内外机构的研究学者逐渐投入到NILM 的研究当中。 文献［3］针对家用负荷识别特征量难以优化，以及识别算法收敛性较差的问题，于是提出用暂态特征作为特征量，然后运用DTW 算法计算测试模板与参考模板之间的相似度，从而达到有效的识别，但是对于功率相同的负荷会出现混淆的情况，因而识别率不高。 文献［4］采用家电的稳态基波电流和谐波作负荷特征的参数，用改进的鸡群算法作为负荷识别算法，可以准确地识别在各种复杂情况下的多种电器，但是当负荷特征出现重叠时，其识别准确率却较低。文献［5］针对在低频采样中负荷识别的研究，提出了基于多特征序列融合的非侵入式负荷辨识方法，此方法具有较高的辨识度和准确率，但对于家电负荷的功率相近的可以进一步进行优化。 文献［6］选取了采用低频采样得到的家用电器的稳态电流作负荷特征，将离散差分进化算法应用在居民侧负荷分解上，能够准确分解连续可变型、多工作模式型等复杂的家电负荷，但是可以发现当电流发生叠加时，对小电流的家电负荷识别精度下降。

上述研究都是在已知负荷类型的基础上，且大部分是采用的有功和无功功率作为负荷特征进行负荷识别，当有些负荷的功率相近时，会出现无法准确地识别电器类型。 针对以上研究问题的不足，于是在传统功率特征的基础上引入负荷的总谐波畸变率（THD）作为新的负荷特征。 其次，再分别使用粒子群算法优化支持向量机和使用蜉蝣算法优化支持向量机进行家用负荷的负荷识别。 最后，采用实测数据进行实验验证，可以得到采用蜉蝣算法优化支持向量机比起粒子群算法优化支持向量机将具有更加良好的准确性。

1 家用负荷特征分析

在非侵入式负荷识别过程中，常常选用传统有功P和无功Q作为负荷识别的特征。 研究时，可通过采集模块得到的电压和电流，计算得出有功P和无功Q的数据，具体计算公式如下所示：

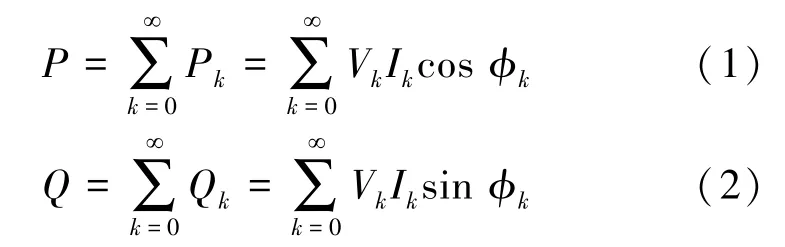
其中，P，Q，V，I分别表示有功功率、无功功率、电压以及电流；φ表示为电压和电流之间的相位差；k为谐波次数。 有功和无功负荷特征可以用来准确识别大功率电器种类，然而对于低功率的电器种类的识别不是很准确［7］。 由于不同负荷电流中所含谐波成分有所差别，故在采样电流数据的基础上，对各个负荷采用快速傅里叶变换得到其负荷电流的不同频率谐波。 在本文中除了选取传统有功P和无功Q作负荷特征外，还选用了不受谐波干扰的基波功率因数λ和负荷的总谐波畸变率（THD） 作为负荷特征以解决传统功率特征识别不足的问题。这里可给出研究分述如下。

（1）基波的功率因数。 此时需用到的数学公式为：

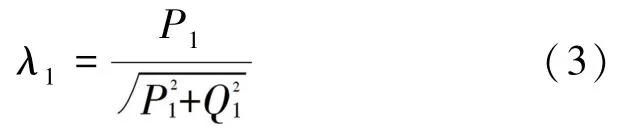
其中，P1表示基波的有功功率，Q1表示基波的无功功率。

（2）负荷的总谐波畸变率（THD）。THD指的是电流全部谐波含量均方根与基波均方根之比，其表达式为：

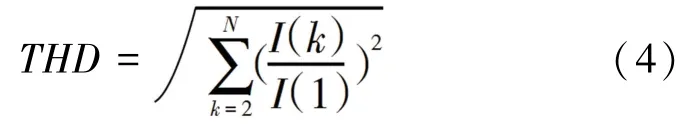
其中，I（k） 表示第k次电流谐波分量的均方根值；I（1） 表示电流的基波分量的均方根值。

2 基于MA-SVM 算法原理及实现

2.1 MA 算法介绍

蜉 蝣 算 法（ Mayfly Algorithm， MA） 是 由Zervoudakis 等人在2020 年研发提出、可用于解决FS 问题的一种新型智能优化算法［8］。 这是一种混合方法，结合了经典优化方法（例如PSO 、GA 和FA）的优点。 不仅寻优能力强，而且有着较大研究价值。 分析可知，蜉蝣属于星翅目（Ephemeroptera）昆虫，是古翅目昆虫的一部分。 由于这些昆虫主要在英国的5 月出现，因此得名Mayfly。 据估计，全世界有超过3 000 种蜉蝣。 从卵中孵化出来后，还需花费数年时间才能长成水生若虫，当其准备成年时才会浮出水面。 一只成年蜉蝣的寿命只有几天，直至完成繁殖目标。 为了吸引雌性蜉蝣，大多数雄性蜉蝣将成群结队与雌性蜉蝣进行婚庆舞蹈。 交配过程仅持续几秒钟，之后会将卵滴入水中，并且循环持续进行。 在Allan 等人［9］的著作中则详细提及了前述过程［10］。 MA 的组成部分可阐释为如下步骤［11］：

（1）雄性蜉蝣的运动。 由于雄性蜉蝣的运动方式总是成群结队，因此对于每一只雄性蜉蝣总是要根据自己和邻居的经验来调整位置。 雄性蜉蝣位置更新公式为：

其中，表示雄性蜉蝣在时间步长为t时在搜索空间中的当前位置，xi t+1是通过在当前位置上添加速度vit+1来改变的新位置。研究发现雄性蜉蝣需要行进至水面上几米处表演舞蹈来吸引雌性蜉蝣，此时假设其发展速度不是很快，且会不断地移动。 因此推得，雄性蜉蝣的计算公式为：

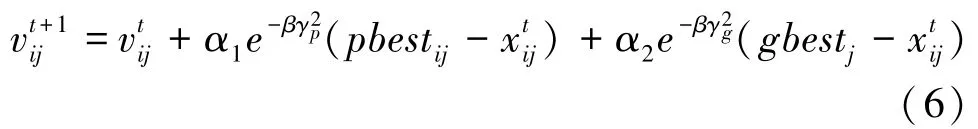
其中，是蜉蝣i在j维度t时刻的速度；代表t时刻的位置；α1和α2是社会作用的正吸引系数；pbest是代表蜉蝣访过的历史最佳位置；gbest代表最佳蜉蝣位置；β是蜉蝣的能见度系数，控制蜉蝣的能见范围；γp表示当前位置与pbest的距离；γg表示当前位置与gbest的距离。 对应的距离公式如下所示：

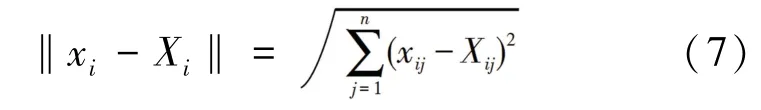
对于种群中最好的蜉蝣而言，表演其独有的上下舞蹈有着至关重要的意义。 故，这些最好的蜉蝣就必须不断地改变移动的速度，在这种情况下，计算公式可写为：

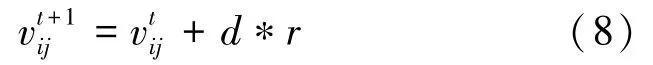
其中，d是舞蹈系数，r为［-1，1］之间的随机数。 这种上下移动在算法中引入了一个随机元素。

（2）雌性蜉蝣的运动。 与雄性蜉蝣不同的是，雌性蜉蝣不会成群结队，而只会飞向雄性蜉蝣去寻求繁殖。假设yi t为在时刻t时的蜉蝣i，对应的位置可通过增加速度来予以更新：

考虑到吸引过程是随机的，研究时可将其建模为一个确定性过程。 也就是说，雄性和雌性之间的吸引过程取决于当前解决方案的质量，即性能最佳的雌性被吸引到性能最佳的雄性处，接下来依此类推。 因此，考虑到极小化问题，速度的计算公式如下：

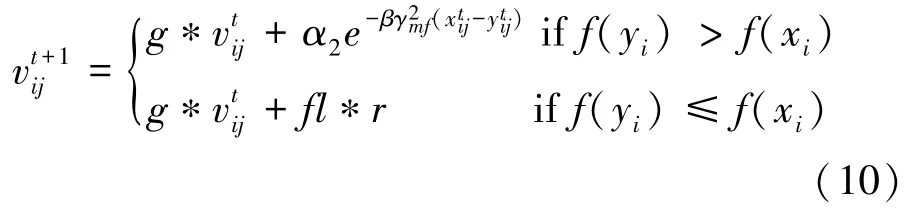
其中，表示第i只雌性蜉蝣在t时刻的速度的第j个分量速度；表示第i只雌性蜉蝣在时间t的维度j上的位置；α2和β分别表示前文定义的引力常数和可见系数；g表示重力系数；γmf表示雌性蜉蝣距离雄性蜉蝣的距离；fl表示在雌性未被雄性吸引的情况下的随机游动系数；r表示一个在范围［-1，1］的随机数。

（3）蜉蝣交配。 交叉算子表示2 个蜉蝣的交配过程：从雄性、雌性种群中分别各选择一个亲本。 选择父母的方式与雄性吸引雌性的方式相同。 需要指出的是，选择既可以是随机的，也可以基于设定的适应度函数。 对于后者而言，最好的雌性与最好的雄性繁殖，次好的雌性与次好的雄性繁殖。 交叉的结果是产生2 个后代，对应的数学公式定义如下：

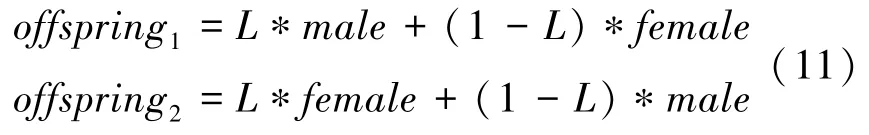
其中，male是父本；female是母本；L是一个特定范围的随机数。

（4）蜉蝣突变。 对新生成的后代进行突变以增强算法的探索能力。 将正态分布的随机数添加到后代变量中，如：

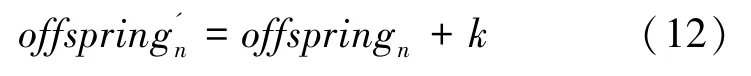
其中，k是正态分布的随机值。

2.2 支持向量机算法原理

支持向量机（SVM）是非参数、有监督的学习模型，其设计是立足于使分类器性能趋于更好的几何思想［12］。 SVM 的基本原理是在特征空间中找到一个使数据集中样本间距达到最大的分离超平面。 对于线性可分离数据集来说，支持向量机的算法目标是在N维空间（这里的N是特征的数量）中找到一个能清晰地分类数据点的最优超平面（或决策边界），而支持向量是最接近超平面的数据点［13］。 简言之，SVM 算法的目标是最大化分离超平面周围的边界，本质上就使其成为一个约束优化问题。

由文献［14］可知，求解多分类问题的实质就是将多分类问题的求解转换成二分类问题。 本文中针对一个M类分类问题，设给定的训练集为：

其中，xi∈Rn，yi∈Y ＝｛1，2，…，M｝，i ＝1，2，…，l。

由文献［15］研究可知，将寻求最优超平面的问题转换成二次规划问题，当引入适当的惩罚函数C和核函数后可得到问题的目标函数为：

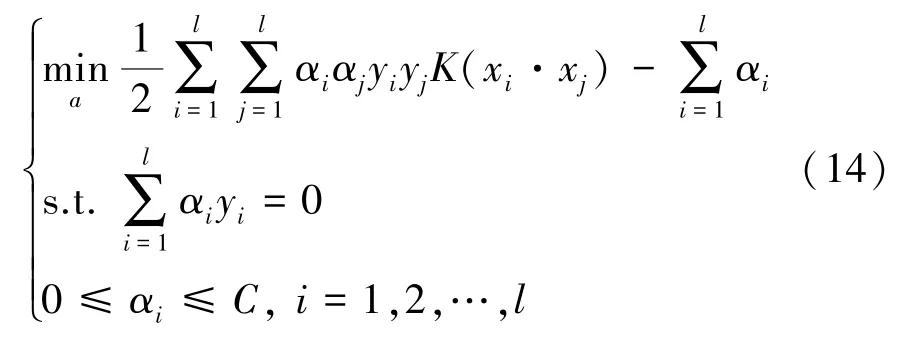
其中，K（xi·xj）＝（φ（xi）·φ（xj）） 为核函数。在本文中，研究选用的是Guass 径向基内核函数，即：

最终得到SVM 的最优决策函数为：

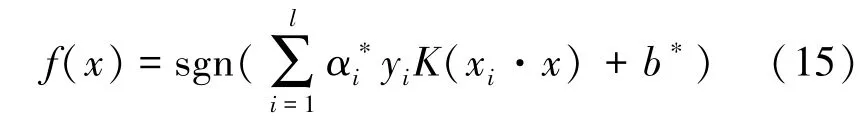
2.3 支持向量机的交叉验证

交叉验证（Cross Validation，CV）［16］是用来评判分类器性能好坏的一种统计分析方法，设计基本原理是将采集到的数据进行分组，将其中一部分作为训练集，将另一部分用作测试集，再利用训练集对分类器进行训练，用测试集来测试训练后得到的模型，从而得到分类器的性能评价指标。 在本文中，采用的是常见的交叉验证方法K 折交叉验证方法（ Kfold Cross Validation， K-CV）。

研究时，是将采集到的数据等分为K组，并对其中每个子数据集分别选作一次验证集，而其余的K -1 个子数据集作为训练集，按此方式将可得到K个模型，再用K个模型最终验证集的分类准确率的平均数来作为K-CV 分类器性能评价指标。 一般情况下，K大于等于2，在实际应用中多是从3 开始选取，尝试取2 时则是在采集的数据集数据量较小的情况。 K-CV 的优点是：可以有效防止出现过学习和欠学习状态的发生。

2.4 MA-SVM 算法在NILM 的实现

采用SVM 算法对负荷分类准确率较高，但是由于其对应的惩罚因子C和g参数具有不确定性。 故在支持向量机的惩罚因子基础上，可用MA 算法进行优化，如此一来就可对惩罚因子C和g进行寻优。这样做的好处就是克服了SVM 参数的不确定性，从而提高了家用负荷辨识的准确率。 MA-SVM 算法的步骤如图1 所示。

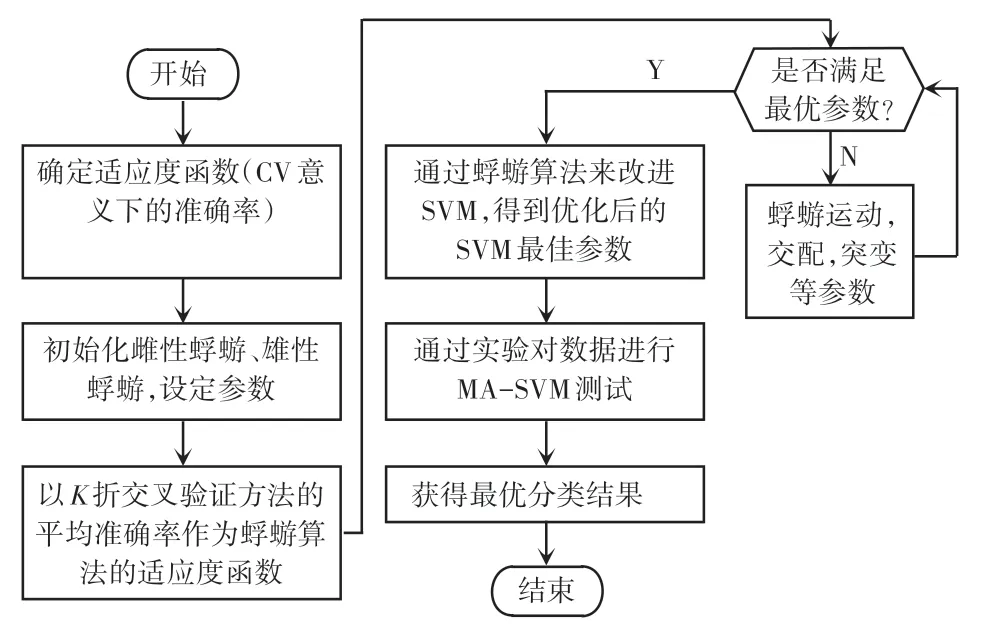
图1 MA-SVM 算法流程图Fig.1 MA-SVM algorithm flow chart

由图1 可以看出，先以K折交叉验证的平均准确率来作为蜉蝣算法的适应度函数，然后再初始化雄性蜉蝣、雌性蜉蝣来确定参数。 通过适应度函数值来判断SVM 算法中惩罚因子C和核函数g是否为最优。 若满足最优参数，就可得到蜉蝣算法优化后的最佳SVM 参数，最后通过实验采集的数据进行测试，得到最佳分类结果。 若不满足最佳参数，则蜉蝣还要历经运动、交配、突变等操作过程，直至获得最佳参数为止。

3 实验结果分析

为验证本文方法的运行效果，通过电能质量分析仪设备来采集家用电器数据，采集时间定为15 min，在此基础上再让家用负荷随机启停100 次，最后使用Powerlog 软件来分析采集数据，进行特征提取。 当得到用作测试样本和训练样本的数据集后，则分别采用MA-SVM 与PSO-SVM 算法进行辨识，其中，标签一为多用锅一（600 W）、标签二为多用锅二（450 W）、标签三为暖风机（500 W）、标签四为热吹风（1 200 W）、标签五为热水壶一（1 500 W）、标签六为热水壶二（1 500 W）。 MA-SVM 算法的训练集和测试集包含3 个负荷特征，分别为： 有功功率（P）、无功功率（Q） 及总负荷谐波畸变率（THD）。MA-SVM 算法参数：种群数量pop ＝100，雄性蜉蝣数量为50、雌性蜉蝣数量为50，最大迭代次数为200 次，远视系数为2，个体学习系数为1.0，群体学习系数为1.5。 变异率为0.01，参数a1＝1，a2＝1.5，a3＝1.5。 SVM 的核函数为RBF，其对应的平均适应度值和最优适应度值的变化范围如图2 所示。

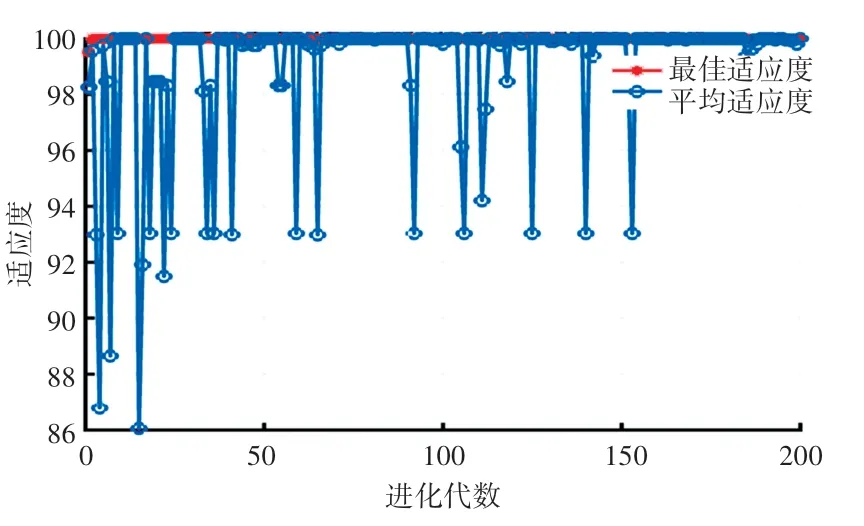
图2 MA-SVM 算法的最佳适应度和平均适应度的变化Fig.2 The change of optimal fitness and average fitness of MASVM algorithm

由图2 可以得到，当MA-SVM 模型取得最优参数时，SVM 中最佳参数c ＝62.311 4，g ＝2.490 2。取得最佳参数后，在测试集进行验证，运行结果如图3 所示。

图3 MA-SVM 算法的分类结果Fig.3 The classification results of MA-SVM algorithm

在相同数据集的基础上，PSO-SVM 算法参数：种群数量为pop ＝20，最大迭代数为200，局部搜索参数为1.5，全局搜索为1.7， 参数c1＝1.5，c2＝1.7。SVM 的核函数为RBF，其对应的平均适应度值和最优适应度值的变化范围如图4 所示。

由图4 可以得到，当PSO-SVM 模型取得最优参数时，SVM 中最佳参数c ＝12.073 5，g ＝2.679 4。取得最佳参数后，在测试集进行验证，运行结果如图5 所示。

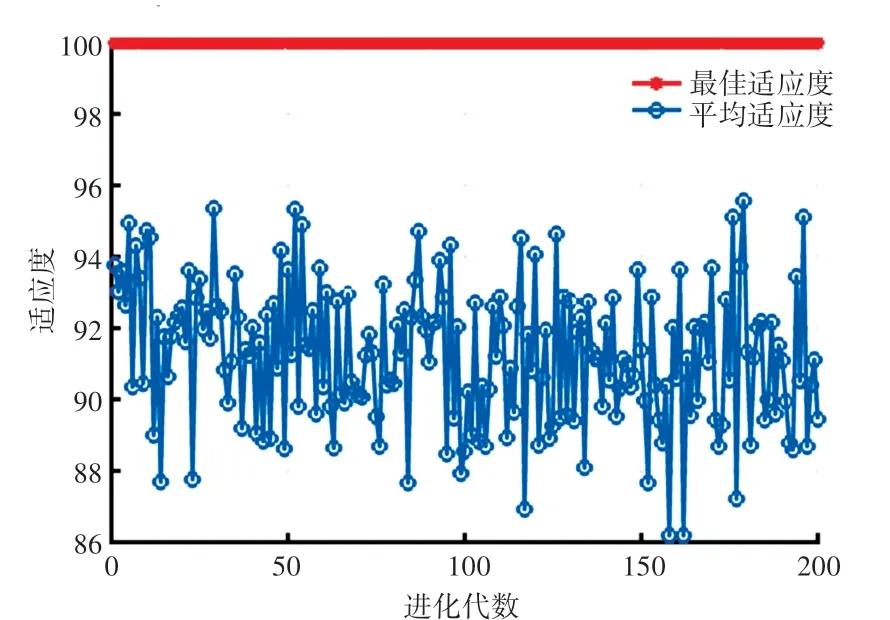
图4 PSO-SVM 算法的最佳适应度和平均适应度的变化Fig.4 The change of optimal fitness and average fitness of PSOSVM algorithm

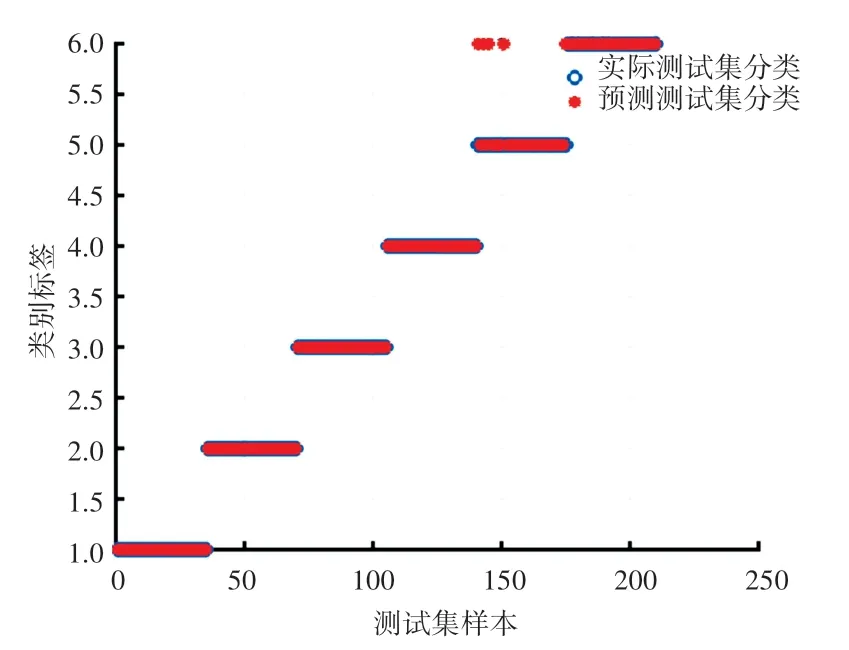
图5 PSO-SVM 算法的分类结果Fig.5 The classification results of PSO-SVM algorithm

在相同数据集基础上，由MA-SVM、PSO-SVM和SVM 进行分类后的6 种家用负荷识别准确率详见表1。

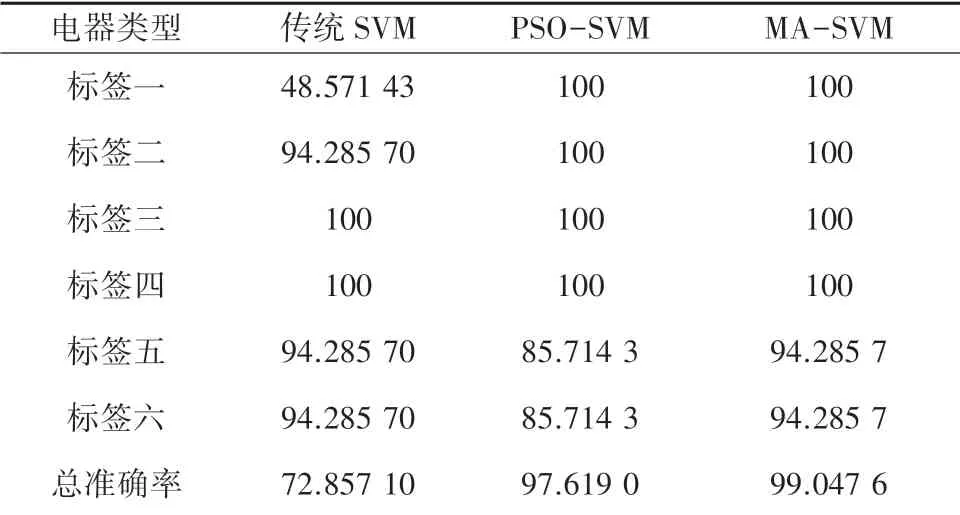
表1 6 种家用负荷识别准确率Tab.1 Identification accuracy of 6 kinds of household load %

由表1 可以看出，MA-SVM 算法比起传统SVM和PSO-SVM 算法具有较高的负荷准确率。 对多个低功率家用负荷具有良好的识别效果。

4 结束语

针对一些低功率家用负荷辨识效果较差的问题，本文采用有功P、无功Q及负荷的总谐波畸变率THD作为负荷特征，研发提出了蜉蝣算法来进行参数C和g的寻优，从而改进支持向量机的方法。 研究结果表明与PSO 算法优化效果相比，采用MASVM 对于低功率的负荷识别具有更好的准确性。