基于ARIMAX 的城市道路交通流短期预测模型

袁鹏程， 周天乐

（1 上海理工大学 管理学院， 上海 200093； 2 上海电科智能系统股份有限公司， 上海 200063）

0 引 言

随着交通拥堵和不确定性逐渐成为新常态，车联网、自动驾驶和大数据技术也得到了不断发展，交通流研究将会进入重要的变革期。 而交通流特性主要由交通流速度、密度和流量三个部分组成，其中交通流量尤为重要，并能直接反映交通运行状况。 精准短时交通流量预测就可以直观反映调查路段或地区的交通变化状况，为交通控制与管理提供可靠依据。 同时，也能为出行者提供准确地道路信息，避免不必要的拥堵。

目前，国内外对于交通流量预测已经做过很多研究［1］。 最常见的就是基于统计方法的模型和神经网络模型。 自上世纪七十年代末，ARIMA 模型［2］提出以来，即已广泛应用于各个领域［3］。 但由于ARIMA 模型的局限性等因素，往往会结合数据自身特点加以调整［4-5］。 例如，针对模型单一的问题，田瑞杰等人［6］提出一种时间序列与人工神经网络相结合的预测模型；基于时间序列分析方法，韩超等人［7］提出一种短时交通流实时自适应预测算法，减小遗忘因子进一步提高预测的性能；针对ARIMA 模型获取非线性特性的局限性，王晓全等人［8］加入广义自回归条件异方差—均值，相比于ARIMA-SVR模型和ARIMA-GARCH 模型得到了更好的预测精度；通过证实交通流量存在时序上的周期性，祁伟等人［9］引入季节性ARIMA 模型融合了邻近的交通流观察值和交通流数据的周期性。 此外，也有深度学习［10］、基于相空间重构理论的局部预测方法［11］等研究。 在上述交通流预测过程中仅仅利用了交通流量自身信息进行预测，并没有加入其他影响因素用于提高预测精度，丁永兵等人［12］通过结合路网结构，利用主成分回归建立上下游交通流回归模型，对模型残差进行ARIMA 建模，得到的ARIMAX 模型要优于ARIMA 模型。 但在交通领域并没有考虑将影响交通流量的因素（例如：道路占有率等）加入模型进行预测，而在其他的一些研究方向［13-14］就考虑将相关的参数加入模型进行预测，并取得了不错的效果。

构建传统时间序列模型的前提条件就是时间序列的平稳。 通常为了达到序列的平稳性会对原序列进行差分处理，但却会丢失了数据信息。 本文考虑引入道路占有率等因素来增加原始数据信息提高预测精度。 研究中，首先介绍了ARIMAX 模型的原理，接着对原始数据进行预处理，使其达到平稳的条件，然后通过利用Python 来搭建ARIMAX 模型拟合参数，继而对构建的模型加以验证，最后进行交通流预测。 通过分析最终评价指标结果可知，模型拟合效果较好，各种误差结果均偏小，达到了预期的效果。

1 模型理论

1.1 ARIMAX 模型

差分自回归移动平均模型（Autoregressive Integrated Moving Average Model，ARIMA 模型）是通过自回归移动平均模型（Auto Regression Moving Average Model，ARMA 模型）扩展而来的。 ARIMA模型中，先对时间序列进行差分使其达到平稳状态，再对差分后的时间序列建立ARMA 模型。 而ARMA 模型是将自回归模型（Auto Regression Model，AR 模型）和移动平均模型（Moving Average Model，MA 模型）有机组合而成的。 对此拟展开研究分述如下。

1.1.1 自回归模型AR

p阶自回归模型，记为AR（p），是一种处理时间序列的方法，用同一变数如x的之前各期，即xt至xt-p的值来预测xt的值，并假设各数值之间为线性关系。 公式如下：

其中，c为常数项；εt是均值为零，标准差为σ的随机误差项。

当引入延迟算子B，即Bn xt ＝xt-n，并将AR（p）模型中心化后，可简记为：

其中，Φ B( )＝1-φ1B -φ2B2-…-φp Bp，称为p阶自回归系数多项式。

1.1.2 移动平均模型MA

q阶移动平均模型，记为MA（q），是一种简单平滑预测模型，可根据时间序列xt至xt-p的平均值，以预测xt的值。 其公式如下：

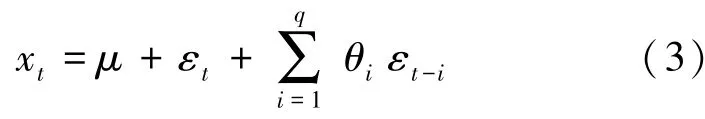
其中，μ是序列均值，θ1，…，θq是参数，εt，…，εt-q都是白噪声。

当引入延迟算子B，即可得到Bn xt ＝xt-n，并将MA（q） 模型中心化后，可简记为：

其中，Θ B( )＝1- θ1B - θ2B2-…- θq Bq，称为q阶移动平均系数多项式。

1.1.3 ARIMAX 模型

ARIMAX 模型就是带输入变量的ARIMA 模型，其构造思想是：假设响应序列yt{ } 和输入变量序列（即自变量序列）x1t{ }，x2t{ }，…，xkt{ } 均平稳，首先构建响应序列和输入变量序列的回归模型：

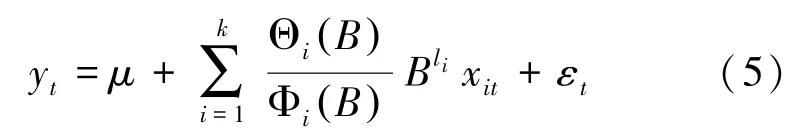
其中，B为延迟因子，即Bn xt ＝xt-n；Φi B( ) 为第i个输入变量的自回归系数多项式；Θi B( ) 为第i个输入变量的移动平均系数多项式；li为第i个输入变量的延迟阶数；εt{ } 为回归残差序列。

因为yt{ } 和x1t{ }，x2t{ }，…，xkt{ } 均平稳，而且平稳序列的线性组合仍然是平稳的，所以残差序列εt{ } 为平稳序列，即：

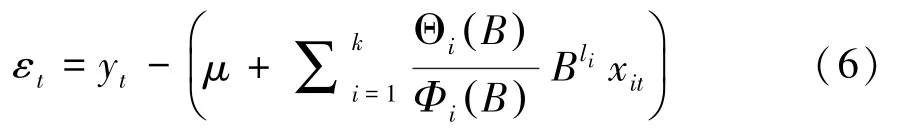
使用ARMA 模型继续提供残差序列εt{ } 中的相关信息，最终得到的模型为：

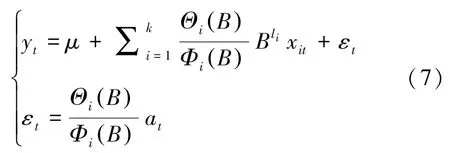
其中，Φ B( ) 为残差序列自回归系数多项式；Θ B( ) 为残差序列移动平均系数多项式；at为零均值白噪声序列。

2 参数估计

在选择了拟合模型后，就要利用时间序列的值确定模型的口径，即估计模型中未知参数的值［15］。ARIMAX 模型可以通过许多不同的方法来估计，包括将模型转换为非线性最小二乘法、GLS 或极大似然估计。 由于极大似然估计不需要从样本开始时丢弃观测值，或者需要从后期投射来创建观测值，因此比较适用于模型拟合。 未知参数的极大似然估计（Maximum Likelihood Estimation，MLE）就是使得似然函数、即联合密度函数达到最大的参数值［16］。 使用极大似然估计必须已知总体的分布函数，而在时间序列分析中，序列总体的分布通常是未知的［17-18］。 为了便于分析和计算，通常假设序列服从多元正态分布［19］。

设K维随机向量x ＝[x1，…，xk]-1的密度函数为：

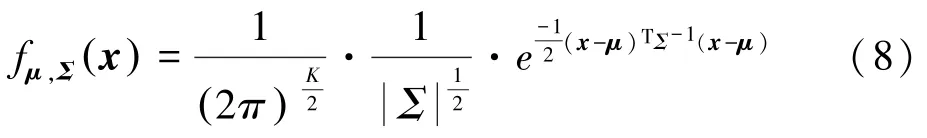
其中，K表示向量x的维度；均值向量μ是K维向量；协方差矩阵Σ是一个K ×K的对称正定阵，则称x服从K元正态分布，也称x为K维正态随机向量，简记为：x ～NK μ，Σ( ) 。 其似然函数为：

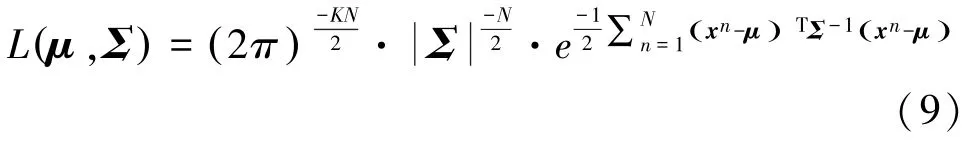
对数似然函数为：

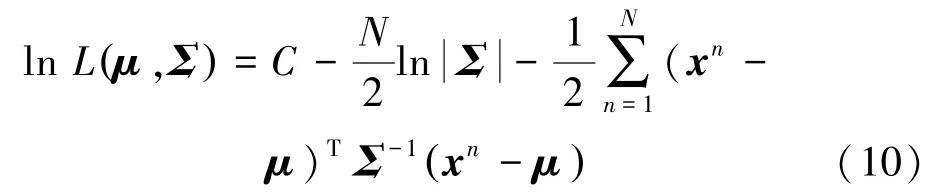
其中，为一个常数。 接着对μ，Σ求偏导、整理，最终得到极大似然估计为：

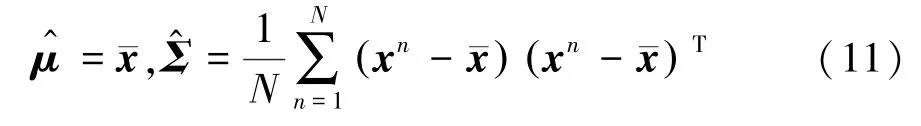
其中，N为样本个数。

3 评价指标

在前文基础上，还要对预测值的优劣进行评价，研究中用到的评价指标主要有：平均绝对百分误差、平均绝对误差、均方误差。 这里将给出分析表述如下。

（1）平均绝对百分误差（Mean Absolute Percent Error，MAPE），又叫平均绝对离差，是所有单个观测值与算术平均值的偏差的绝对值的平均。 平均绝对误差能够避免误差相互抵消的问题，因而可以准确反映实际预测误差的大小。 具体数学公式为：

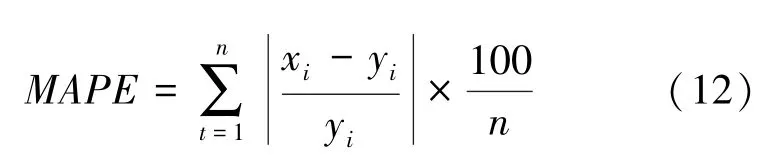
（2）平均绝对误差（Mean Absolute Error，MAE），又叫平均绝对离差，是所有单个观测值与算术平均值的偏差的绝对值的平均。 平均绝对误差能很好地反映预测值误差的实际情况。 具体数学公式为：

（3）均方误差（Mean-Square Error，MSE） 是参数估计值与参数真值之差平方的期望值。MSE可以评价数据的变化程度。MSE的值越小，预测模型描述实验数据则具有更好的精确度。 具体数学公式为：

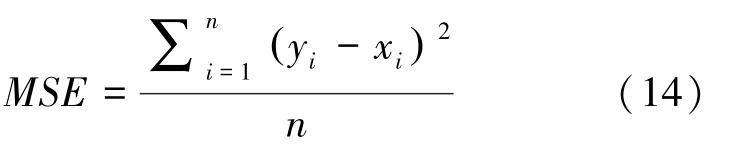
式（12）～（14）中，yi为预测值，xi为真实值。

（4）拟合优度。 是指模型的预测值对实际值的拟合程度。 度量拟合优度的统计量是可决系数（亦称确定系数）R2。R2最大值为1。R2的值越接近1，说明回归直线对观测值的拟合程度越好；反之，R2的值越小，说明回归直线对观测值的拟合程度越差。具体数学公式为：

其中，y为模型预测值；为流量观测值；¯为观测值的平均数。

4 模型构建

4.1 数据

本文采用的数据来自于美国加利福尼亚州交通局的公开数据集（Peformance Measurement System，PeMS），采用的是维克多维尔城市的某一条路从2018 年3 月5 日至4 月13 日工作日期间每5 min为间隔的交通流数据，共8 640 组数据，分析可得每天数据的基本统计特征见表1，截取前一周（即2018年3 月5 日至2018 年3 月9 日）的数据如图1 所示。

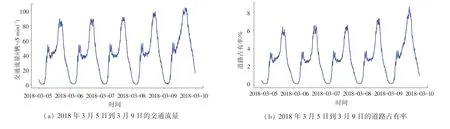
图1 一周的交通流量、占有率图Fig.1 Traffic flow and occupancy in a week

表1 交通流量、占有率数据的基本统计特征Tab.1 Statistical characteristics of traffic flow and occupancy

4.2 数据的平稳性检验

考虑到现存的虚假回归问题，在模型拟合前就要对各序列的平稳性进行检验。 只有当每个序列都平稳时，才能使用ARIMAX 模型拟合多元序列之间的动态回归关系。

观察图1 能发现交通流量与占有率的呈周期性变化，为了直观展示其规律，绘制交通流量和道路占有率的自相关图如图2 所示。 从2 个自相关图中，研究发现序列的自相关系数递减至零的速度相当缓慢，在很长的延迟时期里，自相关系数一直为正，而后又一直为负，显示出明显的三角对称性，这是一种具有单调趋势的非平稳序列。 为了将序列达到平稳状态，考虑采用简洁、有效的差分方法。 因此，研究中将原序列进行一阶差分，再对差分后的序列检验平稳性。 为了检验序列的平稳性，陆续提出了许多方法，其中应用最多的是单位根检验，而适用范围最广的则是ADF 检验，即增广DF 检验（Augmented Dickey-Fuller，ADF）检验。 检验时，原假设为序列非平稳，通过构造ADF 检验统计量：

图2 交通流量、道路占有率原始数据的自相关图Fig.2 Autocorrelation of original data of traffic flow and occupancy

其中，为参数ρ的样本标准差。

通过蒙特卡洛方法，可以得到τ检验统计量的临界值表。 当临界值小于0.05 时，拒绝原假设，认为序列平稳。 对一阶差分后的交通流量和道路占有率进行检验，检验结果参见表2。 观察ADF 检验结果显示，经过一阶差分后的交通流量｛∇yt｝、 占有率｛∇xt｝ 均达到平稳状态，因此可以用于构建ARIMAX 模型。

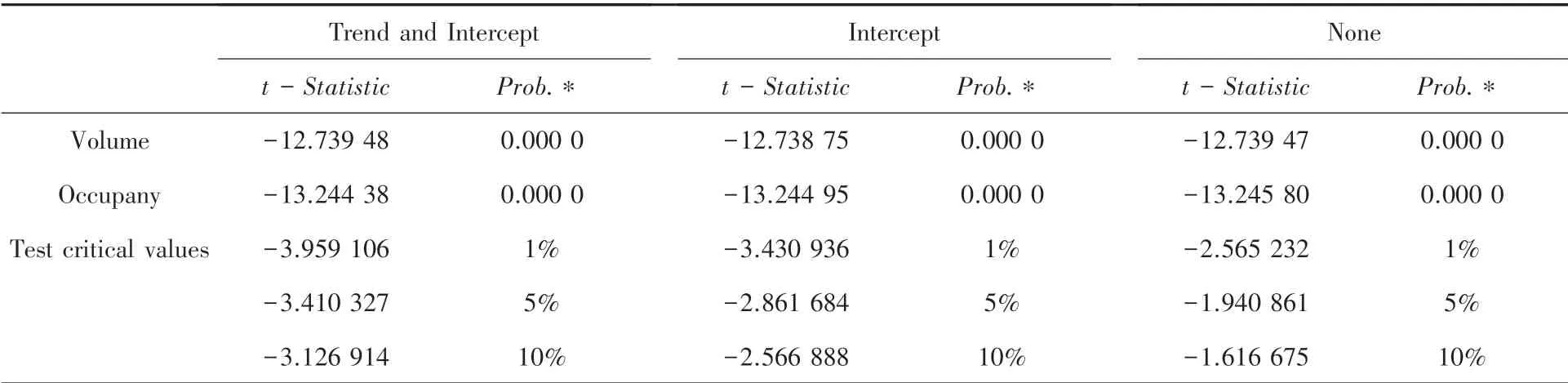
表2 交通流量、道路占有率一阶差分后的单位根检验Tab.2 ADF test after first-order difference of traffic flow and occupancy

4.3 模型的建立

经过平稳性检验，一阶差分后的交通流量和车道占有率平稳，可以建立动态回归模型。 首先，构建车辆流量 { ∇yt} 与占有率 { ∇xt} 的回归模型，由此推得数学公式为：

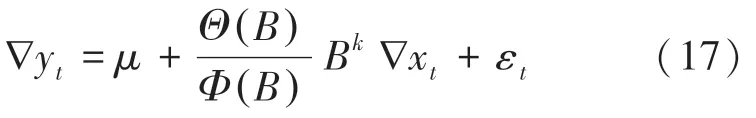
接下来，要确定自回归系数p与移动平均阶数q的值。 通过计算使模型的赤池信息准则（Akaike Information Criterion，AIC） 和 贝 叶 斯 信 息 准 则（Bayesian Information Criterion，BIC） 达到最小值的p、q值。 为此，分别计算各种p，q组合的AIC和BIC值，并绘制AIC、BIC的热力图，如图3 所示。 通过图3 来寻找AIC、BIC值最小的p与q的组合为（6，5）。再将差分后的序列带入模型，用极大似然估计进行拟合得到参数值，详见表3。 至此，最终模型可写为如下形式：

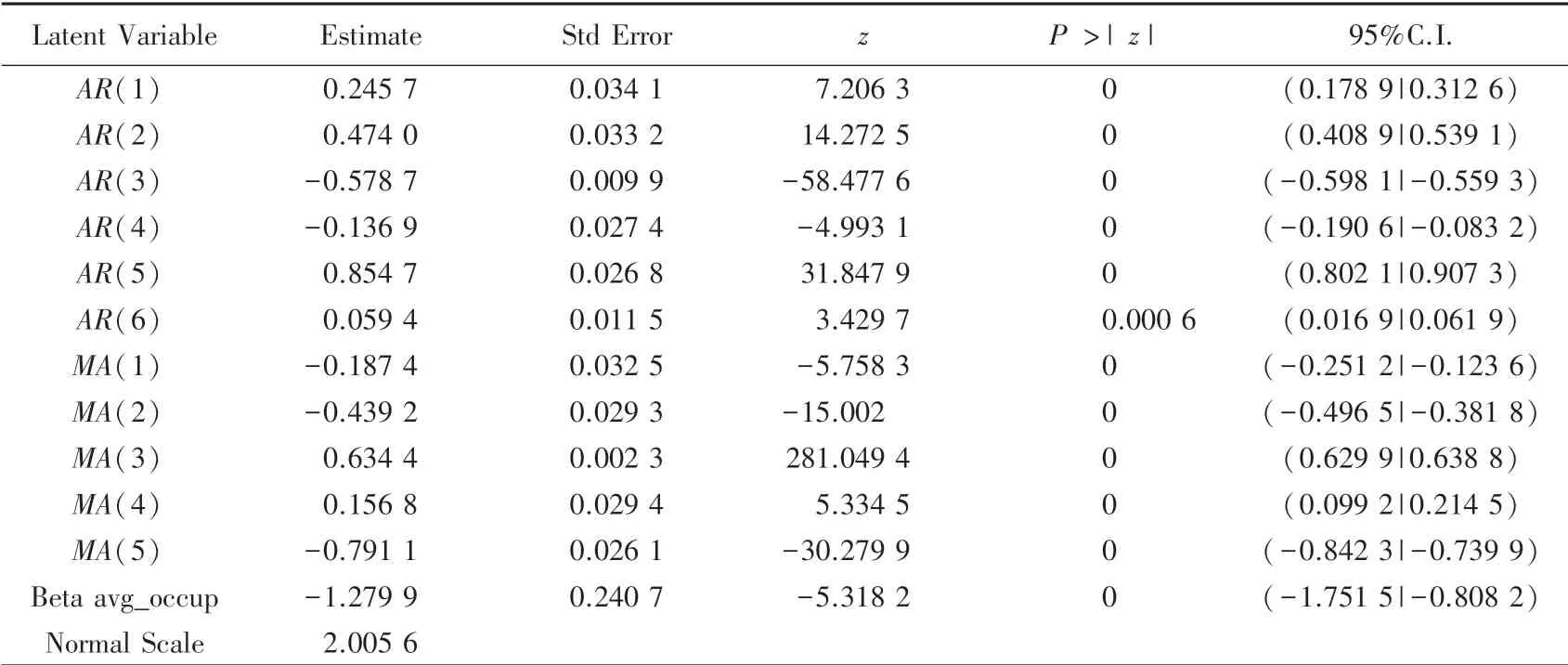
表3 ARIMAX（6，1，5）模型参数拟合Tab.3 Parameter fitting of ARIMAX （6，1，5）

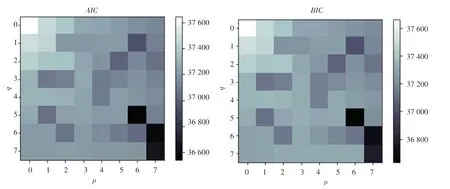
图3 p、q 各种组合的AIC、BIC 热力图Fig.3 AIC and BIC thermodynamic diagram of various combinations of p and q

考虑到差分的方法对确定性信息的提取可能不充分，因此还要进一步地对残差序列进行检验。 如果检验结果显示为残差序列的自相关性不显著，就说明ARIMAX 模型对信息的提取比较充分。 在此基础上，就是对模型的残差序列进行检验，判断是否存在残存有效信息。 为此，对其进行ADF 单位根检验和Durbin-Watson 检验（D-W 检验），结果见表4以及绘制残差的Q-Q 图，见图4。

表4 ARIMAX 模型残差检验Tab.4 Residual test of ARIMAX

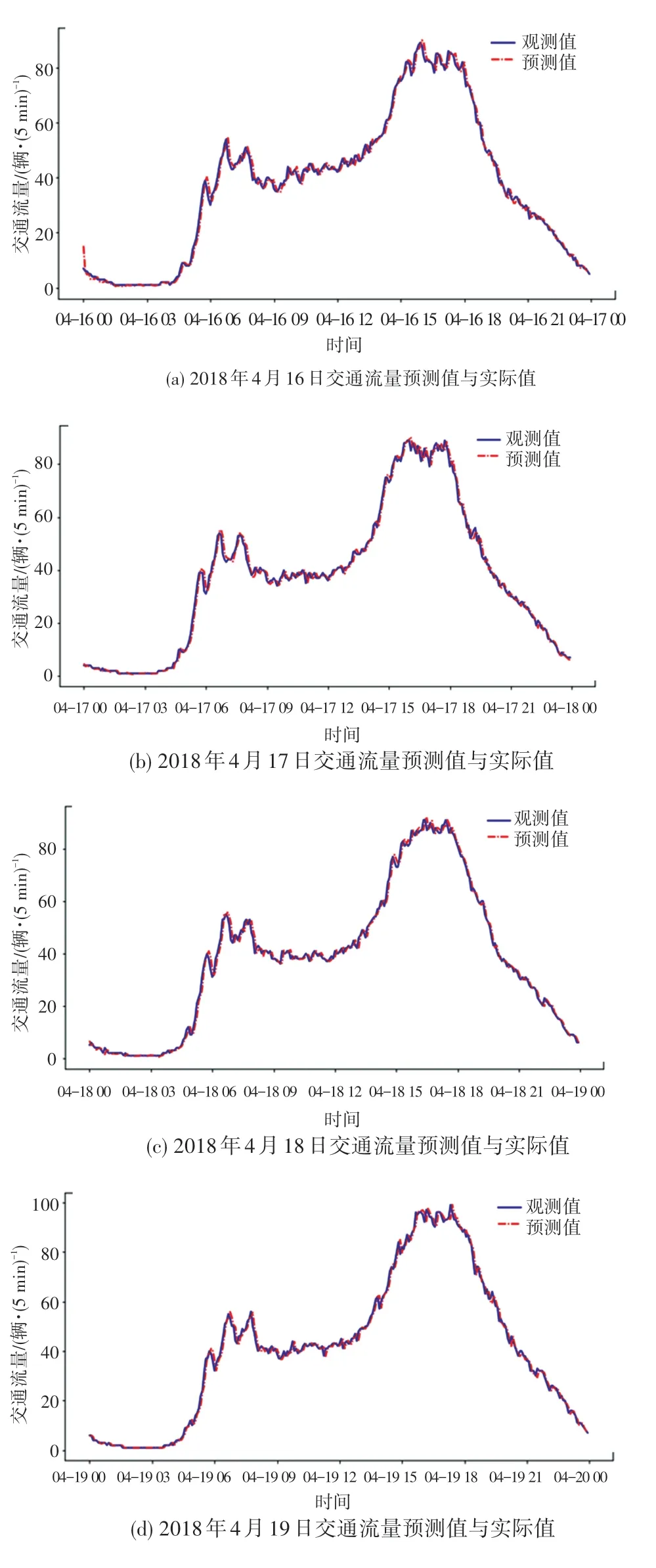
从表4 中可以发现D-W 值趋近于2，即接受原假设：残差序列不存在1 阶自相关性；单位根检验结果P值远小于0.05 说明残差显著平稳。 从图4 可以看出，散点基本落在直线两端，故残差满足均值为0 的正态分布。 满足以上条件后，就可用ARIMAX模型对此后一周的交通流进行拟合预测。 其中，这一周的预测流量与真实流量如图5 所示。

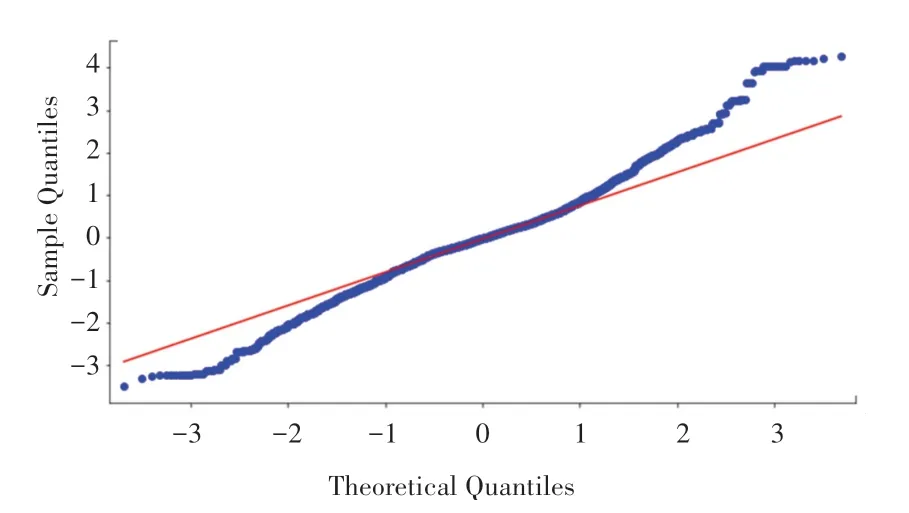
图4 ARIMAX 模型的残差Q-Q 图Fig.4 Residual Q-Q diagram of ARIMAX model

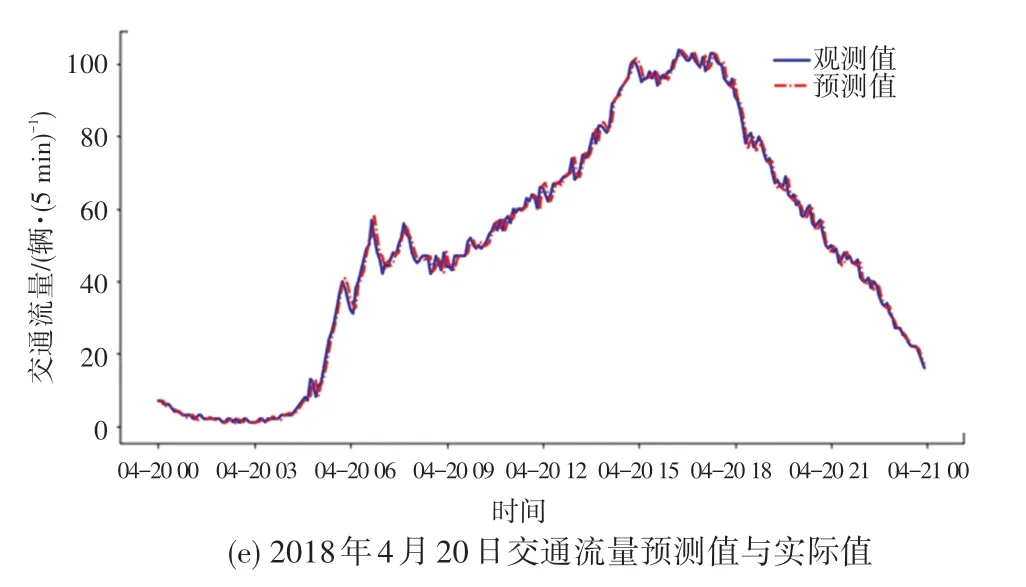
图5 预测流量与真实流量值Fig.5 Comparison between predicted and actual data

然后用平均绝对误差、均方误差、平均绝对百分比误差来衡量交通流量实际值与ARIMAX 模型的预测值（见表5），并计算模型的拟合优度为0.876 95。

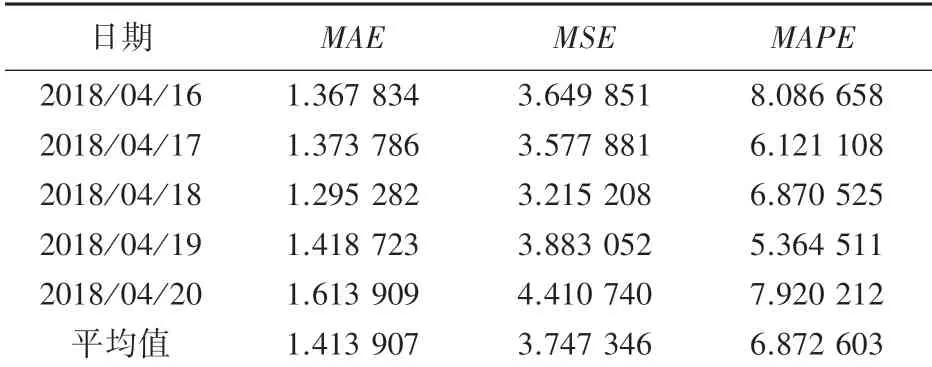
表5 预测与实际值的MAE，MSE，MAPETab.5 MAE，MSE and MAPE of predicted and actual data

通过模型可以发现，平均绝对误差、均方误差分别为1.47 和3.74，效果较好， 并且一般认为MAPE的值低于10%时预测精度较高，本文中MAPE仅为6.87，说明ARIMAX 模型预测效果较好。

5 结束语

构建ARIMAX 模型的过程与传统的ARIMA 模型类似，但与ARIMA 模型相比，丰富了数据信息，从而提高了预测的精度。 将交通流量、道路占有率作为输入序列，先要确保其序列的稳定性，为此采用差分来提取确定性信息。 经过一阶差分后，通过单位根检验，序列达到了平稳形态。 接下来，就是构建ARIMAX 模型，以及确定ARIMAX 模型的阶数。 在模型定阶过程中，相比于直接观察绘制的自相关、偏自相关图确定p、q值的办法，本文通过计算所有p与q组合的AIC和BIC，寻找使得AIC和BIC最小的那一组数值。 如此一来，既提高了精确度，又节省了调参的时间，预测效率明显提高。 在模型阶数确定后，利用极大似然估计的方法来拟合参数，得到了一个ARIMAX 模型。 虽然拟合求出了参数模型，但是并不能保证差分的方法能够充分提取确定性信息，因此还要进一步来检验残差。 经过D-W 等方式检验、并发现残差不存在自相关性后，就可以用得到的ARIMAX 模型进行交通流量预测。 为了防止偶然事件的产生，研究中预测了接下来一周的交通流量，并运用多种评价指标进行验算。 最终结果显示，采用道路占有率作为外生变量的交通流量ARIMAX 模型能够很好地拟合流量序列的变化规律，也有着良好的预测精度。 而且作为统计类的模型其未知参数对比于神经网络要少得多，具有更快的预测速度，既满足了交通流预测的实效性，也得到了很高的预测精度。

本次研究中，虽然利用道路占有率作为外生变量加入到了交通流量的预测中来减少序列预处理时差分所减少的有效信息量，但是并没有研究道路占有率的加入对预测精度具体提高了多少的百分比，以及道路占有率的加入能否弥补因差分所带来的有限信息量的丢失，这些都是未来课题的有效考察重点。 而且作为交通流参数，还有如速度、车头时距等，若将其也加入交通流量的预测模型中，能否提高预测的精度以及弥补因差分丢失的信息内容，也是下一步需要深入探讨的研究方向。