兼容bfloat16 的高速浮点加法器设计

胥 涛， 秦水介， 邓 全

（1 贵州大学 贵州省光电子技术及应用重点实验室， 贵阳 550025； 2 国防科技大学 计算机学院， 长沙 410073；3 贵州大学 大数据与信息工程学院， 贵阳 550025）

0 引 言

随着信息时代的到来，图像识别、深度学习、数字信号处理和人工智能等应用技术在不断地发展，需要处理的数据量正与日俱增，对于计算能力的要求也越来越高。 由于浮点数科学计数的方式，在图像识别、机器学习等领域得到了越来越广泛的使用，对于数据计算速率的提升有很大的作用。 由于浮点的加法、减法、转换、比较都可以转换为加法或者复用加法的部分计算来实现，使得浮点加法在运算中使用频率占50%以上［1］，所以浮点加法的性能提升对于浮点计算能力的提高有着非常重要的意义。

在机器学习等领域发展过程中发现，一般情况下不需要用到32 位和64 位的高精度数据，而bfloat16 的数据格式比IEEE 754-2008 定义的16 位数据表示范围更大，对比32 位和64 位数据而言，尾数较小、精度较低在计算时容易在舍入上出现错误；而精度低也表示在相同内存下，bfloat 格式可以存放更多数据，数据的存取移动速度更快，同时在计算部件的实现上也会更加简单。

bfloat16 格式是指1 位符号位、8 位阶码、7 位尾数组成的浮点数，形式上相当于单精度浮点数的高16 位；同时相比IEEE 半精度浮点阶码更大，尾数更小，可以发现就能在降低精度的情况下表示更大范围的数据。 由此有一些处理器已经将bfloat16 数据的计算加入设计规划，比如ARM 宣布将bfloat16 数据格式加入下一版本的Armv8-A 架构［2］。

现在主流的浮点计算还没有实现兼容bfloat16数据的相关计算，为了满足对浮点计算速率更高的要求，本文提出一种支持bfloat16 的高性能浮点加法器设计，包含设计要点，性能报告等。 本文工作包括算法修改、缩拍设计、bfloat16 计算兼容。 其中，算法修改是为了更好地实现缩拍设计，在原来的3 拍流水线设计上，各拍计算功能分配合理，频率相对较高，但绝对延时为3 拍。 为了满足2 拍流水线的设计，优化后的算法将前导零预测和尾数计算改为并行计算，减少了整体的计算时间，将绝对延时减为2拍，但是每拍的计算操作更多，功率更高。 算法修改后将流水线缩减为2 拍可以尽可能避免频率减小。

实验数据表明，最终设计相比原始设计频率下降1.36%，达到2.16 GHz，面积增加14.01%，功率增加53.31%，为2.181 1 mw。

1 高性能浮点加法器设计

浮点加法算法主要可以分为单通道计算算法、双通道计算算法、三通道计算算法等，主流为双通道算法（Two-Path）和三通道算法（Triple-data-path）。

浮点加法计算过程简单，分为阶码相减、对阶操作、前导零预测、尾数相加、规格化舍入等运算步骤，如图1 所示。

图1 浮点加法流程Fig.1 Floating-point addition flow chart

1.1 3 拍流水线加法器设计结构

本设计是基于主流的TWO-PATH 算法上做出的改进，原始的加法器算法设计的是一个3 级流水线的加法器部件，简单的算法流程图如图2 所示。 原始算法按TWO-PATH 结构设计，第一步是数据的预取：首先按照输入信号的变化分辨操作数的精度，依据不同的浮点精度选取不同长度的阶码、尾数部分，对2 个操作数进行阶码相减分辨操作数的计算符合near 和far中哪一条路径。 对于TWO-PATH 算法依据浮点加法的计算方式将加法分为near path 和far path 两条路径，两者以阶码的差值相区别，当阶码的差值小于等于1时，加法对应near path 部分结果，当阶码差值大于1时，加法结果为far path 路径结果。

图2 浮点加法3 级流水线示意图Fig.2 Schematic diagram of the three-stage pipeline for floatingpoint addition

第二拍的操作是将near path 路径数据的尾数部分进行前导零预测计算，计算前需将数据右移一位的同时在最高位补1，这是由于规格化浮点数的尾数部分总是默认舍弃最高位1，在计算过程中还要回复原始数据计算。 根据操作数阶码的差值和尾数的大小比较确定右移的位数，判断操作数的大小。根据小数靠大数的原则右移尾数部分，然后根据前导零预测的数据左移操作数尾数部分，最后进行尾数的加法操作。

第三拍的计算操作是舍入和数据选择，根据计算指令规定的舍入模式对加法的结果进行数据舍入，同时根据浮点计算的规则和操作数的情况，分辨结果是near path 路径结果、还是far path 路径结果、或者是特殊值。

1.2 优化的浮点加法器设计结构

优化算法的结构也是基于TWO-PATH 的算法，其中对于关键路径的时序进行了优化，将计算过程的绝对延迟缩减到2 拍，且支持流水线操作。

浮点加法3 级流水线的设计见图2，本文提出加法计算结构将计算的步骤缩减到2 拍，即：E1 和E2。 在初始算法设计3 拍流水线的基础上，为了提高计算速度，降低流水线拍数，在第一拍完成数据分解和计算阶码差值后，将较小操作数尾数部分对阶的右移操作也放到第一拍，加快near path 路径计算；在第二拍完成尾数部分的补码加法，计算尾数部分的前导零预测的结果，取消对操作数规格化的操作，改为对结果进行规格化，然后对结果进行舍入计算，减少了near path 的计算时间。

原始算法的加法设计在划分流水线时，将数据的右移对阶部分、前导零预测部分、左移规格化部分都设定在同一拍的流水上，由于前导零预测的复杂性，大大占用了节拍时间。 为此在新设计中，为了在缩拍后避免时序的冲突，将阶码对阶定制在第一拍的计算中，将前导零预测和计算排定在第二拍中，看起来似乎加大了第二拍的运算时间，然而对于整体计算过程而言，原设计在尾数相加之前的对阶操作、前导零预测和规格化左移是一个连贯有序的过程，后续的规格化左移只能等待前两者完成后才能启动；而对于新设计而言，在上一拍已经进行了对阶右移操作，而规格化左移的计算是针对结果去做的，这并不会影响正常的尾数加法，所以前导零预测和尾数的相加并行进行，如此则缩短了整体的计算时间。 综上缩拍的结果符合设计的要求，在保证频率的情况下减小整个加法的计算时间，完成了流水线缩拍设计。

在此基础上，根据TWO-PATH 算法的规则，分别选取符合far path 和near path 的数据建立测试功能点，对于特殊数如：无穷大（inf）、NaN（not a number）等也考虑在内，接下来基于这些功能点编写定向测试激励测试功能完整性。

在做缩拍设计时，会遇到的较为典型的信号传导和时序匹配问题，比如功能验证时发现阶码计算出错的问题，排查发现是阶码信号传递的判定信号和前导零预测结果的传递判断信号相同，但是两者在计算时是一个串行的关系，所以出现计算错误。这是在节拍控制上对于相关问题考虑上发生的疏漏所致。 所以需要考虑到数据传递和计算在时序分配上的关系，从而避免设计冲突。

1.3 兼容bfloat16 的设计

1.3.1 设计结构

本设计将bfloat16 格式的计算放在16 位浮点加法模块中，如果将bfloat16 浮点数看做32 位IEEE标准数据的前半部分计算，将其和32 位单精度加法结合，那么实现起来会很简单，对于设计的改变较小；但是这样设计考虑到精度混合计算时，在一个64 位双精度计算部件中只能兼容2 个32 位单精度计算、或2 个bfloat16 计算、或4 个半精度计算；所以研究中将其与IEEE 格式的16 位半精度加法计算结合在一块，这样一来64 位双精度计算部件可以兼容2 个32 位计算、或4 个bfloat16 计算、或4 个半精度计算，利用计算部件的复用实现兼容bfloat16 格式，减小资源的消耗，兼容bfloat16 的半精度加法的设计如图3 所示。

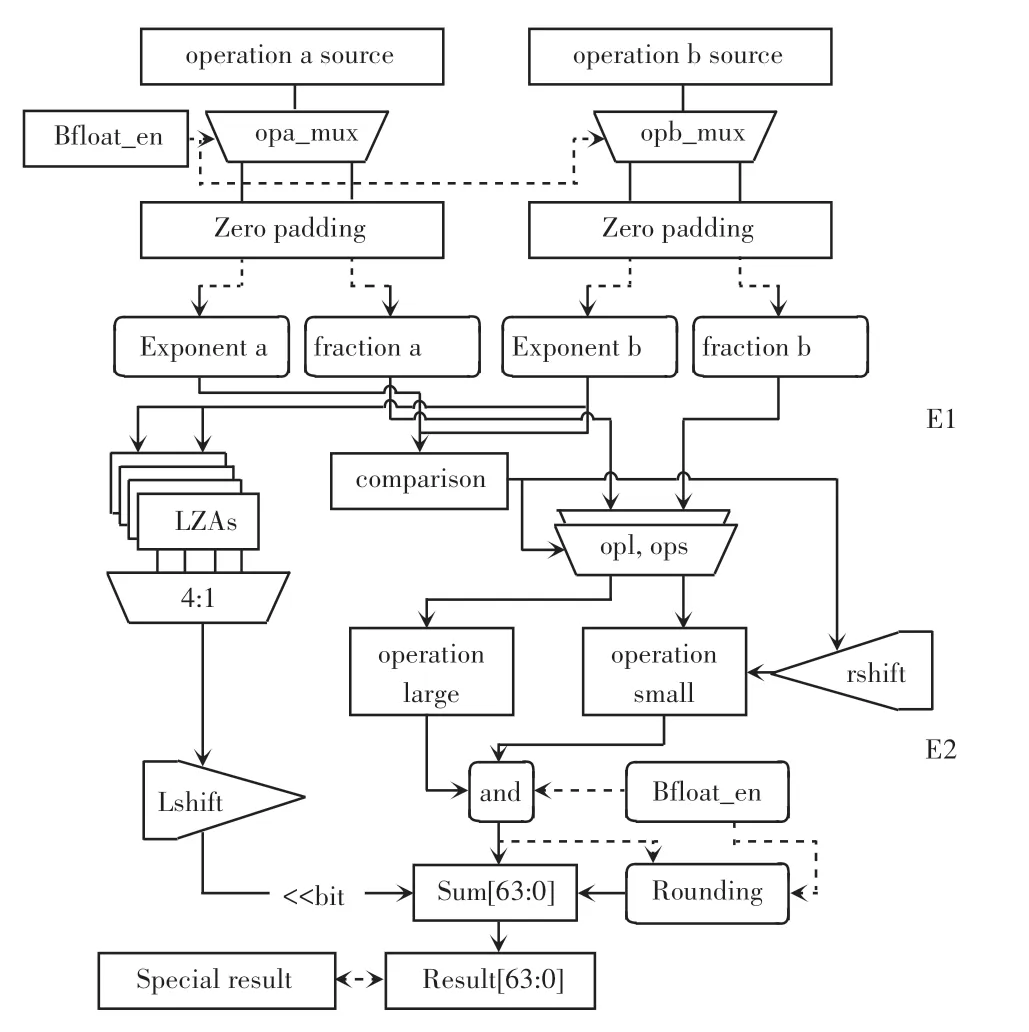
图3 兼容bfloat16 的半精度加法Fig.3 Half-precision addition compatible with bfloat16

对于半精度的数据而言只有5 位的阶码长度，所以要达到兼容bfloat16 的情况要扩展高位，为了不影响正常的半精度阶码计算需要在高位补0，而尾数的计算，为了保证bfloat16 数据计算的正确性，需要在数据分解时，将尾数部分放在高位，在低位补0。 为了区分计算需要添加bfloat 使能信号，在前导零预测中bfloat16 最多可移动位数是7，小于半精度的10 位，所以前导零预测的部件复用对于结果不会产生影响。 在舍入计算中同样需要区分两者的不同有效部分，由于舍入的判定都是由有效位后的数据和舍入模式决定的，计算结果选取也要选择相应的有效位数，这些都需要考虑bfloat16 和半精度浮点的区别。

设计工作要考虑bfloat16 数据和正常浮点数的计算差别，包括数据格式、特殊数选取、舍入模式等方面。 基于浮点计算的共通之处则要尽可能复用正常浮点的计算通路减小功耗。

在进行了兼容bfloat16 计算的设计后，先利用写好的定向测试激励验证正常浮点数计算功能是否破坏，再根据TWO-PATH 算法和bfloat16 的数据格式建立功能点，重新编写定向激励测试设计的功能是否成功。

1.3.2 bfloat16 对于特殊数的处理

对于无穷大、NaN 数、subnormal 数的格式和IEEE 标准类似，只是数据的位数不一致。 其中，无穷大数和NaN 数都是阶码为全1，尾数为全0 和不为全0 的数；subnormal 数是阶码为0，尾数不为全0的数；subnormal 数阶码为0，但表示的数据阶码在计算时等同于1。

对于这些特殊数据在计算时的处理使用的RISC-V 的处理情况，正负零相加减，结果为正零；若符号位相同，则符号位取任意操作数符号位。NaN 数与任意数据相加减结果为canonical-NaN，两NaN 数相加减结果也为canonical-NaN；正无穷大加减数据结果为正无穷大，负无穷加减结果为负无穷，正负无穷相加减结果为canonical-NaN。

对于这些特殊数据的计算，为了实现特殊结果的输出，在数据输入后就会进行特殊数的判断，比较阶码和尾数部分是否全为1、或全为0，从而判断是哪一种特殊情况，根据设计规则输出标准结果。

2 实验

2.1 实验环境

利用核级环境调用加减法指令测试实验功能准确性，利用DC 综合工具进行综合仿真。 实验分为设计修改、定向测试激励验证、EDA 软件综合PPA对比。

分析可知，验证即是芯片设计过程中值得关注的重要问题，随着芯片功能的不断强大，验证环境涉及的各类情况越发复杂，需要占据设计环节越来越多的时间和工作。 本设计只需要验证BF 浮点16位加法功能的正确性，只使用定向测试激励验证设计功能。 简单来说，设计对应的bfloat16 的计算数据，准备正确结果作为比对值，在计算结束后将计算结果与预设值比较，这些过程都由汇编指令完成。

对于本设计的验证，选择了利用浮点指令的定向激励做测试，定向测试激励都利用risc-v 支持的汇编指令编写，整个过程具体分为：调用访存指令读取数据、利用浮点搬运指令放入浮点寄存器、调用浮点加减指令、计算结果写回寄存器、写入正确结果对比值、调用比较指令、输出比较结果。 数据选取考虑到了正常的数据计算（包括near path 和far path 的各样需要移位的情形）、非特殊数的临界数据计算、无穷大和NaN 数等特殊数的计算情形。

本设计使用的EDA 软件综合工具来对设计进行综合验证，使用软件综合的结果可得到较为优化的时序效果，会自动对设计中部分参数进行优化，比如设计尺寸、电路拓扑结果、时序约束等，所以EDA的软件综合结果比其他工具在面积、速度上更加精简。 实验比较了原始算法、缩拍新算法设计、兼容bfloat16 算法三种设计。

2.2 实验结果

EDA 综合数据符合预期。 原始算法、改进算法和兼容bfloat16 格式的EDA 综合数据见表1。

表1 EDA 综合结果Tab.1 Comprehensive results of EDA

表1 中，数据前四列为EDA 工具综合出的4 个路径组，对应的数据为该路径的slack 值；后三列为设计占用的硬件资源。 slack 值代表的数据为设计要求时间和dc 工具模拟出的时间的差值：当slack为正数，表示在要求时间内可以完成该路径计算；为负值，表示计算时间超过约束值。 本设计中使用的约束时间为0.455 ns，原始算法恰好满足结果，其频率达到2.2 GHz；对于改进算法，由于进行了拍数缩减，使得在尽量保持频率的情况下减少了硬件计算资源，其频率达到2.16 GHz；兼容bfloat16 计算的算法，在设计实现下其频率为2.17 GHz，与原算法相比在缩减流水线兼容bfloat16 计算的情况下其频率下降1.36%，面积增加14.01%，功率增加53.31%。

定向测试激励测试结果：bfloat16 浮点加法减法计算，特殊数计算结果均符合预期，正常IEEE 标准浮点计算结果正常。

3 结束语

本设计提出一种兼容bfloat16 格式的高速浮点加法设计，在保证正常的16、32、64 位浮点计算的同时将执行流水线缩减至2 拍，频率可达2.17 GHz，功耗为2.181 1 mw。本设计可以保证在深度学习、图像识别等领域进行计算时使用bfloat 格式浮点数计算，提高计算速度；但由于是在原浮点加法部件上进行的兼容设计，整个计算的功能变得庞大，虽然做了流水线缩拍设计，但整个部件的频率还是有略微下降，并且功耗加大，所以还需进一步改善设计的功耗面积等相关方面。