基于SRAD-DWT 算法的显微图像降噪模型

熊海晨， 么 娆， 孙乐萌

（上海工程技术大学 航空运输学院， 上海 201620）

0 引 言

在工业生产过程中，由于工艺流程或不良环境对零部件造成损伤和腐蚀等情况的存在，就可能导致产品生产规格不合格，严重时还会造成生产线停产以及安全事故。 为此提供零件损失评估和修复依据，获得清晰的显微图像数据就显得格外重要，同时，也可为后续如图像拼接、损伤识别、工艺流程提供数据支持［1］。

在过去的几年中，许多算法已经被开发出来消除各类图像噪声。 本文提及6 种降低显微图像噪声的方法： 数学形态学（MM）、中值滤波（MF）、离散余弦变换（DCT）、离散小波变换（DWT）、非局部均值（NLM）、三维块匹配（BM3D）。 班晓娟等人［2］利用噪声信号的特点，结合多种单一结构元素提出一种多尺度形态学降噪滤波方法，该方法虽然在图像高频区域信号处理方面有不俗的表现，但是对于图像的平滑区域散斑噪声抑制能力非常有限。 王建新等人［3］基于中值滤波的不足，提出一种应用于海面光学图像均值滤波算法。 该算法抛弃了灰度值2 个极端的像素点，可以有效地减少椒盐噪声，但是在边缘细节的保留能力上还有所欠缺，当图像细节信息较多时，依旧会出现边缘模糊等情况。 鲍炜［4］利用coif-5 小波做5 层小波分解并引入相关统计参量进行估计提出一种自适应阈值的离散小波降噪算法，实验表明该算法优于硬阈值和线性阈值的降噪方法，可以获得更高的信噪比和更小的均方根误差，但是噪声较多在图像的边缘细节保留能力上略显不足。 Tounsi 等人［5］提出了一种采用NLM 滤波器和基于自适应掩模滤波技术的降散斑噪声技术。 虽然这种算法保留了突出的特征信息，但在平坦区域表现出较低的散斑噪声抑制能力。 Santos 等人［6］提出了一种基于块匹配协同过滤和新型随机距离技术的降噪算法。 尽管该算法具有极好的特征信息保存能力，但斑点噪声仍然存在于图像的均匀区域中。

针对这些算法对于去除显微图像散斑和高斯的混合噪声时会存在丢失边缘信息、比如纹理模块和其他重要的细节，或者去斑点噪声不明显的问题，从而得不到研究想要的目标数据要求。 本文提出一种平滑区域与边缘区域分别处理的改进SRAD-DWT算法。 使得平滑和锐化这一组相对的处理方式同时作用于显微图像降噪过程中。

1 显微图像退化及噪声分析

在图像获取过程中造成图像退化的原因数不胜数，但最主要还是图像传输和保存过程中导致的，同时由于不同图像系统、拍摄对象和相机之间存在相对运动，乃至空气媒介都有可能使图像变得模糊不清、产生噪声、照片对比度降低等种种现象［7］。 当下，通常见到的退化图像一般是运动的模糊类型、高斯模糊类型和离焦的模糊类型，有时还有多种模糊混合在一块的情况。 图像不清晰时，有2 个因素会影响这一过程。 其一就是退化的模糊函数，也就是所说的点扩散函数；其二是噪声因素。 这里拟对此展开研究分述如下。

1.1 图像退化类型

点扩散函数会随着图像模糊种类的不同而变化，想要把模糊参数更精确地找出来，就要把不同的图像模糊类型进行分类处理［6］。 比如，如果将运动模糊类型和散焦模糊类型的图像分开来看的话，运动类图像找到相应的运动模糊方向和运动模糊长度就可以了。 具体来说，对于模糊类型的判别，傅里叶变换［8］是一个很重要的依据。

不同模糊类型图像的傅里叶变换频域图像如图1 所示。

图1 清晰及各类模糊图像频域图Fig.1 Clear and all kinds of fuzzy image frequency domain map

根据上述傅里叶变换频域图像的不同表现，将固定放大倍数（200 倍）拍摄的金属样件表面磨损图像也进行相应的数学变换得到对应频域图像，如图2 所示。

图2 显微图像及其对应频域图Fig.2 Microscopic image and its corresponding frequency domain map

根据各对应频域图像，分析后可以得出显微图像存在轻微的散焦模糊退化情况。 究其根源，导致此结果大致由2 方面引起。 一是拍摄对象与背景不在同一平面，显微拍摄金属样件表示损伤时，情况如腐蚀、碰撞凹陷使背景平面高于损伤平面，平面差的大小导致散焦模糊的程度有高低；二是在显微拍摄情况下，原本细微的震动与偏移也被等倍数地放大，并于图像生成过程中同样会被记录下来。

1.2 显微图像噪声类型

图像采集传感器容易受到电路内部结构、工作环境、相关材料固有属性、电子元器件数量等影响，从而产生各种噪声，如热噪声（电阻引起的）、光子噪声、非均匀性噪声（场效应管的沟道）［9］。 另外，例如在处理后的图像和相位分布中还存在非期望的散斑噪声。

光线在物体表面反射形成了一系列散射的子波是散斑噪声产生的主要原因。 同时，子波之间的相干性表现良好，光波相干叠加现象特别容易发生，生成了散斑噪声。 散斑极易破坏原图像的细节信息，造成图像的后续处理结果达不到预期效果，直观表现为信噪比低和图像配准率低。 Arsenault 于1976年证明了图像中的相关散斑噪声在原始图像中是以乘性噪声的形式表现的［10］。 同时，还可以知道显微图像中含有一部分的高斯噪声，如图3 所示。 图3中，红色框选为散斑噪声明显区域，蓝色框选为高斯噪声明显区域。

图3 显微图像噪声类型Fig.3 Microscopic image noise type

2 算法总体设计

根据上述图像模糊及噪声类别，提出一种改进的图像降噪模型，流程如图4 所示。 首先进行图像初步修复使用盲解卷积来针对图像的散焦模糊情况。 然后使用斑点抑制各向异性扩散滤波器［11］（Speckle Reducing Anisotropic Diffusion， SRAD）中的瞬时变化系数（ICOV）可以对斑点图像中的特征区域进行分类，SRAD 模型具有出色的斑点噪声降低和细节信息保存性能，因此在所提出的算法中，SRAD 被用作预处理滤波器。 并且从小波噪声的统计模型可以知道高斯白噪声特征的加性噪声（高斯噪声）可以在小波域中降低。 同时图像的平滑和锐化处理是一对相对的流程，为了保证图像的平滑度，又不丢失关键边缘信息，二级小波分解［12］（Discrete Wavelet Transformation， DWT）可以转换为高频子带图像和低频子带图像的父图像，进行分别处理。 保留了高频子带图像中的小波系数，使用梯度域导引图像滤波（Gradient Domain Guided Image Filtering，GDGIF）的消除高频子带图像中的主要噪声。 由于小波域中的低频子带图像包含较多的噪声，因此BM3D 被用于抑制低频子带中的噪声，同时保留边缘。 最后，使用小波逆变换重构获得降噪后图像。

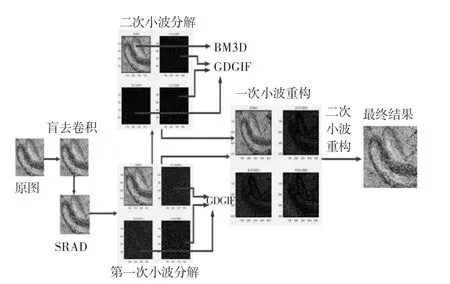
图4 算法模型流程图Fig.4 The flow chart of the algorithm model

2.1 斑点抑制各向异性扩散滤波器

斑点抑制各向异性扩散（SRAD）滤波器使用偏微分方程原理对显微图像进行降噪处理，如式（1）所示：

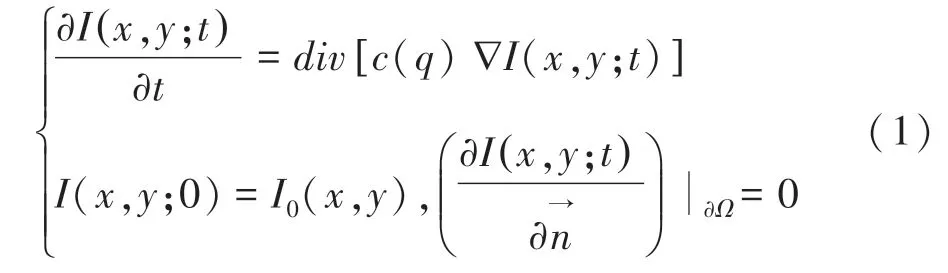
其中，I0（x，y） 和I（x，y；t） 分别表示初始图像和输出图像； ∇表示梯度算子；div表示发散算子；∂Ω表示图像Ω连续域边界；表示∂Ω的外法线向量。

式（1）中，扩散系数c（q） 决定了利用哪一种扩散方式来降低斑点噪声的影响，扩散系数计算如式（2）所示：

其中，q x，y；t( ) 和q0t( ) 分别表示瞬时变化系数（ICOV）和散斑标度的作用。 在含有散斑噪声的显微图像中，ICOV 常被作为边缘检测模型时使用，涉及到的数学表达如式（3）所示：

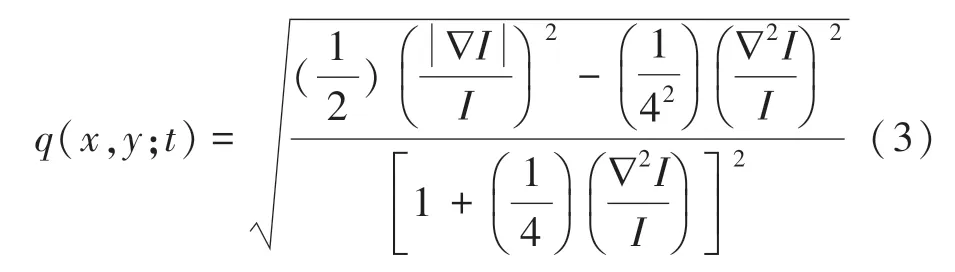
其中，∇是Laplacian 算子。 ICOV 数值在边缘区域表现为高值，而在平坦的区域则是低值。 无论是为了促进、还是抑制平滑，都可以根据图像中的区域来改变相关阈值以进行调整。 因此，该函数可以消除平滑区域的散斑噪声，同时保留边缘有效信息。根据上述功能，SRAD 滤波可直接应用于含有散斑噪声的显微图像中，以降低散斑噪声并保留特征。

2.2 离散小波分解

为了抑制显微图像中的加性噪声，这里运用了离散小波分解（DWT），即通过离散小波的方式将图像分为4 个不同的子代图像分别进行处理。 假设fi+1（x，y）∈L2(R2) ，令（j∈z） 是L2(R2) 的可分离多分辨率分析。 其中，定义的3 个二维小波，如式（4）所示：

上述3 个式子分别是L2(R2) 的正交基。

使用小波函数和尺度函数的正交特性可以进行分解，如式（5）所示：

二维MALLAT 算法滤波器的分解算法如图5所示。

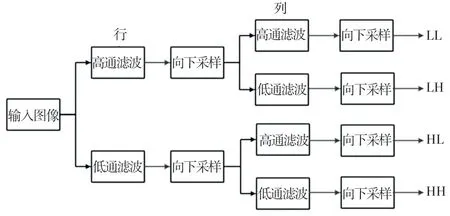
图5 小波分解原理图Fig.5 Schematic diagram of wavelet decomposition

显微图像进行三次分解，分解后图像如图6 所示。

图6 显微图像各次分解图Fig.6 Decomposition diagram of microscopic images

从理论上说，小波分解可以进行无数次，没有尽头。 但是从实际分解图可以得出显微图像中的加性噪声在第三次小波分解的高频区域中已经很少了，几乎可以忽略不计，在保证图像复原最大化的前提下，同时运算更加快捷，选用二次小波分解对显微图像进行处理。

2.3 梯度域导引图像滤波

基于添加一阶边缘感知的梯度域导引图像滤波（GDGIF），提供了很好的边缘保护和降低加性噪声的能力。 引导图像滤波（GIF）过程中最重要的假设是局部线性模型。 在制导和滤波输出之间，GIF 的损失函数定义见式（6）：

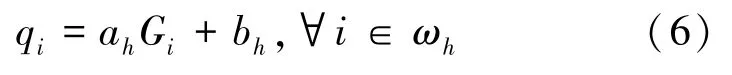
其中，(ah，bh) 是正方形窗口ωh中的线性系数，其掩码大小为h。 GDGIF 的损失函数如式（7）所示：

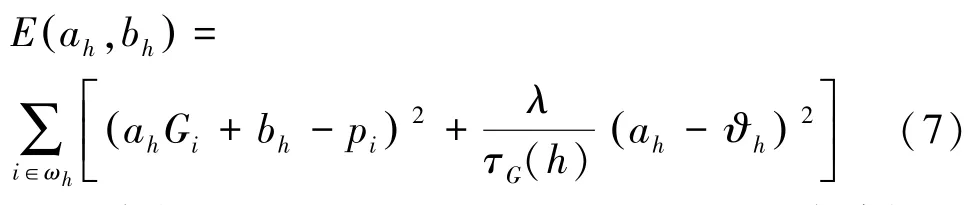
其中，τG（h） 是基于GDGIF 一阶的边缘感知权值，一阶边缘感知GDGIF 的权重如式（8）所示：

其中，τG（h）的使用依据3×3 掩模和（2h +1）×（2h +1） 窗口的局部方差来实现。ah1和bh1的优化值如式（9）、式（10）所示：

最终值如式（11）所示：

2.4 BM3D

在理想情况下，若原始图像是y，则在块匹配过程中图像块ZxR和Zx之间的距离计算如式（12）所示：

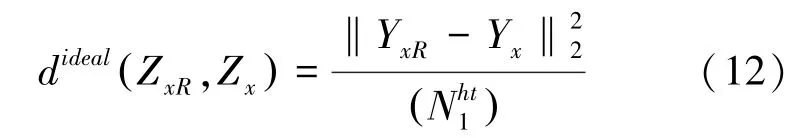
其中，xR和x分别表示2 个图像块左上角的坐标；是图像块的大小；‖.‖2是L2范数。 但实际上，理想的图像y不能直接获得，只有含噪图像可用，故按式（13）进行计算：

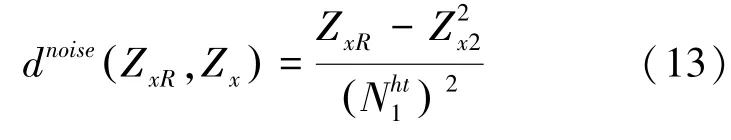
先进行二维线性变换，再进行硬阈值滤波处理使系数收缩，此时的距离如式（14）所示：

经过二维线性变换和硬阈值滤波操作，参考块的相似图像块集合可由式（15）求得：

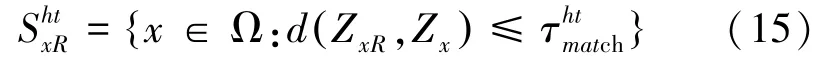
其中，是预设的阈值。 这些相似块与参照块被堆叠成为一个三维组，记作ZxR。 对三维矩阵执行硬阈值滤波操作， 再进行一维哈达玛（Hadamard）变换。 针对像素存在多个估算值的情况，重复的像素权重用公式（16）进行计算：

其中，σ2是噪声方差，是不为零元素的个数。 第一阶段的估计图像用式（17）求加权平均：

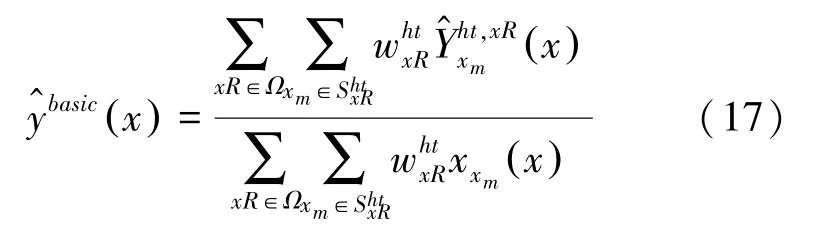
经过这一阶段处理后，图像中的噪声很大程度上已经被消除。 此后的处理同第一阶段的类似，用维纳滤波取代硬阈值滤波，数学公式如下：

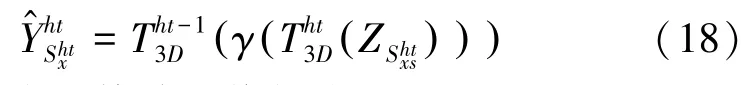
求得最终的估计图像如式（19）所示：

3 实验与分析

为了验证本文算法的优越性和鲁棒性，先选用标准图像在进行人为添加噪声的前提下，对比其处理在不同传统算法下的效果，选用峰值信噪比（Peak Signal to Noise Ratio，PSNR） 与 结 构 相 似 性（Structural Similarity，SSIM）， 这些都是有参考图像质量量化评价指标。 由于显微图像无指定标准图像，所以这里还要进行显微图像的无参考图像质量指标：图像结构清晰度（NRSS） 来进一步地验证可行性。

3.1 有无参考图像质量评价指标

PSNR［13］是最普遍，最广泛使用的评鉴画质的客观量测法，但是PSNR的分数无法和人眼看到的视觉品质完全一致，这是因为人眼的视觉对于误差的敏感度并不是绝对的，其感知结果会受到许多因素的影响而产生变化。 具体计算如公式（20）所示：

SSIM［14］是一种衡量2 幅图像相似度的指标。作为结构相似性理论的实现，结构相似度指数从图像组成的角度将结构信息定义为独立于亮度、对比度的，反映场景中物体结构的属性，并将失真建模为亮度、对比度和结构三个不同因素的组合。 计算如式（21）所示：

谢小甫等人［15］进一步改进了杨春玲等人的方法，根据结构相似度的相关思想结合人眼视觉系统的相关特点， 设计无参考图像清晰度的评价指标（NRSS），具体计算如式（22） 所示：

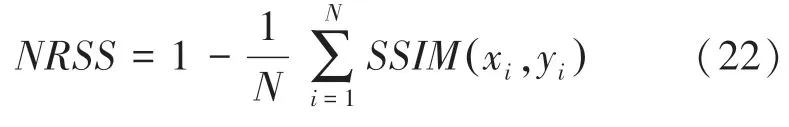
3.2 算法参数设置及结果对比

研究中，分别对2 个标准图像添加人工高斯噪声（加性）与斑点噪声（乘性），再分别通过数学形态学、中值滤波、离散余弦变换、离散小波变换、非局部均值、三维块匹配和改进算法模型进行处理，并进行量化数据对比。 相关参数设置见表1，处理结果如图7、图8 所示。

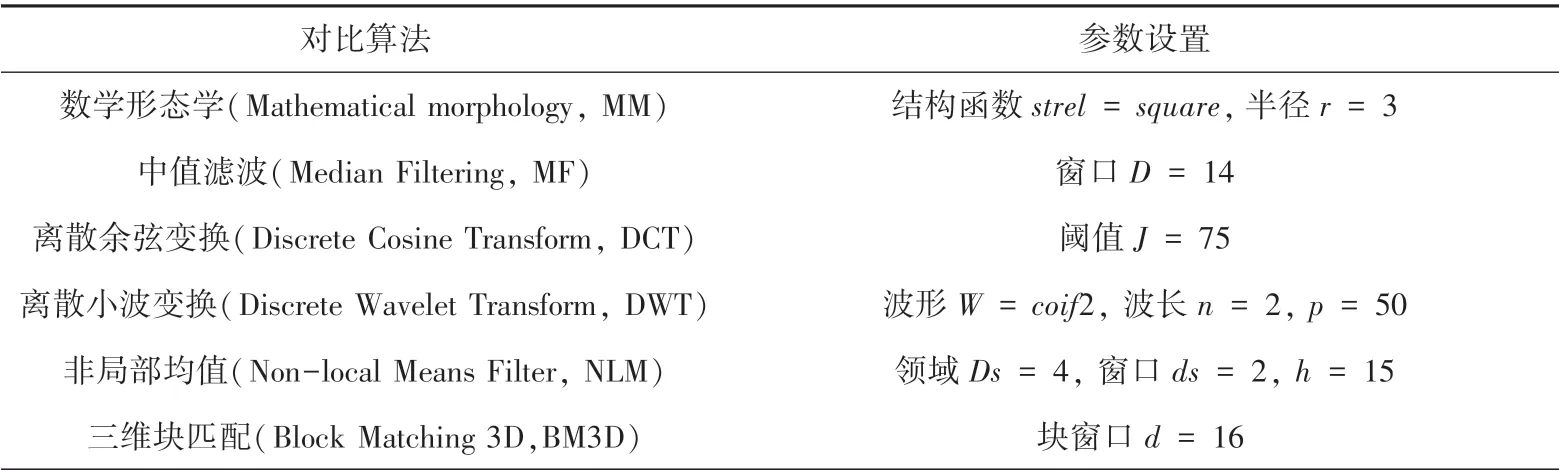
表1 对比算法具体参数设置Tab.1 Comparison of the specific parameter settings in the algorithms

图7 Barbara（低噪声）噪声图像及各算法处理结果Fig.7 Barbara （low noise） noisy image and the results of the algorithms

图8 Lenna（高噪声）噪声图像及各算法处理结果Fig.8 Lenna （high noise） noisy image and the results of the algorithms

低噪声各算法降噪量化数据对比实验结果见表2。由表2 可以得出，在图像低噪声情况下改进算法的PSNR与SSIM数值均处于最高，表现优异，虽然在个别数值上未能远远超过其他算法，但是算法鲁棒性良好。

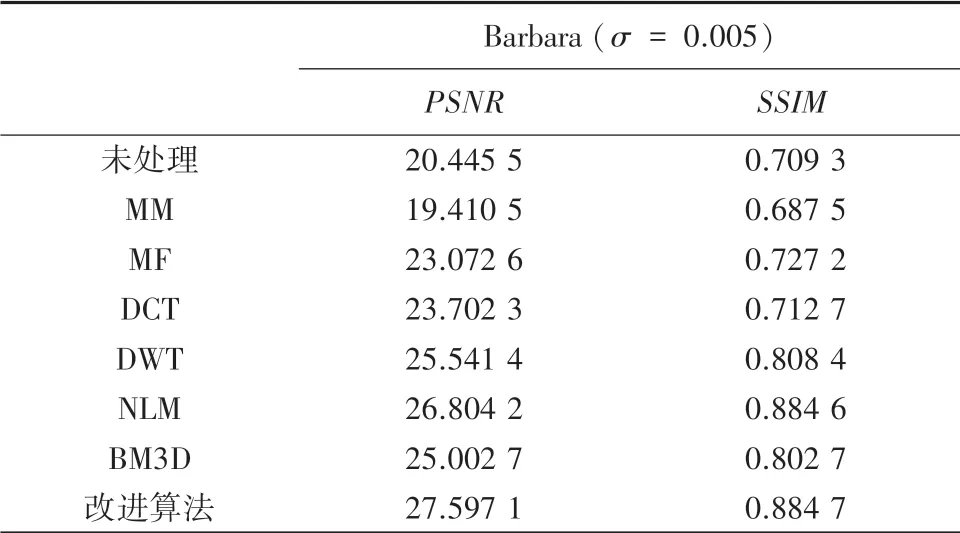
表2 低噪声各算法降噪量化数据对比Tab.2 Comparison of low-noise reduction quantized data of various algorithms

高噪声各算法降噪量化数据对比实验结果见表3。 由表3 可知， 在图像高噪声情况下改进算法的PSNR与SSIM数值均处于最高且图像结构相似性数值远远高于其他处理方法，证明该算法在高噪声情况下的优异性能。

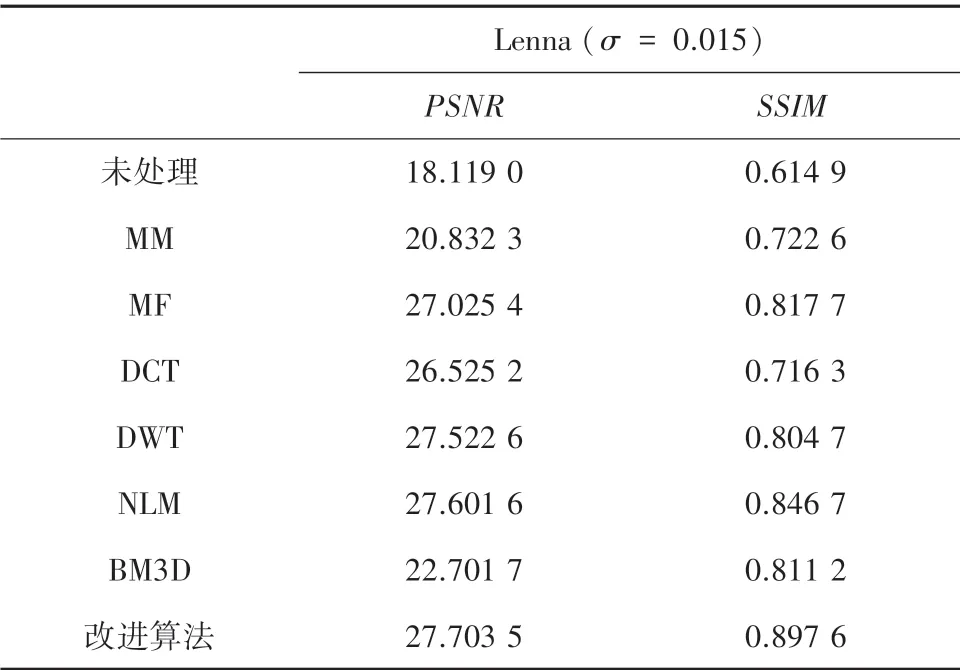
表3 高噪声各算法降噪量化数据对比Tab.3 Comparison of high-noise reduction quantized data of various algorithms

图9 为采集显微图像进行改进算法处理。 无参考显微图像评价结果见表4。 由表4 中无参考评价指标来看，处理过图像NRSS值均高于原图，表示图像结构细节更加清晰，光斑噪声也得到明显抑制。

表4 无参考显微图像评价Tab.4 No reference microscopic image evaluation

图9 显微图像原图及处理图像Fig.9 Original microscopic image and processed image

4 结束语

针对显微图像噪声及模糊类型，本文提出一种在保护边缘细节的前提下图像降噪清晰算法。 先通过盲解卷积和SRAD 去除大部分散斑噪声，在图像小波高低频图像下分别进行降噪和锐化处理，得到一个拥有丰富细节的显微图像。 实验结果表明，用该算法处理过的显微图像结构清晰度至少提高了2.5%，已知最高提升9.8%。 在其他类型图像弱噪声情况下表现出较好的效果及鲁棒性。 同时在高噪声情况下PSNR最少提升3.7 了%，SSIM最少提升了5.6%，在图像降噪领域有一定的实用价值。