基于近似条件熵的集值决策表属性约简算法
唐鹏飞
(1 四川师范大学 数学科学学院, 成都 610066; 2 四川师范大学 智能信息与量子信息研究所, 成都 610066)
0 引 言
属性约简是粗糙集理论的核心内容之一,主要是在保持相同分类能力的前提下进行冗余属性删除,从而达到数据表的优化处理[1]。 近似条件熵作为一种由近似精度与条件信息熵信息融合得到的强健度量模型,已广泛应用于不确定性测量、属性约简、机器学习。 对于经典决策表,文献[2]首先提出基于近似条件熵的属性约简;进一步,文献[3-4]将近似条件熵推广到邻域粗糙集;文献[5]利用近似条件熵进行电务设备故障预测;文献[6]分解近似条件熵,提出邻域粗糙集的特定类属性约简。 可见,近似条件熵是信息表进行属性约简的有效手段,具有重要的现实应用意义。
集值决策表是经典决策表的一种扩展,近年来已经开展了一系列相关研究。 例如,文献[7]采用条件信息熵构建集值系统属性约简。 文献[8]基于相容关系,提出信息熵、粗糙熵、知识粒度来刻画集值信息系统的不确定性。 文献[9]采用信息量构建集值信息系统属性约简。 文献[10]基于集值信息系统上的优势关系,提出多粒度优势关系粗糙集模型。 文献[11]基于相容关系,研究了一致集值决策信息系统中的属性约简和判断问题。 文献[12]针对集值数据提出2 种模糊粗糙近似,并分别构建其相对正域约简。 文献[13]从知识粒度视角,提出集值信息系统的动态属性约简算法。 文献[14]基于巴氏距离提出λ 容差关系,研究了概率集值信息系统的动态变精度粗糙集模型。 文献[15]针对集值决策信息系统中数据动态变化,构建增量式属性约简算法。 文献[16]采用正域构建集值信息系统快速约简算法。 文献[17]基于模糊相容关系,引入依赖度构建集值信息系统属性约简。 归纳可见,现有的集值决策信息系统属性约简仅从代数角度或信息角度单方面出发。 前者刻画属性对论域中确定分类子集的影响,后者刻画属性对论域中不确定分类子集的影响[18],存在局限性。
针对上述问题,本文引入近似条件熵,构建集值决策表的属性约简。 具体地,基于相容关系,将近似精度与条件信息熵信息融合建立强健的近似条件熵度量模型,挖掘度量的粒化单调性,从而自然构建基于近似条件熵的属性约简及启发算法,最后提供实例分析与实验验证。
1 集值决策表的相关知识
集值决策表SVDT ={U,AT =C∪D,V,f}。 其中,U ={x1,x2,…,xn} 为非空有限论域;C为条件属性集,D为决策属性集,C∩D =∅; 属性值域V =∪a∈ATVa,这里Va为任意属性a∈AT的值域;信息函数f:U × AT→Va, 并赋予x在属性a上的值f(x,a)∈Va。 对任意条件属性子集B⊆C,定义U上相容关系:TB ={(x,y) ∈U ×U |f(x,a) ∩f(y,a) ≠∅,∀a∈B},在TB下,对象x∈U关于B的相容类为TCB(x)={y∈U |(x,y) ∈TB},所有相容类构成一个覆盖U/TB ={TCB(x)|x∈U}。 决策属性集D在U上的划分U/TD ={D1,…,Dm},而且TD ={(x,y) ∈U ×U |f(x,D)=f(y,D)},Dh(1≤h≤m) 表示决策类。 本文用表示集合的基数。
定义1[7]决策划分U/TD关于B的条件信息熵为:
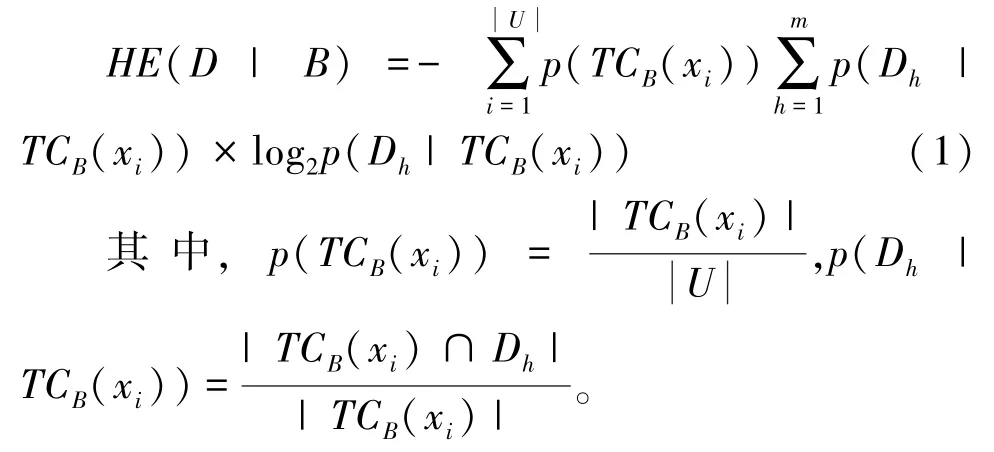
定义2[16]决策类Dh关于B的下、上近似集分别为:
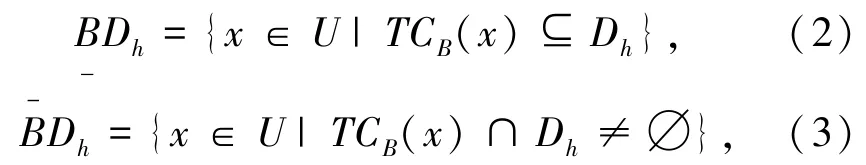
决策类Dh关于B的近似精度为:
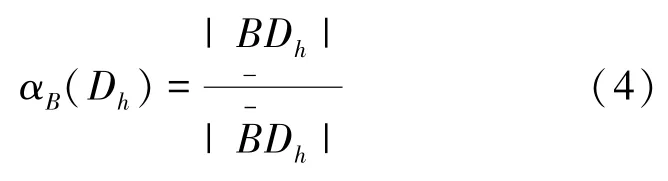
定理1[7,16]决策分析原理可表示为:
(1)B⊆C⇒αB(Dh) ≤αC(Dh);
(2)B⊆C⇒HE(D |C) ≤HE(D |B)
定义1 提供条件信息熵,其仅能刻画粒化结构的不确定性;定义2 提供近似精度,其仅能度量近似分类的不确定性[19]。 这2 种单一度量模型都存在一定的局限性。 因此,本文将两者进行信息融合,构建一种更为全面的度量模型,设计出一种更优的约简算法。
2 基于近似条件熵的启发式属性约简算法
本节在条件信息熵与近似精度基础上,构建基于近似条件熵的属性约简及其启发式约简算法,并提供实例说明算法的有效性。 为此,首先通过信息融合提出近似条件熵。
定义3决策划分U/TD关于B的近似条件熵为:

近似条件熵引入近似精度作为条件信息熵的权重系数,有效融合了两者的优点,变得更为强健。 既能度量近似分类的不确定性,又能表征粒化结构的不确定性,是一种更加全面的度量模型。
定理2B⊆C⇒AHE(D |C) ≤AHE(D |B)
证明因为B⊆C, 由定理1 可得αB(Dh) ≤αC(Dh),HE(D |C) ≤HE(D |B)。 结合定义3 可得AHE(D |C) ≤AHE(D |B)。 证毕。
推论1AHE(D |B)∈[0,|U |log2|U |]。特别地,当U/TB最细时(即∀x∈U,TCB(x)={x}),AHE(D |B) 取得最小值为0。 当U/TB最粗时(即∀x∈U,TCB(x)=U), 且决策划分最细时(即∀Dh∈U/TD,|Dh |=1),AHE(D |B) 取得最大值为|U |log2|U |。
定理2 表明,通过信息融合得到的近似条件熵仍具有粒化单调性。 进而,推论1 给出相应的值域与最值条件。 接下来,给出属性的必要性和独立性定义。
定义4∀a∈C,AHE(D |C)≠AHE(D |C -{a}),则称a为C中D必要的属性,否则称a为C中D不必要的属性。
定义5若∀a∈C为C中D必要的属性,则称C为D独立的。 由C中所有D必要的属性组成的集合,称为C中D的核,记为CoreC(D)。
基于上述近似条件熵的度量语义与粒化单调性,给出以下近似条件熵约简的定义。
定义6B⊆C为基于近似条件熵的属性约简,若能满足2 个条件:
(1)AHE(D |B)=AHE(D |C);
(2)∀a∈B,AHE(D |B -{a}) ≠AHE(D |B)
这里,属性约简模拟经典情况,主要依托近似条件熵这一核心度量及其粒化单调性。 定义6 中的2 条分别对应“联合充分性”和“个体必要性”。 特别地,近似条件熵的粒化单调性可以挖掘启发式信息;由此,下面提出对应的属性重要度,并建立启发式约简算法。
定义7B⊆C且a∈B,则a对于B关于决策划分U/TD的内属性重要度为:
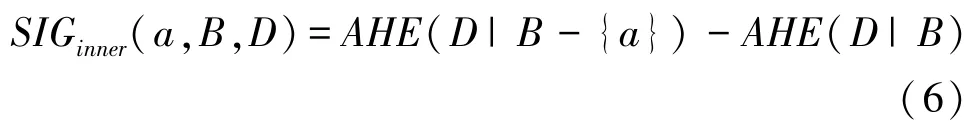
B⊆C,∀a∈C -B,则a对于B关于决策划分U/TD的外属性重要度为:
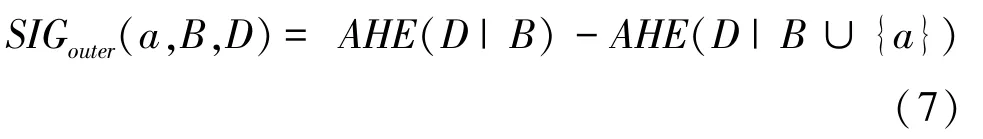
内属性重要度SIGinner(a,B,D) 刻画在B中删除属性a之后近似条件熵值的增加量,而外属性重要度SIGouter(a,B,D) 刻画在B上添加属性a之后近似条件熵值的减少量。 相关度量值变化越大,则说明该属性越重要,因此两者提供了快速约简的属性选择机制。 根据核属性概念(定义5),下面利用内属性重要度构造一个求核方法。
定理3∀a∈C,则a为C中D必要的属性⇔SIGinner(a,C,D)>0,从而,CoreC(D)={a∈C |SIGinner(a,C,D)>0} (8)
证明若a为C中D必要的属性,则AHE(D |C) ≠AHE(D |C -{a}),由近似条件熵的粒化单调性知,AHE(D |C)<AHE(D |C -{a}), 因此SIGinner(a,C,D)>0。 反之,若SIGinner(a,C,D)>0,则AHE(D | C -{a})> AHE(D | C), 从而AHE(D |C)≠AHE(D |C -{a})。 由定义4 知,a为C中D必要的属性,故式(8)成立。 证毕。
依据上述近似条件熵及约简的定义,下面以定义7 的2 种属性重要度为启发式信息,开发一个以核为约简起点的启发式约简算法,从而快速获取一个属性约简。 算法步骤具体如下。
算法1 基于近似条件熵的启发式约简算法
输入:集值决策表SVDT ={U,AT =C∪D,V,f}
输出:该区间集决策信息表的一个约简R
步骤1计算AHE(D |C)。
步骤2设置CoreC(D)=∅,∀a∈C,计算内属性重要度SIGinner(a,C,D),若SIGinner(a,C,D)>0,则CoreC(D)=CoreC(D) ∪{a},得到C中D的核CoreC(D),令R =CoreC(D)。
步骤3计算决策划分U/D关于R的近似条件熵。 若AHE(D |R)=AHE(D |C),则执行步骤5,否则执行步骤4。
步骤4∀a∈(C - R), 计算外属性重要度SIGouter(a,R,D),靠前选择外属性重要度最大的条件属性a*并入R中,即进行更新R←R∪{a*}。如果此时有AHE(D |R)>AHE(D |C),则重复该步骤选择与更新过程,直到达到条件AHE(D |R)=AHE(D |C),才执行步骤5。
步骤5向前遍历R中每个属性a,若AHE(D |R -{a})= AHE(D |R),则设置R←R -{a}。
步骤6返回R。
算法1 是以核为约简起点的启发式约简算法。步骤2 通过内属性重要度寻找到核属性集,步骤3对其进行评估,若步骤2 得到的子集R的近似条件熵大于全集C的(即AHE(D |R)>AHE(D |C)),则需进入步骤4 通过外属性重要度对剩余属性进行启发式搜索,并通过顺序选取最优属性以快速完成添加。 可见,临近步骤5 的R必然满足约简“联合充分性”,但不一定满足约简“个体必要性”。 由此,步骤5 采取后项删除过程,以确保获得“个体必要性”,从而R是一个基于近似条件熵的属性约简,最终被有效输出。
3 实例分析
本节通过一个实例,计算与分析近似条件熵性质及对应属性约简。
例1集值决策表见表1。 其中,U/TD ={D1,D2}={{x1,x2,x3,x4},{x5,x6,x7,x8}}。
基于表1,构造自然属性增链:
B1={a1}⊂B2={a1,a2}⊂B3={a1,a2,a3}⊂B4={a1,a2,a3,a4} ⊂C ={a1,a2,a3,a4,a5}。
作为例子,选取属性增链中的链元B2。 计算其诱导的相容类为:
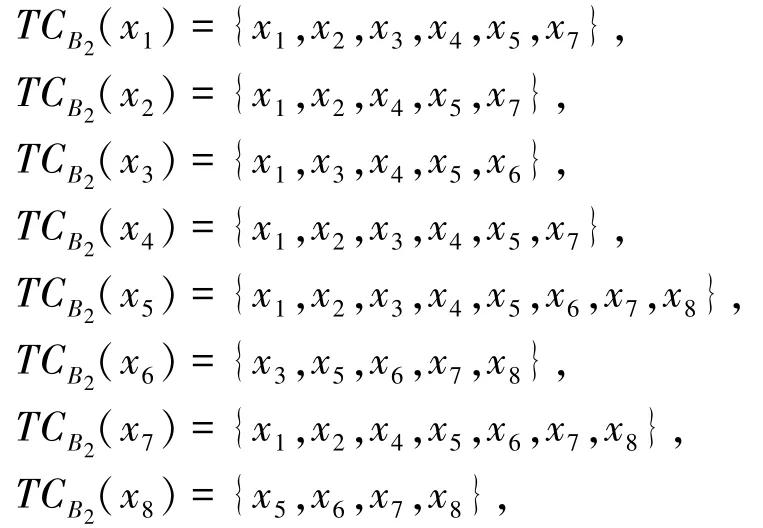
由此,可得决策类D1、D2关于B2的近似精度分别为:

下面分别计算决策类D1、D2关于B2的条件信息熵为:
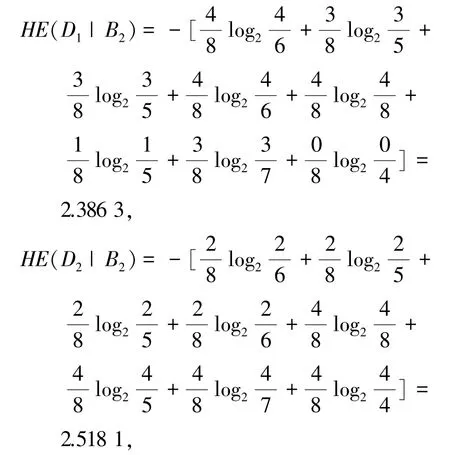
最后,计算决策划分U/TD关于B2的近似条件熵为:
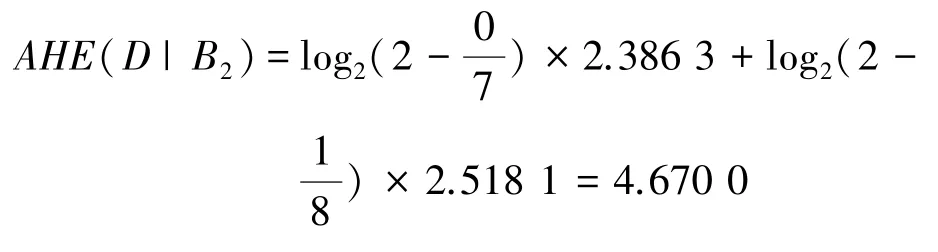
基于上述案例机制并经过类似计算,下面直接给出关于属性增链的近似条件熵及其大小关系,即:AHE(D |C)=1.617 6。
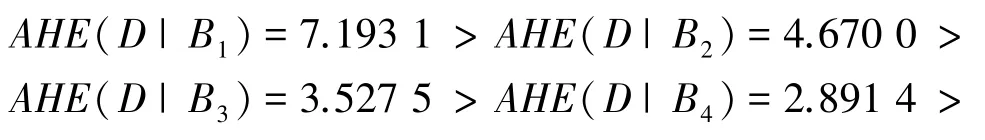
上述关于属性增链的不等式验证了近似条件熵的粒化单调性(定理2)。 所有度量值均隶属理论双界范围[0,|U |log2|U |](推论1)。
最后根据算法1 求解该集值决策表的一个属性约简。 执行步骤1,计算决策划分U/TD关于C的近似条件熵为AHE(D |C)=1.617 6。 执行步骤2,设置CoreC(D)=∅,计算C中每个属性关于决策划分U/TD的内属性重要度为:
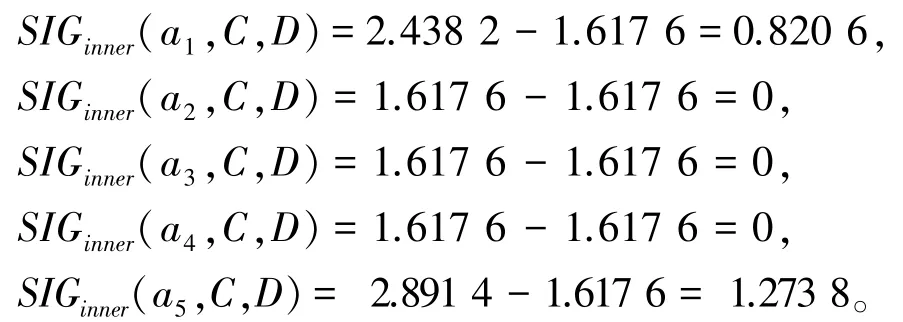
由计算可知,满足条件的属性为a1与a5, 则CoreC(D)={a1,a5}, 令R =CoreC(D)。 执行步骤3,计算决策划分U/TD关于R的近似条件熵为AHE(D |R)=3.108 6 ≠AHE(D |C)。 执行步骤4,∀a∈(C-R),计算每个属性对于R关于决策划分U/TD的外属性重要度为:
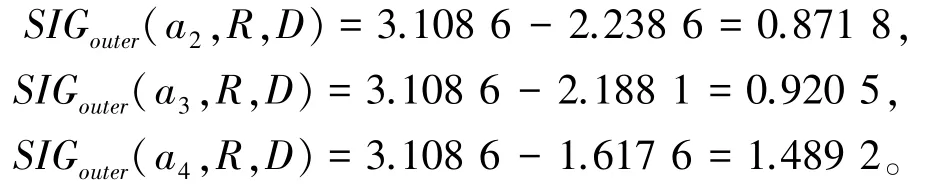
选择外属性重要度最大的属性a4并入R中,即R更新为R ={a1,a4,a5}。 计算决策划分U/TD关于R的近似条件熵为AHE(D | R)=1.617 6=AHE(D |C)。 即R满足约简第一条,所以执行步骤5,向前遍历删除R中的每个属性a,有AHE(D |R -{a}) ≠AHE(D |R),进入步骤6,返回R,即约简结果为R ={a1,a4,a5}。
4 UCI 数据实验
本节实施数据实验来验证近似条件熵及其属性约简,主要是粒化单调性(定理2)与启发式约简算法(算法1)。 将算法1 与如下信息角度和代数角度具有代表性的集值决策表启发式约简算法从约简个数与分类精度进行比较,即:基于条件信息熵约简算法[7]、基于信息量约简算法[9]和基于正域约简算法[16]。 实验环境为:操作系统Windows10 64b,Intel(R) Core(TM) i5-8200Y CPU @ 1.61 GHz,内存4.00 GB,采用Matlab2018a 进行编程实现。 下面从UCI 数据集中挑选8 组数据集,见表2。 在实验前均使用文献[16]中的方法,将UCI 数据集转化为集值决策表。
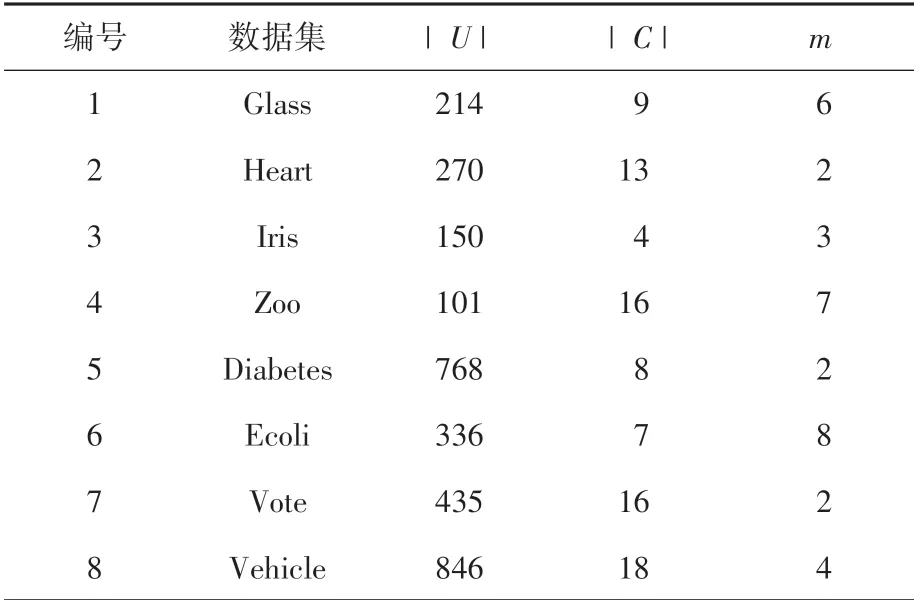
表2 数据集Tab.2 Data sets
为表现度量变化,选取自然属性增{a1} ⊂{a1,a2} ⊂…⊂C。 针对8 个数据集,分别进行了实验计算,相关度量结果见图1。 在图1 中,x轴标识属性个数,y轴标识近似条件熵度量值。 观测可见,近似条件熵值随属性个数的增加而减少,说明其具有属性粒化单调性,与定理2 一致。 基于这些单调曲线,从核出发追求与全部条件属性集近似条件熵相等的属性约简是合理的,则可以得到一个适当长度的约简结果。 下面给出8 个数据集在本文算法下的具体约简结果,见表3。 表4 则给出8 个数据集在各约简算法下的约简个数。
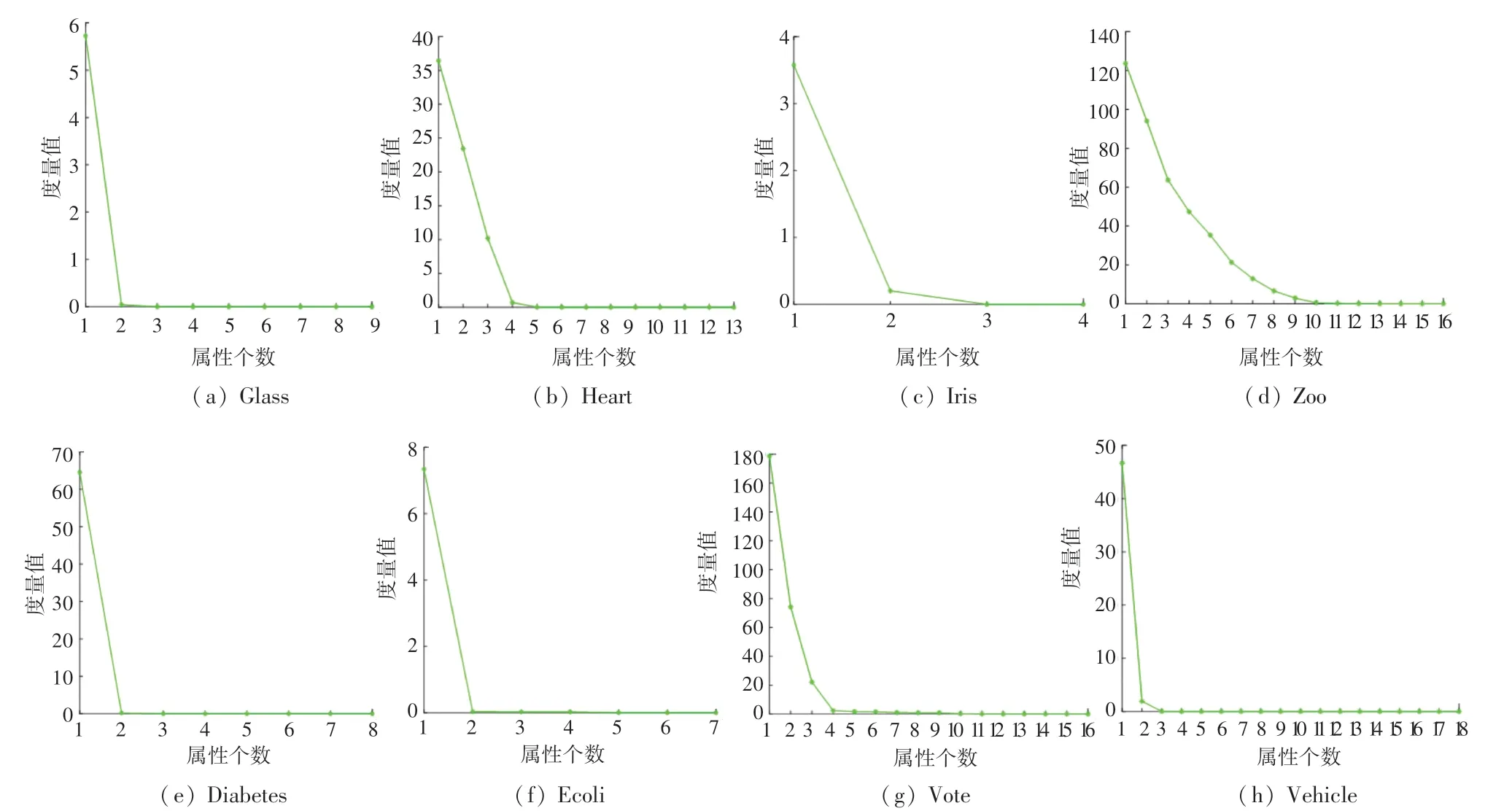
图1 8 类UCI 数据集关于属性增链的度量变化Fig.1 The measure changes of the 8 types of UCI data sets on the attribute-addition chain
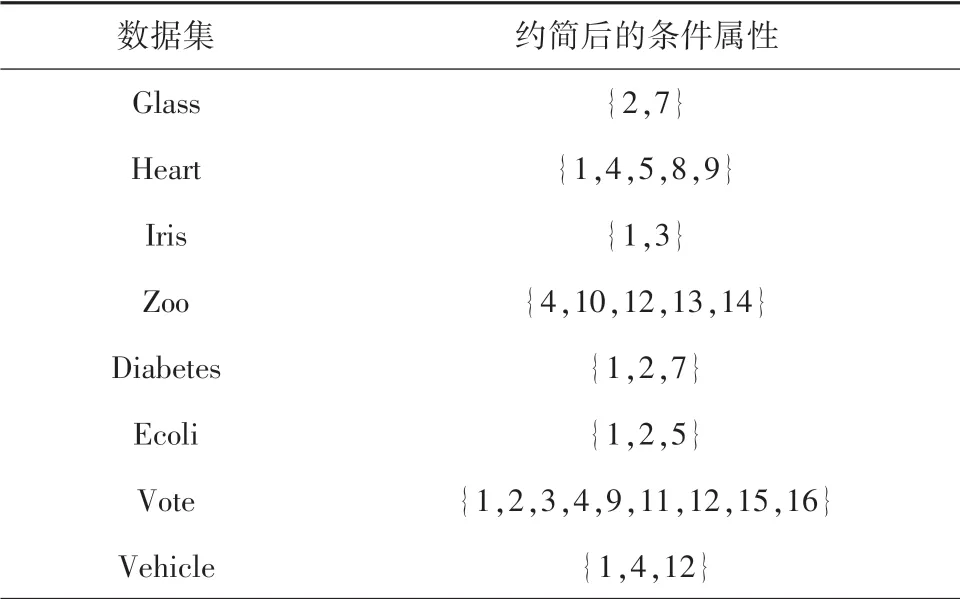
表3 本文算法的约简结果Tab.3 The reduction results of the algorithm in this paper
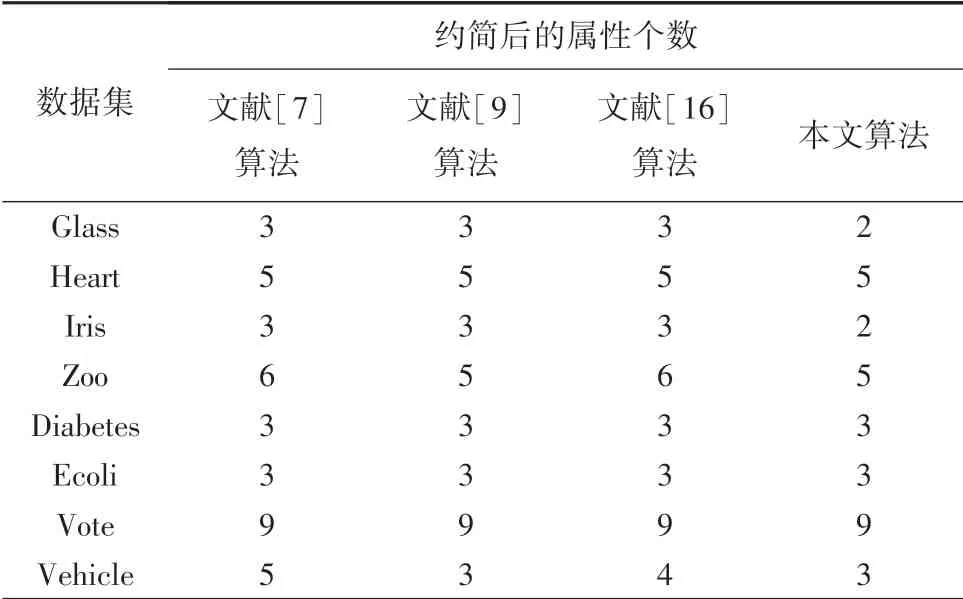
表4 不同算法的约简个数Tab.4 Number of reductions for different algorithms
由表4 可知,4 种算法约简后的属性个数都小于原始数据的属性个数,说明对数据集进行优化处理是有必要的。 比较4 种算法的约简个数,本文算法在部分数据集上约简个数更少,例如Glass、Iris、Zoo 与Vehicle 数据集;而在其余数据集上,与其它3种算法的约简个数相等。 说明本文算法的约简结果更优。
最后比较不同算法的分类精度。 这里采用SVM 分类器,对表4 中8 个数据集的约简结果进行十折交叉分类训练,得到各算法约简结果的分类精度值,具体见表5。

表5 SVM 分类器下不同算法的分类精度比较Tab.5 Comparison of classification accuracy of different algorithms under SVM classifier %
在表5 中,“√”符号标识4 种算法约简集下分类精度的最大值,“-”符号标识4 种算法约简集下分类精度持平。 观察表5 可知,本文算法在大部分数据集中,分类精度高于或等于其它3 种算法,仅在Heart、Diabetes 与Ecoli 数据集中与其它3 种算法持平。 这是因为其它3 种算法都是采用的单一度量方式,存在局限性;而本文算法采用的近似条件熵是由近似精度与条件信息熵信息融合所得,是一种更加全面的度量模型,从而具有更优的分类性能。
5 结束语
本文基于近似精度与条件信息熵,提出近似条件熵,构建基于近似条件熵的属性约简及其启发式约简算法。 通过具体实例与数据实验,验证了近似条件熵性质的正确性与约简算法的有效性,实验结果表明,本文算法不仅能够获得更优的约简结果,而且分类精度更高。 所得结果深化了信息学习与特征选择,对集值决策表的知识发现与规则推导具有意义。 下一步将对集值决策表的规则提取进行研究。此外,降低本文算法的时间复杂度,提高其运行效率,也是接下来的研究重点。

