SCARA机器人控制系统的设计与实现

李 宏，陈 平，刘宋彬

（广东工业大学 自动化学院，广州 510006）

0 引言

SCARA（Selective Compliance Assembly Robot Arm）即选择顺应性装配机械手，是一种圆柱坐标型的工业机器人，该机器人具有三个自由度，分别负责伸缩、旋转和升降运动[1]。主要应用于电子制造行业，比如IC点焊、元件贴片、货品分拣等制造当中[2]。

对SCARA机器人开展的研究集中在1）基于运动学、动力学进行数学建模分析，研究机械手轨迹规划的新方法[2～4]；2）引入新的设计方法优化机器人的控制算法，提高可靠性，抗干扰能力以及性能指标[5～7]；3）研究机器人与视觉相结合的新方法，不断优化控制精度和运动指标[1，8～9]；4）研究机器人标定的新方法，提高定标的精度和降低设计的复杂度[10，11]等。

1 SCARA机器人的运动学分析

SCARA机器人是一种平面关节机器人，具有三个旋转关节和一个垂直于平面的移动关节，其D-H参数坐标系如图1所示。其中坐标系{O0}为工作坐标系，原点O0的坐标为(0,0,0)。{O1}，{O2}，{O3}为流动坐标系，{O4}为工具坐标系。{O4}代表机器人末端执行器的位姿。参数变量θ1为机器人大臂关节角度变量，θ2为小臂关节角度变量，d3为手腕关节平移变量（d3由电机角度变量θ3通过转换得到），θ4为末端执行器的关节角度变量。连杆参数为ai=ai=li，i=1，2，3。

图1 SCARA机器人D-H参数坐标

根据矩阵变换原理及图1 SCARA机器人的结构特点，给出SCARA机器人工具坐标系与工作坐标系之间的齐次变换矩阵为

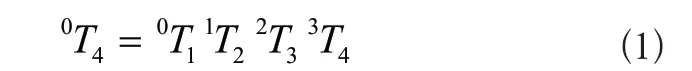
其中iTi+1，i=0，1，2，3表示坐标系{Oi+1}相对于坐标系{Oi}的位姿，其表达式分别为

其中Rot（z，θ）操作表示坐标系{Oi+1}沿坐标系{Oi}的z轴旋转θ角度，Trans（x，d）操作表示坐标系{Oi+1}沿坐标系{Oi}的x轴平移d距离，因此可得工具坐标系{O4}相对于工作坐标系{O0}的位姿矩阵为

由式(2)可得机器人末端夹具的直角空间位姿与关节角度变量的变换关系，因此可得机器人正运动学解为

其中坐标点(p x,p y,pz)为{O4}的原点相对于{O0}的空间坐标，θ为{O4}相对于{O0}的姿态。根据式(1)推导SCARA机器人反运动学解，将式(1)变换为：

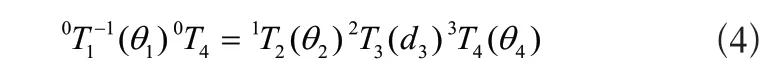
分别代入iTi+1，i=0，1，2，3的表达式，可得

在文章中，我们提出了一个安全的、可扩展的电子数据存证系统，该系统采用数据与用户对应映射关系查找来确保对电子数据池的高效访问控制。我们设计了一个基于区块链的数据存证方案，允许数据用户/所有者在身份验证后，从电子存储库访问电子数据。数据存储主要进行分片冗余算法和分布式存储保证数据安全性，并且系统引入用户积分机制，保证系统负载均衡。验证和后续服务封闭在系统内部，写入区块并成为区块链的一部分。

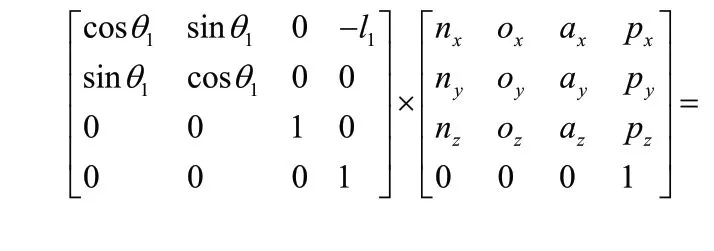
将式(5)等号两边矩阵元素一一对应，选择矩阵元素(1，4)和(2，4)联立方程组为

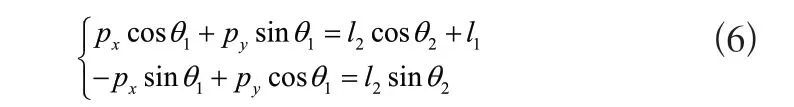
由式(6)推导可得反运动学解为

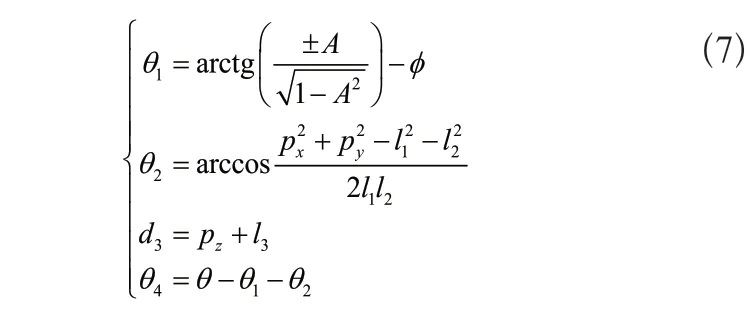
其中变量A和φ分别为

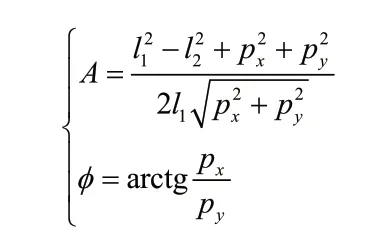
D-H参数坐标的建立，以及正反运动学的分析为SCARA机器人建立起基本的数学模型，为控制系统的算法设计提供理论基础

2 控制算法的设计与仿真

SCARA机器人一般实现两点之间的运动，根据运动形式具有点对点运动，即两点之间运动轨迹为任意曲线；另一种为直线运动，是点对点运动的特殊形式，通过插补方法可实现两点之间的直线运动。为了驱动SCARA机器人运动，将目标点位姿信息作为输入指令，控制算法根据输入指令计算得到的关节角度及角速度作为控制量输出。为了改善机器人工作指标，可选择增加路径规划算法。基于工控机+分布式控制架构的机器人控制原理如图2所示。

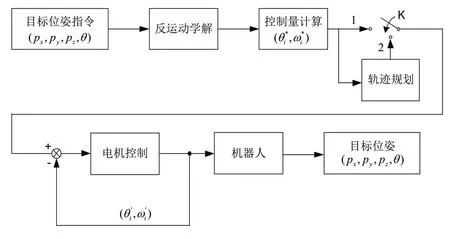
图2 SCARA机器人的基本控制原理

图2中，（px，py，pz）表示目标点的空间位置，θ表示工具坐标的姿态，输出的控制量θ*i，i=1，2，3，4表示目标位姿的四个关节角度，控制量ω*i表示四个关节的角速度，（θ'i，ω'i）分别表示四个关节角度和角速度的反馈信息，实现电机的位置和速度闭环控制。角速度计算表达式为，i=1，2，3，4，其中T为起止两点之间的运动时间，θ0i为初始位姿下的四个关节角度。

根据以上分析，在MATLAB Robotics Toolbox工具中对SCARA控制系统进行建模仿真，首先根据机器人样机参数及D-H参数法建立SCARA机器人数学模型，如表1所示。

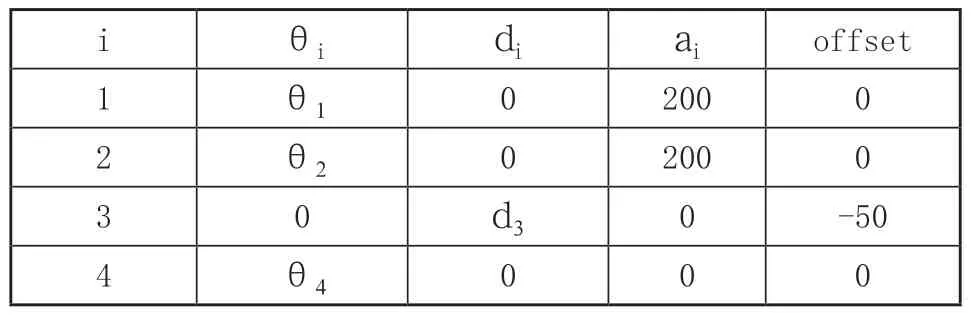
表1 SCARA机器人D-H参数表

表中i表示关节编号，θi表示变关节角度变量，ai为关节之间的连杆参数变量，大臂与小臂的连杆长度均为200mm，offset表示工具坐标{O4}原点在初始状态下的偏移量，由表1可知初始状态下{O4}的原点相对于{O0}的坐标为（0，0，-50）。SCARA机器人数学模型的程序代码如下：

其次，根据图2控制算法原理、表1的D-H参数表和式(7)设计SCARA机器人控制算法，当输入的任意空间位姿信息在机器人工作范围内，机器人能够准确到达指定位置。比如在初始位姿(400，0，-50，0)下，输入目标位姿指令(300，0，-20，45)，得到仿真结果如图3所示。

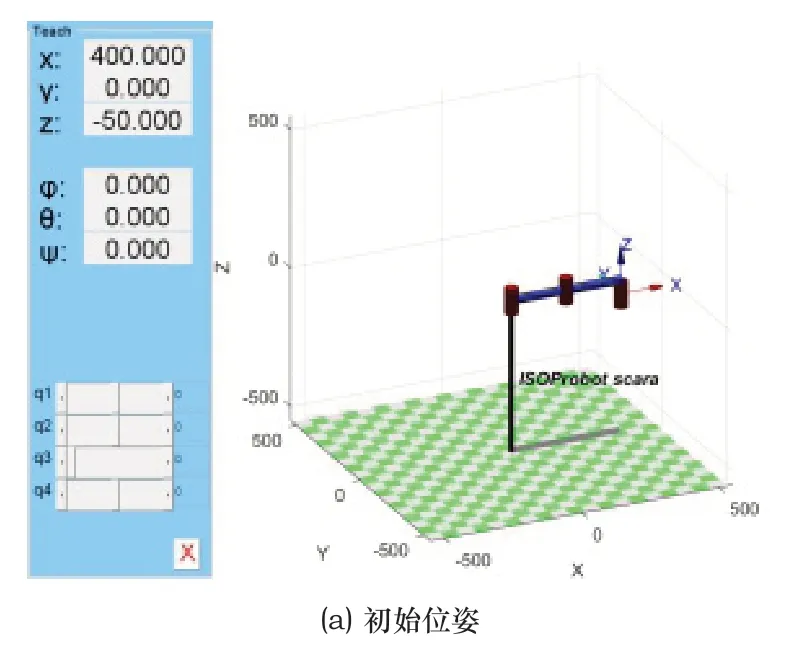
图3 机器人仿真结果

图3中，（X，Y，Z，Ψ）显示机器人的位姿信息，仿真结果表明机器人能够按照输入指令准确到达目标位姿，初步证明控制算法的可行性。

3 SCARA机器人控制系统的设计

SCARA机器人硬件平台采用工控机+分布式控制的架构，其架构原理图如图4所示。其中工控机完成运动学解、路径规划、电机信息采集，控制量输出，串口通信以及人机界面等功能；CAN站点表示驱动SCARA机器人关节的步进电机系统，步进电机系统集控制，驱动和电机本体为一体，站点之间独立工作，分别接受工控机指令并独立完成驱控操作。

图4 SCARA机器人硬件平台架构

SCARA机器人直线运动一般采用插补方法，在初始位姿（p0x，p0y，p0z，θ0）和目标位姿（p*x，p*y，p*z，θ*）之间根据要求平均插入n个插补点，可得每个插补点之间的步增距为

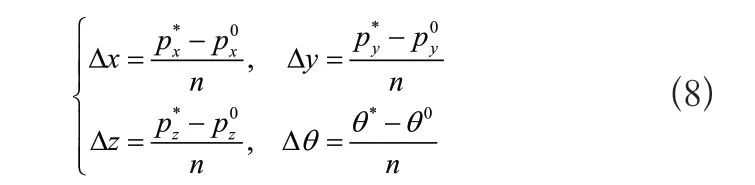
则第j个插补点的位姿为为

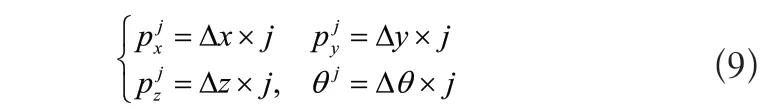
然而由于实际信道存在通信延迟，四个站点在接收指令时存在时间差，因此影响直线运动的精度。为了修正该精度误差，应将通信延迟时间纳入角速度的计算之中。假设指令传输延迟时间为σ，则按顺序站点1至站点4的通信延迟时间为λi=σ×i，i=1，2，3，4。则两个插补点之间的角速度应修正为。经过修正之后机器人能够精确经过每一个插补点，实现直线运动。机器人控制系统的软件流程图如图5所示。

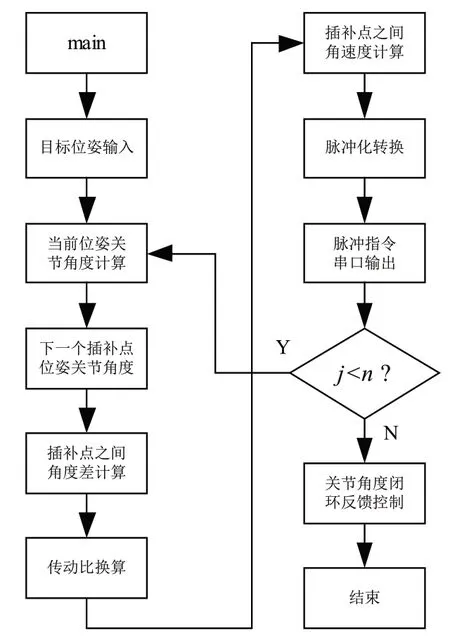
图5 SCARA机器人直线运动控制的软件流程图

在直线运动过程中，控制系统循环计算两个插补点之间的角速度，并且在下一个插补周期开始时刻更新四个关节的角速度，使得机器人能够精确经过每一个插补点位置。图5中，传动比转换模块将机械关节角度转换为电机的旋转角度；脉冲化转换模块将电机角速度转换为脉冲指令；关节角度闭环反馈控制模块将精确控制机器人准确到达目标位姿上。通过以上软件流程实现机器人直线运动控制。

4 实验测试

搭建SCARA机器人控制系统，包括：PC，USB/CAN转换器以及SCARA机器人。在PC上安装LabVIEW软件工具，利用LabVIEW设计控制算法。USB/CAN转换器连接PC以及SCARA机器人四个关节电机。四个关节电机均为步进电机驱控一体机，该系统集控制，驱动和电机本体为一体，步进电机系统之间相互独立，分别接受上位机的指令并驱动步进电机工作。SCARA机器人控制系统如图6所示。

图6 SCARA机器人控制系统实物图

在LabVIEW中设计SCARA机器人控制算法，并提供人机界面供用户输入目标位姿指令。SCARA控制系统的LabVIEW程序及人机界面如图7所示。

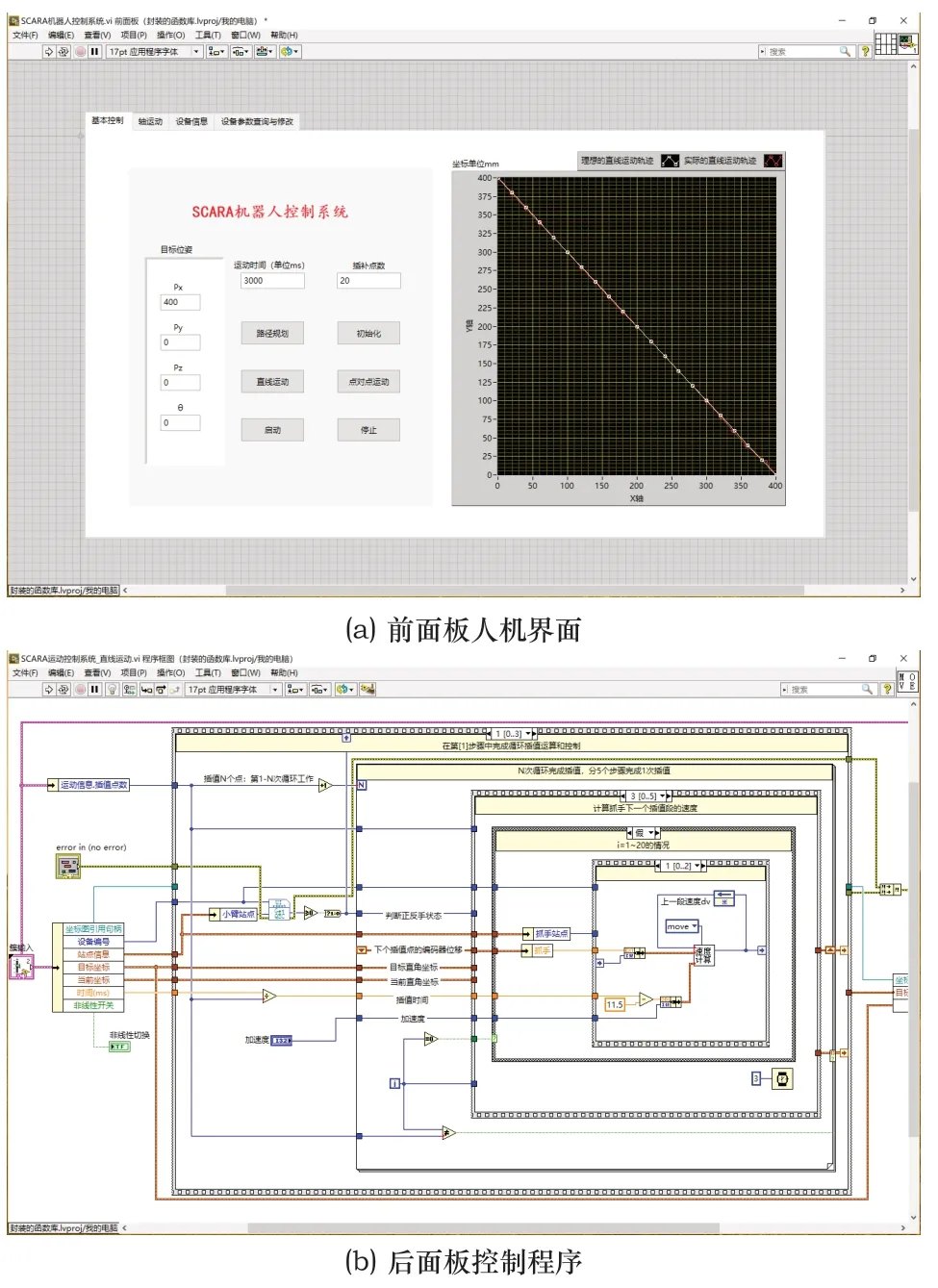
图7 SCARA机器人控制算法的软件设计图

图8中，x-y平面表示SCARA的工作平面，由图8(a)和(b)的结果对比可知，通信延迟误差修正方法能够有效解决工控机+分布式控制架构下直线运动的精度问题。图8(c)为增加轨迹规划算法，采用非线性插补方法之后得到的实验测试结果，同样具有良好的控制精度。轨迹规划算法使得机器人在启动和停止阶段具有更平滑的运动轨迹，有利于机器人的精度和稳定性。

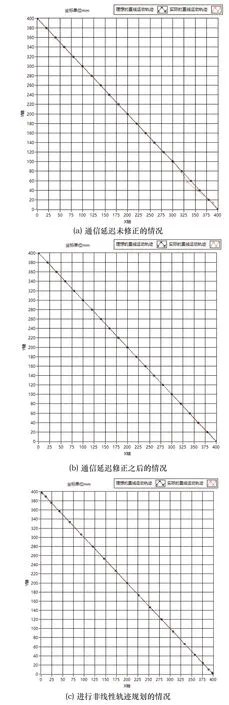
图8 SCARA机器人直线运动轨迹图

5 结语

本文主要探讨了基于工控机+分布式控制架构下SCARA机器人控制系统的设计与实现等问题。阐述了数学建模，控制算法设计，软件仿真以及硬件实现的一般过程及设计方法，实验结果表明该方法的有效性和实用性。本文的工作为下阶段的研究工作提供理论基础及技术框架。基于现有的工作基础，可进一步改善系统的性能指标，及拓展其技术内涵。