钨基辐照材料纳米氦泡诱导位错成核的分子模拟

黄鑫龙 吕陈扬韬 孙昱瑶 楚海建

(1.上海大学力学与工程科学学院, 上海 200444;2.上海大学上海市应用数学和力学研究所, 上海 200072;3.上海大学上海市能源工程力学重点实验室, 上海 200444)

核反应堆所用的结构材料往往需要承受高温、高应力、强辐照等极端服役环境[1].在聚变堆中, 氘-氚聚变产生的氦原子会引入到材料中[2].受加工工艺的影响, 金属材料中不可避免地存在一定数量的空位, 且空位相对密度随温度升高而增大[3-4].氦原子容易被材料中的空位捕获, 形成稳定的氦-空位团簇(氦泡)[5].由于热激活, 材料可以发射自间隙原子产生空位, 与游离的氦原子形成氦-空位团簇, 这个现象被称为氦的自陷[6].辐照氦泡是核反应堆结构材料的基本缺陷之一, 因此对其基本特性及其演化规律进行研究对抗辐照材料的设计与应用具有重要意义.

钨材料具有高熔点、高导热率、低储氚率等物理特性, 是核反应堆中普遍采用的抗辐照材料之一, 同时也是国际热核聚变实验堆(international thermonuclear experimental reactor,ITER)等磁约束核聚变装置中偏滤器的首选材料[2,7].Sikka 等[8]统计了823 K 高温下快中子辐照钨材料中氦泡的平均大小和密度, 氦泡直径为1∼6 nm, 平均值为3 nm.一些研究者通过电子能量损失能谱(electron energy loss spectroscopy, ELLS)、透射电镜(transmission electron microscopy, TEM)等方法间接测得氦泡内的氦密度, 通过代入氦的状态方程间接获得氦泡的内压[9].但是上述实验方法都存在一定的假设, 并需要较为复杂的理论公式进行转换, 所得的氦密度及相应内压的精度往往难以保证.再者辐照缺陷的演化, 包括氦泡诱导位错成核、生长、发射等过程难以通过实验进行观测, 因此, 分子动力学模拟成为研究辐照材料微观缺陷演化机制与规律的一种主要方法.

一般认为, 辐照氦泡的生长有两种机制: 当氦泡较小时(直径小于1 nm), 氦-空位团簇以发射间隙子并吸收氦原子的机制而长大;当氦泡较大时, 随着氦泡内吸收氦原子数量的增长, 在氦泡内产生较高的压力, 当氦泡周围的基体原子无法承受氦泡的高压时, 通过击出位错环释放氦泡压力, 并伴随氦泡体积的增长, 这个机制被称为位错环击出机制(dislocation loop-punching mechanism)[10].Trinkaus 等[11]认为小氦泡位错环击出的临界内压值随氦泡尺寸增大而减小, 而大氦泡(直径大于5.5 nm)的临界内压近似为一个常值.Xie 等[12]模拟发现:小氦泡将自间隙原子从氦泡表面推出重新排列成柱型位错环(prismatic dislocation loop), 即位错环所在的平面与伯氏矢量垂直, 进而在氦泡表面发射, 使得氦泡长大;而大氦泡(直径大于2 nm)的机理是先形成一个沿1/2<111>方向的位错, 再由其螺位错分量向相反方向交滑移, 最后将位错转变为柱型位错环.需要指出的是, 已经报道的氦泡诱导位错成核和环击现象[10,12,13], 多集中于常温条件下的模拟, 缺乏对温度效应的系统研究, 尤其对于钨基辐照材料实际工况高温条件下的研究未见报道.此外, 位错成核与发射是热激活过程, 位错成核能垒是衡量其难易程度的重要指标, 而关于这方面的研究也未见文献报道.

辐照氦泡诱导位错成核是钨基辐照材料损伤的重要机理, 本工作采用分子动力学方法系统地研究温度与氦泡尺寸对位错成核过程中氦泡极限内压的影响, 并应用微动弹性带(nudged elastic band, NEB)方法研究位错成核能垒及其实现过程, 考察氦/空位比对位错成核能垒的影响.

1 模 型

为考察钨基氦泡演化过程中的位错成核问题, 创建分子模拟模型, 模型尺寸为50a×50a×50a,a为钨的晶格常数.设置X轴、Y轴、Z轴分别沿着[100]、[010]、[001]方向, 并采用三向周期性边界.分子模拟的时间步长设置为1 fs.采用Nose-Hoover 方法控制系统温度使模型在正则系综(canonical ensemble, NVT)下弛豫160 ps 至稳定, 取最后50 ps 内的数据进行时间平均.通过常规的分子模拟, 获得0.1、300、600、900、1 200 K 下钨的晶格常数分别为0.316 52 、0.316 74、0.317 26、0.318 01、0.318 91 nm.

创建氦泡模型主要包括创建纯钨模型和在纯钨模型中引入氦泡两个步骤: ①根据不同温度下的晶格常数创建纯钨模型;②以模型中心点(0, 0, 0)处的钨原子为球心设定一个球形区域, 删除该球形区域内的钨原子, 形成孔洞(比如球形区域直径为3 nm 时, 删除893 个钨原子);③根据氦/空位比(helium/vacancy ratio, He/Vac), 即填充氦原子数与删除钨原子数之比, 在孔洞中随机填入氦原子, 形成氦泡;④在设定的温度下对模型进行弛豫.钨基材料中氦泡直径一般为几纳米[8], 本工作考察的氦泡直径为2∼5 nm.纯钨模型包含25 万个钨原子, 而含氦泡模型的原子总数随氦泡大小和氦/空位比不同而变化.

本工作采用Juslin 等[14]给出的势函数.Juslin 等[14]开发了W-He 势, 在Finnis 等[15]和Ackland 等[16]工作的基础上对W-W 势进行了改进, 同时使用了Beck[17]给出的He-He 势.该组势函数可以很好地模拟原子之间的相互作用, 并被成功地用于研究钨中氦泡表面的位错成核和生长、位错环击出、氦泡在钨表面破裂等问题[2,7,12].本工作使用美国圣地亚国家实验室开发的LAMMPS 软件进行分子模拟, 使用软件OVITO[18]对原子构型进行可视化处理.

2 结果与分析

氦泡诱导位错成核是钨基辐照材料损伤演化的重要机制.位错成核的难易程度往往可以从两个不同角度进行分析: 一是基于氦泡内压驱动, 直接生成位错[10-11];二是基于热激活思想,分析位错成核所需克服的能垒.下面就从这两个角度分别进行研究, 主要包括: ①模拟位错环击出过程, 分析成核过程基本特征;②研究温度和氦泡尺寸对位错成核过程中氦泡临界内压的影响;③研究氦泡内压或氦/空位比对位错成核能垒的影响.

2.1 氦泡诱导位错环击出机制的模拟

图1 给出了位错环击出过程在不同模拟时刻的原子构型图, 模型中氦泡孔径为2 nm,氦/空位比为3.97, 模拟温度为300 K.钨单晶为体心立方体(body-centered cubic, BCC)结构,距离氦泡与位错稍远的钨原子均为BCC 晶格原子, 为了便于观察位错成核过程, 图中仅显示了非BCC 结构的原子.图1 为0、110、130、143、144、145 ps 模拟时刻基于近邻原子分析(common neighbor analysis, CNA)[19]的原子构型视图, 其中颜色表征原子到氦泡球心的直线距离.图1(g)∼(i)为基于位错提取算法(dislocation extraction algorithm, DXA)[20]的构型视图, 其中绿色线条为1/2<111>位错.图1(a)为初始构型, 在300 K 下弛豫110 ps 后, 氦泡表面沿{110}面滑移生成一条1/2<111>位错(见图1(b)), 随着模拟时间的增加, 该位错逐渐扩展并形成一个闭合的位错环, 最终该位错环演化为一个柱型位错环, 并沿<111>方向击出, 远离氦泡(见图1(f)).上述位错环击出过程与Xie 等[12]发现的过程基本一致, 表明本工作中的势函数和模型可以很好地模拟由氦泡内压诱导生成并击出位错环的整个过程, 为后续研究提供基础.需要指出, 位错成核与氦泡内压有重要关联, 是否能够产生位错将在下一节中分析.

图1 位错环击出过程的分子动力学模拟Fig.1 Molecular dynamics simulation of dislocation loop-punching process

2.2 氦泡的极限内压及其温度效应

氦泡极限内压是指在氦泡周围位错从无到有过程中, 氦-钨界面所能承受的最大内压值,而极限氦/空位比就是极限内压所对应的氦/空位比.图2 为不同温度下氦泡内压随氦/空位比变化的规律, 模型中氦泡直径为3 nm.由图2(a)可知: ①在同一温度下, 存在一个极限氦/空位比, 当氦/空位比小于极限氦/空位比时, 氦泡内压随氦/空位比的增大而增大, 且基本呈线性关系;②当氦/空位比大于极限氦/空位比时, 氦泡内压并不随氦/空位比的增加而增加, 这主要是由于过高的氦/空位比引起过高的氦泡内压, 位错环击出机制被激发(见图1), 导致氦泡体积的增大, 从而有效地释放了氦泡内压.以室温300 K 下孔径为3 nm 的氦泡为例, 氦泡的极限氦/空位比为3.4∼3.5.重新建立模型, 分析氦/空位比为3.41∼3.49 时氦泡内压和原子构型时发现: 氦/空位比为3.48 时, 氦泡内压为33.7 GPa, 氦泡附近无位错产生;氦/空位比为3.49 时, 氦泡内压为25.9 GPa, 氦泡附近产生了一条1/2<111>位错.因此, 室温300 K 下孔径为3 nm 的氦泡的极限内压为∼33.7 GPa, 极限氦/空位比为∼3.48.另外, 由图2(b)可知,氦泡极限内压随着温度升高而减小, 当温度升高到1 200 K 时, 极限内压由常温时的33.7 GPa 降为26.0 GPa.

Wolfer[10]提出了位错成核所对应内压的理论公式,

式中:γ、µ和b分别为材料的表面能、剪切模量和位错伯氏矢量模;r为氦泡半径.晶体材料中, 不同晶面往往具有不同的表面能.为此, 分别计算300、600、900、1 200 K 下单晶钨(100)、(110)、(111)、(211)面的表面能, 其平均值分别为3.299、3.278、3.267、3.224 J·m−2.BCC 钨晶体材料中1/2<111>位错的伯氏矢量模为/2.材料的剪切模量与温度和压强有关, 根据Steinberg 等[21]提出的SCG(Steinberg-Cochran-Guinan)本构模型, Peng 等[22]给出了钨材料剪切模量的计算公式,

式中:T为温度;P为外部载荷的压强;G0= 160 GPa (参考态的剪切模量, 温度为300 K, 压强为0);压强系数G′P/G0= 9.4TPa−1, 温度系数G′T/G0=−0.14×10−3K−1;压缩比η=V0/V.设无外部压力(P=0), 由式(2)计算可得300、600、900、1 200 K 下钨的剪切模量分别为160.00、153.28、146.56、139.84 GPa.

将上述表面能、晶格常数和剪切模量代入式(1), 可求得不同温度下氦泡极限内压的理论值.将该理论值与模拟分析所得的结果进行比较, 结果如图2(b)所示.由图2(b)可知: 在总体趋势上, 理论值与模拟值是一致的, 随着温度的升高, 二者所对应的极限内压值呈明显的下降趋势;300 K 时氦泡极限内压的模拟值与理论值相差很小, 可以忽略;但随着温度的升高, 两者的差异性逐步增大, 当温度达到1 200 K 时, 相对误差为15.56%.产生这一误差的主要原因可能源于理论模型的过于理想化, 如将氦泡当作完美的球体(实际为多面体), 忽略不同晶面表面能的差异性, 以及位错成核过程弹性场的复杂性等.

2.3 氦泡的尺寸效应

图3(a)为300 K 时不同尺寸氦泡的内压随氦/空位比的变化规律.由图3(a)可知: ①当氦/空位比小于极限值时, 氦泡内压随着氦/空位比的升高而升高, 近似为线性关系, 而当氦/空位比超过极限值时, 氦泡内压不升反降;②氦泡极限内压呈现明显的尺度效应, 即氦泡越小,其所能承受的极限内压越高, 如当氦泡直径为2 nm 时, 模拟获得的极限内压为∼41.3 GPa, 远高于3 nm 时的极限内压(∼33.7 GPa).将模拟极限值与式(1)预测的理论值进行了比较(见图3(b)), 可以发现: ①二者在趋势上是一致的, 即随着氦泡直径增大, 极限内压减小, 因此式(1)能够定性地反应尺寸效应;②在氦泡直径为3 nm 时, 理论值与模拟值符合得很好, 而当氦泡直径小于3 nm 时, 理论值高于模拟值(氦泡直径2 nm 时的相对误差为22.2%), 当氦泡直径超过3 nm 时, 理论值低于模拟值(氦泡直径4、5 nm 时的相对误差分别为14.4%、22.5%).尽管在考虑温度效应与尺寸效应时, 式(1)存在较大的误差, 但从工程应用或估算的角度来看,考虑到位错成核过程的复杂性, 包括缺陷氦泡的多面体特性、位错成核引起的复杂弹性场以及热扰动等因素, 式(1)不失为一种快速估算位错成核临界内压的有效途径.

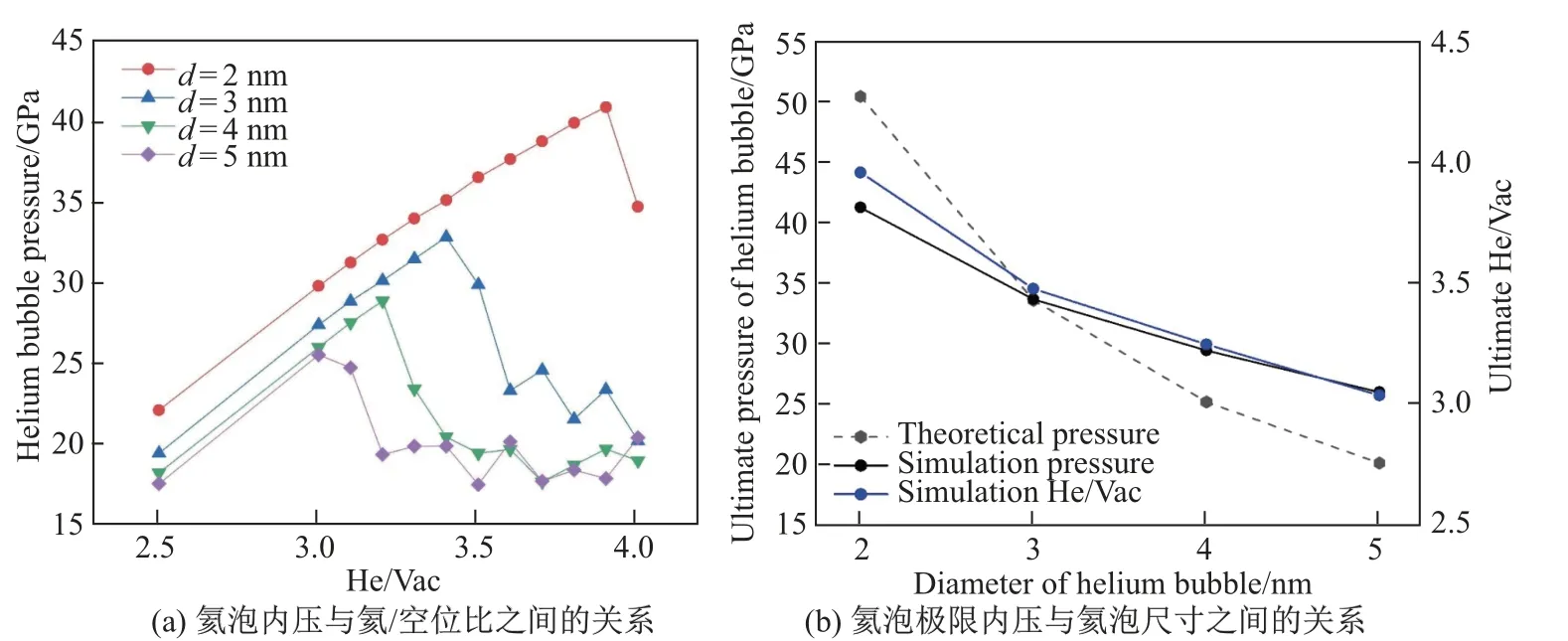
图3 300 K 时氦泡尺寸与氦/空位比对氦泡内压的影响Fig.3 Effect of bubble size and He/Vac on pressure of the helium bubble at 300 K

2.4 氦/空位比对位错成核能垒的影响

采用NEB 方法计算氦泡诱导位错成核能垒需要构建两个原子构型: 初始构型S 和最终构型F.创建初始构型与最终构型过程如下: ①采用本工作中的方法创建含直径3 nm 孔洞的模型, 设为模型S0;②在模型S0 的孔洞内填充足够多的氦原子(氦/空位比为3.49), 并在300 K 下弛豫, 通过内压自发产生附着在氦泡上的位错;③删除模型内的氦原子, 得到新的模型F0;④在模型S0 的孔洞内随机填充所需考察的氦原子数(氦/空位比为2.60∼3.40), 并根据0.1 K 时的晶格常数调整模型尺寸, 设置模拟温度为0.1 K, 在正则系综下弛豫, 获得含一定氦/空位比的初始构型S;⑤根据初始构型S 中每一个氦原子的ID 和坐标位置, 在模型F0 中填入相同ID 和坐标位置的氦原子, 并将模型尺寸设置为与初始构型同样的大小, 模拟温度设为0.1 K, 并在正则系综下弛豫, 获得含相同氦/空位比的最终构型F(构型F 包含一条附着在氦-钨界面上的1/2<111>位错, 模拟显示该位错没有被氦泡吸收湮灭).上述弛豫过程设为周期性边界条件.

图4 为氦/空位比对氦泡周围位错成核能垒的影响.图4(a)给出了不同氦/空位比条件下从初始构型到最终构型的最低能量路径(minimum energy path, MEP)上各中间构型与初始构型之间的能量差, 相应能垒的计算结果见图4(b).反应坐标(reaction coordinate,RC)代表不同构型在MEP 上的坐标,Rc为0 代表初始构型,Rc为1.0 代表最终构型, 中间构型的Rc为0∼1.0,Rc越接近1.0 代表构型的原子分布越接近最终构型.正向能垒(forward energy barrier)是指从初始构型到最终构型需要跨越的能垒, 而反向能垒(backward energy barrier)指从最终构型到初始构型需要跨越的能垒.由图4(b)可知: ①位错成核的正向能垒随氦/空位比的增加而单调递减, 而位错湮灭所需的反向能垒随氦/空位比增大而增大, 表明氦/空位比的增加有利于位错的成核, 这与图2(a)和图3(a)的结果相一致;②正向能垒曲线与反向能垒曲线存在一个交点, 其对应的氦/空位比为3.02(采用线性插值方法获得), 称为等能垒氦/空位比.交点位错成核所需克服的能垒与位错湮灭所需克服的能垒相同, 从热激活的角度来看, 二者相等表明: 在此氦/空位比下, 位错的成核概率与湮灭概率相当.在该交点的左侧, 即氦/空位比小于3.02 时, 正向能垒大于反向能垒, 表明位错成核要比位错湮灭跨越更高的能垒, 即使通过热激活产生位错, 也有更大的概率湮灭;而在该交点的右侧, 情况正好相反, 一旦通过热激活产生位错, 该位错则有较大的概率稳定存在.图4(b)还表明, 存在位错成核能垒大于0, 但初始构型能量高于最终构型能量的情形, 如图4(a)中填充比为3.2 时的情形(紫色曲线).在此情形下, 只要有足够高温度和时间, 位错成核就能够发生.而采用氦泡内压直接驱动位错成核时, 当正向能垒大于0 时, 受限于模拟时间的限制(通常为皮秒量级), 往往难以模拟出位错成核现象, 为了观察到位错成核现象, 必须增加氦/空位比, 因此模拟获得的极限氦/空位比高于实际位错成核所需的氦/空位比.

图5 为最低能量路径上典型的中间构型, 其中氦泡的直径为3 nm, 氦/空位比为3.图5(a)∼(e)中仅显示了非BCC 结构的原子, 颜色代表原子到氦泡球心的直线距离, 图5(f)-(j)为DXA 视图, 其中绿色代表1/2<111>位错, 紫色代表<100>位错.由图5 可知, 位错成核过程主要包括: ①在氦泡与钨原子交界处会产生位错胚胎(见图5(a)和(f));②该位错胚胎发展成为一条<100>位错和一条1/2<111>位错(见图5(b)和(g));③<100>位错与1/2<111>位错相互竞争, 前者不断扩展形成一条较大的<100>位错, 而后者被氦泡吸收而湮灭(见图5(c)和(h));④在邻近<100>位错附近出现一新的1/2<111>位错, 该位错与<100>位错竞争, 并进行位错反应(见图5(d)和(i));⑤通过不断的滑移与位错反应, 最终形成一条1/2<111>位错(见图5(e)和(j)).相应的位错反应公式为

图5 氦泡诱导位错成核最低能量路径上典型的中间构型Fig.5 Typical intermediate configurations on the minimum energy path of dislocation nucleation induced by helium bubble

将NEB 计算获得的位错成核过程所对应的中间构型与300 K 下由氦泡内压直接驱动位错成核的过程进行比较(同为3 nm 情形), 两者的典型特征是一致的, 即都出现了1/2<111>位错与<100>位错的竞争, 且都存在式(3)的位错反应, 并最终生成1/2<111>位错.因此, 两种不同方法获得的成核过程可以相互印证.

3 结束语

本工作从氦泡内压直接驱动位错成核和NEB 方法分析成核能垒两个角度, 模拟分析了温度、尺寸以及氦/空位比等因素对钨基辐照材料中氦泡诱导位错成核过程的影响.

(1) 采用分子动力学方法模拟了氦泡内压驱动位错环击出的整个过程, 通过NEB方法详细分析了位错成核过程, 形成了氦泡诱导位错成核、位错环形成、位错环发射的完整链条.

(2) 从氦泡内压驱动位错成核的角度来看, 存在一个极限氦/空位比, 当氦/空位比超过该极限值时, 在氦-钨界面上位错成核并扩展.极限氦/空位比对应的极限内压呈现出明显的温度效应和尺寸效应, 即极限内压随着温度和氦泡尺寸的増大而减小.因此, 无论是温度的升高,还是氦泡长大, 都导致材料的加速损伤, 对保持钨基辐照材料的性能产生不利影响.

(3) 从位错成核能垒的角度来看, 氦/空位比的增加可以有效地降低位错成核所需的能垒,从而有利于位错成核以及氦泡的生长.热激活在位错成核与扩展中起到重要作用, 位错成核与位错湮灭是两个相互竞争的过程, 一般来说, 当成核能垒大于湮灭能垒时, 位错成核的概率要高于湮灭的概率.需要指出, 内压驱动分析得到的极限氦/空位比和能垒分析得到的等能垒氦/空位比在数值上并不一致, 前者要比后者高.前者表明在此氦/空位比下通过分子模拟必定能够产生位错, 而后者表示在此氦/空位比下, 位错成核与位错湮灭的能垒相等, 具体能否跨越能垒生成或湮灭位错, 取决于温度以及其他外界因素.因此, 两者并不矛盾.

比较来看, 由氦泡内压直接驱动生成位错与采用NEB 方法进行能垒分析, 两种方法在分析问题时各有优缺点: 前者更加直观, 有利于整个位错环击出过程的总体考察, 但所得结果受限于模拟时间, 可能引起不同的解读;后者侧重于不同状态间最低能量路径的寻优, 但获得能垒后, 并不能直接得出位错成核的临界条件.两者结合使用, 相互印证, 可使得对问题的理解更加深入.另外, 本研究的结果和采用的方法可为钨基辐照材料损伤演化研究提供有益的参考.