各种对称性下挠曲电系数的Kronecker 张量积表示

吁鹏飞 彭黎明 冷伟丰 锁要红

(1.福州大学机械工程及自动化学院, 福建 福州 350108;2.西安交通大学航天学院, 机械结构强度与振动国家重点实验室, 陕西 西安 710049)

不同于压电效应与电致伸缩效应, 挠曲电效应是一种新型的力电耦合效应.挠曲电效应的宏观具体表现为: 晶体中的应变梯度会使晶体产生电极化, 即正挠曲电效应;反之, 晶体中的极化梯度也会在晶体内部产生应力和应变, 即逆挠曲电效应.Kogan[1]首先给出了正逆挠曲电效应的唯象学描述:

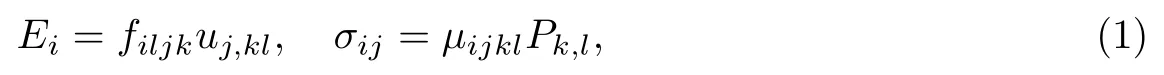
式中:σ、E、P、u分别为柯西应力、电场强度、电极化和位移;f和µ分别是正挠曲电系数和逆挠曲电系数.压电系数为三阶张量, 只能存在于非中心对称材料中;挠曲电系数为四阶张量, 在任何材料中都存在, 这极大地拓宽了力电转换器件的材料选择范围.此后, 人们分别从理论[2-3]、分子动力学模拟[4-5]、实验测量[6-7]和器件应用[8-9]等方面对挠曲电效应开展研究.

上述研究均是建立在正确的挠曲电系数基础上的, 比如不同晶体点群挠曲电系数的对称性及具体的分量.Cross[10]认为挠曲电系数与电致伸缩系数具有相同的对称性.Le 等[10]基于Cartan 分解推导了挠曲电张量对称点群的种类和相应的个数.基于高阶张量的正交不可约分解和偏张量的多极表示, 唐昌新[12]对挠曲电张量进行了对称分类并分析了独立分量的个数.文献[11-12]都只是给出了不同点群独立挠曲电系数分量的个数, 并没有给出挠曲电系数具体的分量.Shu 等[13]利用18×18 的正交变换矩阵得到了各种晶体点群下挠曲电系数的对称分量及独立分量个数.文献[12-13]系统地总结了不同晶体点群下挠曲电系数独立个数及相应的矩阵形式, 为挠曲电领域的其他研究夯实了基础.此后关于挠曲电系数对称性的研究工作急剧减少, 直到2018 年, Eliseev 等[14]认为挠曲电系数还存在着隐藏的对称性, 这将大大减少挠曲电系数的独立分量个数, 该工作对挠曲电系数对称性的研究注入了新的活力.研究表明: 在某些晶体点群下, 通过正交变换矩阵得到的系数矩阵并不正确.基于此, 本工作采用Kronecker张量积法分析不同点群下挠曲电系数的对称性.

Kronecker 张量积(层积)是张量之间的一种直积, 且正交旋转张量的Kronecker 张量积在对称性方面有着重要的作用[15].郑泉水等[16]利用张量层积理论分析了弹性张量和微极弹性张量的对称性.宋固全等[17]利用Kronecker 张量积分析了不同材料二次弹性张量的对称种类、独立分量个数和矩阵结构形式.

不同于繁杂的正交变换矩阵, 本工作用张量层积理论推导挠曲电张量空间上正交旋转张量的4 次Kronecker 张量层积, 并分析讨论了7 大晶系、32 个晶体点群及各向同性材料的挠曲电张量的独立分量个数和具体矩阵结构形式.

1 预备知识

由于只有Lifshitz 不变量fijkl(εijPk,l −Piuj,kl)和能量相关, 正逆挠曲电系数满足关系f=−µ.因此, 正逆挠曲电系数满足同样的对称性质, 二者研究其一即可.本工作以挠曲电系数µ为研究对象, 它满足性质

式中:µijkl=µ·(eiejekel), (ei,i=1,2,3) 是三维空间中的一组标准正交基.具有上述对称性质的四阶张量称之为挠曲电张量空间, 记作F, 且dimF=54.

根据Neumann 对称性原理, 挠曲电系数的对称性是指:给定材料任意一个对称变换Q, 该材料的四阶挠曲电系数µ都必须满足

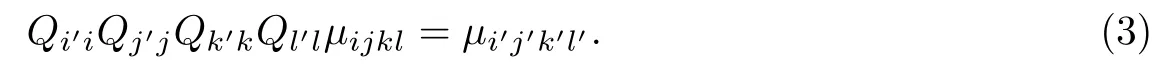
依据文献[15], 式(3)可以采用对称变换张量Q的4 次Kronecker 幂改写为

Kronecker 张量积的重要性质有

式中:α1,α2,··· ,αp分别是L对应特征根λ1,λ2,··· ,λp的特征矢量;α1α2···αp是p个矢量的并积.结合式(4)和(5)可知,µ的对称性是指:µ必须是正交变换Q⊕4对应特征值为1 的特征张量.

设三维二阶张量空间的标准正交基为

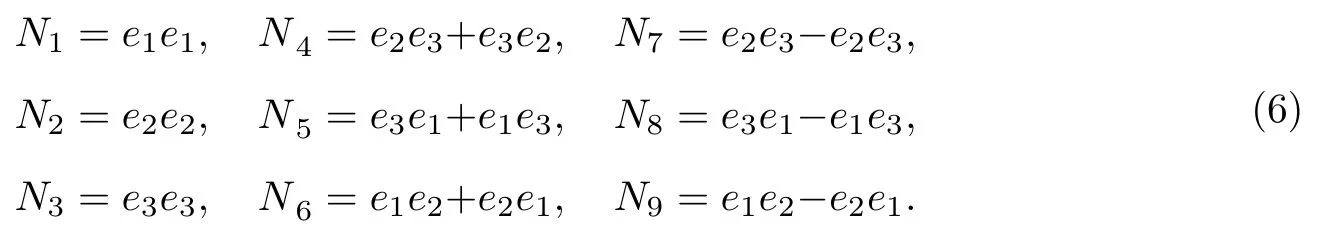
三维二阶对称张量空间的标准基为

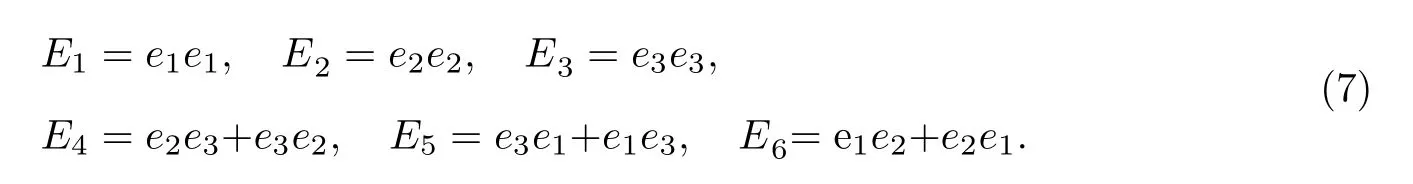
假设Q是绕e3轴转动θ角的转动张量, 即

式中:I是单位矩阵.经过推导, 满足F上的正交变换Q和Q⊕4的特征值和相对应的特征张量见表1.表1 中从上到下、从左到右的顺序, 记Q⊕4中54 个特征值为则挠曲电系数µ可以写为

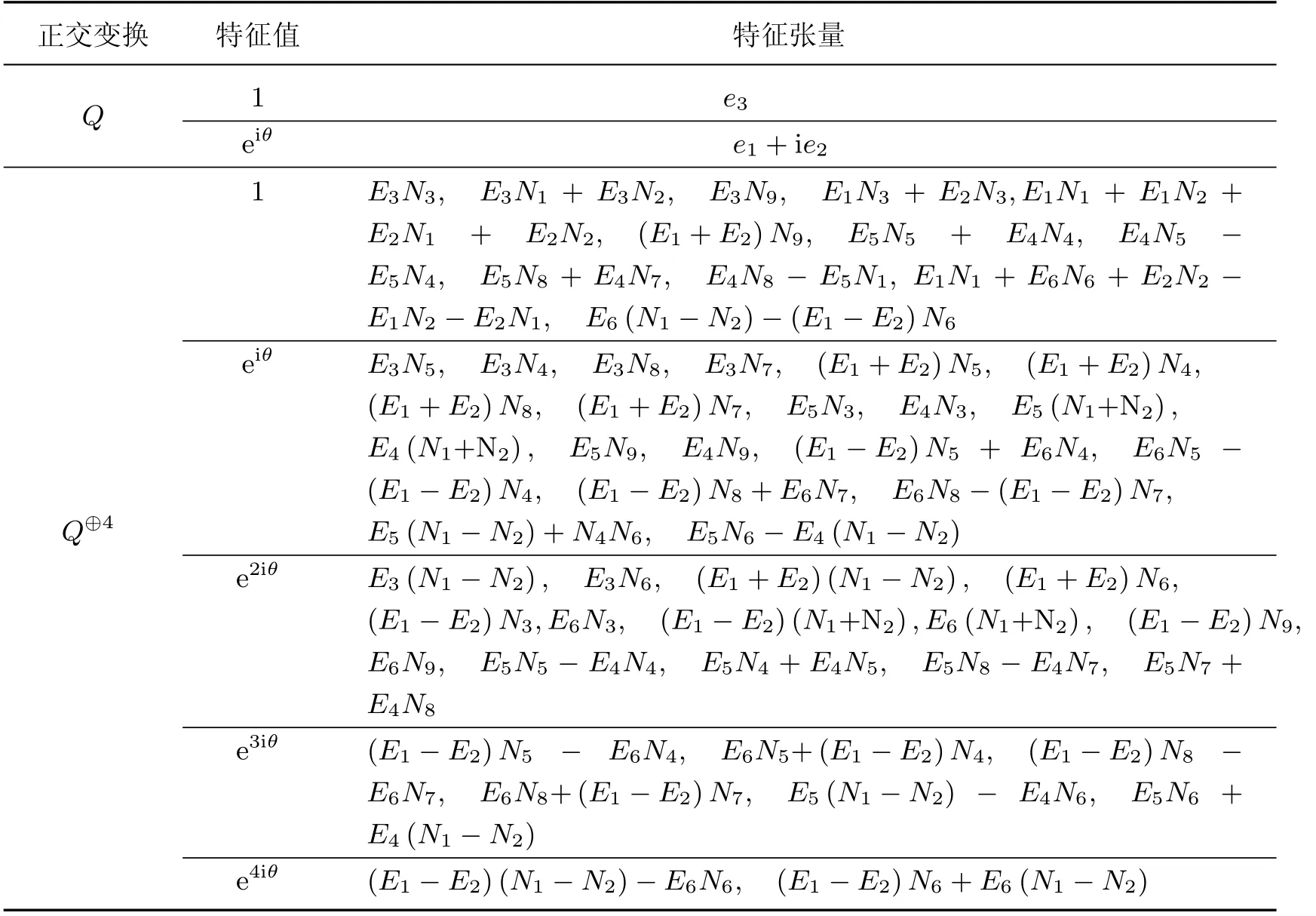
表1 正交变换Q 和Q⊕4 的特征值和相对应的特征张量Table 1 Eigenvalues and corresponding characteristic tensors of Orthogonal transformation Q and Q⊕4

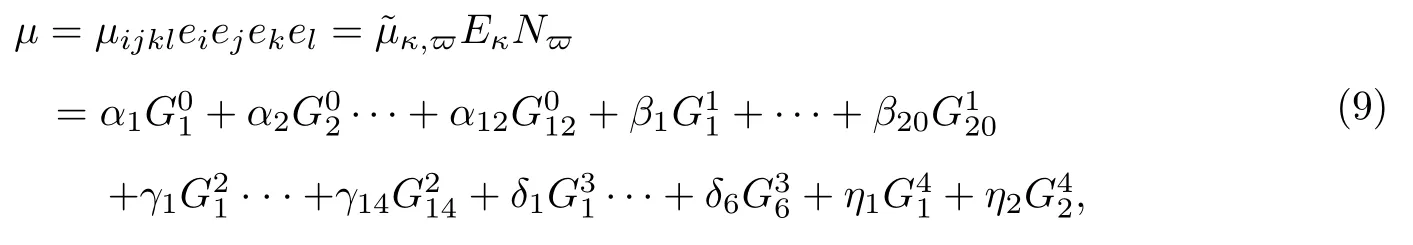
式中:κ= 1,2,··· ,6;ϖ= 1,2,··· ,9.通过Kronecker 张量积, 我们建立分量µijkl、˜µκ,ϖ和α1∼η2之间的关系.

2 各种对称条件下挠曲电系数张量的表示

利用式(9), 可以得到各晶体点群下挠曲电系数张量的具体矩阵形式.

(1) 三斜晶系.点群(1,¯1), 对称群生成元为I或−I, 则独立的挠曲电系数有54 个, 其矩阵结构为

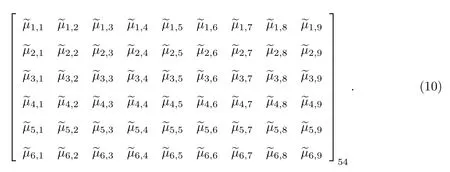
(2) 单斜晶系.点群(2,m,2/m), 群生成元Q(πe3), 即只有特征根为1、e2iθ、e4iθ所对应的特征矢量存在.因此,β1∼β20=0,δ1∼δ6=0, 独立的挠曲电系数有28 个, 其相应的挠曲电系数矩阵结构变为

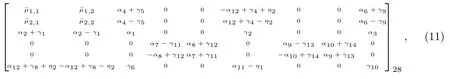
(3) 正交晶系.点群(222,mm2,mmm), 群生成元为Q(πe3),Q(πe1).此时, 独立的系数为15 个, 具体矩阵结构形式变为

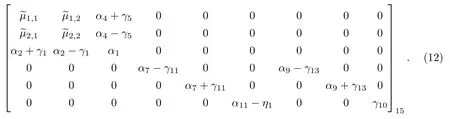
(4) 四方晶系.点群(4,,4m), 群生成元只有特征根1 和e4iθ所对应的特征矢量存在.独立系数为14 个, 具体矩阵结构形式变为

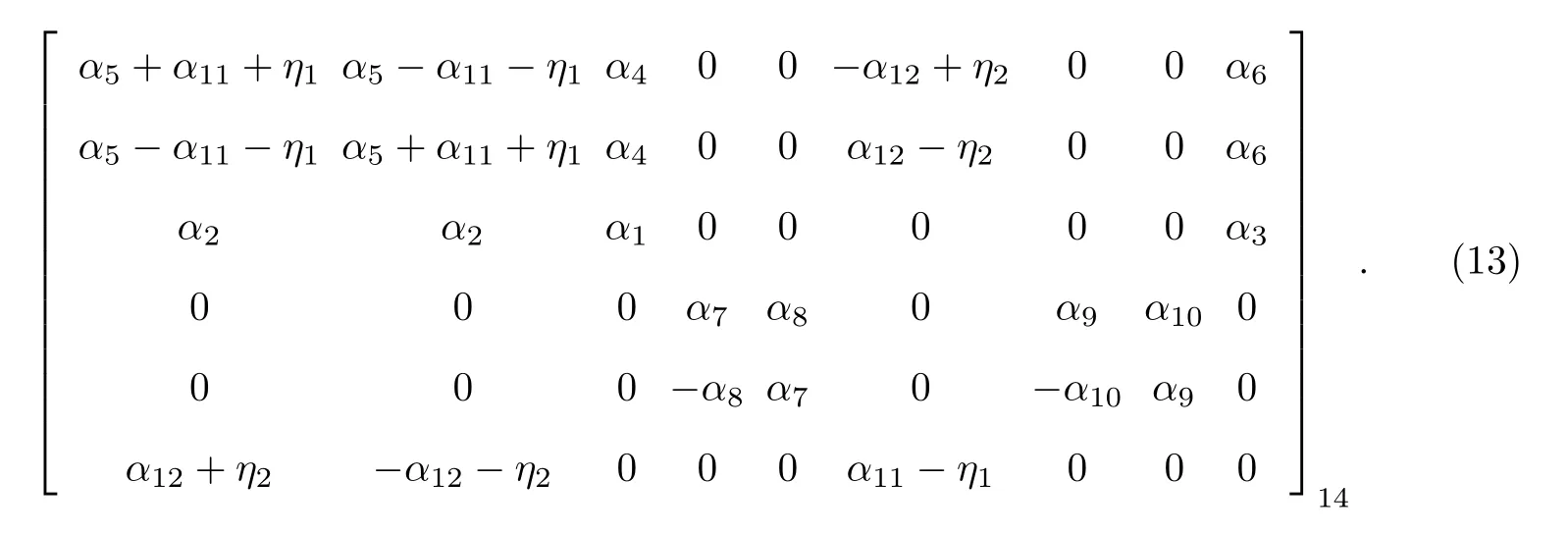
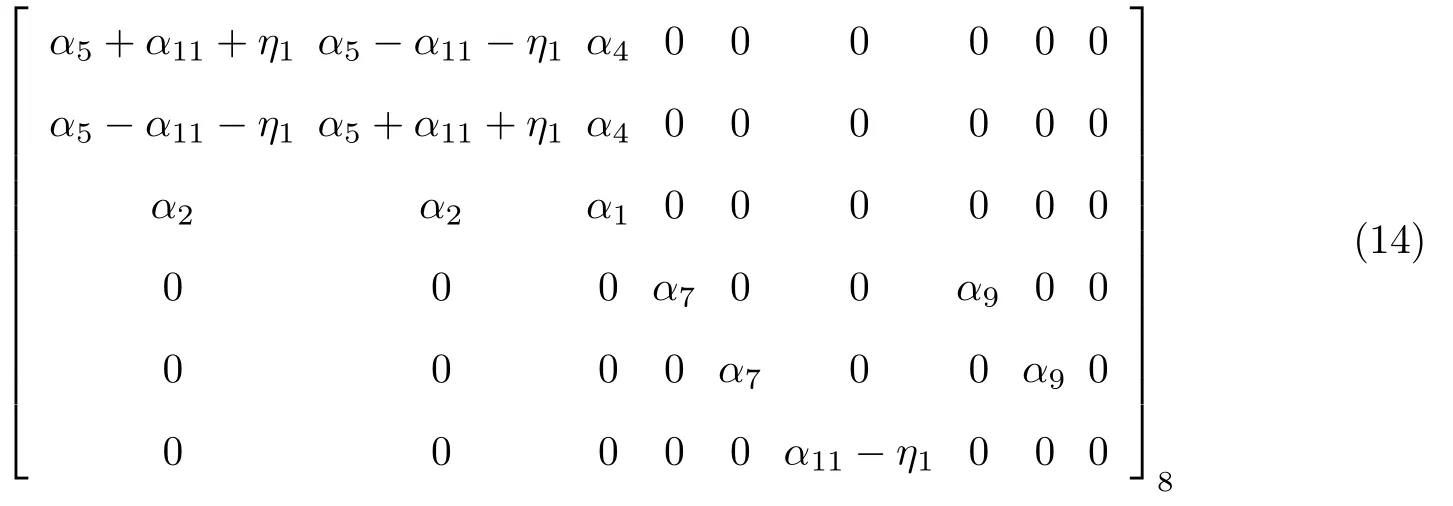
(5) 三方晶系.点群(3,), 群生成元为只有特征根1 和e3iθ所对应的特征矢量存在.独立的系数为18 个, 具体矩阵结构形式为

点群(32,3m,m), 群生成元此时独立的系数为10 个, 具体矩阵结构形式为

(6) 六方晶系.点群(6,¯6,6/m), 群生成元为只有特征根1 所对应的特征矢量存在.此时独立的系数为12 个, 具体矩阵结构形式为

点群(622,6mm,62m,6/mmm), 群生成元为此时独立的系数为7 个,矩阵结构形式为

(7) 立方晶系.点群(T,Th), 群生成元为是立方晶体的对角线单位方向.此时有5 个独立的系数, 其具体的矩阵结构形式为

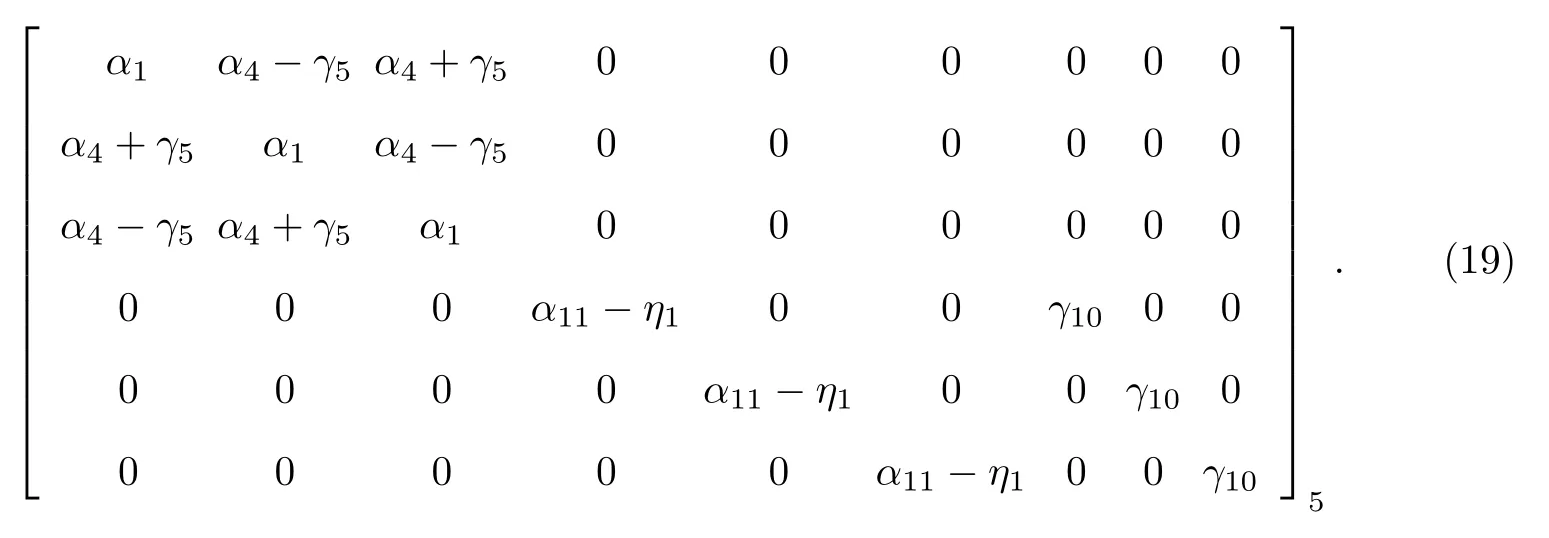
点群(O,Td,Oh), 群生成元为此时独立的系数为3 个, 具体的矩阵结构形式为

(8) 各向同性.点群, 群生成元为Q(θe3),Q(θe1).此时, 独立的系数为2 个, 具体的矩阵结构形式为

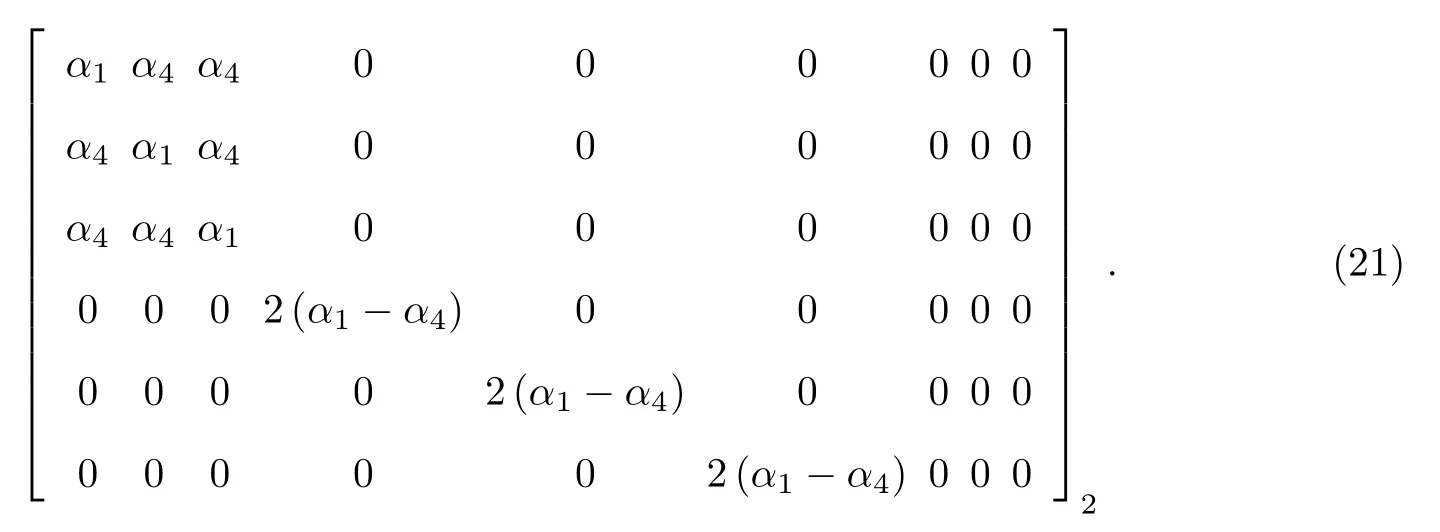
值得强调的是, 上述分析得到的挠曲电系数矩阵都是挠曲电系数张量µ=µijkleiejekel=为基的分量由分量可以通过简单的代数运算得到常用的以eiejekel为基的分量µijkl.

3 讨 论

与文献[13]中的结果进行对比, 可以发现: 对于大部分晶体点群, 挠曲电系数对称性结果一致.然而, 对于部分晶体点群如(4,¯4,4m), 挠曲电系数矩阵结果并不相同.下面分析二者的差异并论证本结果的正确性.

点群(4,,4m)的挠曲电系数矩阵[13]为

本工作中推导的点群(4,,4m)的挠曲电系数矩阵为

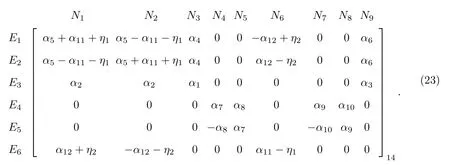
通过对比发现, 文献[13]中基e1e2e3e3的系数是−µ32, 本工作中为E6N3, 对应的矩阵值0.点群(4,,4m) 的群生成元为在这3 个群生成元下e1e2e3e3变换为−e2e1e3e3,−e1e3e2e2或−e3e2e1e1, 都可以判断出µ1233须等于0, 即本工作推导出的结果是更合理的.

4 结束语

本工作基于张量层积理论建立了满足挠曲电系数对称性的正交张量多重点积表示, 并得到了挠曲电系数张量在32 个晶体点群及各向同性下的挠曲电系数具体矩阵结构.通过与文献[13]进行对比, 验证了这些系数的正确性.这些系数可为相关挠曲电研究提供基础.