湍流热对流系统中粗糙壁面对流动结构的影响

阳建林 张义招 周 全

(1.上海大学力学与工程科学学院, 上海 200444;2.上海大学上海市应用数学和力学研究所, 上海 200072)

湍流作为一种流体流动现象存在于自然界中, 我们生产生活中见到的流体流动绝大部分都处于湍流状态.Rayleigh-B´enard(RB)湍流热对流是抽象出来的研究对流问题的经典流体力学模型, 研究RB 湍流热对流可以理解湍流运动的物理本质.RB湍流热对流的研究最早可以追溯到20 世纪初, 1900 年B´enard[1]进行了实验研究, 1916 年Rayleigh 等[2]在理论上对浮力驱动的分层流动进行了描述.RB系统由一个封闭的对流槽构成, 对流槽顶部和底部放置有可以传导热量的导板, 对流槽内部充满流体介质.对底部导板加热并对顶部导板进行冷却, 底部流体介质受热膨胀, 顶部流体介质遇冷收缩, 就会产生密度差.在浮力和重力的作用下, 底部热流体上升, 顶部冷流体下降, 开始流动.根据上下导板的温度差∆T不同, 对流槽内流体会出现不同流动状态.随着∆T增大, 对流槽内流体会由静止发展为规则的对流状态;当∆T继续增大到一定程度时, 对流槽内流体的运动转变为湍流状态.在充分发展的湍流热对流系统中, 冷热羽流分别从上下导板中生成、分离, 并在运动过程中通过自组织运动形成大尺度环流[3].

1 RB 湍流热对流

1.1 控制方程、控制参数和响应参数

RB 湍流热对流是一个复杂的强非线性系统, 流体的温度与速度耦合, 温度变化会引起密度的变化.在流体温度梯度变化不大的情况下, 通过引入Oberbeck-Boussinesq 近似[4-5]简化模型, RB 系统的控制方程组使用特征长度H、特征速度κ/H、特征温度T、特征时间H2/κ无量纲后表示如下:

式中:u是速度矢量,θ是温度,p是压力,z为竖直方向的单位矢量.式(1)∼(3)为含有热浮力项的Navier-Stokes(NS)方程连续性方程和热运输方程.由上述无量纲化的方程组可以得出RB 系统的两个重要的控制参数Rayleigh 数(Ra)和Prandtl 数(Pr), 分别为

式中:α为膨胀系数;g为重力加速度;ν为流体黏性系数;κ为热扩散系数.Ra数表示驱动流体流动的热浮力与抑制流体运动的流体耗散力的比值, 与对流槽的上下板的温差∆T和对流槽高度H的三次方成正比.Pr数代表流体本身的物理性质, 是动量扩散率与热扩散率之比,也反映黏性边界层厚度δu和温度边界层厚度δth之间的关系.流槽的几何形状采用宽高比Γ描述,

式中:D为对流槽的水平方向长度;H为竖直方向长度.

RB 对流系统还有两个重要的响应参数, 分别为Nusselt 数(Nu)和Reynolds 数(Re),

式中:Nu用于描述系统的传热效率;λ是流体的热传导系数;Q为通过对流槽的热通量;Re表示流体所受的惯性力和黏性力之比, 是系统的无量纲速度;U可以是大尺度环流的特征速度,也可以是流场中速度均方根的值.

1.2 研究现状

粗糙边界作为一个增强传热的方法广泛应用于湍流热对流中, Shen 等[6]的实验以水为对流介质, 在对流槽上下导板表面均匀地排布了金字塔状的粗糙元, 发现当Ra数超过某一临界值时, 系统的整体热输运效率可以增强约20%.Du 等[7-8]的工作更进一步地表明, 大尺度环流引发的强水平剪切流动与粗糙元相互作用会在粗糙元之间形成二次涡, 有利于羽流的形成, 从而可以极大地提高系统的整体热输运效率, 实验测得Nu数增量超过76%.Shishkina 等[9]对底部粗糙元剖面为长方形的方形对流槽进行数值模拟, 并基于二维Prandtl-Blasius 边界层方程提出了一种计算粗糙元引起的Nu数偏差的分析模型.Liot 等[10]对顶板保持光滑, 下底板布置有方形粗糙元的方形对象槽进行实验, 值得一提的是此工作中的实验装置非常大, 高度和宽度达到2.5 m, 厚度为0.5 m, 能够测得非常精细的速度场, 研究发现粗糙元之间流体存在外部对流和流体交换时能显著增强传热.Xie 等[11]对底部粗糙元为金字塔型的圆柱形对流槽进行实验, 通过定义粗糙元高宽比λ, 7.5×107≤Ra≤1.31×109,Pr数从3.57 增加至23.34, 发现随着λ从0.5 增加至4,Nu和Ra的标度律关系大致可以分为3 个区域(区域一标度律和光滑相比并无明显变化, 区域二标度律从0.36 上升至0.59 是由热边界层主导的, 区域三从0.30 上升至0.50 是由黏性边界层主导的), 并给出Re和Ra的标度律关系从0.471 增加至0.551 是由大尺度环流的动力学发生变化引起的解释.Stringano 等[12]研究了粗糙元尺寸h对系统传热的影响, 结果表明当系统的平均温度边界层厚度小于粗糙元尺寸时可以观测到传热增强.上述研究结果都表明粗糙元能够增强系统的传热.

粗糙元被认为可能有助于观测到“终极区间”, 因为粗糙元的存在会破坏边界层结构.Toppaladoddi 等[13]使用直接数值模拟计算带有正弦形状粗糙元的RB 系统, 通过改变粗糙元波长, 发现存在一个最优波长使得Nu数与Ra数接近满足1/2 的标度律.根据“终极区间”理论, 只有在Ra数很大时才能观察到1/2 标度律.而Zhu 等[14]采用相同的粗糙元将Ra数扩展到1012, 发现在Ra数相对较低的区间内能够观察到1/2标度律, 但是随着Ra数增加,标度律指数会重新回到1/3,Nu数与Ra数1/2 标度律只能存在小范围Ra数内, 以此证明Toppaladoddi 等[13]观测到的并不是“终极区间”.最近, Zhu 等[15]采用多尺度粗糙元, 成功实现了在广范围Ra数内保持1/2 的标度律, Xia[16]则认为这是一种通过调整RB 系统边界形状来控制传热的新方法.

Zhang 等[17]通过改变三角形粗糙元高度h, 模拟二维方形对流槽, 结果表明: 对流槽加入粗糙元后并不是总意味着传热增加, 在粗糙元高度较小时反而会使传热减小;当粗糙元的高度h较小时, 相邻粗糙元间腔体内部的流动主要受流体的黏性所控制, 这时热流体被限制在这些腔体内部无法充分混合, 导致腔体内部温度边界层厚度增加, 从而阻碍了系统的整体热输运效率;相反, 当h足够大时腔体内部逐渐增强的流体流动可以有效地混合冷热流体, 导致更多更强的羽流结构生成, 使Nu数急剧增加.

上述工作主要侧重于研究粗糙壁面对传热的影响, 而对Re数的关注度有所欠缺, 因此本工作主要在前人工作基础上使用数值模拟的方法研究粗糙元高度对Re数的影响.

2 计算模型及参数

图1 为RB 对流系统计算模型.对流槽宽度为D、高为H, 底板加热温度为无量纲温度0.5, 顶板冷却温度为无量纲温度−0.5;对流槽的侧壁保持绝热, 所有边界均为无滑移边界条件.对流槽上下板分布有等腰直角三角形形状的粗糙元, 粗糙元的顶角保持直角不变, 通过改变粗糙元的数量来改变粗糙元的高度h, 且保持粗糙元与对流介质的接触面积不变, 即达到改变边界粗糙程度又不影响加热接触面积的效果.易知加入粗糙元后加热面积是没有粗糙元(光滑)情况下的1.41 倍.

图1 RB 对流系统计算模型示意图Fig.1 Schematic diagram of calculation model on RB

本工作采用交错网格四阶差分格式求解控制方程, 采用浸入边界法处理粗糙元的边界问题, 采用非等距网格跟踪粗糙面附近的细节, 并在求解过程中确保热边界层内有16 个以上的网格点, 以满足网格分辨率[18].本工作计算所使用代码在Zhang 等[17]、Bao 等[18]和Chen等[20]的工作中已得到了验证, 计算过程主要在“天河二号”超算中心进行, 所有算例保持宽高比Γ=1 不变(D=1,H=1).Ra数的计算区间为107≤Ra≤109,Pr=0.7, 粗糙元数量由2个增加到70 个, 对应粗糙元高度h由0.125 减小至0.014.

3 结果分析和讨论

Re数和系统内流体的运动相关, 可以表征系统的无量纲流动速度.本工作中Re数使用速度均方根Urms进行计算, 结合式(6), 有

式中:表示时间和空间上取平均.

图2(a)为Ra=108,Pr=0.7 时Re数随粗糙元高度h的变化规律, 可以发现: 随着粗糙元高度h的增加,Re数首先有一个减小的过程, 达到极小值后Re数开始增加, 拐点位于粗糙元高度h=0.05 处, 对应的粗糙元数目为10;当Re数增加到极大值后, 随着高度h继续增加,Re数又有一个减小的过程, 此时拐点位于粗糙元高度h=0.1 处, 对应粗糙元数目为5.

光滑情况(粗糙元高度h= 0) 下的Re数记为Re(0), 对粗糙情况下Re数进行标准化, 结果如图2(b)所示, 其中虚线表示Re(h)/Re(0)= 1, 即光滑情况Re数与粗糙情况Re数相等.可以发现: 粗糙元对Re数的影响很大, 随着粗糙元高度不同, 对Re数既有增强作用也有抑制作用.只有当粗糙元高度h足够大时, 粗糙元才能对Re数有增强作用, 但是当粗糙元高度h极大时,Re数又会受抑制.

粗糙元对Re数的作用非常复杂, 根据Re数随粗糙元高度h变化的2 个拐点可以大致分为3 个区间(见图2(b)).那么Re数随粗糙元高度h如此变化的物理本质是什么呢？Re数由速度均方根Urms、对流槽高H和流体黏性系数ν共同决定, 算例中固定对流槽宽高比Γ和Pr数不变, 只改变粗糙元高度h, 那么一定是h影响Urms, 从而影响Re数.

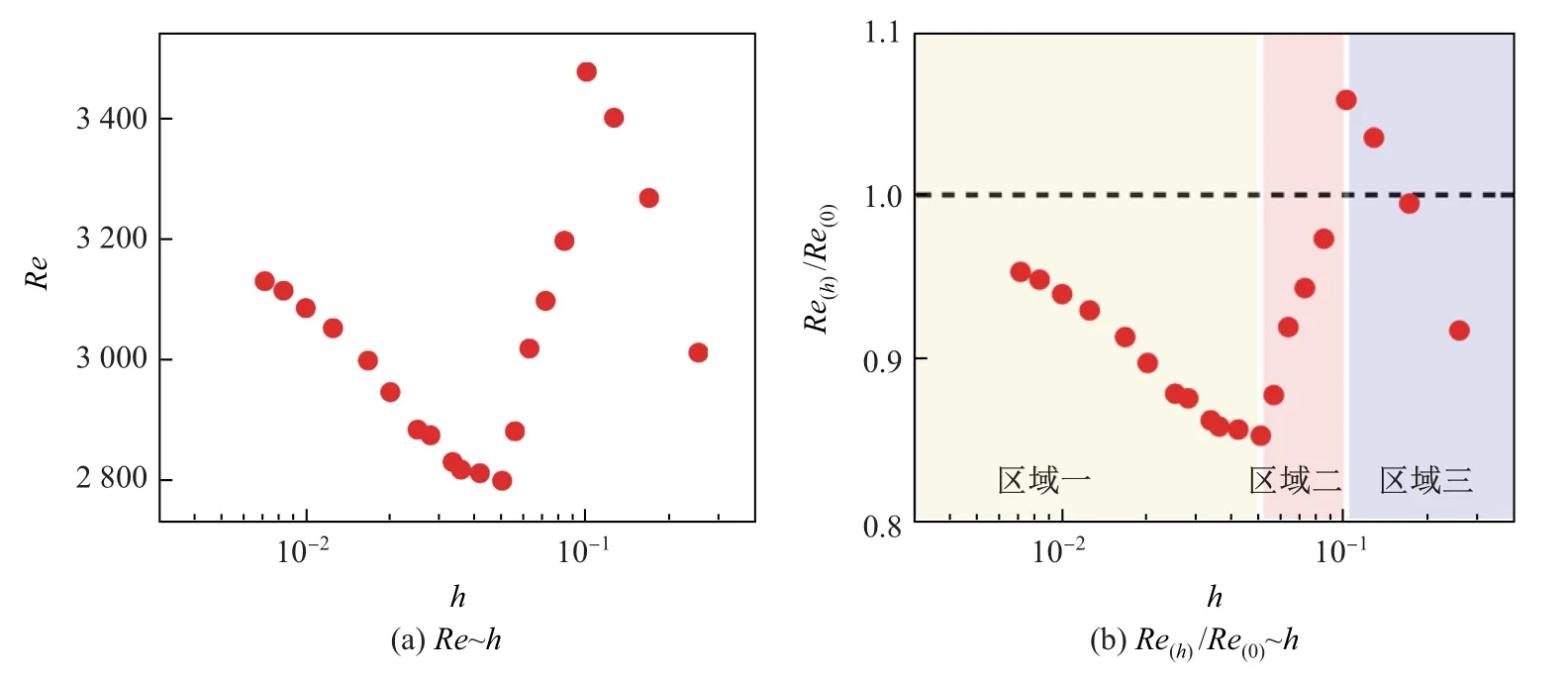
图2 Re 数随粗糙元高度h 的分布(Ra=108, Pr =0.7)Fig.2 Re as a function of the roughness height h (Ra=108, Pr =0.7)

图3 是速度时间平均场的分布, 其中箭头代表速度的方向.区域一(见图2(b))内Re数减小对应图3(a)变化到图3(b), 从图中可以发现都存在一个明显的大尺度环流, 但是在大尺度环流作用下, 图3(a)中速度均方根Urms最大值为0.502, 而(b)中最大值为0.423.从Urms分布上来看, 图3(a)中Urms值大的点(红色区域)明显多于图3(b), 主要沿大尺度环流外侧分布, 分别呈椭圆状和呈圆形状.随着粗糙元高度h增加, 大尺度环流发现空间受限, 大尺度环流形状逐渐由椭圆转变为圆形,Urms随着减小导致Re数随h的减小, 这也印证了Re数与大尺度环流的动力学密切相关[12].此外二次涡的作用也不可忽略, 二次涡是在大尺度环流剪切作用下粗糙元之间流体形成类似于“顶盖流”[21]的流动.如图4(a)所示, 粗糙元高度h较小时二次涡发展受限, 混合作用弱, 流动速度小[17], 这导致大量流体“滞留”在粗糙元之间, 对Re数贡献非常小.

区域二(见图2(b))内Re数增加对应图3(b)变化到图3(c), 在此区域内Re数随着粗糙元高度h增加而增加, 此时图2(c)中粗糙元高度h比图3(b)中更大.随着h的增加, 粗糙元对大尺度环流的抑制作用应该更强, 为何会如此反常呢.我们认为主要有两个方面原因: 首先是羽流的作用, 羽流之间互相作用形成更大尺度的涡流进而最终形成大尺度环流[3];其次是二次涡的作用.Du 等[7-8]的研究结果表明粗糙元有利于羽流的生成, 随着粗糙元的高度增加, 粗糙元对羽流生成作用越有利, 随着羽流大量生成, 又为大尺度环流注入了动力, 这就导致了Urms增加从而Re数增加.图4 所示的是粗糙元附近的Urms, 其中图4(a)对应图3(b)下底板正中间局部放大部分, 图4(b) 对应图3(c)下底板正中间局部放大部分.与区域一不同, 随着粗糙元高度h增加, 粗糙元之间腔体越大, 更有利于二次涡发展, 二次涡越强[21].对比图4(a)和(b)明显可以发现, 由于二次涡变强图, 4(b)中的Urms无论从数值大小还是分布都大于图4(a).

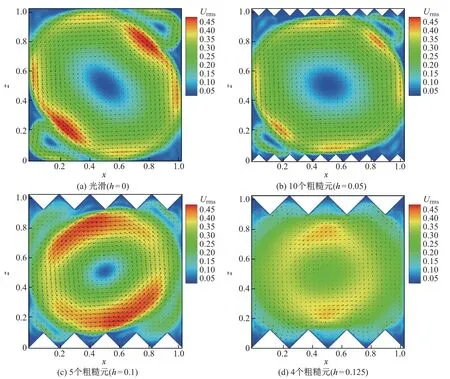
图3 速度时间平均场对应不同粗糙元高度h 的分布(Ra=108, Pr =0.7)Fig.3 Time aver velocity fields for differnet roughness height h (Ra=108, Pr =0.7)

图4 粗糙元附近速度时间平均场(Ra=108, Pr =0.7)Fig.4 Time aver velocity fields near rough element (Ra=108, Pr =0.7)

由图2(b)中的区域三可知,Re数随着粗糙元高度h增加而减小.对比图3(c)和(d)可以发现, 随着粗糙元的进一步增加, 大尺度环流的发展空间变得很小, 这导致大尺度环流变弱, 此时Urms最大值仅为0.399.并且大尺度环流的影响范围也变得十分有限, 这导致Urms在空间分布上不如图3(c).

总体来说,Re数随粗糙元高度h的分布主要是粗糙元对大尺度环流抑制作用以及与粗糙元对羽流的生成和二次涡的促进作用竞争的结果.当粗糙元对羽流的生成和二次涡的促进作用大于粗糙元存在对大尺度环流的抑制作用时,Re数增加, 反之则减小.

图5(a)给出了不同Ra数时Re数随着粗糙元高度h的变化规律.可以发现: 对于所有Ra数依旧能够符合随着粗糙元高度h增加Re数有一个先减小后增加再减小的变化规律;但是在不同Ra数下,Re数分布的拐点有所不同,Ra=107时拐点对应粗糙元高度最大,Ra=109时拐点对应粗糙元高度最小.这是因为随着Ra数增加, 大尺度环流剪切能力越强, 越易于增加二次涡的强度, 也有利于羽流的产生, 所以当Ra数很大时, 粗糙元高度h很小就能对Re数增加起到促进作用.

图5 不同Ra 数下Re 数随粗糙元高度h 的分布(Pr =0.7)Fig.5 Re as a function of the roughness height h for different Ra (Pr =0.7)

对于光滑情况,Ra数与Re数大致满足Re∼Ra0.6的标度律关系.Zhang 等[22]的研究结果表明, 当Pr=0.7 时Re∼Ra0.59, 本工作中Re∼Ra0.57, 二者结果相近.粗糙元对标度律的影响如图5(b)所示, 其中虚线为光滑时Ra数与Re数的标度律0.57.在粗糙元高度h= 0.05 时,粗糙元能提高Ra数与Re数的标度指数至0.62.固定h= 0.05,Ra= 109时粗糙元已经能促进Re数增加, 而Ra= 108是抑制Re增加,Ra= 107则抑制更多.这意味着粗糙元高度h= 0.05 时,Ra= 107的Re数是小于光滑情况的, 而Ra= 109的Re数是大于光滑情况的,直接导致了标度律指数相比于光滑情况有所增加.同理, 如果粗糙元对Ra= 109时Re数的抑制作用比Ra= 107时更大, 则表现为标度律指数减小, 如图5(b)前半段.标度律指数变化的深层原因还是因为随着Ra数增加, 二次涡在很小的粗糙元高度h就能对Re数起促进作用.

4 结 论

本工作通过数值模拟的方法研究二维粗糙边界RB热对流系统中粗糙元高度h对Re数的影响.

(1) 同一Ra数下, 随着h的增加,Re数有一个先减小后增加再减小的过程, 这是粗糙元对大尺度环流的抑制作用与粗糙元对羽流的生成和二次涡的促进作用相互竞争所导致的.当粗糙元对羽流的生成和二次涡的促进作用大于粗糙元存在对大尺度环流的抑制作用时,Re数会增加.

(2) 不同Ra数下, 粗糙元对羽流的生成和二次涡的促进作用所需粗糙元高度h不同, 导致了粗糙情况下Ra数与Re数的标度律关系异常.