非线性Lamb波脉冲激励的零频分量理论

孙晓强 张晋源 胡宁

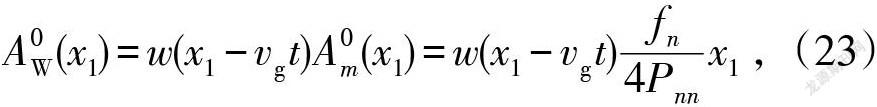
摘要 为方便利用非线性Lamb波脉冲激励零频分量进行板材结构早期损伤超声无损健康监测，基于二次材料弱非线性，在基波和零频分量群速度相等的情况下，推导非线性Lamb波脉冲激励零频分量的理论解。以汉宁窗调制的短脉冲激励为例，建立仿真模型，提取仿真零频信号，制作零频信号传播动画，展示对称模态零频分量克服相速匹配条件的限制进而可持续累积的特征。理论仿真结果与分析讨论表明，零频模态为对称模态，零频形貌与窗函数形貌相似，基波群速度失配和色散可以分散零频分量能量进而影响零频形貌，零频分量可持续累积特性不受其影响，与二次谐波和混合波检测技术相比，非线性Lamb波零频分量检测技术具有一定的优势。

关 键 词 结构健康监测;非线性Lamb波;零频分量;材料弱非线性;材料早期损伤

中图分类号 TG115.285;TB553     文献标志码 A

文章编号：1007-2373（2021）06-0001-12

Abstract For the convenience of using nonlinear Lamb wave pulse excitation zero frequency component to monitor plate-like material early stage damage， based on the quadratic weak material nonlinearity， the theoretical solution of zero frequency component induced by nonlinear Lamb wave pulse is derived under the condition that the group velocities of fundamental wave and zero-frequency component are equal. A simulation model is established. A Hanning windowed tone burst signal is adopted as the excitation signal. The propagation animation of zero frequency component is obtained. The limitation of phase-velocity matching is overcome and the energy carried by zero frequency component can accumulated continuously. Theoretical results simulation results and discussion analysis show that the shape of the symmetric mode zero frequency component is similar to the shape of the window function. The shape of zero frequency component is influenced by zero frequency component energy dispersion which induced by the group velocity mismatch and dispersion of the fundamental wave. The sustainable accumulation characteristics of the zero frequency component are not affected. Compared with the second harmonic and mixing wave detection technology， nonlinear Lamb wave zero-frequency component inspection technique has certain advantages.

Key words structural health monitoring; nonlinear Lamb wave; zero frequency component; weak material nonlinearity; material early stage damage

0 引言

板壳结构性能优异，被各行各业广泛采用。这些板壳类结构材料在使用过程中，或多或少会受到应力、高温、高压和腐蚀等的作用，非常容易产生疲劳、塑性、腐蚀和蠕变等损伤，使得板材性能逐渐退化，容易引起爆炸、断裂和危险物质泄露等安全事故，造成重大社会和经济损失。因此，研究强有力的无损监测技术，对这些板壳结构定期进行可靠性检测评价和维护，是我国国民经济生产及生活中一个非常重大的研究课题。

经过多年的研究和发展，目前已经存在多种，相对较为成熟的无损检测和评价技术。如液体渗透、磁粉、涡流、X射线和线性超声波等技术。然而，这些传统技术，只能检测材料中的宏观缺陷损伤（一般为毫米级），比如宏观裂纹、夹杂、脱层和气孔等;而针对微纳尺度早期损伤，如材料位错和滑移等早期损伤，并不敏感[1]。已有的研究表明，一般情况下，在材料产生宏观损伤之前，材料早期损伤占据了材料使用寿命的绝大部分。尤其是，当材料[2]发生疲劳损伤时，材料整个疲劳寿命的80%～90%[1-3]都是由材料早期损伤性能退化占据。故研究发展和优化针对材料早期损伤的无损检测方法，对保障生产生活安全，意义重大。

近年来大量研究发现[1-15]，非线性超声波检测技术对材料微观结构的改变，如位错密度和微裂纹密度等的变化，十分敏感，能够有效地检测和评价材料的早期损伤及其损伤的程度。尤其是针对板材发展起来的非线性Lamb波导波检测技術，因其传播距离远，检测范围广，对早期损伤敏感等优点，吸引了众多研究者的关注和研究。

在传统非线性Lamb波早期损伤检测领域，针对二次谐波检测技术，人们发表了大量的理论仿真和实验研究成果[1-14]。目前，针对二次谐波的研究，少有较新颖的成果见刊，二次谐波的研究在传统的框架下已经逐渐趋向成熟。而二次谐波检测技术的实际应用，却存在着较多的技术难题。Lamb波本身具有复杂的色散和多模态特性;二次谐波可累积需要满足两个条件：非零能量流从基波流入二次谐波，基波和二次谐波相速度相等，实际应用时如果为了方便信号处理，还需要基波和二次谐波群速度相等;通常情况下，二次谐波的能量是微弱的，容易受到噪声的干扰;来自于传感器、电路、耦合剂等的非线性信号与待测材料的非线性信号叠加在一起，难以判断测得的非线性是来自待测材料还是测试系统。

相速匹配条件不满足时，随着基波传播距离增加，二次谐波将周期性振荡而不能线性累积，这限制了二次谐波的应用。一般地，材料二次非线性是一种较弱的非线性，在相速失配限制二次谐波可持续线性累积后，二次谐波信号通常比较弱且容易被噪声淹没[16]。为了克服相速失配，研究者们大致提出了两种解决办法。第一种是通过寻找频率模态对，筛选出的基波和二次谐波的相速度刚好相同，从而达到二次谐波强度随着基波传播而线性增长的目的。人们利用S1-S2模态对（S1是一阶对称模态基波，S2是二阶对称模态二次谐波）来测量材料非线性[17-18]，如拉伸塑性损伤和疲劳损伤[19-20]、温度疲劳损伤[21]、蠕变损伤[22-24]。另外，对其他的模态对，如A2-S4[25]，S2-S4[26]等，也有所研究。然而，这种方法也存在不少需要克服的问题[27]。比如，这些频率模态对是分散的，而且数量有限，不能实现宽频带范围内的相速度匹配;实际应用中，激发信号的中心频率很难严格符合预期选定的频率，并且接收到的信号通常是复杂难处理的[27]。第二种是利用低频S0模态波的低色散性，使相速匹配条件近似满足，使得二次谐波能量在基波传播较大距离范围内近似线性累积。低频S0模态波在较宽频率范围内近似满足相速匹配条件，突破了单个频率对的限制，鲁棒性好;单个低频S0模态信号更容易激发，色散相对较弱，信号处理也较简单。近年来，低频S0模态得到了研究者的广泛关注，文献[28-29]利用Lamb波S0模态波检测微裂纹，文献[27]指出低频S0模态波可以弥补模态频率对的不足，为低频S0模态波做了系统性的模拟研究。文献[30]通过实验和模拟研究确认了低频S0模态检测材料非线性的有效性。

为了确认非线性的来源，实现损伤定位，近年来混频检测技术得到了广泛研究[31-44]。自1963年Jones[45]给出了针对体波混频技术的共振条件之后，混频技术研究越来越活跃。混合波技术的核心对象是非线性波解中的和频与差频，混合波和二次谐波理论上同出一辙，使用混合波技术时，往往是让两束波束在某个位置相遇，如果材料存在非线性，两束波相遇互相作用后将激发出对应的和频与差频成分波，新产生的特定的和频以及差频成分，被称为混合波。由于混合波只会在两束基波混合区域产生，如果混合区域存在材料早期类型的损伤，比如位错、微裂纹等，那么这个混合波就对应于该处的损伤特征，于是混合波便可用于检测材料早期损伤。耦合剂、电路、传感器探头等检测系统自身的非线性，一般情况下，对混合波没有贡献，因为基波并没有在电路和传感器等处相遇混合，这样混合波检测技术就克服了二次谐波检测技术难以辨识非线性来源的困难。对于平行发射的共线基波，一种情况是，两个先后同向平行发射的基波，先发射的基波速度慢一些，后发射的速度快一些，当两者相遇时，如果相遇区域存在损伤，将会激发损伤混合波信号;另外一种情况是，两个基波在材料两端对向发射，然后在某个区域混合，这样产生的混合波称为对向混合波。对于非平行发射的非共线基波，基波在损伤区域相遇混合相互作用，也可激发混频信号。

然而，混频信号的产生也需要满足一定的条件[46-48]，需要输入的基波满足一定的频率比以及满足一定的输入角度;并且混合波技术还存在一些技术难题，由于混合波混合的区域大小有限，实际应用时，事先并不知道损伤发生的局部位置，对于大面积检测，需要不断移动混合区域进行扫描检测，这对信号的发射和处理提出了一定的挑战。

实际上，波在非线性介质中传播，除了激发倍频、和频与差频，还会激发零频。零频分量，又被称为静态位移或者直流分量，在体波中很早就受到了研究者们的关注。20世纪早期出现了一些和静态位移导致的应力相关的讨论，1925年，Brillouin[49]认为零频导致的应力与波动质点动量时间平均值的变化有关，其他一些研究者[50]认为零频导致的应力直接相关于材料的非线性特性。20世纪80年代早期，Narasimha[51]使用传感器来接收零频信号，并用零频项来测量材料的非线性系数，指出零频形貌为直角三角形样形状。2006年，Jacob[52]使用激光来探测零频，通过滤波手段展示了有限宽脉冲基波激发的零频的大致形貌，其形貌与基波脉冲的波包类似，并非直角三角形样形状，并指出零频分量随着基波能量增加而线性增加。2007年，Narasimha等[51]使用传感器探测零频应变分量，并提出了一种新的信号处理提取零频分量的方法。随后Narasimha等、Qu等和Jacob等针对零频分量做了一些出色的研究[53-55]，奠定了使用零频测量材料非线性的基础。

然而，这些报道的研究对象均为体波中的零频，之后多年均无零频相关研究报告。2017年Sun等[56]在厦门举办的无损检测大会上首次报道了Lamb波中零频分量的相关理论研究结果，并指出Lamb波激發的零频累积条件只有一个，即非零能量流从基波流入零频，而二次谐波累积所需要的相速度匹配条件不再是零频可累积的必要条件，零频可持续累积;指出Lamb波基波激发的零频项积分值，比同一个Lamb基波激发的二次谐波积分值更大;指出零频模态为对称模态。2018年Wan等[57]通过COMSOL仿真研究了Lamb波激发的零频，研究结论与Sun等的理论结果相符，并进一步展示了Lamb波零频的大致形貌与基波波包形状类似;指出Lamb波零频传播群速度和相速度均相同且与S0色散曲线上的频率为零处对应的速度值相等。随后，Sun等[13]通过理论仿真和实验再次验证了Lamb波零频分量用于板材早期损伤检测的可行性，指出与Lamb波二次谐波相比，Lamb波零频分量检测技术具备一定的优势。2020年，文献[58]通过理论和仿真研究了块体材料中均布随机裂纹产生的零频，指出体波零频检测技术可用于块体材料早期微裂纹损伤检测。针对PZT探头是否响应零频的争论，文献[15]通过PZT实验和激光实验验证了PZT可以有效探测到零频信号，并利用PZT探测零频信号，进一步利用零频检测技术检测了材料局部弯曲塑性损伤。Deng[59]用常规探头有效探测零频信号，Chen等[60]实验探测了非线性Lamb波零频分量信号，再次证实了零频信号可持续累积特性。非线性零频检测技术，尤其是针对板壳材料的非线性Lamb波零频分量检测技术，有望中和二次谐波和混合波的优势，克服其对应的缺点，应用潜力巨大。

非线性Lamb波脉冲激励的零频分量相关理论是零频检测技术的基础，搞清楚相关理论是有必要的，目前相关理论研究比较稀少。Sun等[13，56]发表了一些相关理论研究结果，然而，其理论主要考虑的是单一频率无限宽信号激励，实际更为常用的激励信号为脉冲激励，有必要开展相关研究。

1 理论

1.1 无限宽时域信号激励

仿照文献[5-6，8，10]，设[E]为Green-Lagrange 应变张量，[u（X，t）]为位移张量，则有：

式中：X表示物体质点微元的初始构型坐标;H表示位移梯度。 通常采用Landau and Lifshitz 超弹性模型[61]来描述材料的弱非线性各向同性本构关系，其对应的应变能函数为

式中保留到[H]的二次项。

考虑均匀各向同性厚度为[2h]的薄板，质点运动限制在[x1-x3]平面内，其中Lamb导波沿[x1]方向传播，[x3]方向与板面法向量[n3]方向重合。Lamb波薄板上下两个边界为自由无约束边界，其波动方程和边界条件可写为

采用摄动微扰法，设式（8）的解可以分解为

方程（10）可以拆解为两组方程，第一组方程组为一阶线性近似波动控制方程组：

这正是线性Lamb波问题的波动控制方程和边界条件，易知其解为

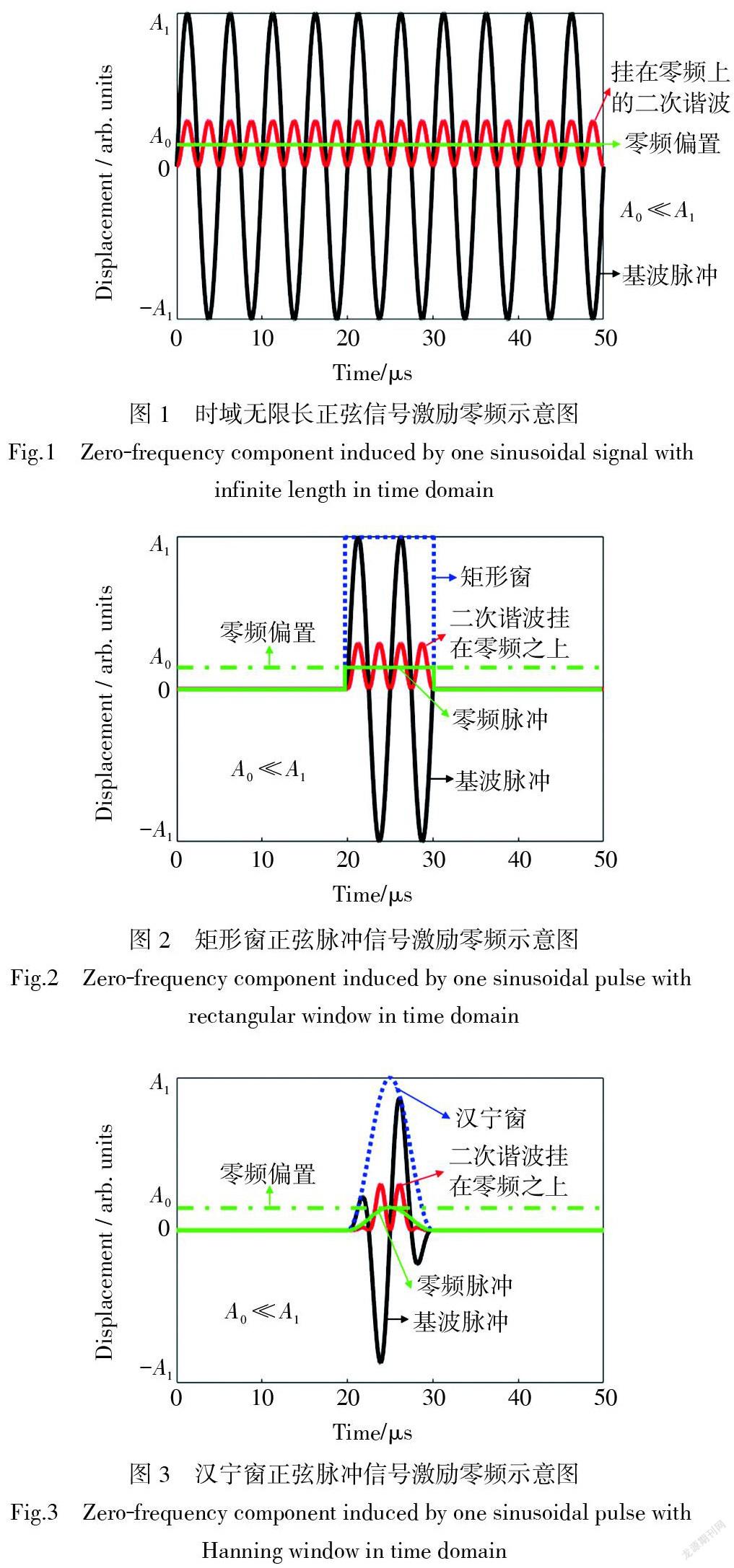
式（22）为时域无限长基波信号激励零频分量的理论表达式。非线性源的二次平方属性与三角函数倍角公式，保证了零频与二次谐波两项之前常系数的相等关系;且零频分量在产生和传播过程中相位不变，自动满足相速匹配条件或者说不需要相速匹配条件，零频总是相长叠加进而可持续累积：式（22）也可以通过取相速匹配时的二次谐波解直接得到[13]。如果记基波幅值为[A1]，零频幅值为[A0（A0≪A1）]，则基波二次谐波及零频的示意图如图1所示，图中黑色正弦波代表基波，亮绿色直线代表零频，红色正弦波代表二次谐波，其中二次谐波挂在零频上，二次谐波的平衡位置正好与零频偏置重合。

1.2 脉冲信号激励

时域无限长基波信号激励零频分量的理论解，是零频分量发生激励最基础的理论，由此可以推导出其他复杂的零频分量发生激励理论解。比如，对于实际应用中常用的检测信号，基波信号通常为脉冲信号，时域宽度是有限的，此时，各种脉冲信号激励的零频理论解，只需要在式（22）的基础上乘上相应的脉冲调制窗函数即可。显然，脉冲信号激励的零频分量解为

式中：[w（x1-vgt）]定义为伴随窗函数;[vg]为零频传播群速度。伴随窗函数包含两层含义：一层含义是初始基波脈冲对应的加窗函数;一层含义是基波脉冲在材料中传播时加窗函数受到材料的影响和调制，比如多模态和色散等对窗函数的影响和调制。

为了简单，暂不考虑Lamb波的色散和多模态，并假定基波和零频群速度相等，即认为伴随窗函数形状并不发生变化，只是随着基波传播而由近及远地平行移动，且零频脉冲最大幅值可持续累加而随着波传播距离增加线性增大。图2展示了一个中心频率为200 kHz的矩形窗调制正弦脉冲激励的零频脉冲示例，黑色实线表示基波脉冲，蓝色虚线表示矩形窗函数，亮绿色点划线表示相应频率无限长信号在该处激励的零频偏置，亮绿色实线表示零频脉冲，红色线表示非线性波，其中二次谐波挂在零频脉冲之上，易知此时零频形貌与矩形窗函数相似。若将该矩形窗改为常用的汉宁窗，如图3所示，类似地，基波经汉宁窗调制的脉冲信号，激励的零频脉冲形貌依然与汉宁窗函数形貌类似。

需要说明的是，针对高频Lamb基波脉冲，由于色散和多模态等的影响，[w（x1-vgt）]将变得多样化和复杂化，理论上零频脉冲的积分面积依然随基波传播距离线性累积，即基波群速度和色散只影响零频脉冲的形貌，不改变零频累积特性。另外，若基波群速度和零频群速度不一致，不同时间激励的零频将存在一定的分散而无法完全重叠，此时只需在式（23）基础上对分散的零频求和即可，该思路与文献[9]提取时域二次谐波脉冲信号的思路类似，相应示例可参见文献[60]，对此不再做过多的讨论。由于零频来源于平方非线性中的平方常数项，二次平方确保了零频的对称性为对称模态。

2 有限元仿真

2.1 零频形状特征

在工程应用中，最长使用的超声检测脉冲为汉宁窗函数调制的波包，现以汉宁窗函数调制脉冲为例展开仿真研究。不考虑阻尼，采用商用有限元分析软件Abaqus（Version 6.14，Dassault Systems Simulia Corp.，Providence，RI，USA）建模分析非线性Lamb波相关问题。Landau-Lifshitz弱非线性超弹性本构模型用户子程序，通过FORTRON进行二次开发，集成于软件Abaqus中，材料本构模型的具体参数如表1所示。

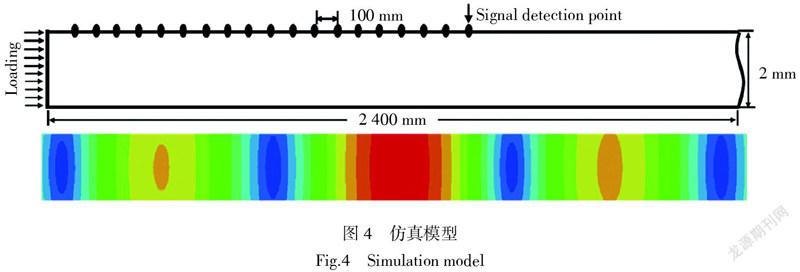
仿真模型为长2 500 mm，宽68 mm，厚2 mm的铝板，考虑到Lamb问题为平面应变问题，建立如图4所示的二维模型，模型厚度为2 mm，为了消除反射波的影响，模型长设置为2 400 mm，为了消除仿真整体模型在加载时发生刚性位移，模型右端施加位移固定约束。汉宁窗位移激励函数满足方程：[x（t）=A2sin（2πft）（1-cos（2πfNt）]，其中，f（f =200 kHz）为激励信号中心频率，N（N=10）为单个激励脉冲所含的周波数，t为时间，A（A=0.000 1 mm）为激励脉冲的振幅。更改f和N，可以得到经汉宁窗窗函数调制后的，中心频率为f的汉宁窗函数调制脉冲信号。以中心频率为200 kHz，周波数为10的汉宁窗函数调制脉冲信号为激励信号。该位移激励直接施加在模型的左端，可以激发S0模态Lamb波。模型中设置了19个信号接收点，在距离左端边界150 mm位置处设置第一个信号接收点，随后每间隔100 mm分别设置一个信号接收点。模型网格尺寸为0.05 mm，而所要模拟的波的最短波长大约为2.7 mm，一个波长范围至少含有54个单元，确保了计算精度。图4下半部分所示为在模型左端施加位移激励后某时刻的位移云图，从云图可以粗略判断，波沿传播方向（即[x1]方向）的位移关于铝板中性面对称，即位移规律满足S0模态Lamb波特性。

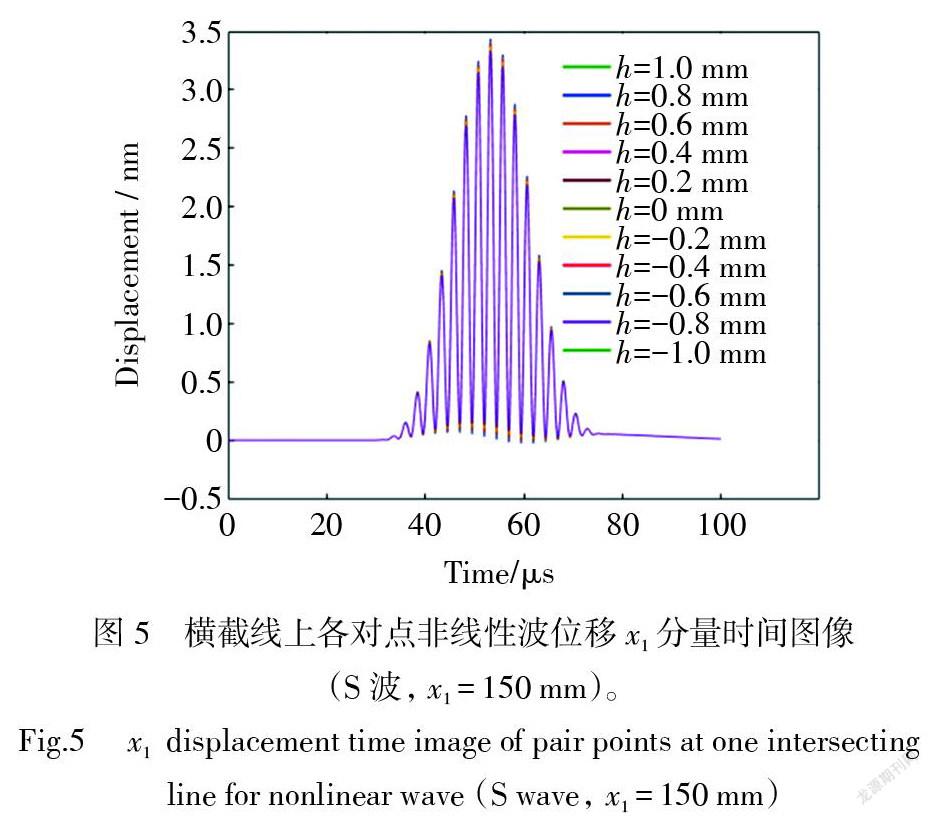
为了验证零频形貌特征，需要将零频从信号中提取出来。为此，我们建立4个模型，分为s和a两组：s组模型激发S波，且这2个模型中，1个模型的初始激励波相位为零，另外1个模型的初始激励波相位为π，即两初始激励波相位相反;a组模型激发A波，同样地，在这2个模型中，1个模型的初始激励波相位为零，另外1个模型的初始激励波相位为π，即2初始激励波相位相反。对于每组模型，在相同位置处接收信号，将相同位置得到的来自于相反相位激励的信号相加。在二次平方非线性作用下，相位为零和相位为π的两个基波激发的非线性波的相位是相同的，而基波的相位刚好相反，于是叠加对应的2个接收信号，可以消除基波，保留零频和二次谐波等非线性波。

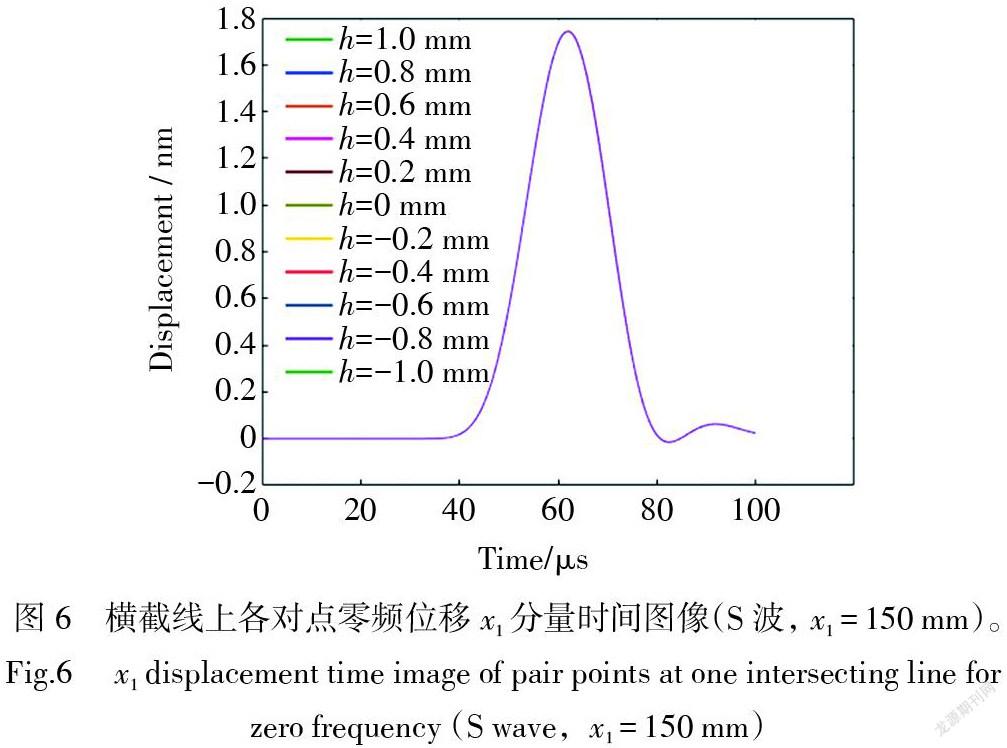
在模型中任意位置划一横截线，即竖线上各点的[x1]坐标相同（150 mm），提取横截线上各点信号，进行分析处理。图5至图6所示横截线的数据图均来自s组模型。其中，图5为通过叠加相位相反的基波得到的非线性波信号，材料非线性具有的二次平方属性导致非线性波为对称模态，横截线上不同厚度位置处质点位移[x1]分量均相同，且二次谐波挂在零频上，或者说零频描绘了二次谐波质点振动的平衡位置。通过对图5中的数据进行低通滤波，滤除高频成分即滤除二次谐波，得到零频的大致形貌如图6所示。图6显示，横截线上不同厚度位置处质点位移[x1]分量完全重合，符合对称模态预期，同时汉宁窗脉冲激励的零频形貌与所加汉宁窗形状相似，与之前理论相符。

对于a组模型，即激励基波模态为反对称模态时，按照与s组相同的步骤分析处理数据，得到的结果与s组结果类似。故对二次平方非线性假设下单频率激励，无论激励Lamb波基波为对称模态还是反对称模态，基波激发产生的非线性Lamb波，主要包括零频和二次谐波，均为对称模态（可参考文献[13， 57]），零频形貌描绘了二次谐波平衡位置的轨迹，与所加窗函数形貌相似。

2.2 零频传播动画

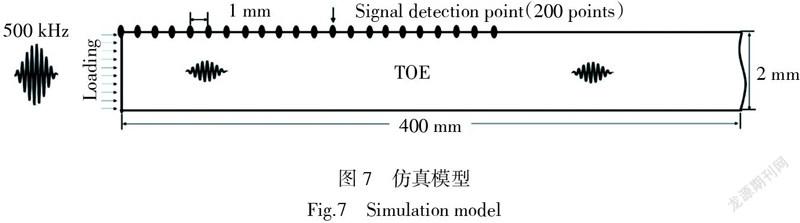
为了一目了然地观察非线性Lamb波随基波传播的演化规律，通过数值仿真和信号处理，制作非线性Lamb波传播规律动画视频。仿真模型与图7所示模型保持一致，为了动画连续性，设置200个信号提取点，且信号提取点之间的间隔为1 mm。为了缩短计算模型长度，必须缩小二次谐波变换空间周期，即需要提高基波频率，设置激励基波频率为500 kHz，通过计算[6]得到二次谐波变化空间距离周期为41 mm左右。图中TOE表示材料参数采用表1中列出的材料参数。

提取所有信号点时域数据，依次播放各点数据，可以得到波随传播距离变化动画;通过反相位相加去掉各点数据含有的基波信号，依次播放各点数据，可以得到非线性波随传播距离变化动画;再通过带通滤波器处理各点数据，依次播放各点数据，可以得到非线性二次谐波随传播距离变化动画;最后通过低通滤波器处理各点数据，依次播放各点数据，可以得到非线性零频随传播距离变化动画。以上动画互动视频可以通过PPT附件“附件-波传播动画视频”查看，从对应动画观看相应信号的传播规律。

2.3 零频可持续累积特性

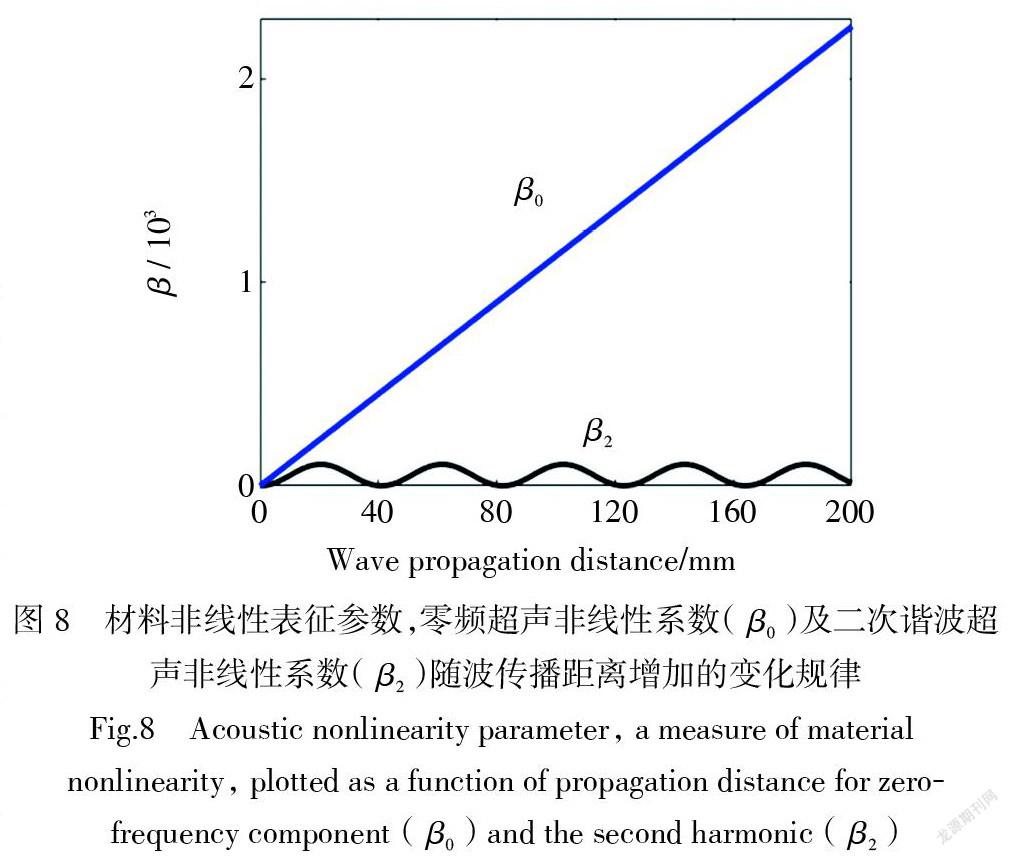
为了得到材料非线性的表征参数即超声非线性系数[β]随基波传播的变化规律，将得到的时域数据进行傅里叶变换，采用零频幅值与基波幅值平方之比定义零频超声非线性系数[β0]，采用二次谐波幅值与基波幅值平方之比定义二次谐波超声非线性系数[β2]。如图8所示，蓝色直线表示零频突破了相速匹配条件的限制，零频超声非线性系数随基波传播距离增加而线性累积;黑色曲线表示二次谐波超声非线性系数受相速匹配条件的制约，随着基波传播距离的增加，呈现周期波动变化规律而无法持续线性累积：符合相关理论预期。

由于基波脉冲激发的零频相位始终相同且在传播过程中保持相位不变，并且零頻具有与S0曲线上频率为零处的相速度相等的相速度[57]，使得传播的基波脉冲前后不同时刻激发的零频脉冲的叠加始终为相长叠加。如果基波群速度和零频群速度不相等，则先后产生的零频不能完全重合，对不同时间产生的零频求和，零频形貌会出现一些新的特征，通常零频会存在一定程度的展宽。如果基波脉冲群速度不相等且具有强烈的色散，基波色散可改变零频形状特征，即随着基波传播不断改变伴随窗函数的形貌，使得零频展现出复杂的形貌特征，但零频相长叠加特性决定了零频随基波传播的无限可累积特性。一般情况下，由于强色散，基波随着传播距离增加，波包数量增多，波包总宽度增宽。截取更多波包，相应的零频超声非线性系数也随之增强，笔者在文献[15]的实验中得到了类似的结果。

3 结论与展望

本文在基波群速度和零频群速度相等以及不考虑色散的情形下，得到了Lamb波脉冲激励零频分量理论解，色散和群速度可影响零频分量最终的形貌，不影响零频分量随着基波传播的持续累积特性，为非线性Lamb波零频分量早期无损健康检测实际应用打下了坚实的理论基础。本文聚焦Lamb波脉冲激励的零频理论研究，主要强调了比较实用的零频可累积特性，同时提供了仿真验证，更多关于零频的仿真结果可参考文献[13，57-58]，实验结果可以参见文献[15，59-60]。

实用中，选择低色散和基波与零频群速度相等（或近似相等）的脉冲激励，无疑会带来极大便利。只需要截取相应的完整波包进行傅里叶变换，用零频幅值与基波幅值平方之比定义的零频超声非线性系数，作为材料损伤指数即可。当所使用的激励信号具有较强色散以及基波和零频群速度不相等时，需要截取更宽的信号进行傅里叶变换，以确保激发的零频均被求和积分。

理论求解中，取两频率相等的极限，便可以得到零频理论解。从求解过程不难理解，除了单频激励之外，还存在同一频率相遇的情况。比如横波先发射，纵波后发射，纵波速度快，在纵波追上横波并与之相遇混合时，是否能够激励混合零频。更进一步地，相同频率以一定角度相遇，是否能够在新的方向上激励出混合零频，甚至不同频率混合后是否能够产生混合零频分量。如果能，零频检测技术将能继承混合波检测技术的优点，实现损伤的定位功能，前景将是诱人的。针对这些问题，研究者已展开相关理论和仿真研究，目前取得了混合波激发零频的初步研究结果。零频检测技术有望继承混频检测技术的优点，实现损伤定位功能，且相关受限条件更少。零频检测技术，在结合二次谐波和混合波优点的同时，能够克服相关缺点，应用潜力巨大，接下来将开展一系列的实验验证研究。

参考文献：

[1]    张剑锋，轩福贞，项延训. 材料损伤的非线性超声评价研究进展[J]. 科学通报，2016，61（14）：1536-1550.

[2]    MEYENDORF N G，RÖSNER H，KRAMB V，et al. Thermo-acoustic fatigue characterization[J]. Ultrasonics，2002，40（1/2/3/4/5/6/7/8）：427-434.

[3]    PALIT SAGAR S，DAS S，PARIDA N，et al. Non-linear ultrasonic technique to assess fatigue damage in structural steel[J]. Scripta Materialia，2006，55（2）：199-202.

[4]    DENG M X. Cumulative second-harmonic generation of Lamb-mode propagation in a solid plate[J]. Journal of Applied Physics，1999，85（6）：3051-3058.

[5]    DENG M X. Analysis of second-harmonic generation of Lamb modes using a modal analysis approach[J]. Journal of Applied Physics，2003，94（6）：4152-4159.

[6]    DE LIMA W J N，HAMILTON M F. Finite-amplitude waves in isotropic elastic plates[J]. Journal of Sound and Vibration，2003，265（4）：819-839.

[7]    DENG M X，WANG P，LV X. Experimental observation of cumulative second-harmonic generation of Lamb-wave propagation in an elastic plate[J]. Journal of Physics D：Applied Physics，2005，38（2）：344-353.

[8]    SRIVASTAVA A，LANZA DI SCALEA F. On the existence of antisymmetric or symmetric Lamb waves at nonlinear higher harmonics[J]. Journal of Sound and Vibration，2009，323（3/4/5）：932-943.

[9]    DENG M X，XIANG Y X，LIU L B. Time-domain analysis and experimental examination of cumulative second-harmonic generation by primary Lamb wave propagation[J]. Journal of Applied Physics，2011，109（11）：113525.

[10]  KRISHNA CHILLARA V，LISSENDEN C J. Interaction of guided wave modes in isotropic weakly nonlinear elastic plates：Higher harmonic generation[J]. Journal of Applied Physics，2012，111（12）：124909.

[11]  HONG M，SU Z Q，WANG Q，et al. Modeling nonlinearities of ultrasonic waves for fatigue damage characterization：Theory，simulation，and experimental validation[J]. Ultrasonics，2014，54（3）：770-778.

[12]  劉瑶璐，胡宁，邓明晰，等. 板壳结构中的非线性兰姆波[J]. 力学进展，2017，47：503-533.

[13]  SUN X Q，DING X Y，LI F L，et al. Interaction of lamb wave modes with weak material nonlinearity：generation of symmetric zero-frequency mode[J]. Sensors，2018，18（8）：2451.

[14]  SUN X Q，LIU X Y，LIU Y L，et al. Simulations on Monitoring and Evaluation of Plasticity-Driven Material Damage Based on Second Harmonic of S Mode Lamb Waves in Metallic Plates[J]. Materials，2017，10 （7）：827.

[15]  SUN X Q，SHUI G S，ZHAO Y X，et al. Evaluation of early stage local plastic damage induced by bending using quasi-static component of Lamb waves[J]. NDT & E International，2020，116：102332.

[16]  MINIACI M，GLIOZZI A S，MORVAN B，et al. Proof of concept for an ultrasensitive technique to detect and localize sources of elastic nonlinearity using phononic crystals[J]. Physical Review Letters，2017，118（21）：214301.

[17]  BERMES C，KIM J Y，QU J M，et al. Experimental characterization of material nonlinearity using Lamb waves[J]. Applied Physics Letters，2007，90（2）：021901.

[18]  BERMES C，KIM J Y，QU J M，et al. Nonlinear Lamb waves for the detection of material nonlinearity[J]. Mechanical Systems and Signal Processing，2008，22（3）：638-646.

[19]  PRUELL C，KIM J Y，QU J M，et al. Evaluation of fatigue damage using nonlinear guided waves[J]. Smart Materials & Structures，2009，18（3）：035003.

[20]  PRUELL C，KIM J Y，QU J，et al. A nonlinear-guided wave technique for evaluating plasticity-driven material damage in a metal plate[J]. NDT & E International，2009，42（3）：199-203.

[21]  LI W B，CHO Y，ACHENBACH J D. Detection of thermal fatigue in composites by second harmonic Lamb waves[J]. Smart Materials and Structures，2012，21（8）：085019.

[22]  XIANG Y X，DENG M X，XUAN F Z，et al. Effect of precipitate-dislocation interactions on generation of nonlinear Lamb waves in creep-damaged metallic alloys[J]. Journal of Applied Physics，2012，111（10）：104905.

[23]  XIANG Y X，DENG M X，XUAN F Z. Creep damage characterization using nonlinear ultrasonic guided wave method：a mesoscale model[J]. Journal of Applied Physics，2014，115（4）：044914.

[24]  XIANG Y X，ZHU W J，LIU C J，et al. Creep degradation characterization of titanium alloy using nonlinear ultrasonic technique[J]. NDT & E International，2015，72：41-49.

[25]  DENG M X，PEI J F. Assessment of accumulated fatigue damage in solid plates using nonlinear Lamb wave approach[J]. Applied Physics Letters，2007，90（12）：121902.

[26]  RAUTER N，LAMMERING R. Numerical simulation of elastic wave propagation in isotropic media considering material and geometrical nonlinearities[J]. Smart Materials and Structures，2015，24（4）：045027.

[27]  WAN X，TSE P W，XU G H，et al. Analytical and numerical studies of approximate phase velocity matching based nonlinear S0 mode Lamb waves for the detection of evenly distributed microstructural changes[J]. Smart Materials and Structures，2016，25（4）：045023.

[28]  SHEN Y F，GIURGIUTIU V. Predictive modeling of nonlinear wave propagation for structural health monitoring with piezoelectric wafer active sensors[J]. Journal of Intelligent Material Systems and Structures，2014，25（4）：506-520.

[29]  WAN X，ZHANG Q，XU G，et al. Numerical simulation of nonlinear Lamb waves used in a thin plate for detecting buried micro-cracks[J]. Sensors （Basel），2014，14（5）：8528-8546.

[30]  DING X Y，ZHAO Y X，HU N，et al. Experimental and numerical study of nonlinear lamb waves of a low-frequency S0 mode in plates with quadratic nonlinearity[J]. Materials，2018，11（11）：2096.

[31]  CROXFORD A J，WILCOX P D，DRINKWATER B W，et al. The use of non-collinear mixing for nonlinear ultrasonic detection of plasticity and fatigue[J]. The Journal of the Acoustical Society of America，2009，126（5）：EL117-EL122.

[32]  DEM[C]ENKO A，AKKERMAN R，NAGY P B，et al. Non-collinear wave mixing for non-linear ultrasonic detection of physical ageing in PVC[J]. NDT & E International，2012，49：34-39.

[33]  JU T，ACHENBACH J D，JACOBS L J，et al. One-way mixing of collinear waves in an adhesive layer [J]. The Journal of the Acoustical Society of America，2019，145（1）：110-113.

[34]  TANG G X，LIU M H，JACOBS L J，et al. Detecting localized plastic strain by a scanning collinear wave mixing method[J]. Journal of Nondestructive Evaluation，2014，33（2）：196-204.

[35]  ZHAO Y X，CHEN Z M，CAO P，et al. Experiment and FEM study of one-way mixing of elastic waves with quadratic nonlinearity[J]. NDT & E International，2015，72：33-40.

[36]  HASANIAN M，LISSENDEN C J. Second order harmonic guided wave mutual interactions in plate：Vector analysis，numerical simulation，and experimental results[J]. Journal of Applied Physics，2017，122（8）：084901.

[37]  JIAO J P，MENG X J，HE C F，et al. Nonlinear Lamb wave-mixing technique for micro-crack detection in plates[J]. NDT & E International，2017，85：63-71.

[38]  ALSTON J，CROXFORD A，POTTER J，et al. Nonlinear non-collinear ultrasonic detection and characterisation of kissing bonds[J]. NDT & E International，2018，99：105-116.

[39]  LI W B，DENG M X，HU N，et al. Theoretical analysis and experimental observation of frequency mixing response of ultrasonic Lamb waves[J]. Journal of Applied Physics，2018，124（4）：044901.

[40]  SUN M X，XIANG Y X，DENG M X，et al. Scanning non-collinear wave mixing for nonlinear ultrasonic detection and localization of plasticity[J]. NDT & E International，2018，93：1-6.

[41]  DING X Y，ZHAO Y X，DENG M X，et al. One-way Lamb mixing method in thin plates with randomly distributed micro-cracks[J]. International Journal of Mechanical Sciences，2020，171：105371.

[42]  HERNANDEZ DELGADILLO H，LOENDERSLOOT R，YNTEMA D，et al. Steering the propagation direction of a non-linear acoustic wave in a solid material[J]. Ultrasonics，2019，98：28-34.

[43]  JU T，ACHENBACH J D，JACOBS L J，et al. Nondestructive evaluation of thermal aging of adhesive joints by using a nonlinear wave mixing technique[J]. NDT & E International，2019，103：62-67.

[44]  ASLAM M，NAGARAJAN P，REMANAN M. Defect localization using nonlinear lamb wave mixing technique[J]. Journal of Nondestructive Evaluation，2021，40（1）：1-12.

[45]  JONES G L，KOBETT D R. Interaction of elastic waves in an isotropic solid[J]. The Journal of the Acoustical Society of America，1963，35（1）：5-10.

[46]  CHEN Z M，TANG G X，ZHAO Y X，et al. Mixing of collinear plane wave pulses in elastic solids with quadratic nonlinearity[J]. The Journal of the Acoustical Society of America，2014，136（5）：2389-2404.

[47]  SUN M X，QU J M. Analytical and numerical investigations of one-way mixing of Lamb waves in a thin plate [J]. Ultrasonics，2020，108：106180.

[48]  ISHII Y，BIWA S，ADACHI T. Non-collinear interaction of guided elastic waves in an isotropic plate[J]. Journal of Sound and Vibration，2018，419：390-404.

[49]  BRILLOUIN L. Sur les tensions de radiation[J]. Annales De Physique，1925，10（4）：528-586.

[50]  THURSTON R N，SHAPIRO M J. Interpretation of ultrasonic experiments on finite-amplitude waves[J]. The Journal of the Acoustical Society of America，1967，41（4B）：1112-1125.

[51]  NARASIMHA K T，KANNAN E，BALASUBRAMANIAM K. Issues on the pulse-width dependence and the shape of acoustic radiation induced static displacement pulses in solids[J]. Journal of Applied Physics，2009，105（7）：073506.

[52]  JACOB X，TAKATSU R，ROYER D. Experimental study of the acoustic radiation strain in solids [J]. Applied Physics Letters，2006，88（13）：134111-134114.

[53]  QU J M，JACOBS L J，NAGY P B. On the acoustic-radiation-induced strain and stress in elastic solids with quadratic nonlinearity （L）[J]. The Journal of the Acoustical Society of America，2011，129（6）：3449-3452.

[54]  QU J，NAGY P B，JACOBS L J. Pulse propagation in an elastic medium with quadratic nonlinearity （L）[J]. The Journal of the Acoustical Society of America，2012，131（3）：1827-1830.

[55]  NAGY P B，QU J，JACOBS L J. Finite-size effects on the quasistatic displacement pulse in a solid specimen with quadratic nonlinearity[J]. The Journal of the Acoustical Society of America，2013，134（3）：1760-1774.

[56]  Sun X Q，Liu X Y，Hu N. Interaction of guided waves in isotropic elastic plates with weak material nonlinearity：sum-frequency，differencefrequency，second harmonic and zero-frequency components[C]. The 9th International Symposium on NDT in Aerospace，Xiamen，China，2017.

[57]  WAN X，TSE P W，ZHANG X H，et al. Numerical study on static component generation from the primary Lamb waves propagating in a plate with nonlinearity[J]. Smart Materials and Structures，2018，27（4）：045006.

[58]  SUN X Q，LIU H J，ZHAO Y X，et al. The zero-frequency component of bulk waves in solids with randomly distributed micro-cracks[J]. Ultrasonics，2020，107：106172.

[59]  DENG M X. An experimental approach for detection of the acoustic radiation induced static component in solids[J]. Chinese Physics Letters，2020，37（7）：074301.

[60]  GAO G J，CHEN H，HU N，et al. Experimental observation of static component generation by Lamb wave propagation in an elastic plate[J]. Ultrasonics，2021，117：106537.

[61]  LANDAU L D，LIFSHITZ E M. Theory of elasticity [M]. Pergamon Press，1959.