离心场下大径向负载液体静压轴承设计与实验

吕 磊，舒 杨

（中国工程物理研究院总体工程研究所，绵阳 621900）

0 引言

精密离心机是通过转臂/转盘的高精度回转运动从而产生具有较高精度离心场的精密设备，它是惯性导航仪表、大量程精密加速度计等设备仪器性能实验与精度标定的重要计量设备［1⁃3］。 惯性导航器件性能的飞速发展对精密离心机设备提出了更高精度、更大回转半径、更大负载容量等诸多要求，尤其是在离心机转臂末端即高离心场中，安装有同步反转平台的双轴精密离心机［2，4⁃5］对惯性捷联惯组导航器件的测试与标定发挥着核心作用。

液体静压轴承借助于支承运动副间形成的润滑油膜来承担载荷，实现了轴承的近零摩擦、无磨损、长寿命，加之液体介质对轴承零部件工作面的误差均化效应，使得静压主轴能够达到较高的运动精度。同时，相对于气体静压轴承，液体静压主轴由于工作介质不易被压缩而工作稳定性更高，在一定条件下更能满足大承载力的需求。鉴于上述优势，静压支承技术广泛应用于精密、超精密以及重载设备中。

目前，精密静压主轴、轴承已在精密离心机设计中得到了一定程度的研究和应用。研究中指出［4⁃5］，国外精密离心机在主轴和从轴轴承上都有采用气体静压轴承的先例。在国内，陈磊等［6］就精密离心机主轴采用的液体静压轴承展开了设计与研究。针对精密离心机用液体静压主轴系统轴承研损故障，刘洪丰等［7］对设计、装调过程中的问题进行了详细分析。李树森等［8］则对精密离心机静压气体轴承主轴系统的稳定性进行了分析，通过数值仿真得到气体静压轴承的稳定域。针对精密离心机气体轴承⁃转子耦合系统，杜平安等［9］计算了径向、止推轴承的非线性承载力模型，分析了主轴回转精度，并探讨了主轴回转精度对精密离心机精度的影响。对于液体静压轴承，尽管发展年代较早，但一直以来仍有较大的研究空间。Nataraj等［10］研究了计及流体惯性时液体静压轴承的刚度、阻尼等特性。Bakker等［11］研究了液体静压轴承中的均压腔深度对环状止推轴承性能的影响。Braun等［12］定性定量地深入探讨了液体静压轴承均压腔内流场的特性。Dzodzo等［13］研究了液体静压轴承均压腔及其截面突变位置处的流体压力与流动特性。Kakoty等［14］应用线性扰动方法分析了流体的惯性效应对液体静压轴承的稳定性问题。

尽管目前国内、国外已对精密离心机用的主轴从设计、分析、实验、测试等诸多方面展开了一定的研究，并将研究成果广泛应用于工程之中，但是对于双轴精密离心机而言，对位于精密离心机转臂末端的从轴轴承的系统性研究仍十分匮乏。在动态离心场作用下，位于离心场中的从轴静压轴承将持续受到大小随离心机转速变化、方向相对离心机转臂恒定的负载载荷的作用。同时，随着需求的不断提高，精密离心机所需提供的离心场大小越来越大，导致位于离心场中的静压轴承在径向上受力愈发严酷，逐渐成为精密离心机设计研发中的瓶颈。本文针对高离心场下工作的大负载液体静压轴承设计展开讨论，结合仿真分析与实验研究对液体静压轴承性能及相应结构设计进行了分析。

1 非对称式静压轴承设计分析

1.1 设计输入分析与讨论

离心场静压轴承主要技术指标如表1所示，双轴精密离心机原理如图1所示。

表1 离心场静压轴承主要技术指标Table 1 Main technical indexes of hydrostatic bearing in centrifugal field

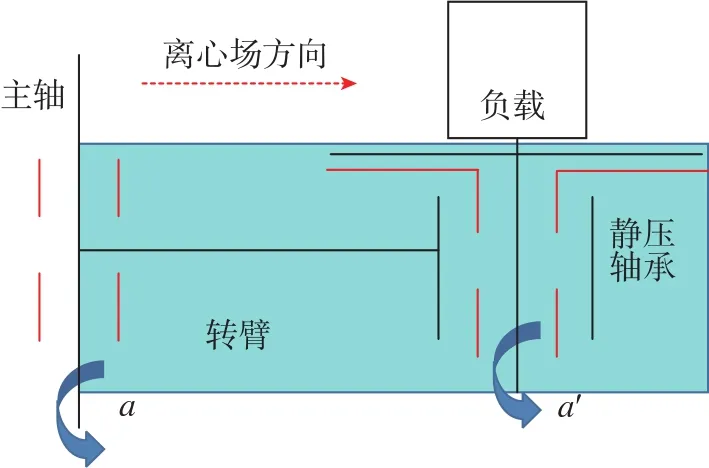
图1 双轴精密离心机示意图Fig.1 Schematic diagram of double⁃axis precision centrifuge

主轴a以角速度ω旋转，带动转臂旋转。静压轴承安装在转臂末端，整体随转臂旋转。正常工作时，置于静压轴承上的被测试件以及静压轴承自身转子都将受到离心力的作用，成为静压轴承的径向负载。负载大小与此时的离心场（即与主轴a的转速）大小有关，而方向恒定为沿转臂方向向外。

离心场静压轴承沿转臂方向受力为

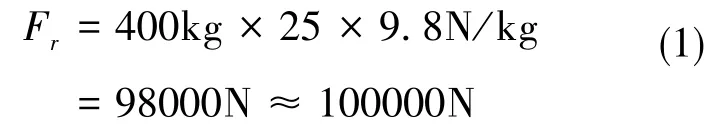
静压轴承沿轴向受力为

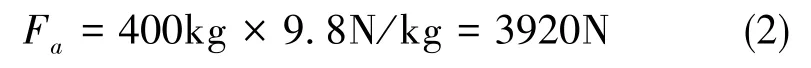
可以看出，静压轴承在轴向上受力很小，易于达到；而轴承径向上则需要承受约100000N恒定方向的作用力，远高于轴向受力。因此，本文后续将重点讨论静压轴承的径向轴承设计与分析，止推轴承设计分析本文中不再赘述。

1.2 液体静压主轴结构形式分析

液体静压轴承在离心场下正常工作时，轴承将受到大小随转速变化、但方向恒定的作用力。一般应用工况下的静压轴承设计中，径向承载的油膜单元往往在周向均匀、对称布置，并且每个轴承承载单元的结构形式、尺寸大小都相同，都供给相同压力的液压油，从而在理论上，当转子位于中心时，这些承载单元产生的承载力和承载刚度都是相同的。当轴承沿径向产生外力负载时，依靠承载单元的油膜在有限范围内的厚度变化引起各个油膜面承载力大小的变化；轴承在径向上各个单元油膜面承载力的合力综合形成轴承的径向承载力，起到平衡外力的作用。

在不考虑供油压力调节、不考虑轴承承载单元更改时，静压轴承的径向承载能力仅受到油膜厚度变化的影响。然而在工程上，液体静压轴承承载单元的油膜厚度（单侧）通常在20μm～50μm之间。油膜厚度小于20μm时，油膜厚度过薄，轴承易抱轴，不利于轴承安全；而油膜厚度大于50μm时，油膜的承载力和承载刚度往往将显著降低，且导致轴承回转精度一定程度地降低，轴承综合性能不理想。为保证一定的回转精度，静压轴承油膜厚度也将控制在一定范围内。

因此，结合静压轴承设计［15⁃16］分析，在有限的油膜厚度范围内，要求独立的某一油膜面在上述膜厚范围内达到不小于100000N的承载力变化量，且仍保持较高的回转精度，在其余条件不发生改变时有较高的实现难度。因此，针对高离心场下静压轴承的大径向载荷，需要对径向轴承进行非对称式的结构设计与分析，以求达到设计要求。

由于静压轴承在高离心场下使用，需要轴承承载单元为轴承提供非对称的径向承载能力。根据静压支承原理［15⁃16］，大致具有以下三种途径：

1）采用不等面积（包角）的油膜面设计；

2）等油膜面、不等面积均压腔；

3）各轴承承载单元独立供油，根据设计需要供给不等压力的液压油。

原理上，既可以独立也可以联合采用以上三种非对称的设计方式，图2为采用不等油膜面、不等均压腔设计的轴承结构示意图。

图2 非对称结构形式的轴承示意图Fig.2 Schematic diagram of asymmetrical bearing

2 非对称式静压轴承性能计算与分析

2.1 周向6组油膜设计

设计如图3所示形式的径向轴承：Film⁃1面周向包角80°，均压腔采用矩形腔室结构，包角40°；Film⁃2面周向包角40°，矩形均压腔包角20°；其余各面尺寸一致，周向包角60°，矩形均压腔包角30°；径向轴承的直径为300mm。为简化说明，下文中将主要提供承载力的单元Film⁃1称为主承载单元，其余承载单元统称为辅助承载单元。

图3 周向6组非对称油膜面设计的轴承截面示意图Fig.3 Schematic diagram of bearing section with asymmetrical 6 oil⁃film pads

如图3所示，每组油膜面都将形成承载力，其方向如图中箭头所示，轴承径向合力则提供轴承整体的径向承载能力。由于油膜面尺寸、角度已经确定，故轴承径向合力可由下式给出

式（3）中，Wi为对应i油膜面的承载力。静压轴承设计拟采用46＃液压油，利用Fluent对油膜面流场进行计算仿真，得到的油膜面承载力如表2所示。

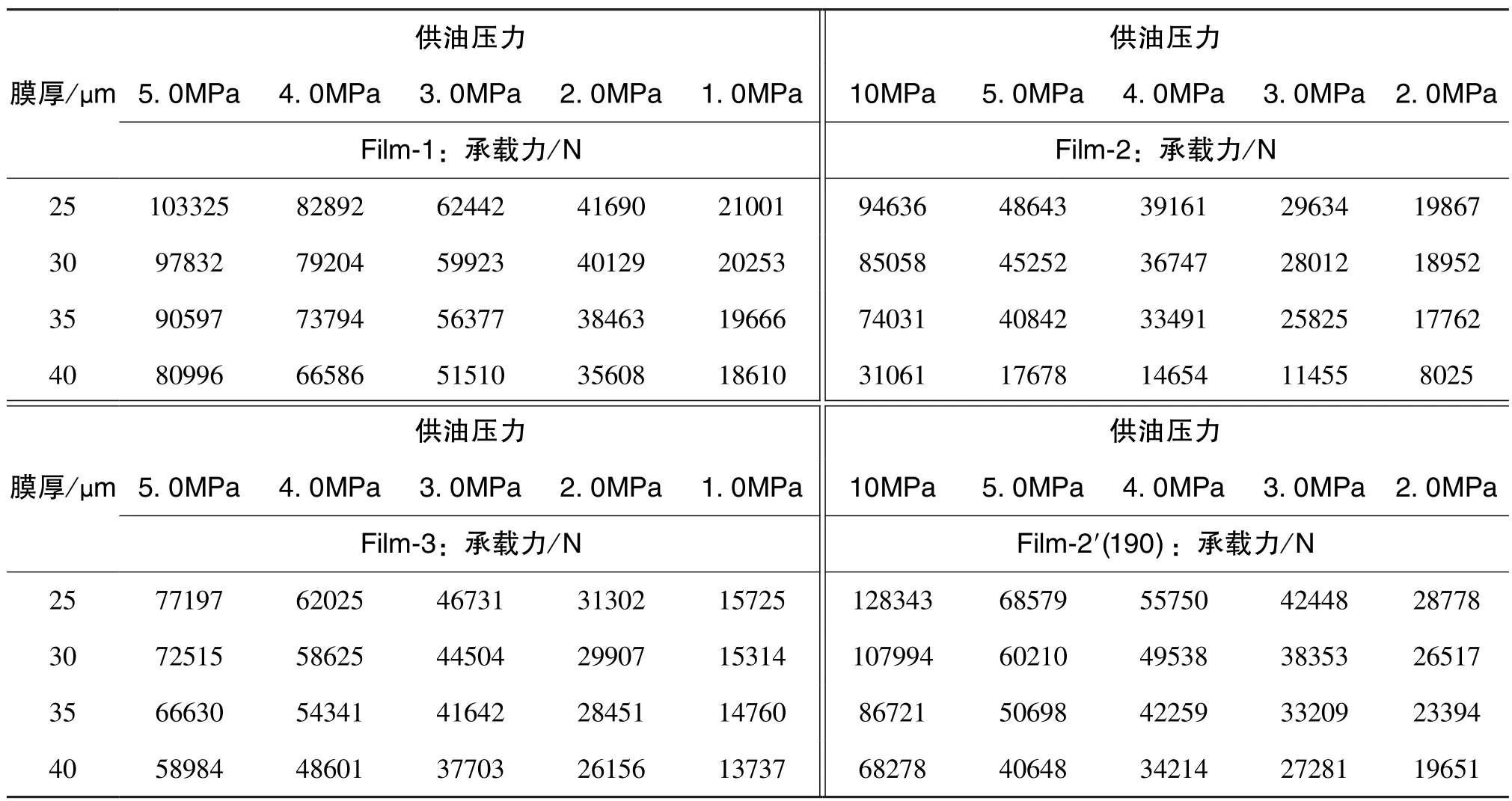
表2 油膜面承载力CFD计算值Table 2 Results of load⁃carrying capacity of oil⁃film pad by CFD

将表2的数据带入式（3）中，轴承间隙按照25μm取值时，供油压力全部为2MPa，此时得到的合力大小仅为4722N，方向向右。当Film⁃2′面采用大均压腔（h190）时，非对称承载力（合力）可达到约13633N，承载力有效提高。尽管如此，当采用反轴承单边支承，轴承轴向上布置2套径向轴承，承载力也远达不到所需的100000N。当Film⁃2面采用独立高压力供油时，计算可知：10MPa时，合力达到98453N，接近达到100000N的承载力要求。因此，实际供油压力需达到约11MPa才能满足要求。

通过上述分析可知，尽管Film⁃1面等效面积较大，但实际考虑合力因素时，其提供的承载力是相对较小的。在保证设计要求的前提下，在此基础上以减小供油压力为目标，减小Film⁃1面的均压腔面积，并采用 “H”型均压腔以保持油膜面持续供油及其承载刚度。采用的 “H”型均压腔轴承结构如图4所示。

图4 “H”型均压腔示意图Fig.4 Schematic diagram of the H⁃shaped pressure equalizing chamber

“H”型是常用的大油膜面均压腔设计形式之一，它的主要优势在于：如果运用在较大油膜面的轴承中，可在实现保持不显著扩大均压腔面积、增大流量的同时，增大油膜面承载力和刚度。将较大油膜面均压腔修改为 “H”型结构后，Film⁃1面的承载力数据如表3所示。

表3 改为“H”型后的油膜面承载力CFD计算值Table 3 Results of load⁃carrying capacity of oil⁃film pad by CFD after changing to “H”type

对比可知，在优化大油膜面均压腔结构形式后，其余边界条件不变时，“H”型均压腔能有效减小顽抗力，同时满足整个油膜面的有效供油。根据表3的计算结果，当Film⁃2面供油2MPa时，合力提高至112506N，满足设计承载力需求。

因此，相比之下，在调整Film⁃1面的均压腔结构形式有效降低承载力之后，轴承径向合力有显著提高。

小结周向6组油膜设计方案发现，当前设计条件下，主承力面需要10MPa供油压力才能基本满足轴承径向承载力要求。通常而言，即使重载液体静压轴承，稳定工作时的供油压力通常约为4MPa，一般不超过6MPa。

不采用过高的油压，认为有以下几点原因：首先，油压过高，供油压力稳定度不高，供油压力的波动将导致轴承精度降低，此时可以通过提高精密液压站的性能获得改善；其次，高油压易加剧液压油发热，油液性能尤其是黏性与油温息息相关，黏度大小又直接关系到轴承的承载力和刚度，油温显著升高，则黏性急剧下降，承载能力降低，同时，液压油温升会将热量传递到轴承和转子等结构件上，导致轴承发生热弹性变形，造成外圆工作面变大，内圆工作面缩小，极易导致轴承抱轴的严重事故；第三，实际工程应用中，过高的油压还将引起供油管路的耐压及安全性问题，考虑到管路同样在一定g值的超重力离心场下工作，耐压管路安全性问题更值得重视；最后，过高的油压也将使整个供油系统线路中的所有接头面临更严酷的密封挑战，尤其是当密封部位在超重力环境下，超重力场导致的密封原件受到特定方向的作用力时，密封性能将会明显降低，极易造成油液渗漏。因此，在实际工作中，通常不给轴承供给过高压力的液压油。

2.2 周向5组油膜设计

对于数量为偶数的油膜面，受力方向上大小面对立的设计思路进一步深化，可得到小油膜面为包角0°的情况，形成奇数组油膜面的设计方案。

径向承载单元周向共计奇数组，可以有3组、5组和7组三种不同的方案。周向3组承载单元，则每组单元均分则有包角120°，每组承载面面积较大，考虑到轴承周向回转的承载力均匀性，3组单元分布的方案则数量较少。周向7组的方案则由于轴承确定设计内径为φ300mm，使得每组单元面积过小。综合考虑，本文采用周向5组承载单元分布的方案。

设计如图5所示形式的径向轴承：Film⁃1面周向包角72°，均压腔采用矩形腔室结构，包角36°；Film⁃2面周向包角72°，矩形均压腔包角36°；径向轴承的直径为300mm。

图5 周向5组非对称油膜面设计轴承截面示意图Fig.5 Schematic diagram of bearing section with asymmetrical 5 oil⁃film pads

根据假设，5组油膜面在周向均布，结构形式相同，每个油膜面提供的承载力W是相同的，则轴承径向合力为

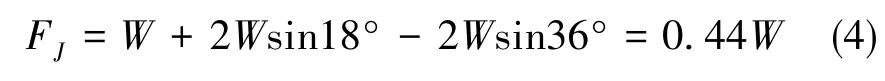
可知，当采用完全相同的奇数组油膜面布置时，轴承可在所需方向上提供0.44倍承载力。油膜面承载力在Fluent中的计算结果如表4所示。

表4 周向均布的5组油膜面各面承载力（5个面大小相同，压力不同）Table 4 Results of load⁃carrying capacity of 5 oil⁃film pads（same pads，different supply pressures）

由表4可知，当5组油膜面相同供油压力时，取油膜厚度 25μm，10MPa供油压力，可达到96183N的径向合力，但仍无法满足要求。因此，需考虑主承力面（主承载单元）和其余承载力面（辅助承载单元）分别供给压力油的方案。

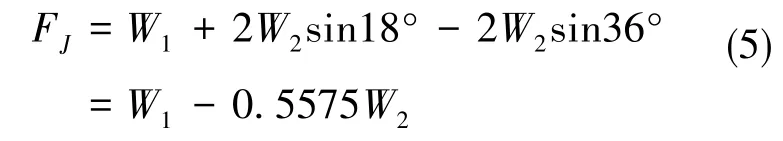
依据表4所列计算结果，当主承载单元采用4MPa、其余4个面采用2MPa供油工作时，轴承径向承载合力达到65214N；主承载单元取5MPa时，轴承径向承载合力为87163N；主承载单元取6MPa时，轴承径向承载合力达到108790N，刚好达到设计要求。

相比周向6组布置的油膜面，5组布置方案已经能够将最高供油压力从10MPa显著降低至6MPa，具有明显优势。但通常而言，对于液体静压主轴，6MPa的最高供油压力仍超出常规使用的压力范围。在运转过程中，即使轴承稳定工作转速不高，也将产生液压油发热黏性降低、承载力下降的情况，并导致轴承的节流器、转子等结构件发热，引起抱轴等突出问题及事故。

为此，主承载单元的均压腔包角修正为50°、均压腔高度修正为200mm，承载单元包角72°保持不变，得到如表5所示的不同供油压力、不同油膜厚度下的主承载单元承载力数值。

表5 周向均布的5组油膜面各面承载力（5个面大小不同，压力不同）Table 5 Results of load⁃carrying capacity of 5 oil⁃film pads（different pads，different supply pressures）

主承载单元按表5所列数据，取值供油压力达到4MPa，其余面按表4所列数据，供油压力2MPa，由式（5）可知，轴承径向承载合力可达98770N；主承载单元取5MPa时，达到128551N的合力，远超出实际所需的100000N。因此，实际只需要大于4MPa、不到5MPa的供油压力，即可满足轴承服役承载力要求。

上述主承载单元的工作供油压力实际上已经落入较为常用的液体静压主轴供油压力范围内，相比大于6MPa或者6组油膜方案中的10MPa最高供油压力，已能在满足要求的前提下有效解决了轴承因高压油发热而导致的系列问题。

2.3 不同油膜厚度下的承载力

由于仿真（网格数一般不小于1400万）计算量较大、耗时较长，且油膜承载力是供油压力和油膜厚度变量的连续、可导函数，出于时间和经济性考虑，不需要对承载单元的每个供油压力和每个油膜厚度都进行仿真计算，只需要计算出大部分参数节点处的数值即可（在所需的压力、油膜厚度处的承载力通过2次多项式插值获得）。根据Fluent计算得到主/辅助承载单元的承载力结果，拟合其关于供油压力、油膜厚度和承载力的曲面，如图6所示。

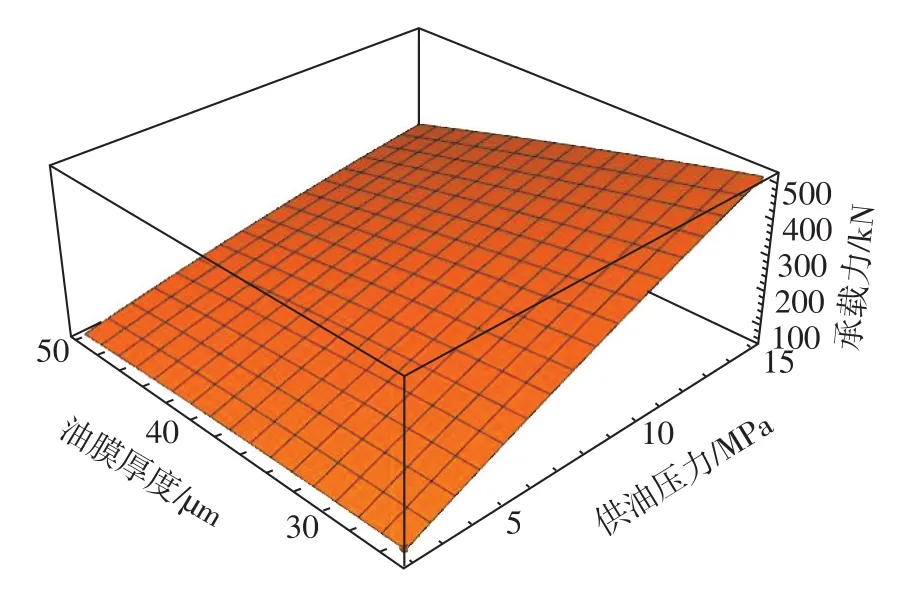
图6 不同供油压力、油膜厚度下的主承载单元承载力拟合曲面Fig.6 Curved surface fitting for load⁃carrying capacity of the main bearing unit under different oil supply pressure and oil film thickness

3 实验研究

3.1 实验设备与方案说明

如图7所示，基于上述理论与仿真分析研究开展了相关实验，研制了用于实验验证的液体静压轴承以及用于模拟径向离心场载荷的径向加载系统。

图7 实验用液体静压轴承及径向加载系统Fig.7 Hydrostatic bearing and radial loading system for experiment

实验系统主要由静压轴承、精密液压站及冷却系统、液压缸和加载系统组成。精密液压站为液体静压轴承提供压力油，轴承安装于机座上，机座和液压缸支架、底板共同作为径向加载系统固定连接在一起，两套液压缸通过加载杆同时作用在静压轴承上，向轴承施加径向载荷以模拟轴承在离心场下工作时所受到的载荷。

液压站输出的液压油需要经过较长的管道及若干分流阀块才能进入轴承，最终到达承载单元的均压腔和油膜面上，因此压力必然存在较大的沿程损失。为监测轴承均压腔内的真实供油压力，在轴承均压腔内开设了压力传感器安装的接口。同时，对上述设计内容进行定量验证还需要对轴承内的油膜厚度（轴承与转子之间的间隙）进行准确测量，因此还需要在轴承承载单元上开设电涡流位移传感器的安装接口。静压轴承承载单元内开设的压力、位移传感器安装接口如图8所示。

图8 静压轴承压力/位移传感器布置示意图Fig.8 Layout diagram of hydrostatic bearing pressure/displacement sensor

如图9所示，本实验主要针对静压轴承的径向承载能力，两组相同的液压缸为轴承提供0t～10t的载荷作用，通过力传感器测量并记录载荷大小。在液压缸施加作用的同时，实时监测与记录轴承均压腔内的油压和轴承油膜厚度。精密液压站可对轴承提供具有较高压力稳定精度的液压油，还可对油液进行冷却。

图9 液体静压轴承径向承载力测试实验示意图Fig.9 Schematic diagram of hydrostatic bearing radial bearing capacity testing experiment

3.2 实验测试内容与数据分析

（1）液体静压轴承的空载测试

加载测试前，首先开展了液体静压轴承的空载测试，定性探讨轴承规律，并定量地与仿真结果进行对比验证。

图10为空载下调整轴承径向承载单元的供油压力时轴承上电涡流传感器测得的轴承转子在轴承内孔中的平移运动曲线。当关闭轴承主承载单元（上文中的Film⁃1）的供油，其余辅助承载单元（Film⁃2～Film⁃5）持续供油，转子被顶向轴承内孔中的左极限位置（主承载单元一侧），该极限位置一侧没有建立起油膜，通过手动推动也可证实此时转子已与轴承内表面贴合。同理，当打开主承载单元供油、关闭其余辅助承载单元供油时，转子移动到轴承内孔中的右极限位置（远离主承载单元一侧）。依据仿真计算结果，当轴承主承载单元和辅助承载单元供油压力调节合适使之形成的合力为0时，转子处于轴承内孔的中心位置。

根据式（5），轴承一旦制造完成，其所具有的油膜厚度就已经确定。而实际上，轴承可以在多种不同的主承载单元⁃辅助承载单元的供油压力配合作用下实现转子位于中心位置，以某次测试结果为例：

油膜厚度为 2Δ＝68.4μm，Δ≈34μm。 参考2.3节中的仿真计算结果，对34μm厚度下的承载力插值求取，有：W1＝142652N、W2＝273382N，代入式（5）有：F＝ -9848N（合力）、F/W1＝ 6.9%（误差）、F/W2＝3.6%（误差）。 考虑到测试误差的影响，当前得到的仿真计算结果误差是可接受的。

类似，选取另一次测试结果，油膜厚度为2Δ＝67μm，Δ≈33.5μm。当转子位于轴承中心没有偏心量时， 有：W1＝145684N、W2＝ 276306N、F＝-8357N（合力）、F/W1＝5.74%（误差）、F/W2＝3.02%（误差）。

若根据力平衡关系W1＝W2，反算转子左右两侧油膜厚度，有：Δ1≈32.6μm、Δ2≈34.4μm，相差（即转子偏心）约1.8μm，偏心量误差约5.37%。

综上，空载下测试结果与仿真对比显示，仿真计算结果误差一般小于10%。

（2）液体静压轴承的径向加载测试

加载测试过程中，通过精密液压站对加载液压缸工作压力进行调节，从而输出所需的作用力。液压缸与加载测试杆之间加装有称重传感器，测试实时输出的作用力大小。加载过程中实时监测转子位移量、作用力和转子位移实测值，通过数据采集系统实时采集并保存至计算机中。典型的轴承径向加载测试实验结果如图11所示，图11（a）为液压缸加载力输出曲线，图11（b）为主承载单元上安装的电涡流传感器测得的转子位移曲线。

表6和表7为某两次径向加载测试所得到的结果。

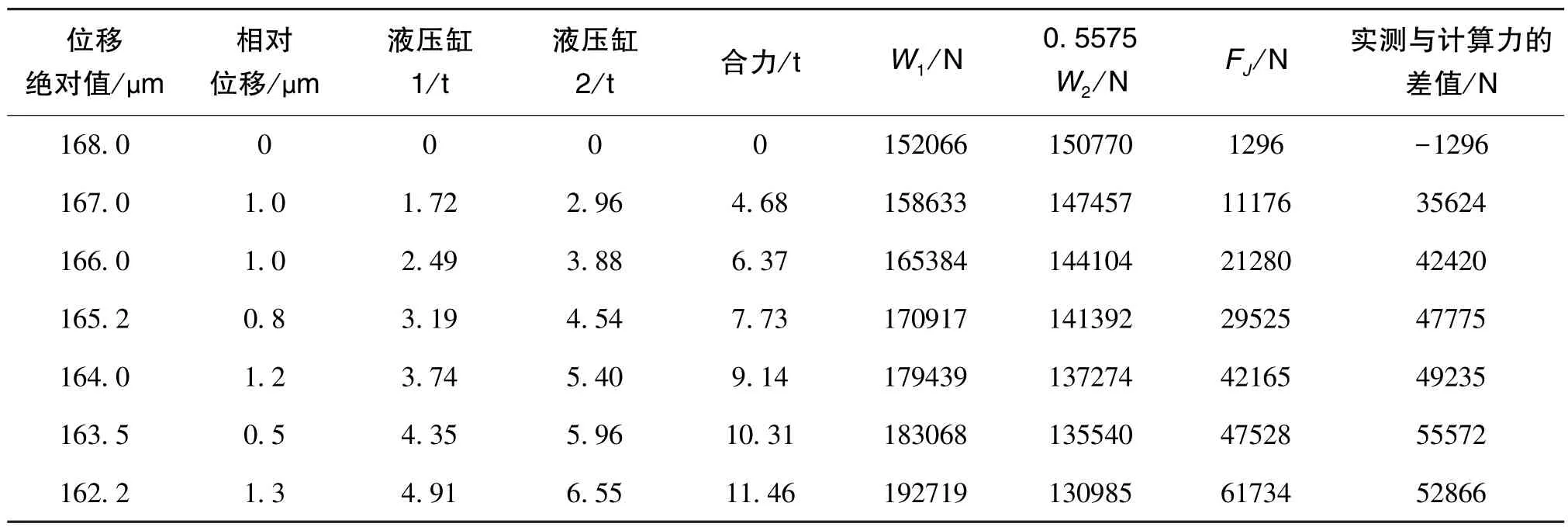
表6 径向加载测试结果1Table 6 Results of radial load experiment 1

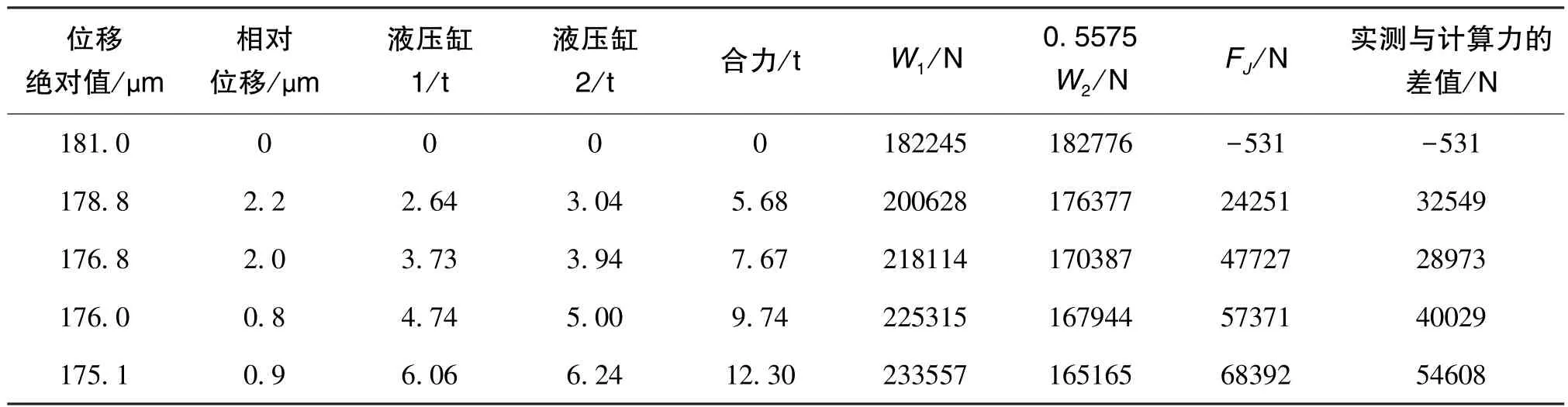
表7 径向加载测试结果2Table 7 Results of radial load experiment 2

对比分析表6、表7中加载测试结果与仿真分析结果的数据，可以得到如下结论：

1）加载至2个液压缸总共输出约12t的拉力，此时显示径向承载单元的油膜仍有较大的厚度。

2）实测结果的承载力比仿真计算的承载力大，最高时实测结果大于计算结果约67%，且多次测量都有实测＞计算的情况（有载荷作用下承载力实测＞计算，是有利于工程实践的结论）。

3）根据测试结果，若转子在加载过程中倾斜，会导致径向油膜一定程度变为楔形，但是均压腔内压力的测试结果仍与仿真计算较为符合。另外，对比表6、表7中所列测试数据可得，在2套液压缸输出作用力差值较小（＜0.5t）时，转子发生相对较大偏移时的计算误差仍相对较大，因此可以认为：对于径向承载单元，在测试过程中的倾斜幅度较小，对仿真计算结果影响不大。

4 结论与展望

针对双轴精密离心机在转臂末端的位于高g值离心场中的液体静压轴承的径向承载力需求，本文开展了液体静压轴承的设计分析与实验研究。针对离心场下受力方向恒定、大小变化的特点，创新且针对性地对径向轴承进行了周向偶数组和奇数组的非对称式油膜面设计，采用非对称的油膜面、均压腔、供油压力方式实现了设计指标。为降低所需的最高供油压力，通过修正均压腔结构尺寸和调整供油压力达到设计目标。

对比分析周向6组和周向5组油膜面的设计可以发现：由于5组油膜布置方案可以保持一个油膜面合力指向与离心场指向一致，该油膜面作为主承载单元能够提供很大比例的承载力贡献，同时该油膜面受到其余面承载力分量的抵消较少，因此在相对较低的供油压力下，5组油膜面即可满足承载力需求。而在离心场方向上，周向6组设计的轴承总是存在一对方向相反的油膜面，其承载力合力将受到较大相互抵消作用，因此周向6组油膜的方案需要提供较高压力的液压油才能满足承载需求。由此，可以认为：5组油膜是6组油膜在离心场方向上成对油膜中小油膜面极限化的结果。

通过合适的结构设计和调整有效降低最高供油压力，可以降低液压油和轴承的温升、减小液压油泄漏率和液压站功耗并在一定程度上保证管路系统的安全。因此，本文除了满足轴承的径向承载力基本要求，还将降低供油压力作为重要设计指标进行了分析和讨论。

根据设计方案，研制了一套实验用液体静压轴承，并配套设计了用于对轴承进行施加径向载荷的加载系统。首先进行了轴承空载下的实验测试，实现了径向承载单元压力调节下转子在轴承内孔中的平移运动，定性探讨轴承规律，并定量地与仿真分析结果对比，得出计算误差较小的结论。其次，开展了径向加载测试，对比仿真计算结果，该实测结果误差相对较大， “实测结果＞计算结果”的结论从工程上讲是有利的。

实测结果与理论计算结果误差较大，经分析，与实验用的2套液压缸出力差值无关。转子偏离平衡状态的 “零位”越大，理论计算误差越大。分析预估，转子偏离理论中心 “零位”越大，各侧油膜横截面的理论形状越接近月牙形，两侧出口处膜厚小于实测值，而中心处膜厚为实测值，呈月牙形，不再是规则的扇形，因此产生了误差。未来研究中，可根据实际工况丰富并完善理论计算模型。

最后，在地面真实模拟离心场这样一种场的作用环境是很困难的，本研究中设计的地面实验并不能完全模拟离心场下液体静压轴承的真实受力情况。因此，后续将进一步开展液体静压轴承的离心场实验研究。