一种基于离心机试验的MEMS IMU加速度计误差建模方法

王国栋，阎 璐，王振凯，宋健民

（北京航天控制仪器研究所，北京 100039）

0 引言

微机电惯性测量单元（MEMS Inertial Measure⁃ment Unit，MEMS IMU）广泛应用于航天、航空、导弹等武器装备领域，加速度计作为速度、位置测量的核心仪表，决定着各类载体的导航精度和使用性能。MEMS IMU在高g条件下，加速度计的输出模型往往表现出高阶、非线性的特征［1］，加速度计模型的精度和符合性是其可靠工作的关键。加速度计在仪表组装成IMU之后，由于受到焊接应力等的影响，在单表阶段标定的模型会发生一定程度的变化，需要重新进行误差建模和补偿。离心机作为高精度的惯性试验设备，可以用来产生高g输入激励［2⁃4］，是进行 MEMS IMU 加速度计误差建模的常用设备。同时，离心机试验过程中引入的各种误差也将影响加速度计模型的精度和误差补偿效果。

目前，领域的研究主要围绕基于离心机试验开展单表层面的加速度计标定测试与误差补偿，没有针对MEMS IMU系统级三轴MEMS加速度计开展相关的建模与补偿研究。本文提出了一种MEMS IMU三轴加速度计高加速度条件下的误差建模与补偿的完整方法，包括试验编排设计、模型参数识别、模型优化与验证等，能够为MEMS IMU加速度计的高精度应用提供技术基础，具有一定的工程应用价值。文中将分析离心机试验引入的各类误差源及误差补偿方法，设计合理的试验方案，并对建立的误差模型进行优化和有效性验证。

1 精密离心机及其误差源

离心机有多种类型，包括双轴长臂离心机、单轴盘式离心机等，本文将会重点分析单轴盘式离心机。单轴盘式离心机试验引入的误差主要包括半径误差、安装失准角误差、回转轴线误差等［5⁃6］。

1.1 半径误差

离心机的半径误差包括静态半径误差和动态半径误差两项。

静态半径误差是指离心机的旋转轴到加速度计的敏感质量块之间的距离测度误差。对于MEMS IMU而言，由于加速度计位于结构件之内，实测法过于复杂，因此通常采用反算法［7］予以求解得到。在计算过程中，静态半径不可避免地产生一定的误差。例如，当水平面内径向安装的加速度计存在0.05mg的输出误差时，半径为0.5m的旋转圆盘产生的半径误差为2.8×10-5m；当产生的向心加速度为20g时，产生的输入误差为1mg。为了减小半径误差，需要提升MEMS IMU在1g条件下的测量精度。静态半径的计算公式为

式（1）中，Er为离心机旋转时的输出平均值，Es为离心机静止时的输出平均值，ω0为离心机旋转时的角速率，ΩV为地球转速的垂向分量。当处于北半球的离心机顺时针旋转时，科氏加速度对应的项2ω0ΩV前面的符号为正；离心机逆时针旋转时，科氏加速度对应的项2ω0ΩV前面的符号为负。

动态半径误差是指离心机在转动过程中由于台面拉伸产生的误差。由于单轴盘式离心机结构紧凑，台面刚度大，动态旋转情况下变形小，因此动态误差较小，可以忽略。

1.2 失准角误差

失准角误差包括水平失准角误差和垂直失准角误差。

理想情况下，MEMS IMU在离心机上安装完成后，MEMS IMU在水平面内的某一加速度计敏感轴将与安装基准面的法向重合。但实际情况下，加速度计敏感轴与安装基准面的法向存在着一定的偏差。水平失准角误差就是指处于径向的加速度计敏感轴与离心机半径方向的夹角，如图1所示。

图1 水平失准角示意图Fig.1 Diagram of horizontal misalignment angle

失准角产生的原因主要有MEMS IMU在离心机上的安装误差、离心机上的安装靠面基准误差等。安装误差是跟MEMS IMU的基准面精度、安装操作、结构变形等因素有关的误差，为了减小安装误差的影响，利用1g条件下的系统三轴输出，反算求得水平失准角

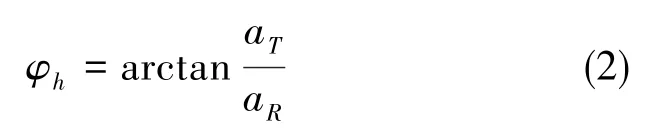
式（2）中，φh为水平失准角，aT为水平切向加速度计输出，aR为水平径向加速度计输出。由于径向敏感的加速度计在MEMS IMU中的位置无法保证处于离心机垂向安装基准面的中心位置，因此会产生水平失准角，该失准角可通过式（2）进行计算得到。当φh为0.1rad、离心机输入的向心加速度为20g时，产生的加速度计敏感轴误差为0.03mg，垂直于径向的敏感轴产生的加速度分量为0.035g。因此，需要通过标定水平失准角对MEMS IMU的输出进行修正。

垂直失准角是指安装基准面的法线与水平面的夹角，垂直失准角的计算公式如下

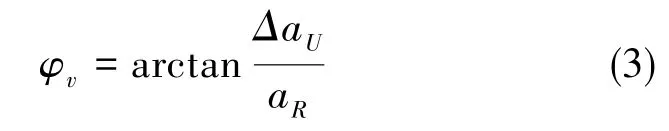
式（3）中，φv为垂直失准角，ΔaU为垂向加速度计的输出误差。由于离心机安装台面和MEMS IMU的安装基准面精度均较高，因此垂直失准角较小，可以忽略。

1.3 回转轴线引起的垂直度误差

当离心机的回转轴线与铅垂线不平行时，会在MEMS IMU加速度计的水平输入轴上引入重力加速度分量

式（4）中，ar为重力加速度的水平分量，γ为离心机回转轴线与铅垂线的夹角，ω为离心机的转速。由式（4）可知，ar的大小随着离心机的转动呈现出周期性变化。因此，通过采集整周转动周期数据取平均值，可以消除离心机回转轴线垂直度引起的误差。

2 离心机试验编排

2.1 MEMS IMU安装位置

MEMS IMU的安装位置取决于需要估计的模型系数。对于MEMS加速度计来说，敏感轴的一次项、二次项以及交叉轴的一次项、二次项影响较为突出，交叉耦合项影响较弱。因此，设计的安装位置为MEMS IMU三个敏感轴的正负向，共计有6个，如图2所示。通过位置1～位置6的测试，能够得到不同情形下的MEMS IMU三个敏感轴向的加速度输入。位置1、位置2主要用于激励产生X+、X-向的加速度输入，位置3、位置4主要用于激励产生Y+、Y-向的加速度输入，位置5、位置6主要用于激励产生Z+、Z-向的加速度输入。

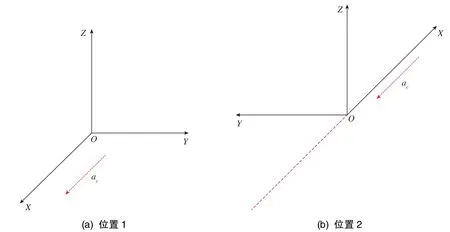
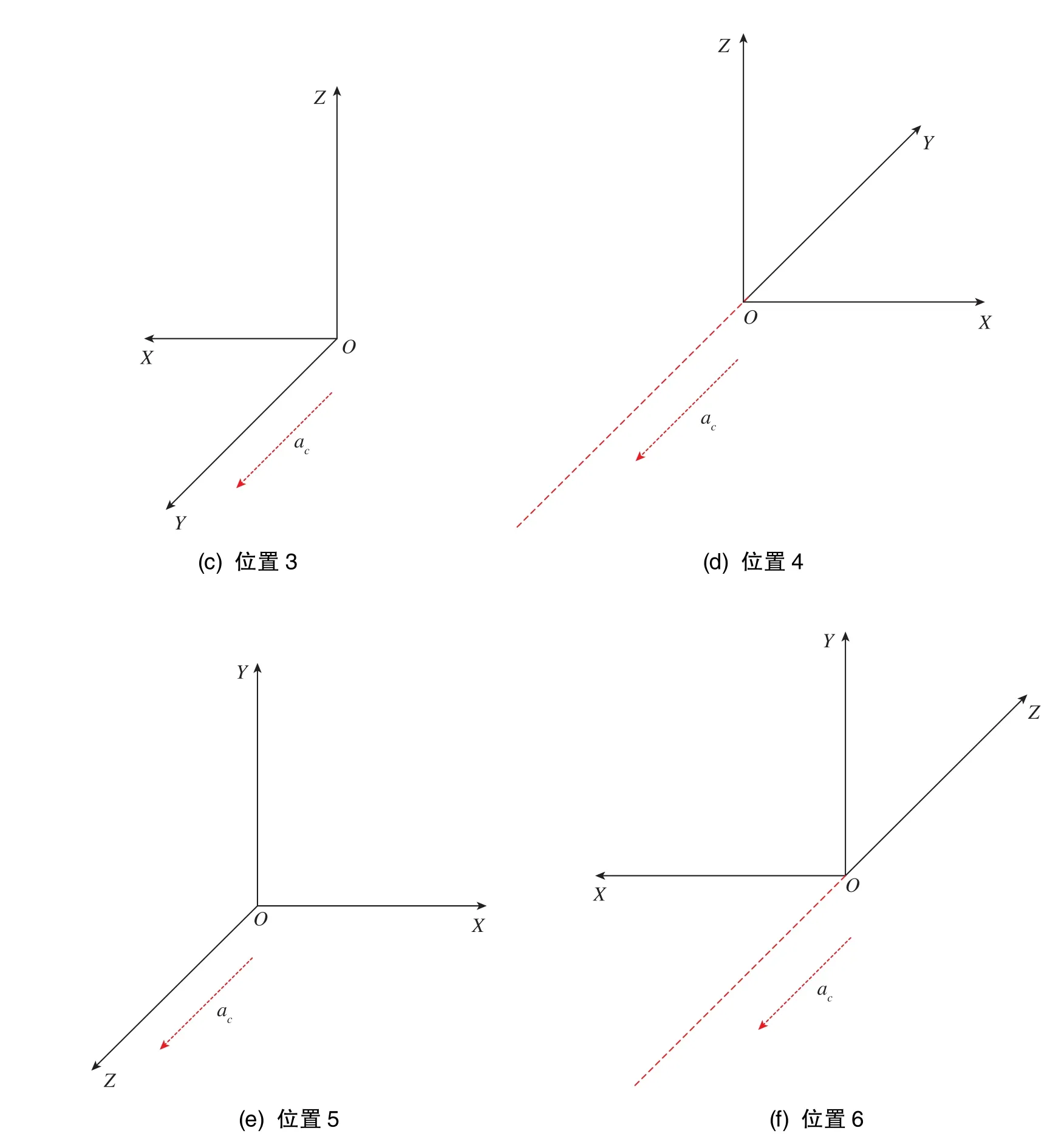
图2 MEMS IMU的安装位置示意图Fig.2 Schematic diagram of MEMS IMU installation position

2.2 试验的设计

如图3所示，MEMS IMU的加速度计建模试验包括静态测试试验和动态测试试验。静态测试试验主要用于确定零速率时传感器的输出，圆周方向多个对称位置的输出取平均值，可以得到加速度计的零输出值。动态测试试验用于采集不同向心加速度输入下MEMS IMU的三轴输出。根据MEMS IMU误差模型参数的个数和所需的测试激励设计离心机试验和数据采集的时间：

1）MEMS IMU 按照图2（a）的位置安装完成后，上电预热10min。

2）产品输出稳定后，取离心机圆周四个位置0°、 90°、 180°、 270°分别进行 3min 测试，以确定加速度计的零速率静态输出，四个位置的输出均值再取平均，得到MEMS IMU加速度计的零输出值。

3）设置离心机的转速，使得MEMS IMU的径向输出接近1g，利用式（1）通过反算法得到系统的等效半径，利用式（2）得到水平失准角，通过得到的等效半径计算离心机向心加速度为2g、4g、6g、…、20g的旋转速率。

4）依次设置离心机的旋转速率，使得离心机在MEMS IMU径向敏感轴上产生的向心加速度分别为2g、4g、6g、…、20g，每个速率点采集离心机旋转稳定后5min的MEMS IMU三轴加速度计的输出值。

5）依次调整 MEMS IMU的安装位置，如图 2（b）～图 2（f），重复步骤 1～步骤 4，获得不同安装位置下的MEMS IMU三轴加速度计的输出值。

通过步骤1～步骤5，可以得到一组 MEMS IMU三轴加速度计的离心机数据。为了进行建模验证，重复进行步骤1～步骤5，得到多组离心机试验数据，用于模型的有效性验证。

图3 离心机试验装置图示Fig.3 Diagram of centrifuge experiment apparatus

3 高g条件下的MEMS IMU加速度计误差建模

3.1 加速度计的误差模型

MEMS IMU加速度计通过检测梳齿在工作条件下的电容大小变化实现加速度的测量，工作在闭环状态下的加速度计通过静电力实现与惯性力的平衡。当静电力与惯性力中心不重合时，检测质量受力不均，将使仪表的检测输出表现出明显的非线性，尤其在大加速度条件下，非线性会更为突出［8］。当加速度计受到垂直于敏感轴方向的作用力时，梳齿电容对的有效面积也会发生变化，因此产生输出误差。为了保证模型的完备性，首先建立MEMS IMU加速度计的全参数模型，在此基础上通过数据验证和显著性分析进行模型的优化。基于前期的试验分析，MEMS IMU加速度计的误差模型仅仅跟一次项、二次项和交叉耦合项有关，加速度计的误差模型如下

3.2 试验建模数据的处理

利用离心机试验获得不同加速度输入下的加速度计数据，通过去除零输出项、扣除科氏加速度、补偿安装误差等，得到加速度计的测量输出，输出减去输入，得到加速度计的输出误差。具体的计算步骤如下：

1）利用离心机运转前和运转后的四位置数据求取零速率数据，即零输出项。

2）利用近似1g输入条件下的离心机转速求得被测产品的等效旋转半径（由于±1g产品的安装位置会发生变化，因此需要分别计算）。

3）利用离心机各加速度条件下的转速并叠加科氏加速度求得施加在被测产品在离心机径向的实际输入，垂直于径向输入的水平输入为0g，与离心机台面垂直的输入为±1g。

4）提取被测产品在±2g、 ±4g、 ±6g、 ±8g、±10g、 ±12g、 ±14g、 ±16g、 ±18g、 ±20g的三轴加速度测量输出，利用式（2）补偿水平失准角引入的误差，得到修正后的加速度计输出值。

5）被测产品的测量输出减去被测产品的实际输入得到加速度计的输出误差。

6）根据模型和加速度计的输入、输出列写方程组，基于最小二乘法，可以求得模型的系数。

7）对求解的误差模型进行模型显著性分析和模型参数显著性分析，检测模型的可信度以及模型参数的可信度。当模型的显著性检验值小于理论值时，调整模型，重新进行步骤6；当模型的检验值大于理论值时，进行模型参数的显著性分析，如果其中一些参数的检验值小于设计值，则去除不显著项，重复进行步骤6的求解，直至模型的参数检验值均大于设计值。

3.3 模型的显著性分析和模型参数的显著性分析

模型方程一般是由多个误差项组成，如式（5）所示。为了提高模型的可信度，需要对模型方程的显著性进行判别［9⁃11］，一般用单个自由度的回归平方和与单个自由度的回归误差平方和之比作为判别模型方程显著性的依据。这一比值符合概率统计的F分布规律，可以用F统计量来检验。根据试验中取得的数据，可以计算出F检验值。y是关于x1，x2，…，xm的多变量函数，通过模型辨识求得模型的各参数系数。假设y服从F分布，则模型的F分布计算值为

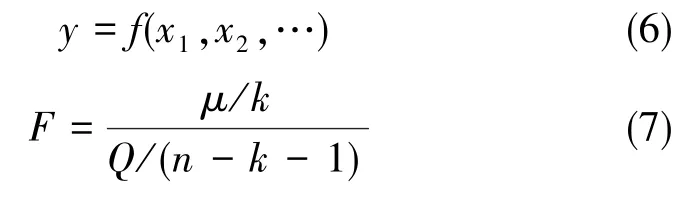
F值为y的系统误差与y的随机误差影响之比，F值越大，模型方程越显著［12］。如果F值接近1，说明系统误差和随机误差接近，模型方程没有什么实际意义。式（7）中，为回归平方和，为误差平方和，yi为实际的测量值。R2值是指复相关系数μ/S，S＝μ+Q。R2越接近1，说明模型越接近理想情形。

模型方程每一个误差项对仪表输出的影响并不相同，有些项对输出的影响很大，而有些项可以忽略，因此需要根据随机误差比较来判别模型方程中各误差项是否显著。对模型方程各系数的标准差可以用t统计量来检验其显著性，t统计值的计算表达式如下

式（8）中，ki为模型的第i个系数，σi为模型系数的协方差。测试中，取数据总个数为n，设显著水平为a，查t分布表可得t（n-k-1）值，如果计算的t值大于理论值，则认为该项系数在显著水平a时是显著的。根据经验，我们取显著性水平a＝0.05。

当模型显著性F检验值小于理论值时，需要对模型进行优化调整，重新进行分析，直至模型的显著性大于理论值。当模型的显著性满足要求时，进行模型参数的显著性分析。通过比较模型参数的t统计值与理论值（查表获得），去除不显著的模型项，重新计算模型参数值，直至模型参数的t统计值均大于理论值。具体的模型优化步骤如下：

1）当模型的显著性小于理论值时，模型调整的方法是逐项去除参数显著性最小的项，每去掉一项，重新计算一次模型系数，直到模型显著性分析F分布值大于理论值。

2）然后进行模型参数的显著性分析，按照t统计值由小到大逐项去除t统计值小于理论值的误差项，每去除一项，重新计算一次模型系数，直到模型参数显著性t统计值均大于理论值。

3.4 建模方法的试验验证

根据2.2节离心机的试验获取MEMS IMU三轴加速度计在不同输入条件下的输出值，分别提取加速度计x、y、z的输入和输出值。通过图2所示6个位置的离心试验，得到60个向心加速度输入下的加速度计输出值。根据式（5）得到 MEMS IMU加速度计x的模型参数，如表1所示。

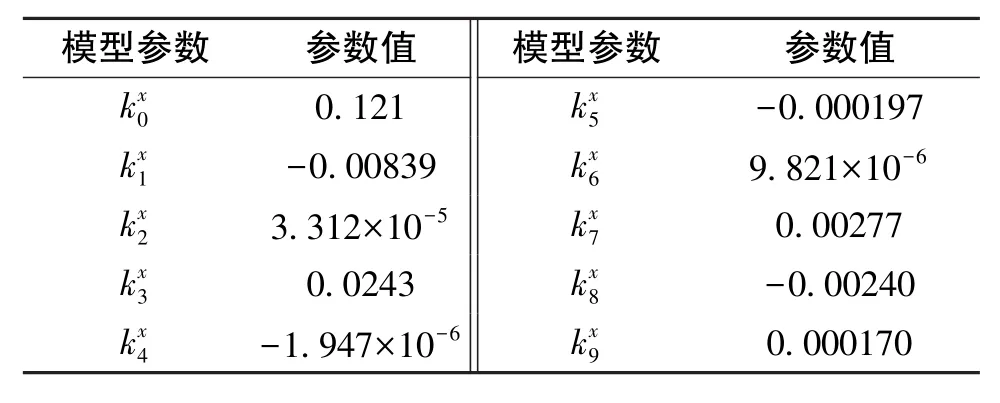
表1 加速度计x的模型系数Table 1 Model coefficients of accelerometer⁃x

模型的显著性分析F值为139.34，F（10，49）的理论值为2.08。同时，进行模型参数的显著性分析，t检验值如表2所示，t（60-10-1）的理论值为1.676。由表2可知，除前三项之外，其余项均接近或小于t分布的理论值，因此需要对模型进行优化调整。经过多轮调整，最终得到的模型包含模型参数模型的显著性F（5，54）为286.95，理论值为2.37，R2值为0.9637。此时的模型参数的显著性分析如表3所示，t（60-5-1）的理论值为1.671。通过表3可以看出，跟ax的一次项、二次项有关的误差影响比较显著，垂直于加速度计x敏感轴跟ay的一次项、二次项有关的误差影响次之，而且存在常数项误差。最后，得到的模型参数如表4所示。

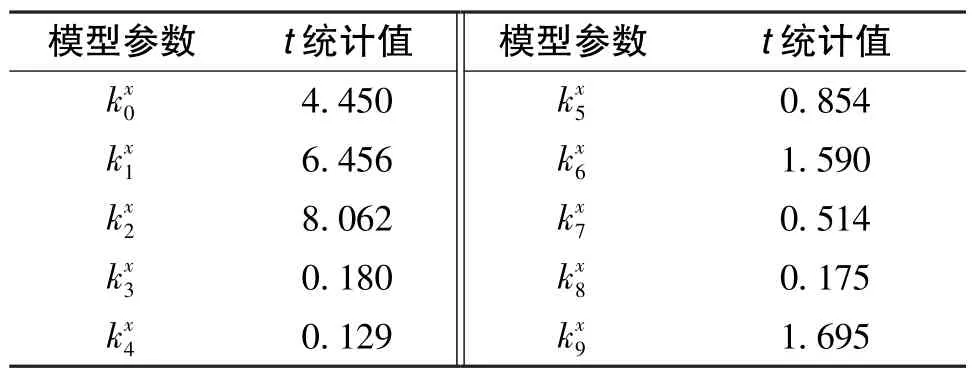
表2 模型参数的显著性分析（t统计量）Table 2 Significance analysis of model coefficients（t⁃statistic）

表3 调整后的模型参数的显著性分析（t统计量）Table 3 Significance analysis of model coefficients after adjustment（t⁃statistic）

表4 调整后的加速度计x的模型参数Table 4 Model coefficients of accelerometer⁃x after adjustment

基于建模得到的模型，对重复进行离心机试验得到的数据进行模型验证，结果如图4所示。图4（a）给出了MEMS IMU加速度计x在图2的6个位置向心加速度输入为±2g、±4g、±6g、±8g、±10g、 ±12g、 ±14g、 ±16g、 ±18g、 ±20g时的输出并取均值，共得到60个数据点。

由图 4（b）可知，当 MEMS IMU的X轴有-20g～-2g输入时，加速度计x的输出产生负相关的误差；当MEMS IMU的Y轴、Z轴有2g～20g输入时，加速度计x的输出产生一定比例的正相关误差。通过误差建模补偿，可以有效抑制输出误差。加速度计x补偿前的误差均方根值为0.6243m/s2，补偿后的误差均方根值为0.1074m/s2，误差降幅为82.8%。

图4 加速度计x的误差补偿Fig.4 Error compensation of accelerometer⁃x

对加速度计y和加速度计z进行误差建模、模型优化后，得到其模型系数和模型参数显著性统计值，如表5、表6所示。F检验值均大于理论值，说明模型是显著的、可信的。R2越接近于1，说明建立的模型越接近理想模型。加速度计y的误差模型R2值大于加速度计z的R2，更接近于1，因此加速度计y的误差更接近理想模型。由表6可知，加速度计的模型参数均大于理论值t（55）＝1.671。

表5 加速度计y和加速度计z的模型显著性分析Table 5 Model significance analysis of accelerometer⁃y and accelerometer⁃z

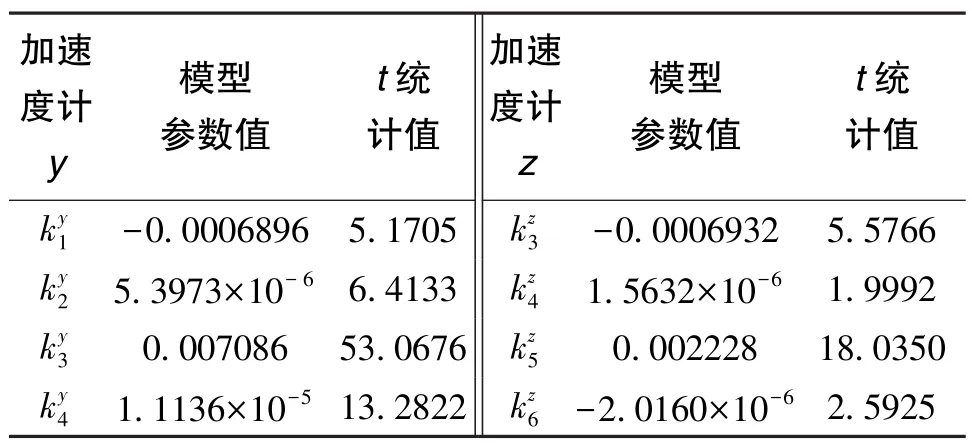
表6 加速度计y和加速度计z的模型参数显著性分析Table 6 Model coefficients significance analysis of accelerometer⁃y and accelerometer⁃z

同样，对重复进行离心机试验得到的数据进行模型验证，结果如图5、图6所示。

图5 加速度计y的误差补偿Fig.5 Error compensation of accelerometer⁃y

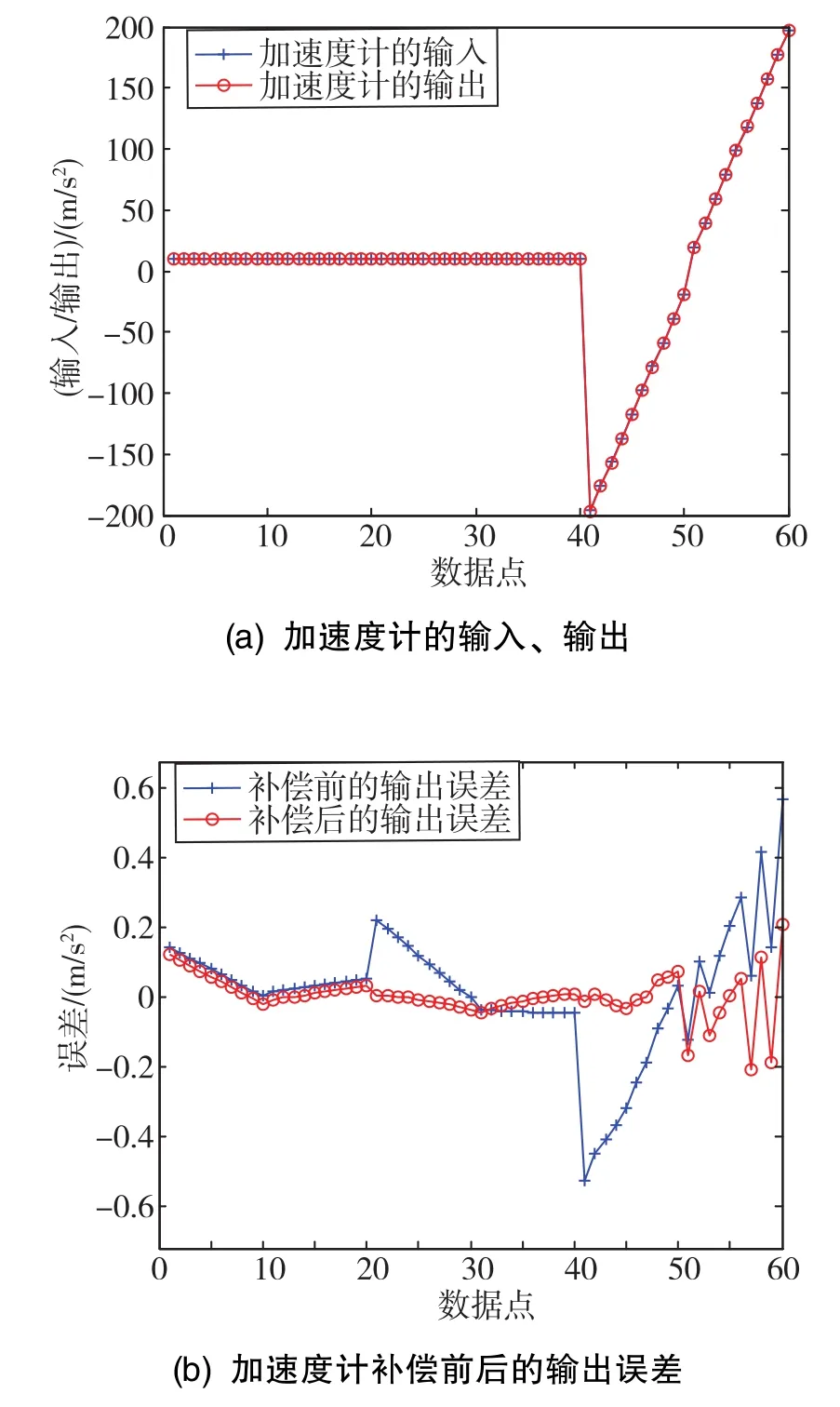
图6 加速度计z的误差补偿Fig.6 Error compensation of accelerometer⁃z

由图5可知，在加速度计y输入为-20g～20g时，加速度计的输出误差与输入呈现一定的正相关关系；在MEMS IMU的X轴输入从-20g～-2g变化时，加速度计y有负相关的误差产生。通过误差建模，输出误差的均方根值由0.5242m/s2降为0.0709m/s2，降幅达到86.47%。由图6可知，在加速度计z输入从-20g～20g变化时，输出误差呈现振荡递增变化；在MEMS IMU的X轴、Y轴输入从-20g～-2g变化时，加速度计z均有负相关的误差产生。经过误差补偿后，输出误差在不同程度上得到了有效抑制，输出误差的均方根值由0.1803m/s2降为0.0620m/s2，降幅达到65.61%。

由图4～图6可知，在敏感轴存在大加速度输入时，产生的误差也比较明显，经过补偿后的误差峰值得到大幅度削减。MEMS IMU加速度计x、y、z的误差补偿前后的最大值如表7所示（表中的统计值先取误差的绝对值，然后取其中的最大值）。由表7可知，误差补偿后，加速度计x、y、z的误差最大值分别降为原来的15.24%、13.44%、36.75%。

表7 补偿前后加速度计的误差最大值Table 7 Maximum error of accelerometers before and after compensation

通过以上分析可知，MEMS IMU三轴加速度计的输出误差不仅与敏感轴的输入有关，与垂直于敏感轴的输入也有一定的相关性。其原因在于，垂直于敏感轴的输入会导致梳齿电容对的基板有效面积或距离变化，导致检测输出的变化。

4 结论

随着小型化制导弹药精确打击、编队飞行、协同作业的需求发展，作为核心导航工作部件的MEMS IMU亟待提升其在高速机动工作环境下的精度水平。因此，开展MEMS IMU加速度计在高加速度条件下的误差建模与补偿技术研究具有重要的意义。本文给出了一种高g条件下的MEMS IMU三轴加速度计误差建模与补偿方法，分析了单轴盘式离心机试验引入的误差源及其补偿修正方法，设计了三轴加速度计的建模试验流程，基于最小二乘法完成了模型参数辨识，通过显著性分析实现了模型优化。由模型分析和验证可知：1）在高g条件下，MEMS IMU加速度计的误差跟输入加速度的一次项、二次项有关；2）误差主要受敏感轴加速度输入的影响，交叉轴的加速度输入影响次之；3）基于离心机试验，可以实现高g条件下的加速度误差建模；4）通过误差补偿，可以实现加速度计误差的有效抑制。