脉冲式冷原子干涉仪敏感惯性参量物理机制的新理解

黄 晨，乐旭广，程 俊，姚辉彬，毛海岑

（华中光电技术研究所武汉光电国家研究中心，武汉 430223）

0 引言

Mach⁃Zehnder构型的冷原子干涉仪自20世纪90年代起已发展了数十年，并大量应用在大地测量、 等效性原理验证以及惯性测量等领域［1⁃6］。 一般来说，干涉是指两列波在空间中产生叠加合成从而引起强度重新分布的一种物理现象。随着激光冷却技术的快速发展和普及，人们利用诸如磁光阱、亚Doppler冷却等方法将原子冷却至百微开以及更低的温度，使得原子的波动性可以被观测到，这使得利用原子波包进行干涉实验变得可能。由于冷原子的de Broglie波长比光的波长要短很多，其理论精度远高于传统干涉仪，冷原子干涉仪在精密测量领域有着巨大的潜力，尤其是在高精度惯性导航领域。根据传统干涉仪的定义，两个波包由于在空间中的路径不同，会积累不同的相位，这会导致两个波包在重合时会根据其积累的相位差形成稳定的干涉条纹。因此，利用冷原子进行干涉时，也需要根据原子在空间中经历分束、反射、合束过程中所走过的经典路径以及激光相位的不同，来计算其产生的相位差，最终对惯性参量进行解算，这种计算方式在静态条件下十分方便。然而，当冷原子干涉仪系统在测量过程中存在运动时，由于光反冲动量不再固定，因此计算原子轨迹就变得十分复杂，难以得到解析表达式，这给冷原子干涉仪在动态下的信号解算带来了极大的不便。

本文给出了一种脉冲式冷原子干涉仪敏感惯性参量物理机制的新理解，该解释方式基于Hei⁃senberg表象下的原子⁃光子相互作用理论，利用双光子Raman跃迁机制详细描述了在静止及运动状态下冷原子团与Raman光的相互作用，并同时将外界载体的运动等效为原子与Raman光作用的等效失谐量。由于原子⁃光子的相互作用效果会随着失谐量的改变而改变，可通过该方法给出原子的输出相位。更重要的是，由于该模型仅需要考虑Raman脉冲时刻原子与光的相对运动、位置的状态，而不必考虑在自由演化期间的原子运动轨迹，因此大大简化了得到系统运动与输出相位之间关系的计算量，这使得实时得到不同运动状态下输出相位的解析表达式变得可能，该理论的提出能够大幅度提升脉冲式冷原子干涉仪在动平台中的性能，拓宽了其应用场景。

本文首先描述了原子⁃光子Raman相互作用模型，以三脉冲冷原子干涉仪为例，得到在三束脉冲作用下原子布居数的演化，并以此为依据给出了冷原子干涉仪敏感外界运动信息新的解释方式。接着，利用上述新的物理机制得到在四脉冲冷原子干涉仪中外界运动信息与系统输出相位的关系，并利用该机制给出了四脉冲冷原子干涉仪对初始速度不敏感的一种新的解释。再次，依据该机制提出了一种在敏感轴改变情况下陀螺仪输出的相应变化。最后，给出了总结与讨论。

1 三脉冲冷原子干涉仪中原子敏感惯性参量物理机制

这里，考虑一个Λ型三能级原子，其具有两个基态以及一个激发态其本征频率分别为ωa、ωb和ωi。 使用一束 Raman光照射该原子，Raman光由两种频率构成，可以将两束激光表示为［7⁃8］

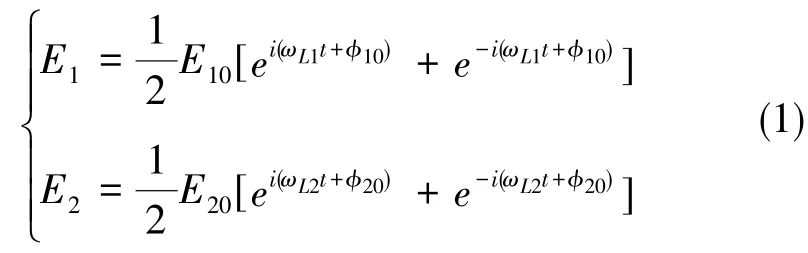
式（1）中，ωL1、ωL2为两束激光的频率，E10、E20为两束激光的电场强度，φ10、φ20为两束激光的初始相位。此时，可以写出两束激光与原子两能级作用的Rabi频率为为原子电偶极矩。据此，该光与原子相互作用的Hamiltonian量有如下形式

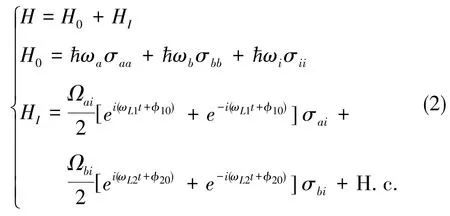
将式（2）化简为矩阵形式

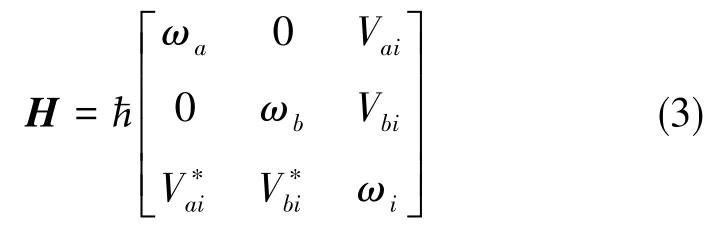
式（4）中，假设Ωai，Ωbi∈R， 则在相互作用绘景下的Schrodinger方程为

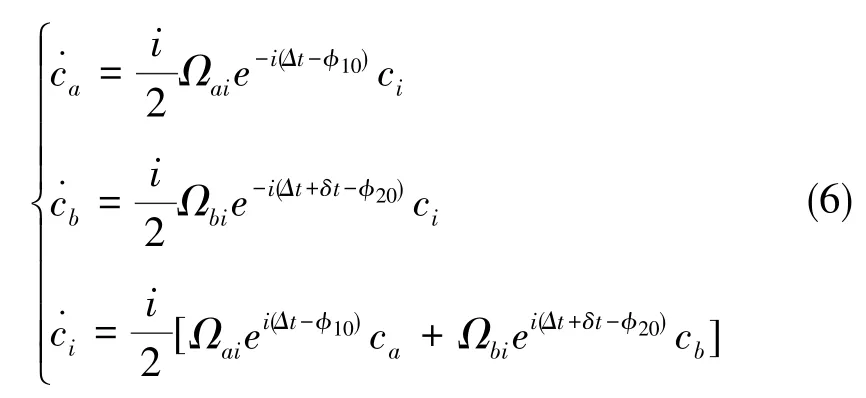
由于通常情况下有Δ≫Ω及Δ≫δ，因此这里可以对ci项直接积分，带入式（6）并使用旋波近似，可得

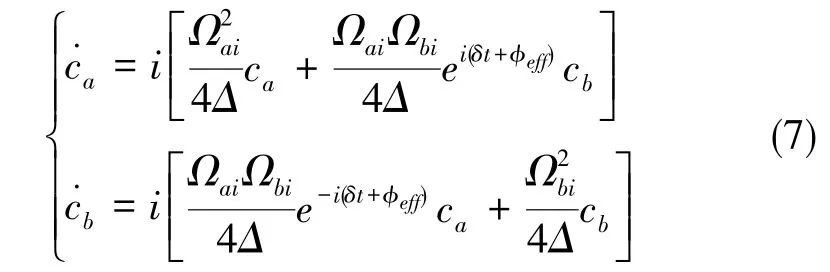
这里利用了关系Δ≈Δ+δ。 对式（7）进行同样的化简及第二次旋转变换，可得

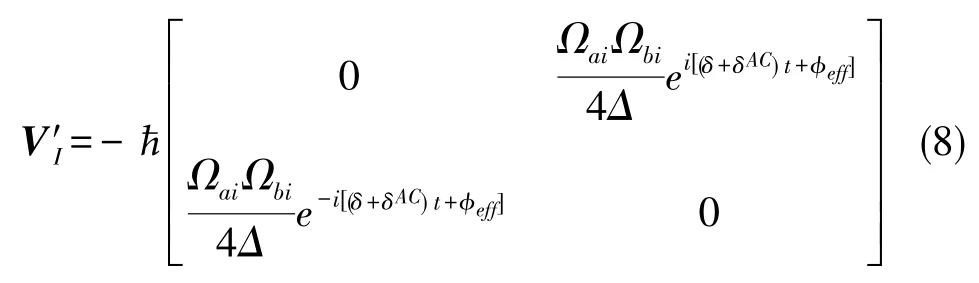
实际情况中，由于原子与Raman光的作用角度和原子运动速度的改变，原子感受到的Raman光频率不一定为ωeff。 这里的Doppler频率会由许多因素引入，如重力、转动、振动等，该Doppler失谐大小设为这里定义γ（t）为 Doppler失谐量随时间的变化率。显然，由于外界运动的不确定性，γ（t）为随时间变化的函数。为了便于表达其中的物理机制，这里考虑特殊情况，即γ（t）＝γ。 在这种情况下，可以根据前文中的定义写出原子感受到的Raman光的总失谐量为δ＝δ0+γt。根据主方程可以写出原子内态算符的Bloch方程

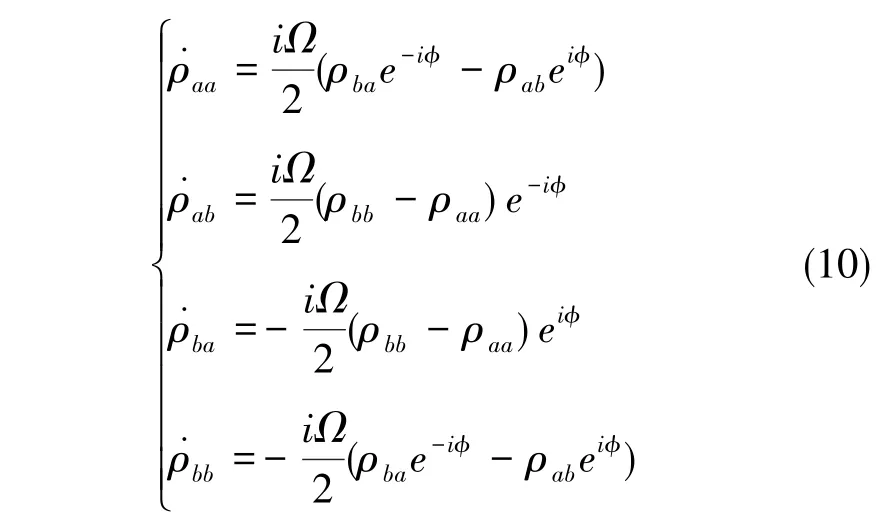
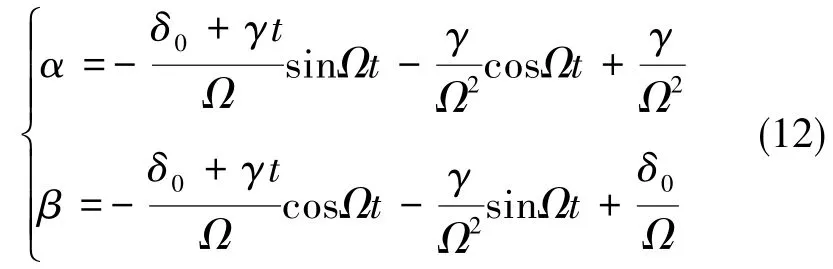
而原子在自由演化过程中的内态为

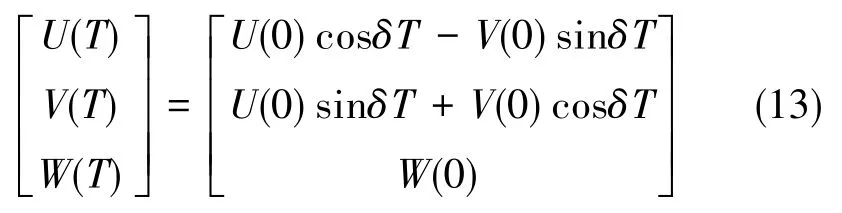
通过式（11）、 式（13），可以得到在三束 Raman光完成π/2→π→π/2过程之后原子处在态上的概率为

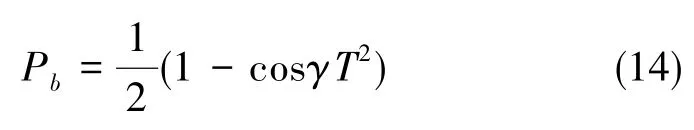
显然，通过式（14）可发现，失谐变化率γ与系统输出相位直接相关。实际上，正是由于γ的存在，才能利用这种原子干涉现象来测量对应的物理量。换言之，若某个物理量对原子失谐没有任何贡献或者为恒定值，则可以看到γ≡0时式（14）中的γT2≡0。 即使该物理量可能本身在随时间变化，但是由于它对失谐量的贡献不随时间变化，原子干涉仪并不能对这类物理量进行测量。

2 失谐变化率产生的物理机制

根据上述分析，接下来需要搞清楚各惯性参量是如何引起原子⁃光子相互作用中失谐变化率的变化。为了能够更清晰地揭示其中的物理机制，这里首先考虑原子仅在重力场中的运动，然后再研究在转动情况下的失谐变化率。

若考虑重力场的影响，原子在竖直方向上的速度表达式为v＝gt，t为原子离开磁光阱所经历的时间。因此，若Raman光与重力方向的夹角为θ，如图1所示，可以写出原子感受到的Raman光的失谐随时间的变化为

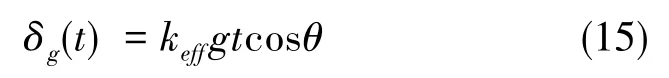
图1 在重力场作用下原子感受到Raman光的Doppler频移示意图Fig.1 Doppler frequency shift of Raman laser felt by atoms under the gravity field

如图2所示，若考虑转动的影响，由于原子从抛射出去之后为自由飞行状态，转动仅仅影响Raman光的角度。或者等效地来讲，假设Raman光静止，原子与Raman光的相对速度就是由于转动引起的。这里等效地认为第一束Raman光与原子相互作用的位置为圆心，即在该点原子与Raman光保持相对静止，且Raman光与转动方向垂直。由于原子经过三束Raman光的时间非常短，因此可以认为在小角度转动下原子由于转动产生的相对线速度Δv＝ΩLi就是沿着Raman光方向的（这里Li为第i束Raman光与第一束Raman光的距离）。那么，此时由于转动产生的线速度所引起的Doppler频移随时间变化的函数可以表示为

式（16）中，r为原子位置矢量。

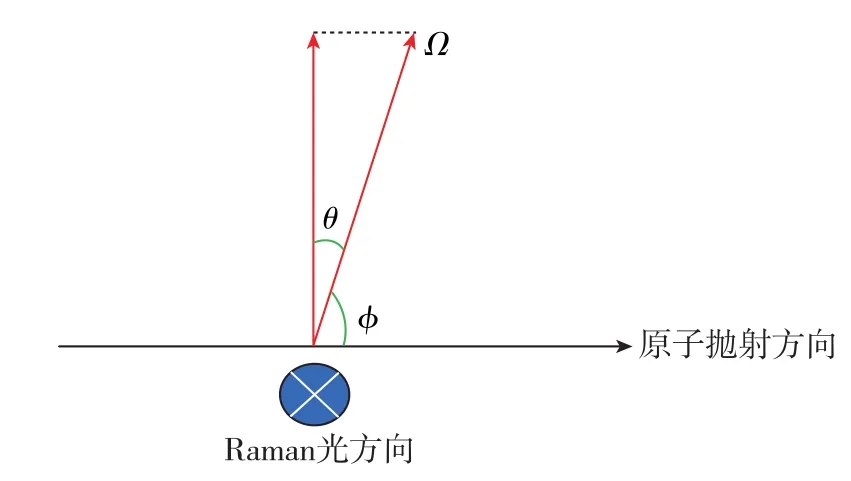
图2 存在转动情况下原子感受到Raman光的Doppler频移示意图Fig.2 Doppler frequency shift of Raman laser felt by atoms in rotation situation

若原子速度与转动不垂直，假定现转动方向与垂直转动方向的夹角为θ，由图2可知，可以造成Doppler频移的转动其大小为Ωcosθ。 由于Raman光与原子速度垂直，则cosθ＝sinφ，那么可以将式（16）改写为

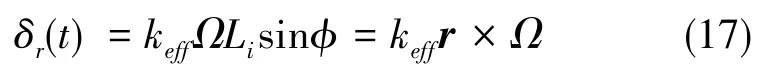
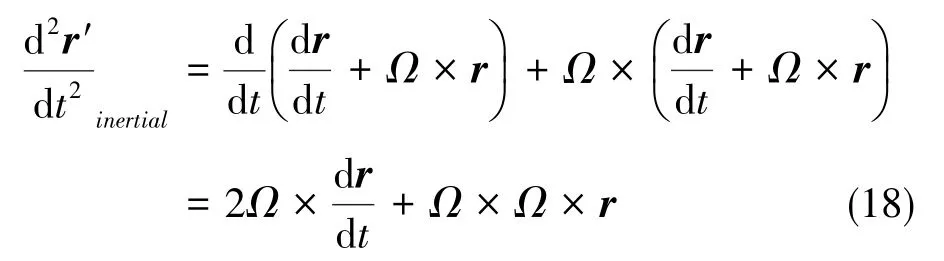
显然，式（18）中的第二项与Raman光方向垂直，不会产生Doppler频移，并假设转速Ω为常数，故此时γ＝2Ω×v。 通过观察式（18）还可以发现，事实上γ是由两项组成的，只不过在这种情况下两项的大小相等，因此合并成为一项。

由这种方式虽然能够推导出γ的表达式，但只是从数学上给出了一个表达式，并不能直接对应于物理现象与物理机制。那么，接下来对转动引起的Doppler频移给出一个更清晰的物理上的阐述。忽略地球自转，从实验室这个固定参考系来观察整个系统。不失一般性，假设整个系统以第一束Raman光与原子相互作用的那个点进行旋转，并且以相遇的时刻为零时刻开始以角速度Ω进行旋转。那么，可以观察到原子是沿x方向水平向右移动，当原子团飞行至第二束Raman光的位置时，旋转对π脉冲有两方面的作用：

1）如图3所示，Raman光与原子的作用角度变化了ΩT（该项在原子速度为零时消失），此时可得到在Raman光方向上原子的分速度为vsinΩT，即其Doppler频移为keffvsinΩT。由于ΩT≪1，有频移近似为keffvΩT，可以认为该项对应于式（18）中的一项，即此时为定值，失谐产生于转速Ω对时间的积分，则实际该项引起的失谐可以改写为

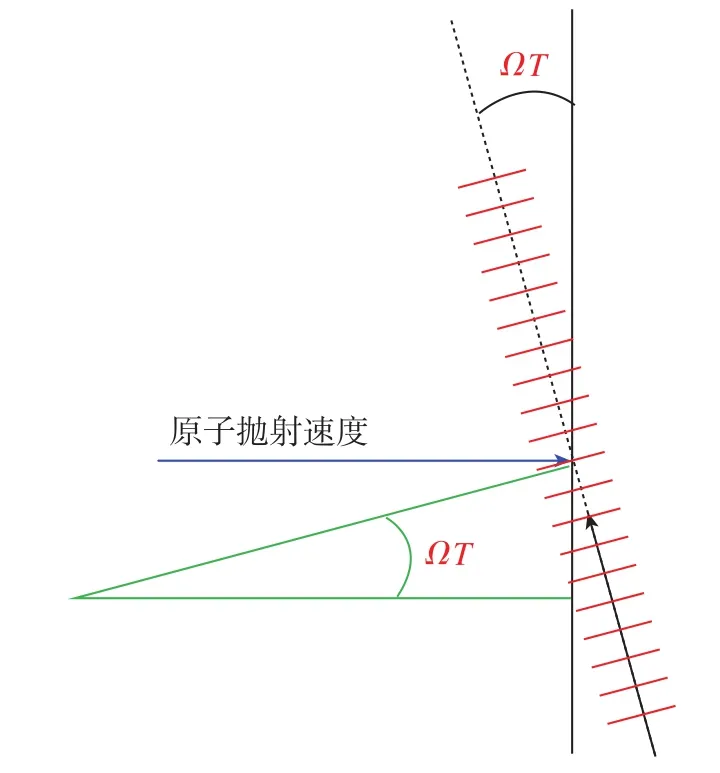
图3 三脉冲构型干涉仪Raman光与原子作用角度变化示意图Fig.3 Schematic diagram of interaction angle between Raman laser and atom ensemble in three⁃pulse atomic interferometer

2）如图4所示，原子由于转动产生的位移可等效为在Raman光方向的线速度引起Doppler失谐。当外界存在转动时，原子与Raman光作用的位置相比没有转动时会改变，这是由于非轴心处Raman光光源在移动，而原子在惯性系中自由飞行。在三脉冲陀螺中可以等效为原子在Raman光方向由于转动会产生线速度，其大小为ΩT，这里L＝vT为两束Raman光之间的距离。由于该速度的方向在T极小的时候可以近似认为是切向，即速度方向与Raman光方向一致，则该相对速度所引起的失谐可以表示为keffΩL， 可以认为该项对应于一项，即此时失谐产生于转速与位置的乘积

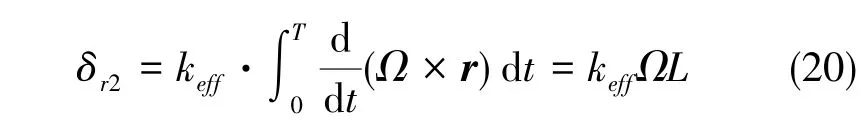
综合上面两部分，可以得到总的失谐为

至此，给出了一种脉冲式冷原子干涉仪敏感惯性参量物理机制的新理解，该解释方式给出了更清晰的物理图像。该解释首次清晰地分离了由转动引起Doppler频移的两个组成部分，其中一种依赖于原子抛射速度，而另一种与抛射速度无关。虽然在三脉冲构型的原子干涉仪中这两部分相等，但该现象仅仅是巧合，在四脉冲构型的干涉仪中，这两项就有了完全不同的贡献，该部分内容将在下一章中介绍。更重要的是，该机制的解释更便于给出动态情形下的输出相位表达式。

3 四脉冲冷原子干涉仪中原子敏感惯性参量物理机制与相关特性

这里考虑四脉冲冷原子干涉仪，参照本文的推导过程，四脉冲冷原子干涉仪的输出相位与失谐变化量的关系为

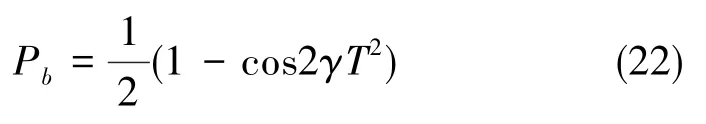
那么，按照新的物理机制来计算在四脉冲情形中具体的表达式形式。显然，原子干涉仪测量的是测量过程中的平均转速，因此这里考虑第一束Raman光与最后一束Raman光的变化，并将其取平均。这里假定原子初始抛射速度为v0，自由三段演化时间长度分别为T、2T和T，重力加速度恒为g。

1）如图5所示，Raman光与原子的作用角度变化了4ΩT，则由于该项产生的Doppler频移为

显然，由图5可知，该项使得原子感受到的Raman光频率增加。

图5 四脉冲构型干涉仪Raman光与原子作用角度变化示意图Fig.5 Schematic diagram of interaction angle between Raman laser and atom ensemble in four⁃pulse atomic interferometer

2）如图6所示，原子由于转动产生的位移可等效为其在Raman光方向的线速度的变化，其大小为

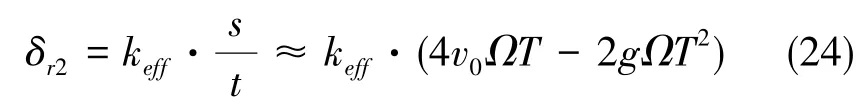
同样由图6可知，由于等效位移方向为远离光源，因此该项会使原子感受到的Raman光频率变低。

图6 四脉冲构型干涉仪原子由于转动产生的相对位移示意图Fig.6 Relative displacement of atom ensemble due to uniform rotation in four⁃pulse atomic interferometer

综上所述，在四脉冲构型的冷原子干涉仪中，由于转动产生的失谐变化总量为

由式（25）可知，虽然在四脉冲构型中引起失谐量变化的两项都与初始抛射速度v0相关，但最终相互抵消，使得四脉冲构型最终输出相位与初始抛射速度的大小无关。

4 动态情况下三脉冲冷原子干涉仪输出响应

本节中，考虑在动态情形时存在三轴转动情况下三脉冲冷原子干涉仪的输出响应，首先建立实验室坐标系：以原子抛射方向为x轴，以初始Raman光方向的反方向为y轴，以为z轴。假设有三轴转动Ω，可将其分解为三个方向的转动并分别进行讨论，即Ω＝Ωx+Ωy+Ωz。 显然，由于采用的是实验室坐标系，而原子在抛出之后是在惯性空间中自由飞行，即可以将系统的转动等价地理解为Raman光方向的转动。这里为了讨论的简便，假定转动均为匀速转动，并不考虑重力加速度。

下面利用前文给出的物理机制对该情形下干涉仪的响应进行分析。

（1）x轴方向上的转动Ωx

如图7所示，不失一般性，假设此时系统感受到的转动为Ω＝Ωx+Ωz，则根据前文的分析，在初始状态下进行Ωx的旋转并不会影响初始状态下原子的失谐。因此，不妨假定在初始状态后一瞬间，系统沿x轴旋转了ΩxT角度，接下来，系统只感受到Ωz的旋转，并持续了T时间。这种情况下，原子等效于在Raman光方向为y′轴时进行了的旋转，即图7中的显然有

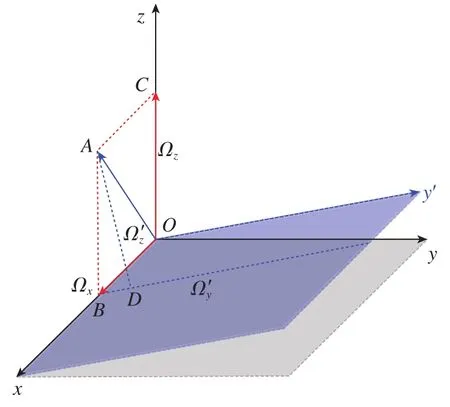
图7 沿x轴旋转时的分解示意图Fig.7 Exploded diagram of rotation along x⁃axis

可以简单理解为系统感受到的是原转动的投影。由于待测转动的转轴不变，则式（26）中转动Ω的方向为z轴方向。这里以第一束Raman光为基准，令第二束以及第三束Raman光在yoz平面内旋转的角度分别为θ1和θ2， 则可以求得原子在第一束Raman光与第二束Raman光之间失谐的变化率，相当于原失谐变化率的一个投影，即

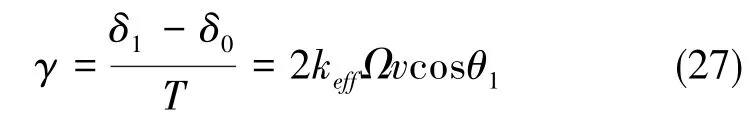
这里，假定通过事先调节使得第一束Raman光与原子的失谐为零，即δ0＝0。 通过类似的计算，可以得到原子在第二束Raman光与第三束Ra⁃man光之间失谐的变化率为

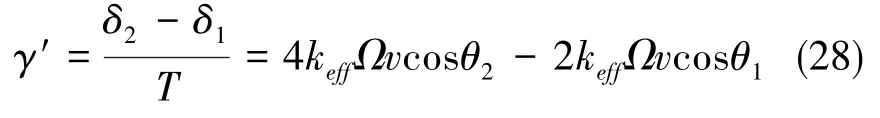
结合式（27）、 式（28），如图8所示，可以得到原子干涉仪的最终输出相位为

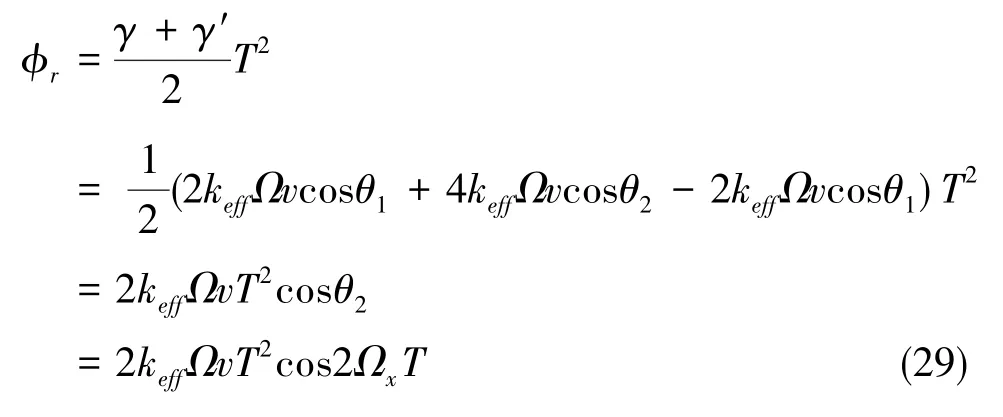
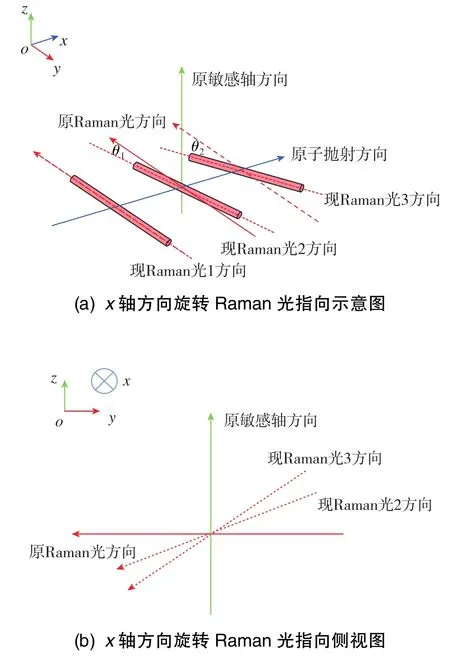
图8 三脉冲构型干涉仪中Raman光沿x轴转动示意图Fig.8 Diagram of Raman laser rotation along x⁃axis in three⁃pulse atomic interferometer

（2）y轴方向上的转动Ωy

如图9所示，显然沿y轴转动不会影响keff的方向，即在Ωy的转动下keff×v的大小和方向均不会改变。因此，Ω·（keff×v）保持不变，这一项不会引起输出值的变化。但需要注意的是，Ωy转动会引起原子与Raman光的相对位置发生改变，通常在Raman光光斑足够大的情况下该项可以忽略。

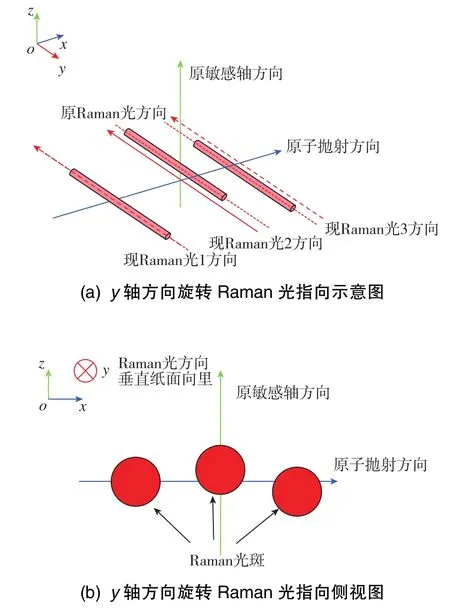
图9 三脉冲构型干涉仪中Raman光沿y轴转动示意图Fig.9 Diagram of Raman laser rotation along y⁃axis in three⁃pulse atomic interferometer

（3）z轴方向上的转动Ωz

如图10所示，显然，沿原敏感轴的转动分量可以直接等效地加入待测转速中。

图10 三脉冲构型干涉仪中Raman光沿z轴转动示意图Fig.10 Diagram of Raman laser rotation along z⁃axis in three⁃pulse atomic interferometer

综合以上三种情形，在实际情况下外界载体的三轴转动Ω会引起的输出量偏差为

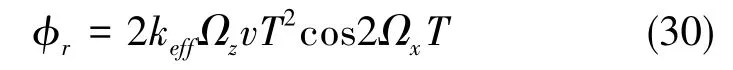
至此，新的物理机制揭示了在三轴转动下原子干涉仪的相位输出，该方式比原有计算原子空间轨迹的方式可以更直接、更清晰地给出干涉仪的输出相位表达式，更有利于将原子干涉仪运用在动态场景当中。

5 结论

综上所述，本文首次给出了在转动过程中原子与光相互作用失谐的两种不同变化来源是导致原子干涉仪能够敏感到惯性参量的物理本质。该新机制的提出大大简化了原有利用原子轨迹的路径积分来计算干涉仪输出相位的方法，并更进一步给出了脉冲式原子干涉仪在三轴转动情形下的输出表达式。这种对原子干涉仪输出响应的新理解显著提升了该类系统在复杂情形下的解算可行性，并为未来可能的动平台应用打下了坚实的基础。