借助合同变换巧解初等几何问题

黄卫华

（文山学院 人工智能学院，云南 文山 663099）

合同变换在现实生活中应用广泛，是物体运动变化中的一种简单形式，也为生活中的图案设计打下基础。合同变换的应用在初等几何变换中有着举足轻重的地位。利用合同变换解决初等几何问题是一种必不可少且行之有效的方法。一些所给条件较少，且比较分散的初等几何问题的证明和求解往往比较困难，合理运用合同变换可以把分散的条件集中起来，观察变换前后的图形，发现原图中隐藏的关系，能为顺利解题创造条件，从而起到事半功倍的效果。

郑群在文献[1]中论述了合同变换的性质及解题方法；叶述金[2]阐述了合同变换思想在解平面几何题中的优势；中学几何教学离不开初等几何变换[3-5]，常常借助合同变换证明、求解几何问题；刘清泉和董小平等学者详列了三种合同变换在几何证题中的运用[6-7]；几何证明大多需要添加辅助线，利用辅助线可以得到清晰的思路[8]；平移和旋转变换的证明题较多且难，把握解题思路和有效方法有利于问题的解决[9-11]；随着新课标改革，合同变换的地位变得愈发明显，在中学教学中[12-13]实施新的教学方法，离不开变换思想的研究[14-15]；研究依托于大量的习题，并从中发现一般规律[16-17]。这些学者从合同变换的性质出发，分析总结了合同变换在初等几何问题中的解题技巧和方法运用。

合同变换有很多种，本文主要讨论利用平移、旋转、轴反射（轴对称）这三种合同变换求解或证明初等几何问题。

1 平移变换

1.1 定义和性质

定义：将图形F上的所有点都按一定的方向l→（平移方向）移动一个相同的距离|l→|（平移距离），移动后的点构成图形F′，图形F到图形F′的变换T称为平移变换，简称平移。 记为

性质：（1）对应点的连线平行且等于平移向量；（2）对应线段平行且相等；（3）对应角相等，且角的两边同向平行；（4）平移变换不改变图形的合同、结合、顺序性。

1.2 例题分析

例1 如图1，在矩形ABCD内取点M，证明：存在一个四边形，它的对角线互相垂直且长度等于AB和BC，而边长分别等于AM、BM、CM和DM。

图 1

分析：这是一个存在性问题，关键是设法构造一个符合条件的四边形。而平移不改变线段的长度且保持方向，考虑用平移将6条线段集中起来。

证 明：，则因为AB⊥BC，所以故四边形BMCM′即为所求。

例2如图2，在“风车三角形”中，AA′=BB′=CC′=2。 求证：

图 2

分析：题中三条已知线段相交于一点O，通过平移变换，可以集中在同一个三角形中，从而使得分散的条件集中，题目迎刃而解。

证明：如图3，将由知R，Q，P三点共线。又因为OP=C′C=2，OR=B′B=2，RP=A′A=2，所以ΔRPO是边长为2的正三角形。即

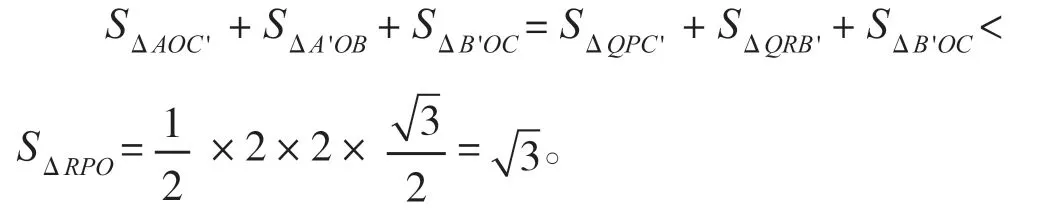
图 3

2 旋转变换

2.1 定义和性质

定义1：将图形F上的所有点都绕平面上的一个定点O（旋转中心）旋转一个相同的角度θ（旋转角），旋转后的点构成图形F′，图形F到图形F′的变换R称为旋转变换，简称旋转。 记为F′。 逆时针旋转，θ取正值，顺时针旋转，θ取负值。

性质1：（1）图形F与F′是全等图形；（2）结合性、顺序性是旋转变换下的不变性；（3）对应线段相等，且夹角为θ（有向角），对应角相等；（4）旋转中心O与每一对对应点的连线段相等，且夹角为θ；（5）旋转由中心与一对对应点完全确定。

定义2：将图形F上的所有点都变为关于平面上的一个定点O（对称中心）的对称点，变换后的点构成图形F′，图形F到图形F′的变换称为中心对称变换，简称中心对称。

性质2：（1）对应点的连线过对称中心O，且被对称中心O平分；（2）对应线段相等，且反向平行或共线；（3）对应角相等，且角的对应边反向平行。

2.2 例题分析

例3如图4，P是正三角形ABC内的一点，∠APB，∠BPC，∠CPA的大小之比是3∶4∶5。求以PA，PB，PC为边的三角形的三个内角的大小(从小到大)之比。

图 4

分析：条件过于分散，设法集中起来以便发现联系，可做旋转变换。

故以PA，PB，PC为边的三角形的三个内角∠PP′C∶∠P′PC∶∠PCP′= 30°∶60°∶90°= 1∶2∶3。

小结：借助于60°的旋转变换，将Y型线段组转化为三角形的三条边，通过解三角形解决该类几何问题。

例4已知抛物线以抛物线的顶点为对称中心,做中心对称变换,求变换后的函数解析式。

分析：设出待求函数上的任意一点的坐标,通过坐标对称变换求出满足已知函数的坐标,代入求解即可。

解：设变换后函数图像上任一点M(x,y)，M关于抛物线顶点0(-4, -3)的对称点坐标为M′(x′,y′)，则由中点坐标公式得代入已知抛物线方程，并化简得变换后的函数解析式为

小结：把一个图形变为关于定点对称的图形的变换即为中心对称变换,利用中点坐标公式将变换前后的对应点联系起来，是解决该类问题的关键。

3 轴反射变换

3.1 定义和性质

定义：将图形F上的所有点都变为关于平面上的一条直线l（对称轴）的对称点，变换后的点构成图形F′，图形F到图形F′的变换S称为轴反射变换，简称轴反射（或轴对称），记为

性质4：（1）对称变换下图形F1与F2镜象合同，即图形全等，但转向相反；（2）不在对称轴上的一对对应点的连线互相平行且被对称轴垂直平分；（3）与对称轴平行的直线的象仍是与对称轴平行的直线；（4）对应线段相等，且延长后交于对称轴l的同一点，两线形成的角被对称轴l平分，对应角相等；轴反射问题一般以三角形的边或对称轴为轴作反射变换。

3.2 例题分析

例5如图5，在ΔABC中，AB=AC，∠BAC=80°，P是三角形内一点，使∠PBC= 10°，∠PCB=20°，求∠PAB的度数。

图 5

分析：借助轴反射变换，构造全等三角形，利用特殊三角形又得到另一组全等三角形，再利用四点共圆，找出角的等量关系，进而解决问题。

解：将，连结PP′，BP′。由于ΔCPP′是正三角形（PC=PC′，∠PCP′ = 60°），得ΔBPP′ ≅ ΔBPC（SAS），所以∠P′BC= 20°。 因为A、B、C、P′四点共圆（∠ABP′ = ∠ACP′ = 30°），所以∠PAC= ∠P′AC= ∠P′BC= 20°。 即∠PAB= 80°-20°= 60°。

例6如图6，P为∠MON内一定点，且∠MON=40°，A、B分别是OM和ON上的两个动点，当ΔABP的周长最小时，求∠APB。

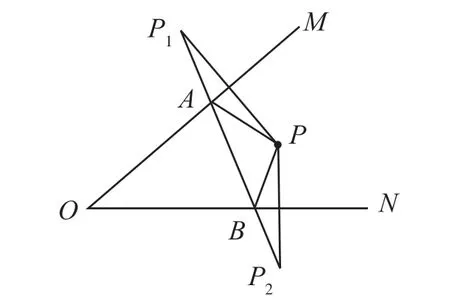
图 6

分析：将ΔABP的周长转化成两定点间线段的长度。作P点关于OM和ON的对称点P1和P2，线段P1P2的长度即为ΔABP的最短周长。

解：设P1、P2分别为P关于OM和ON的对称点，直线P1P2交OM和ON于A、B两点，则ΔABP的周长为最小。在ΔABP中，显然∠BAP=2∠P1，∠ABP= 2∠P2，∠APB= 140°- ∠P1- ∠P2，在ΔABP中，∠APB=180°- ∠BAP-∠ABP= 180°- 2∠P1- 2∠P2，解得∠P1+ ∠P2= 40°，从而∠APB= 100°。

小结：当一个角变成平角时，其角平分线就变成了垂线。因此对有直角或垂直条件的问题，可考虑利用轴反射变换寻求解题策略。

4 结论

平移问题主要抓住平移的点，找出部分平移得以解决问题。平移变换在几何证题中常用在证明线段相等、平行及角的相等等问题中；用旋转变换解几何题，首先应考虑有无做旋转变换的条件，一般要有等腰三角形，旋转保持一边变到另一边；正n边形绕中心旋转时，图形不变；含有45°的正方形问题是典型的夹半角问题，其典型解法是利用90°的旋转变换。应注意伴随着每一个90°的旋转变换均有一个轴反射变换。