巧变换、妙解题、悟化归

张玲玲 戚有建

著名数学教育家波利亚曾说过：“解题过程就是不断变更题目的过程，我们必须一再变更它的形式，重新叙述它，改变观察问题的角度，使问题呈现出新的面貌，引发我们新的思考、新的联想，直到最后成功地找到一些有用的东西为止．”而变换恰恰就是变更题目的一个重要途径，高中阶段常见的变换有：平移变换、对称变换、旋转变换、伸压变换．通过变换，可以改变问题的呈现形式，凸显问题间的相互联系，揭示问题的内在本质，可以将陌生问题化归为熟悉问题、将复杂问题化归为简单问题．本文结合实例谈谈数学变换在优化解题中的巧妙应用．

一、平移变换

例1（2021年江苏联考题）已知函数y=kx+b与函数y=ex-1-e1-x的图象交于A,B,C，且则实数k=_______．

分析本题是调研考试的最后一道填空题，难度较大．不少同学选择联列方程组处理，但是由于参数较多，计算烦杂，只能放弃．由于平移不改变线段的长度和直线的斜率，此题可以将函数y=ex-1-e1-x的图象向左平移1 个单位长度，得到奇函数y=ex-e-x的图象，从而利用函数的对称性解决问题．

收纳袋

1．平移不改变线段的长度和直线的斜率．

2．函数y=ex-a-ea-x的图象具有对称性，对称中心为(a,0)．

解析通过平移，问题简单化为：

“已知函数y=kx+b′与函数y=e-xe-x的图象交于A′,B′,C′，且，则实数k=_______．”

此时奇函数y=e-xe-x关于坐标原点对称，且是递增函数，由可知直线l′经过坐标原点B′(0,0)．

设A′(x,ex-e-x),x＞0，由得

观察出x=1 满足要求，下面说明唯一性，

令f(x)=e2x+e-2x+x2(x＞0)，则f′(x)=2e2x-2e-2x+2x＞0，所以f(x)在区间(0,+∞)上递增，所以方程①仅有一根x=1，此时可求得

点评：本题的难点和关键是发现函数y=ex-1-e1-x的对称性，通过平移将函数y=ex-1-e1-x转化为奇函数y=ex-e-x；另外通过平移同时将问题进行了简化，此时容易由及单调性发现直线l′经过对称中心．由于平移仅改变图形的位置，而不改变大小和形状，这一特性给我们解决问题会带来意想不到的效果．

二、对称变换

例2（2020·山东卷）已知函数f(x)=aex-1-lnx+lna，若f(x)≥1，求实数a的取值范围．

分析本题处理方法很多，例如：1.直接研究f(x)min；2．先从必要条件入手求出参数a的初步范围，然后再研究f(x)min；3．主元法，以a为主元，研究h(a)=aex-1-lnx+lna(a＞0)．

当然，也可构建同构式，借助单调性处理；或者抓住对称性（即反函数）处理．

解析1 构建同构式，借助单调性处理.

因为a=elna，所以aex-1-lnx+lna≥1等价于elna+x-1+lna-1≥lnx．

两边加上x得elna+x-1+lna+x-1≥x+lnx=elnx+lnx．

令g(t)=et+t,则g(lna+x-1)≥g(lnx),

可证得g(t)为单调增函数，所以lna+x-1≥lnx，即lna≥lnx-x+1．

令h(x)=lnx-x+1,则h′(x)=所以h(x)在(0,1)上递增，在(1,+∞)上递减，所以h(x)max=h(1)=0，所以lna≥0，即a≥1．

收纳袋

借助原函数、反函数的对称性命题的思路：先给定一个含参函数g(x)=ex+t，然后构建不等式g(x)≥g-1(x)（即ex+t≥lnx-t），再替换参数（令lna-1=t），最后对其变形改写即得不等式aex-1-lnx+lna≥1．

解析2 借助对称变换处理.

不等式aex-1-lnx+lna≥1即aex-1+lna-1≥lnx，令lna-1=t，则a=et+1，原不等式转化为ex+t≥lnx-t．

因为函数y=ex+t与y=lnx-t的图象关于直线y=x对称，所以ex+t≥lnx-t转化为ex+t≥x．

令g(x)=ex+t-x，则g′(x)=ex+t-1，当x<-t时，g(x)递减，当x>-t时，g(x)递增，故g(x)min=g(-t)=1+t≥0，所以t≥-1，所以a≥1．

点评：解法1 从题目的结构入手，构建同构式，借助单调性处理不等式，非常简洁，但其中改写成同构式的变形过程技巧性较强，不容易想到．解法2 则是从对称性入手，将指数函数、对数函数之间的关系转化为指数函数与一次函数之间的关系，从而简化了问题．

三、旋转变换

例3（2020·福建联考题）已知动点P在函数的图象上，定点A(-4,0)，则线段AP长度的最小值是________．分析构建目标函数求最值，即研究的最小值，但是目标函数的结构复杂，需对其变形改写,此外也可以将原函数通过变换变形改写．

解法1 换元处理.

令t=x+2，则所以当且仅当t=时，g(t)min=12，故AP长度的最小值为此时

收纳袋

解法2 借助旋转变换处理.

先向右平移2 个单位长度，再向下平移2 个单位长度，将函数简化为从而得到一个等价问题：

“已知动点P在函数的图象上，定点A(-2,-2)，则线段AP长度的最小值是________．”

“已知点P是双曲线上的动点，定点则线段AP长度的最小值是________．”

此时，就转化为我们很熟悉的双曲线中的最值问题，于是有：

设P(x,y)，则当且仅当时取等号，所以AP长度的最小值为此时

点评：通过图象的平移、旋转变换，在函数与圆锥曲线间建起了一座桥梁，使得“天堑变通途”，将原本较为复杂的一个函数最值问题最终转化为较为简单的圆锥曲线中的最值问题，揭示了问题的实质．另外，方法1 中的换元实际上就是平移变换，但是我班同学并不是很轻松地想到了换元，值得反思．

四、伸压变换

例4（2014·全国卷）已知点A(0,-2)，椭圆的离心率为F是椭圆E的右焦点，直线AF的斜率为O为坐标原点．

（1）求E的方程；

（2）设过点A的动直线l与E相交于P，Q两点，当△OPQ的面积最大时，求直线l的方程．

分析第（2）中，可以构建关于面积的目标函数来研究最值，也可以通过压缩转化为圆中的最值问题来处理．

解析（1）（过程略）．

（2）解法1：构建目标函数求最值．

当l⊥x轴时不合题意，故设直线l∶y=kx-2，代入得(1+4k2)x2-16kx+12=0．

当Δ=16(4k2-3)＞0，即k2＞时，设P(x1,y1)，Q(x2,y2)，则从而

又点O到直线PQ的距离所以

解法2：借助伸压变换处理．

先将椭圆沿x轴方向压缩为原来的变成单位圆，从而转化为圆中的问题，即下面这道题：

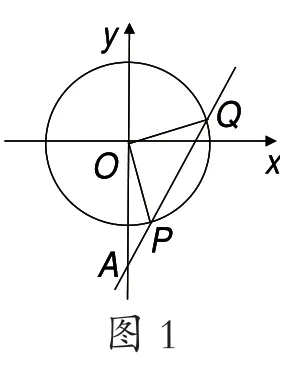
“过点A(0,-2) 的直线l与圆x2y2+=1 相交于P,Q两点，当△OPQ的面积最大时，求l的方程．”

此时非常简单，由于S△OPQ=OP×OQ×sin ∠POQ=sin ∠POQ，

故当∠POQ=90°时，

此时设直线l:y=kx-2，则由∠POQ=90°得解得

点评：方法1 是构建目标函数来处理，是通法，但是对我们的运算要求较高，而方法2 是将椭圆问题转化为圆的问题来处理，由于圆具有很强的几何性质，所以问题得到了简化．另外，解法2 充分彰显了椭圆和圆之间的内在联系，也揭示了问题的几何本质和命题背景．

小结变换的实质是对应,通过变换可以揭示不同问题之间的内在联系，从整体上来把握数学问题．高中阶段常见的变换有：平移、对称、旋转、伸压等等，通过这些变换，可以化山重水复为柳暗花明，降低计算难度，明晰解题方向，优化解题过程，可以将陌生问题熟悉化、将复杂问题简单化．变换解题体现了数学中的转化思想，同时也彰显了数学的神奇和魅力！

波利亚说过：“如果我们不将题目变更，就几乎不能有什么进展，当原问题看起来不可解时，你不要忘记了人类的高明之处，就在于会迁回绕过不能直接克服的障碍，就在于能想出某个适当的辅助问题，会更自觉地变更题目．”