玩转高考真题——三角函数图象与性质

苏 玖

真题再现 （2021·全国甲卷理科第16 题）已知函数f(x)=2cos(ωx+φ)的部

思维延伸：本题考查三角函数的周期性、对称性、最值等性质，以及如何通过三角函数图象判断函数值的大小，从而得出不等式的最小正整数解.

改编1

原题可由图象求解析式，解析式的表达方式不唯一，如2020年新高考山东卷第10 题（多选题），于是可改编为：

（多选题）已知函数f(x)=2cos(ωx+φ)的部分图象如图1所示（见真题图），则2cos(ω x+)φ=（ ）

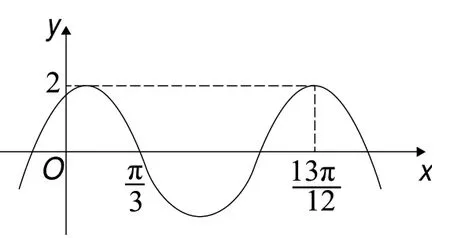
图1

点拨：此题关键是要读懂图提供的信息，如周期是怎样体现出来的？如何刻画最高点或最低点？对称中心在哪里？然后再求出相关参数的值．

改编2

也可以将三角函数图象与三角形的相关几何量结合，得到：

已知函数f(x)=Asinωx(A＞0,ω＞0)的部分图象如图2所示，点A，C是两个相邻的最高点和最低点，点B为对称中心，O为坐标原点，OA⊥AC，且△AOC的面积为8．（1）求f(x) 的解析式；（2）求不等式(f(x)-f(-6))(f(x)-f(12))＞0最小正整数x的值．

图2

点拨：如果从函数的解析式上出发求解不等式，运算量较大，但可以利用函数图象找出不等式的最小正整数解．

改编3

如果结合函数图象变换再求新函数的单调区间，于是有：

已知函数f(x)=Asinωx(A＞0,ω＞0)的部分图象如图所示，点A，C是两

个相邻的最高点和最低点，点B为对称中心，O为坐标原点，OA⊥OC，且△AOC的面积为（1）求f(x)的解析式；（2）将f(x)的图象上各点的纵坐标不变，横坐标伸长为原来的倍，将所得到的函数图象向右平移个单位长度，得到函数g(x)的图象，求g(x)的单调增区间．

图3

点拨：利用函数图象变换求出g(x)的函数解析式，根据正弦函数的单调增区间求出新函数的增区间．

改编4

可以将弦函数图象与圆结合，再进行图象变换，求新函数的值域或最值，如：

已知函数f(x)=Asinωx(A∈ N*,ω＞0)的图象在圆x2+y2=4 内至少有一个最大值点和一个最小值点．（1）求ω的取值范围；（2）当最小正周期T为最大正整数时，将f(x)的图象向左平移个长度单位，再将得到的图象纵坐标伸长为原来的2 倍，得到g(x)的图象，当时，求g(x)的值域．

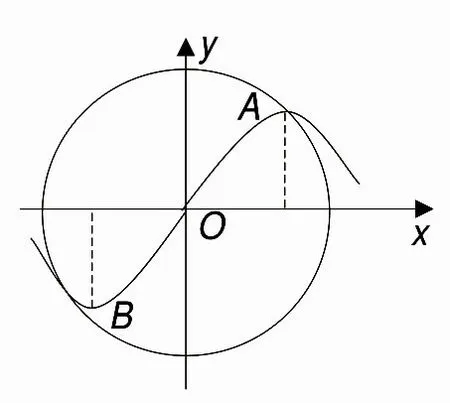
图4

点拨：根据弦函数的图象至少有一个最高点与最低点在圆内，可得振幅与周期的不等关系式，再根据振幅是正整数，可以确定T的范围，即可求出f(x)的解析式，从而求出g(x)的解析式，这样就得到值域．

改编5

也可以给出函数的奇偶性、单调区间和对称中心来确定解析式，如：

已知函数f(x)=Asin(ωx+φ) (A＞0,ω≠ 0)是偶函数，其图象关于点对称，且在上单调递增，求φ及ω的值．

改编6

如果已知函数的定义域和值域，又可以改编为：

已知函数f(x)=定义域为值域为[-1,5]，求a,b的值．

点拨:先利用二倍角公式和辅助角公式化简函数式，根据函数的最值，再利用分类讨论思想确定a与b的值．

改编7

若含有参数的三角函数图象对称性特征及经过特殊点都给出，结合三角函数求值问题又可以改编为：

已知函数f(x)=asinωx+bcosω x(ω＞0,ab≠0)的图象经过点和相邻两条对称轴之间的距离为

（1）求f(x)的解析式；

点拨:由三角函数图象性质可得相邻两条对称轴间的距离是半个周期，再结合图象过两个点建立方程组，求出解析式．根据已知锐角的组合式的三角函数值，利用拆角变换求出锐角的正弦值．

改编8

将三角函数的单调性与导数结合、图象与函数的零点结合，又可以改编为：

已知函数f(x)=2cos2x+(2a-1)sinx+a-2，（1）若f(x)在区间上单调递增，求a的取值范围；（2）是否存在整数a及正整数n，使f(x)在开区间(0,nπ)上有2 023 个零点？若存在，求出所有a及n的值；否则请说明理由．

点拨：首先利用导数研究函数的单调性，求出a的取值范围；其次利用因式分解，将函数零点转化为两个正弦函数图象与特定直线的交点个数问题，最后利用分类讨论思想和函数周期性求解．

回顾悟道：从一道填空题出发，结合三角函数图象与性质进行改编．

策略一：由诱导公式可知，同一三角函数图象可以有多个解析式，于是改编为多选题，如改编1；

策略二：根据三角函数图象的对称性与周期的关系，从三角形的特征出发（如面积、垂直等）进行改编，如改编题2-4；

策略三：根据函数图象经过定点来确定参数的取值，再变换为新函数，研究新函数的性质（如单调性、值域等），如改编题5-7；

策略四：研究函数式中参数的存在性问题，改编为探索性题目，如改编题8．

参考答案

真题：2

改编题：1.BC 2.（1）f(x)=2sin；（2）x=5．3.（1）f(x)=；（2）(k∈Z)．4.（1）；（2）．5.φ=2kπ-6.a=2,b=-1，或a=-2,b=5．7.（1）f(x)=2sin；（2）sinα=．8.（1）；（2）当a=0 时，n=1012；当a=1 时，n=1349.

扫一扫看详解

小试牛刀

高考真题（2021·北京卷理科第14题）若点P(cosθ,sin)θ与点关于y轴对称，写出符合题意的一个θ值：_________．

命题意图：根据高考真题的题型——开放型，引导编拟关于三角问题中开放型试题，培养发散性思维能力．

改编提示：（1）从奇偶性角度改编；（2）从值域确定解析式不唯一视角改编；（3）给出条件写出一个解析式；（4）从参数取值不唯一改编成多选题．