高中数学知识与方法大梳理（四）

龙艳文

幂函数、指数函数、对数函数

类型一：幂函数的图象和性质

例如图所示，图中的曲线是幂函数y=xn在第一象限的图象，已知n取±2，四个值，则相应于C1，C2，C3，C4的n依次为（ ）

[方法总结]

解决幂函数图象问题应把握的两个原则：

（1）依据图象高低判断幂指数大小，相关结论为：

①在(0,1)上，指数越大，幂函数图象越靠近x轴（简记为指大图低）；

②在(1,+∞)上，指数越大，幂函数图象越远离x轴（简记为指大图高）．

（2）依据图象确定幂指数α与0,1 的大小关系，即根据幂函数在第一象限内的图象（类似于y=x-1或或y=x3）来判断．

类型二：指数函数的定义域、值域、单调性的应用

例1（1）函数y=ax-2+1(a＞0 且a≠1)的图象过定点___________．

（2）函数y=2x+b的图象不经过第二象限，则实数b的取值范围是____________．

例2（1）不等式的解集是____________．

例3（1）解方程：4×4x-5×2x-6=0．

（3）已知9x-10 · 3x+9 ≤ 0，求函数y=a2x-ax+1（a>0 且a≠1）的最大值．

[方法总结]

方法：（1）指数方程与不等式问题关键是两边化同底．

（2）与指数函数有关的值域问题，

方法一：复合函数法，转化为利用指数函数的单调性；

方法二：换元法．

注意：若底数为字母，则需考虑分类讨论．

例4已知函数

（1）证明：f(x)在(-∞,+∞)上单调递增；（2）若f(x)为奇函数，求实数a的值．

类型三：对数函数定义域、值域、单调性应用

例1（1）当a＞0 且a≠1 时，函数y=1+logax的图象必定过定点____________．

（2）函数y=logax和的图象关于____________对称．

例2（1）求下列函数的定义域．

①y=；②y=

（2）方程log2x+log2(x-3)=2的解为_______________．

[方法总结]

方法：解对数不等式和方程关键两边化同底．

注意：考虑对数的定义域或最后检验．

化同底的方法：0=loga1；1=loga a=a0；M=logaaM=alogaM．

例3（1）已知函数则它的值域为____________．

（2）若函数f(x)=logax在区间[a,2a]上的最大值是最小值的3 倍，求a的值．

（3）求函数f(x)=(log2x)2-2log2x+3,x∈[1,4]的值域．

[方法总结]

方法：与对数有关的最值问题，利用单调性或换元．

注意：考虑定义域和分类讨论．

例4（1）函数y=log2(x2-4x-5)的单调区间为__________．

[方法总结]

方法：与对数有关的单调性，利用复合函数，结合图象分析．

注意：考虑定义域和分类讨论．

例5（1）已知函数y=(x2-mx+2)的定义域为R，则实数m的取值范围为__________．

（2）已知函数y=(x2-mx+2)的值域为R，则实数m的取值范围为____________．

[方法总结]注意：比较两个问题的区别．

函数零点

类型一：函数零点判断问题

例1（1）函数f(x)=的零点个数为（ ）

A.3 B.2 C.1 D.0

（2）函数f(x)=x3-x2-1的零点所在的区间是（ ）

A.(0,1) B.(-1,0) C.(1,2) D.(2,3)

（3）函数f(x)=2x+x-4零点所在区间为（ ）

A.(0,1) B.(1,2) C.(2,3) D.(3,4)

（4）设f(x)=lnx+x-2，则函数f(x)的零点所在的区间为（ ）

A.(0,1) B.(1,2) C.(2,3) D.(3,4)

例2（ 1）函数f(x)=lgx-x零点的个数为__________ ；

（2）函数f(x)=2x-x2零点的个数为__________．

[方法总结]

方法1：转化为两个函数数形结合．

合理转化为两个函数的图象（易画出图象）的交点个数问题．两个函数的图象交点的个数，就是函数零点的个数．

注意：函数图象的变化趋势（如渐近线，趋近点等）．

方法2：利用零点存在定理．

利用函数零点存在定理进行判断，必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数的零点个数．

方法3：解方程．

函数零点问题转化为方程根的问题，即通过解方程，由方程是否有解来判断函数是否有零点，其中方程有几个解就对应着函数有几个零点．

类型二：函数零点的应用

例1已知函数f(x)=若方程f(x)=a有两个不相等的实数根，则实数a的取值范围是（ ）

例2已知函数f(x)=g(x)=f(x)+x+a，若g(x)存在2 个零点，则a的取值范围是（ ）

A.[-1,0) B．[0,+∞) C.[-1,+∞) D．[1,+∞)

例3已知函数f(x)=恰有三个零点，则实数m的取值范围是_________．

[方法总结]

方法：数形结合，合理转化为两个函数的图象（易画出图象）的交点个数问题．两个函数的图象交点的个数，就是函数零点的个数．

注意：函数图象的变化趋势（如渐近线，趋近点等）．

例4若函数f(x)=4x-2x-a，x∈[-1,1]有零点，则实数a的取值范围是_____．

例5若函数f(x)=2x--a的零点在区间(1,2)内，则实数a的取值范围是（ ）

A.(1,3) B.(1,2) C.(0,3) D.(0,2)

[方法总结]

方法1：转化为方程有解问题．

方法2：参变分离，即a=F(x)，则a的范围即为F(x)值域．

方法3：利用零点存在定理．

结论：已知函数y=f(x) 在区间(a,b) 上单调，若f(x) 在(a,b) 上存在零点，则f(a)f(b)<0．

注意：若y=f(x)在区间(a,b) 上不是单调函数，则上述结论不一定成立．

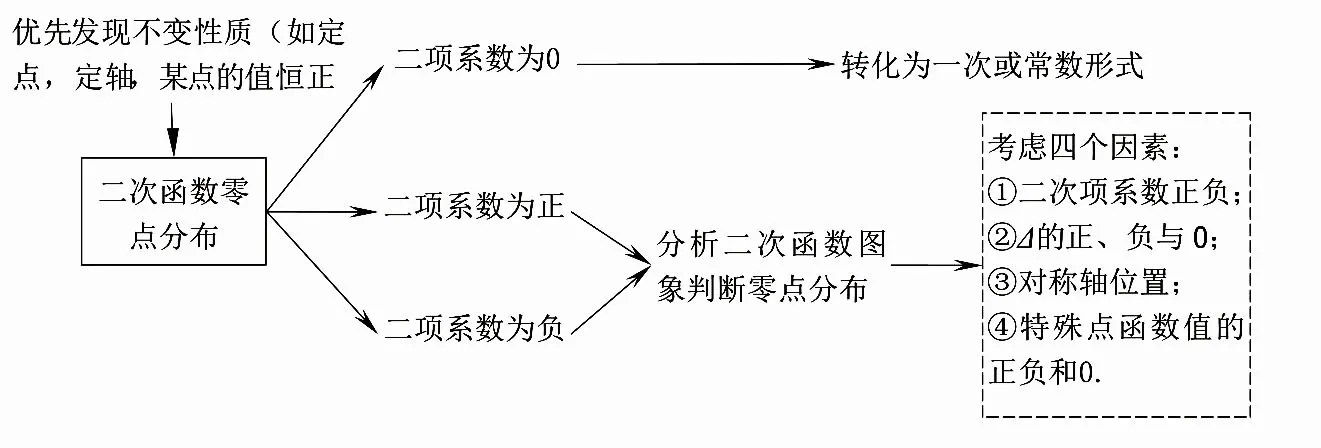
类型三：二次函数零点分布

例1（1）如果二次函数y=x2+mx+(m+3)在(0,+∞)上有两个零点，求m的取值范围．

（2）若方程x2-2ax+4a-3=0 的两根均大于1，求实数a的取值范围．

[方法总结]

方法1：韦达定理法，如对于二次方程根的分布情况．（两根与某一非零常数的关系同理）．

例2（1）求实数m的范围，使关于x的方程x2+2(m-1)x+2m+6=0．

①有两个实根，且一个比2 大，一个比2 小；②有两个实根，且都比1 大；③有两个实根α，β，且满足0<α< 1<β<4；④一根小于1，另一根大于2；⑤两根均在(1,4)之间．

（2）关于x的方程2kx2-2x-3k-2=0的两个实根一个小于1，另一个大于1，求实数k的取值范围．

（3）在下列条件下，分别求出m的取值范围．

①方程x2-mx-4=0 在[0,1]有解；②函数f(x)=x2-3x+4-m在[-1,1]上有零点．

[方法总结]

方法2：图象分析法