基于二阶滑模的永磁同步电机直接转矩控制研究

周志宇，文定都，张 阳，田其章，刘建华

（湖南工业大学 电气与信息工程学院，湖南 株洲 412007）

1 研究背景

永磁同步电机（permanent magnet synchronous motor，PMSM）结构简单、损耗小、效率高、电机形状及尺寸可灵活多样。随着材料技术的不断发展和性能提高，PMSM 已经在民用、航天和军事等领域广泛应用[1-2]。然而，PMSM 是个多变量、非线性和变参数的复杂对象，为获得较好性能，需对其采用一定的控制算法。

无传感器控制技术采用一定的控制算法实现转子位置及速度估算，这代表了PMSM 控制系统的发展趋势。目前常用的算法包括滑模观测器算法、模型参考自适应控制算法、扩展卡尔曼滤波器算法等[3]。其中，滑模观测器算法对系统模型精度要求不高，对参数变化和外部干扰反应不灵敏，但这种算法鲁棒性较强。在PMSM 控制系统中，该算法是基于给定电流与反馈电流间的误差设计滑模观测器（sliding mode observer，SMO），通过该误差重构电机的反电动势，估算转子速度[4-5]。而实际控制量是不连续的高频切换信号，为获得连续的扩展反电动势估计值，需外加一个低通滤波器，采用反正切函数来获得转子的位置信息。

传统的直接转矩控制（direct torque control，DTC）采用两个Bang-bang 控制器分别对转矩与磁链进行控制，响应速度较快、对系统参数变化和外干扰鲁棒性较强，但逆变器不稳定的开关频率，导致一个数字控制周期中所选用的有效电压矢量无法与期望的电压矢量一致，使得传统DTC 中磁链和转矩脉动过大[6]。为获得连续且更多的电压矢量，保证逆变器开关频率的恒定，本研究采用空间电压矢量脉宽调制（space vector pulse width modulation，SVPWM） 方法，同时引入二阶滑模控制器，构建转矩与磁链调节器[7-8]。基于理论与系统仿真分析表明，该算法控制精度高，抗干扰性强，增强了系统的鲁棒性。

2 PMSM 数学模型

为了简化分析，假设永磁同步电机在以下理想情况的基础上建立简单可行的数学模型：1）忽略铁芯的饱和；2）忽略电机中的涡流和磁滞损耗；3）电机中电流为对称的三相正弦波电流。

根据电机理论，将同步旋转坐标系下的方程利用反Park 变换，可得静止坐标系下的方程：

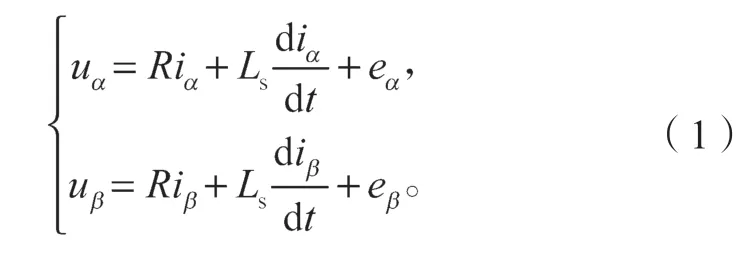
式中：uα、uβ为静止坐标系下的定子电压；iα、iβ为定子电流；R、Ls分别为定子电阻与定子电感；eα、eβ为静止坐标系下的反电动势，具体公式为

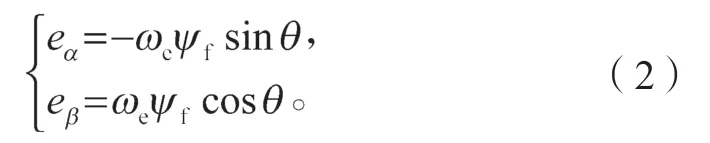
式中：ωe为电角速度；ψf为永磁体磁链；θ为转子角度。

根据式（1）可得出PMSM 在静止坐标系下的电流模型：

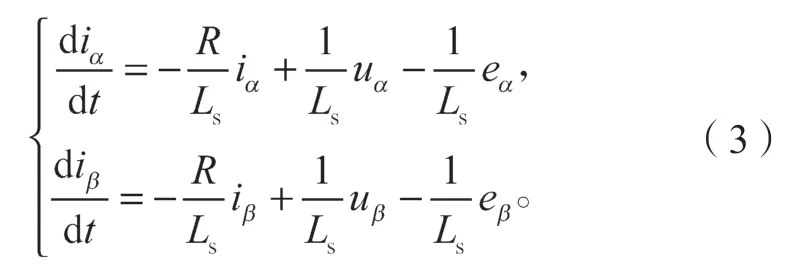
3 系统设计

3.1 滑模控制器的设计

3.1.1 速度控制器的设计

PMSM 是一个非线性、强耦合的多变量系统。控制系统受到外界扰动的影响，电机内部参数发生变化时，传统的PI 控制方法并不能满足实际要求[9]。因此，为提高PMSM 调速系统的动态品质，本研究利用滑模控制器（sliding mode control，SMC）对扰动与参数不敏感、响应速度快等优点，设计采用滑模速度控制器。以表贴式PMSM 为例，建立同步旋转坐标系下的数学模型如下：

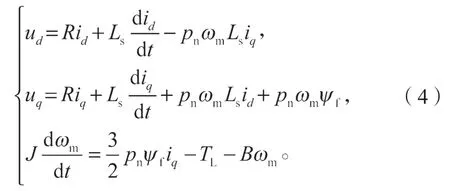
式中：ud、uq分别为定子电压的d-q轴分量；id、iq分别为定子电流的d-q轴分量；ωm为角速度；pn为电机相数；J为转动惯量；TL为负载转矩；B为转矩阻尼系数。

当id=0 时，转子磁场定向控制方法可以获得较好的控制效果，数学模型变为

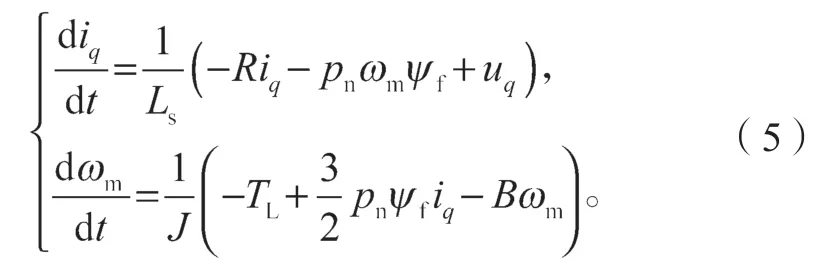
电磁转矩方程为

定义永磁同步电机系统的状态变量方程为

式中：ωref为电机的参考转速；ωm为实际转速。

根据式（5）～（7），联立求解可得方程组：

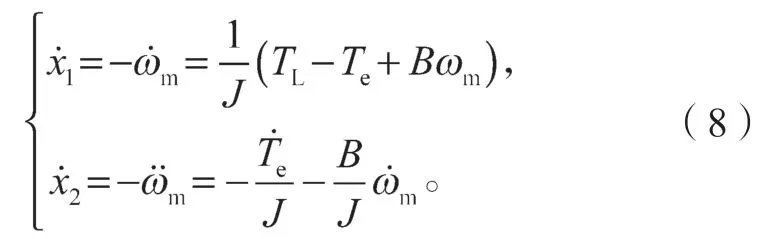
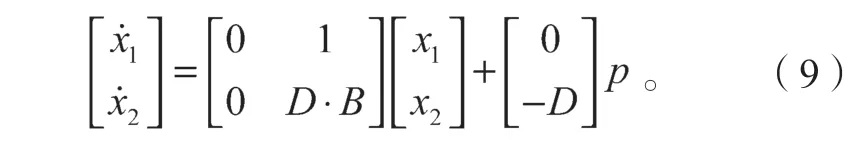
定义滑模面函数为

式中，c为设计参数，且c＞0。

对式（10）求导，可得出：

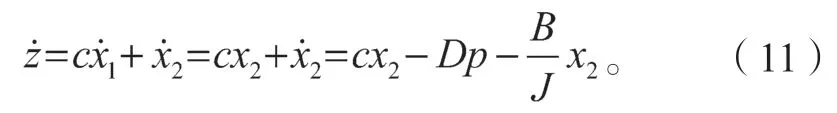
本研究采用指数趋近率，可得：

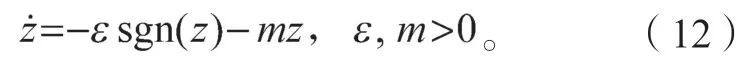
为了从根本上避免或削弱系统抖振，采用准滑动模态控制。将继电特性连续化，用连续函数θ(z)取代sgn(z)，可得：

为保证PMSM 驱动系统有良好的动态品质，定义控制器的表达式如下：

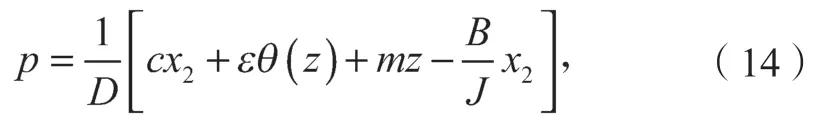
参考转矩为

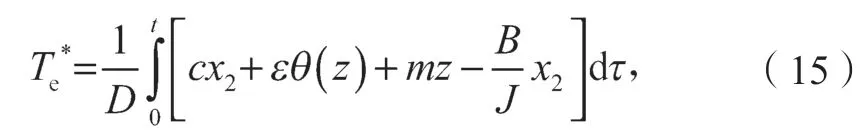
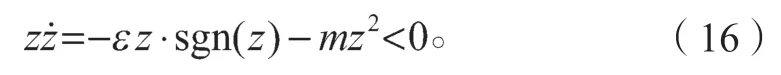
容易验证在滑模控制器的作用下，系统逐渐趋于稳定。

3.1.2 直接转矩控制器设计

同步旋转坐标系d-q下，求解电磁转矩Te的表达式为

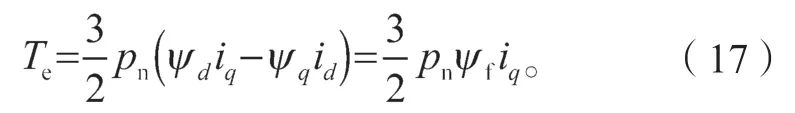
定子磁链矢量的方向与d轴方向相同时，ψr=ψd，定子磁链幅值可表示为

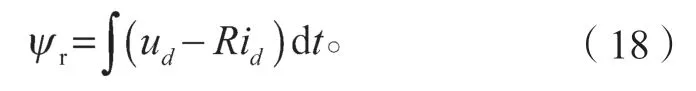
在二阶滑模控制算法中，对于一个动态系统，其表达式如下：

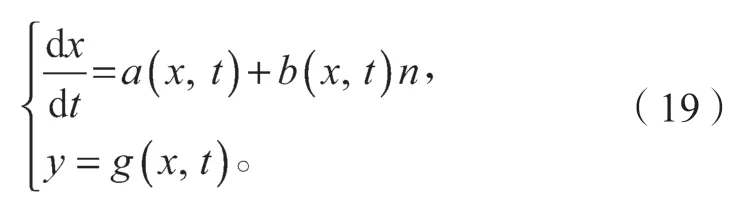
式中：n为输入变量；y为输出量；a、b、g为未知函数。

在二阶滑模控制中，一个为不连续的滑动变量函数，另一个为连续的导函数：

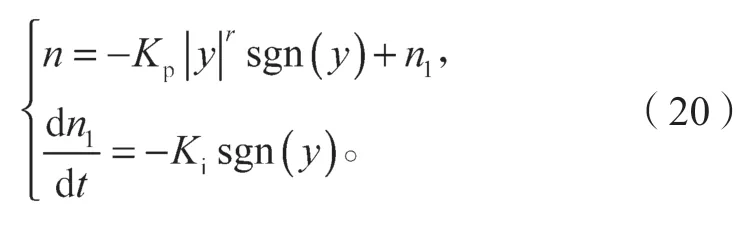
定义磁链的滑模面函数为

利用二阶滑模控制原理，此时磁链控制器的表达式为

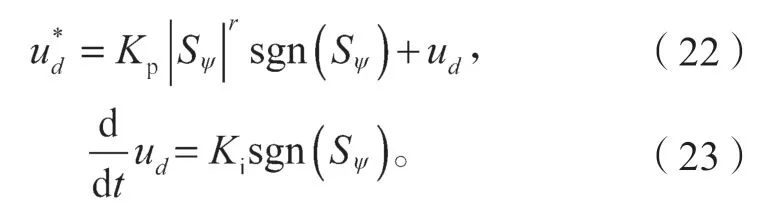
式中Ki、Kp为待设计参数，且Ki、Kp＞0。

同样，利用二阶滑模原理，此时转矩控制器的表达式为

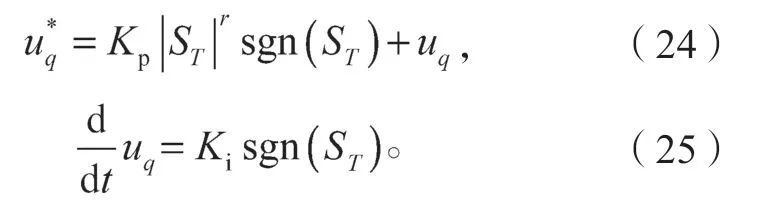
式中ST为转矩的滑模面函数。

令设计参数r=0.5，基于滑模控制的DTC 控制框图如图1 所示。

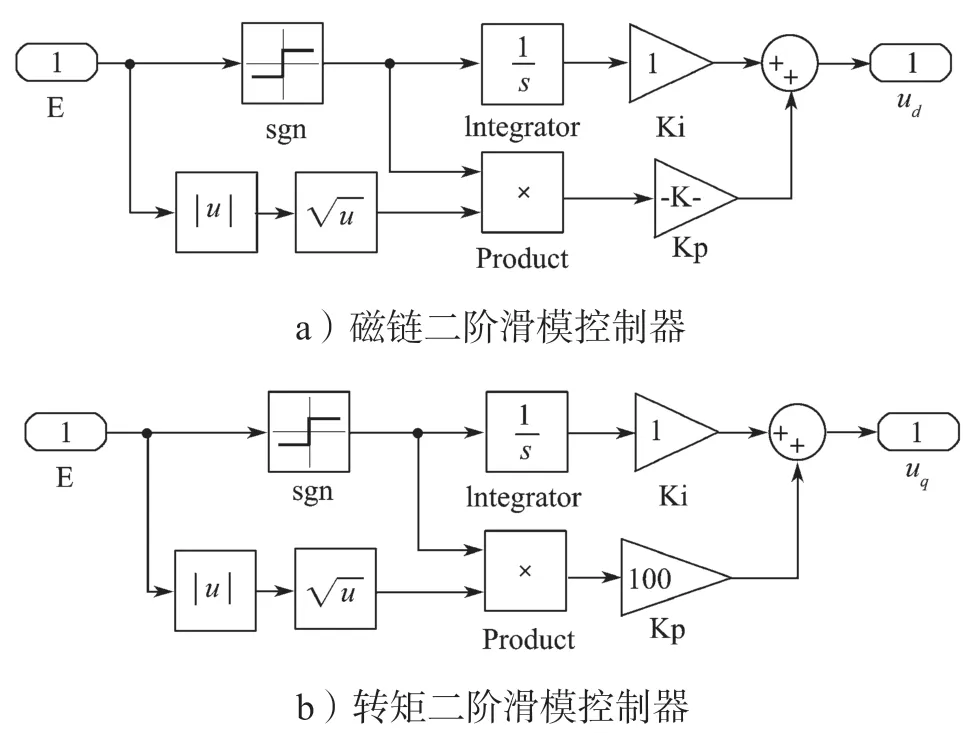
图1 基于二阶滑模的DTC 控制框图Fig.1 DTC control block diagram based on second order sliding mode

3.2 滑模观测器的设计

滑模控制系统是一种特殊的非线性控制系统，它与常规控制的根本区别在于控制的不连续性，即一种使系统“结构”随时变化的开关特性[10-11]。这种方法实现的关键在于滑模面函数的选取和滑模增益的选择，既要保证收敛的速度，又要避免增益过大引起电机运行产生过大抖振[12]。在PMSM 控制系统中，该方法是基于给定电流与反馈电流间的误差，并由该误差来重构电机的反电动势、估算转子速度[13]。

3.2.1 电流滑模观测器的搭建

电流SMO 算法的设计是基于静止坐标系下的数学模型，电机方程为

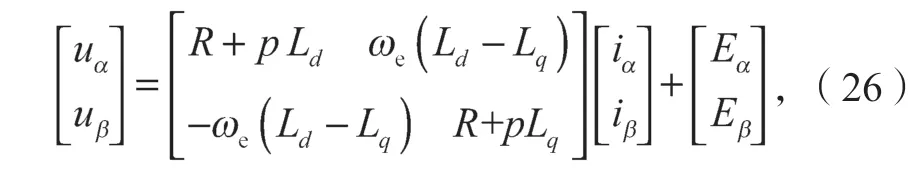
式中[EαEβ]T为反电动势，其表达式为

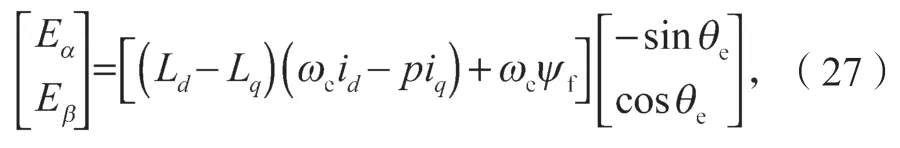
为方便观察扩展反电动势，将式（26）的电压方程改写为电流方程

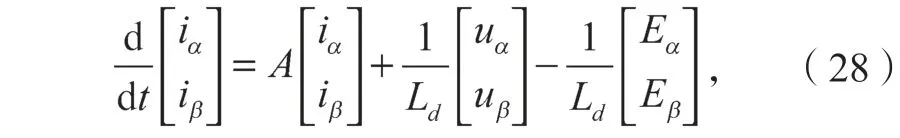
为获得扩展反电动势的估计值，设计电流滑模为

将式（28）与式（29）作差，可得出电流的误差方程为

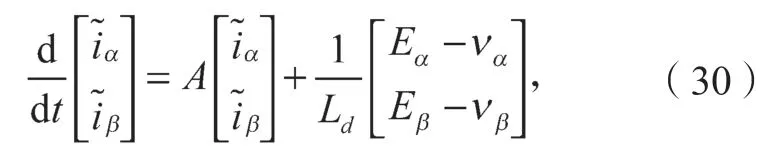
滑模控制率设计为

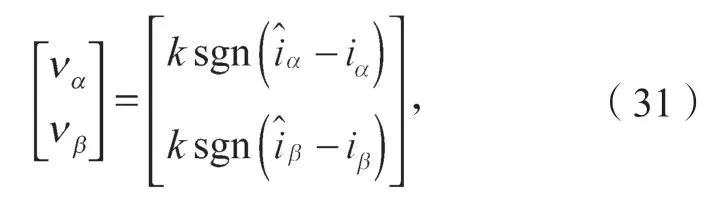
式中：

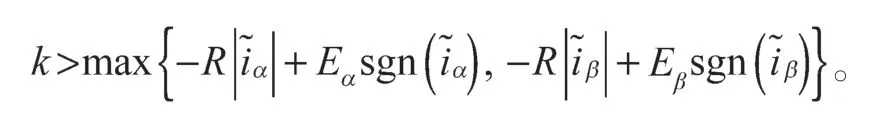
观测器的状态变化达到滑模面后，观测器状态会一直保持在滑模面上，根据滑模控制基本原理，可得：

3.2.2 反正切函数的转子位置估计

实际控制量为不连续的高频切换信号，为提取连续的扩展反电动势估计值，需要加一个低通滤波器：

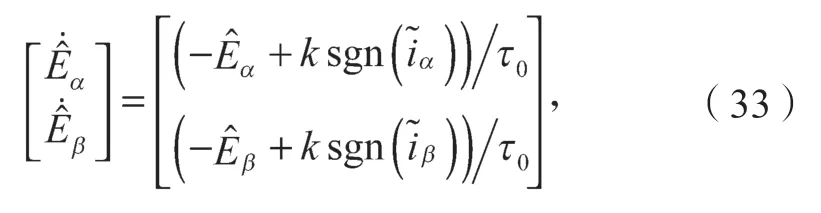
式中τ0为低通滤波器时间常数。

在进行低通滤波处理时，滤除高频切换信号的同时，扩展反电动势的估计值也会相应变化，本研究采用反正切函数获得转子位置信息：

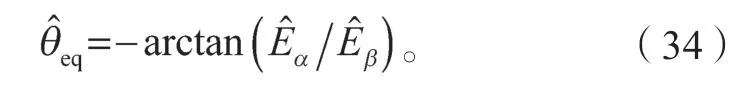
滤波处理获得的反电动势估算分量会引发相位延迟，通常需要在式（34）基础上加一个角度补偿，如式（35）所示：

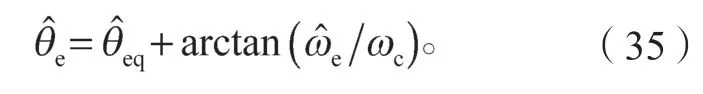
式中ωc为滤波器的截止频率。

反正切SMO 算法的实现原理框图如图2 所示。

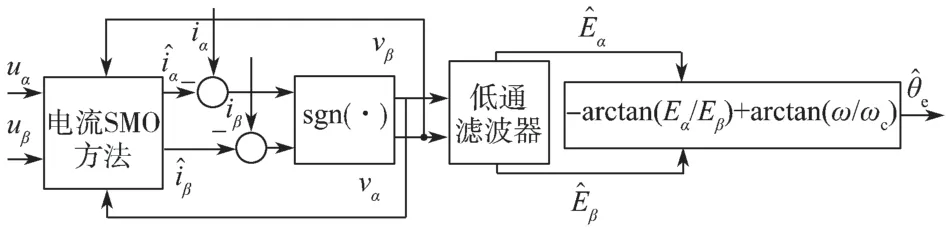
图2 反正切SMO 原理框图Fig.2 Principle block diagram of arctangent SMO

4 系统建模仿真与结果分析

4.1 仿真模型的搭建

根据文中算法描述，在Matlab/Simulink 环境下搭建仿真模型，以此验证基于二阶滑模的PMSM 直接转矩控制系统在动静态性能上的优势。其系统框图如图3 所示。

图3 基于二阶滑模的永磁同步电机直接转矩控制框图Fig.3 Direct torque control block diagram of permanent magnet synchronous motor based on second order sliding mode

根据滑模控制器的原理，滑模速度控制环仿真模型如图4 所示，其中的参数设置为c=60、ε=200、m=300。

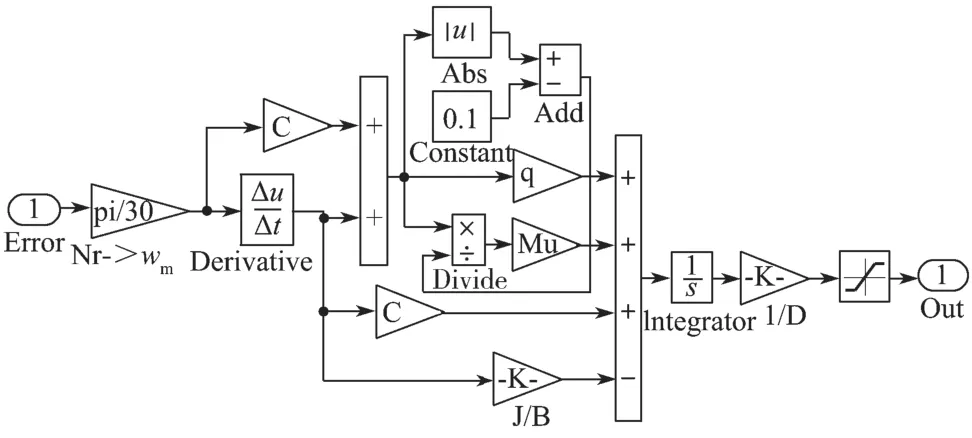
图4 滑模速度控制器仿真模型Fig.4 Simulation model of sliding mode speed controller

反正切观测器仿真模型如图5 所示，基于反正切函数部分仿真模型如图6 所示。基于二阶滑模的永磁同步电机直接转矩控制系统仿真模型如图7 所示，永磁同步电机的参数设置如表1 所示。其中的仿真的条件为Vdc=311 V，SVPWM 的开关频率为10 kHz，仿真运行时间为0.4 s。

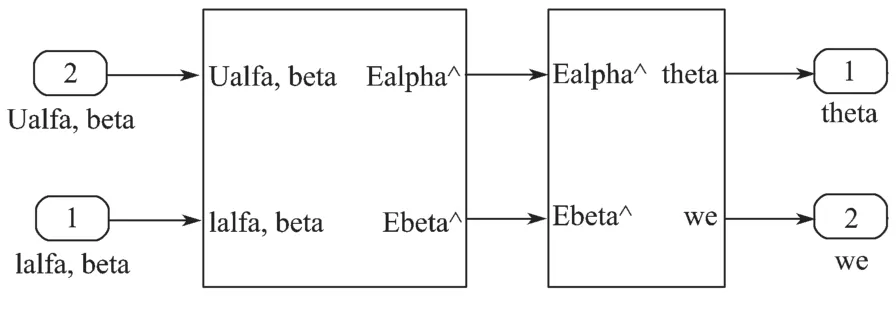
图5 反正切观测器仿真模型Fig.5 Simulation model of arctangent observer

图6 滑模观测器中使用反正切函数仿真模型Fig.6 Simulation model use arctangent function in sliding mode observe

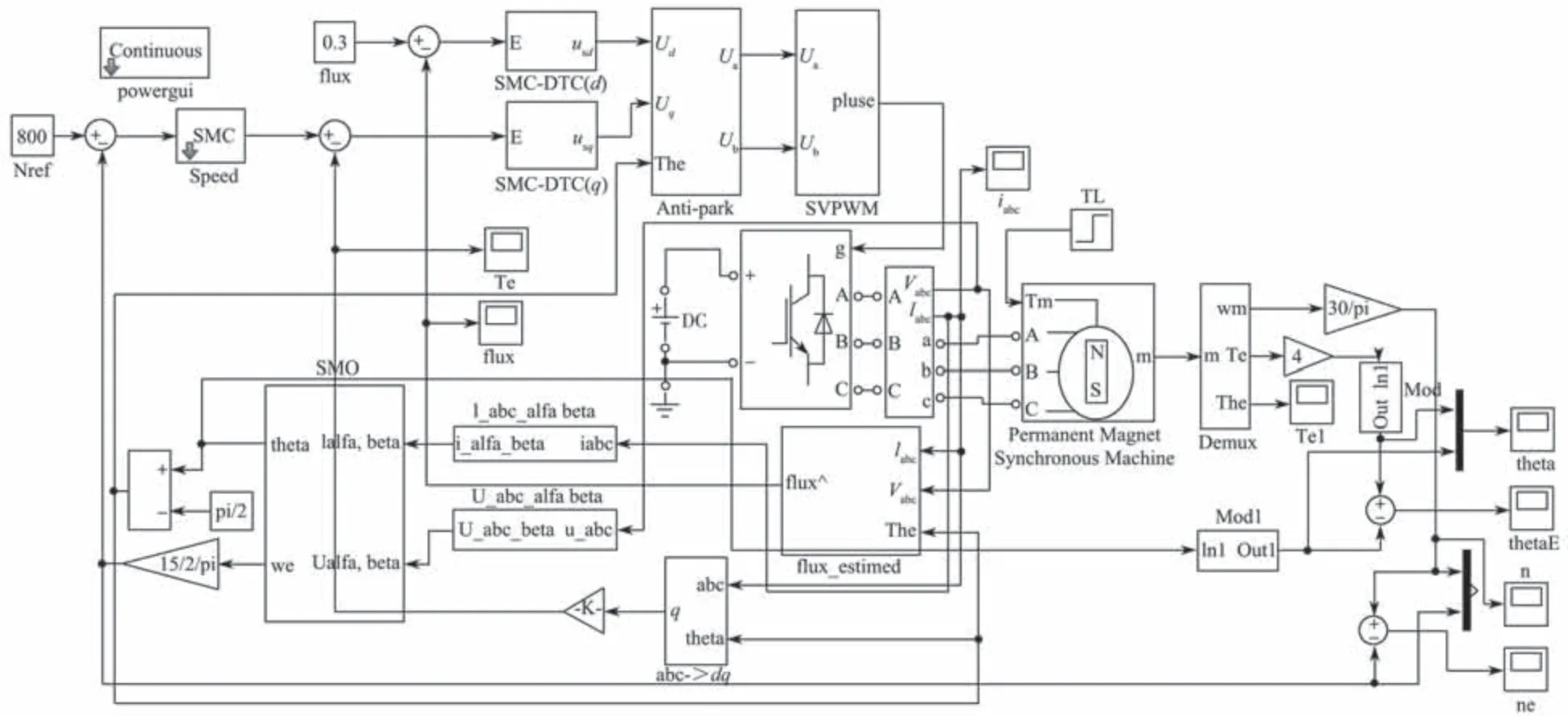
图7 基于二阶滑模的永磁同步电机直接转矩控制系统仿真模型Fig.7 Simulation model of PMSM direct torque control system based on second order sliding mode

表1 永磁同步电机参数Table 1 Parameters of permanent magnet synchronous motor

4.2 仿真结果与分析

永磁同步电机传统直接转矩控制和基于二阶滑模的永磁同步电机直接转矩控制仿真结果如图8～11所示。由图8a、b 所示传统直接转矩系统转速波形与改进后的控制系统转速波形可以看出，与传统直接转矩控制相比，改进后的转速观测值较为稳定，超调量基本为0。

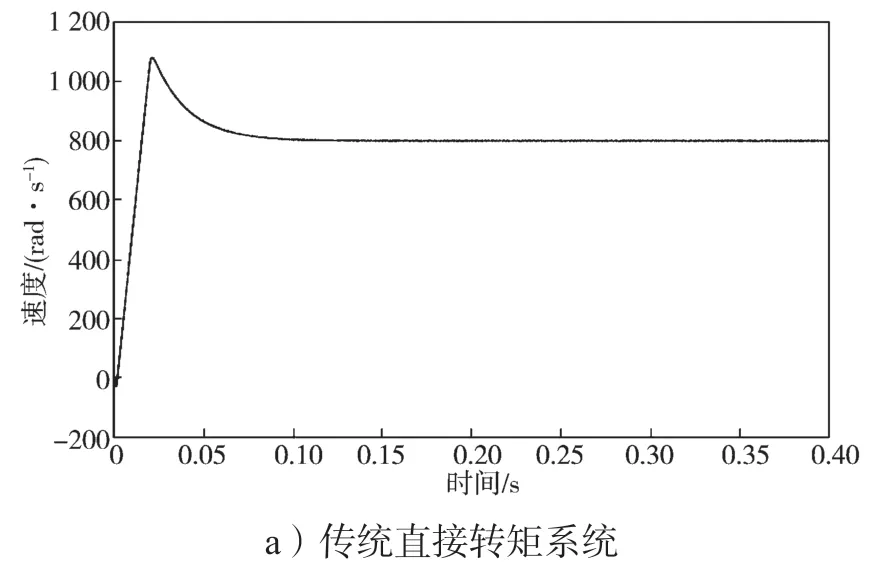
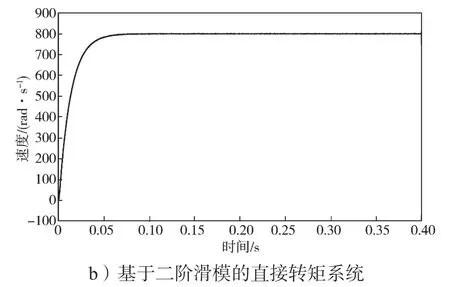
图8 系统转速波形Fig.8 System speed waveform

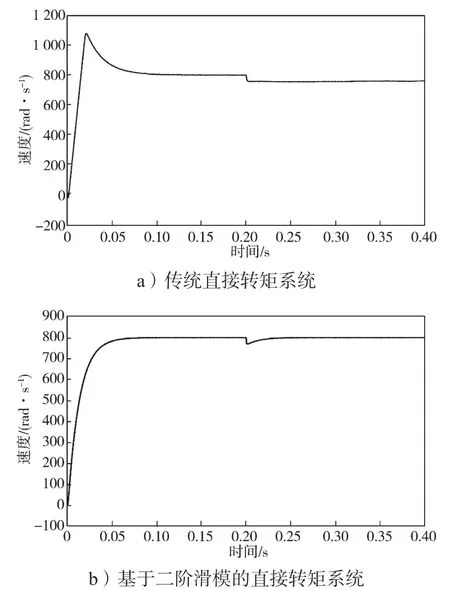
图9 TL=5 N·m 时的系统转速波形Fig.9 System speed waveform with TL =5 N·m

由图9 可看出，系统动态加载5 N·m 时，传统的直接转矩转速波形波动十分明显，超调量σ接近10%，调节时间为0.07 s，而改进后的控制系统转速波形响应速度快且超调量σ接近0，调节时间为0.055 s。在0.2 s 后，传统直接转矩由于负载较大，无法恢复到额定转速，而改进后的控制系统能在较短时间内恢复到额定转速，表明系统的抗干扰能力增强。

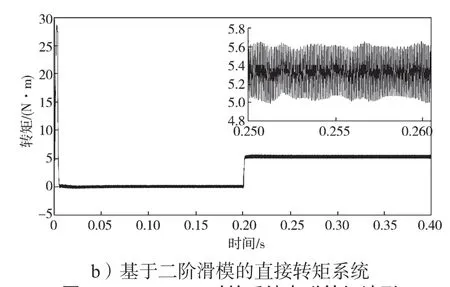
图10 TL=5 N·m 时的系统电磁转矩波形Fig.10 system electromagnetic torque waveform with TL =5 N·m

由图10 可以看出，选取[0.250 s，0.260 s]时间段观察，传统直接转矩波动范围为4.0～5.5 N·m，转矩波动为1.5 N·m，而改进后的系统转矩波动范围为5.0～5.6 N·m，转矩波动为0.6 N·m，可见转矩波动范围明显减小。

图11 系统磁链波形图Fig.11 Flux linkage waveform of system

由图11 可看出，传统直接转矩控制系统的磁链波动为0.294～0.304 Wb，磁链脉动为0.01 Wb，而改进后的系统磁链波动范围为0.297～0.301 Wb，磁链脉动为0.004 Wb，可见磁链波动范围也明显减小，这样电机抖动噪声比明显减小。

根据上述的仿真曲线与分析可知，传统直接转矩控制系统产生的超调量比较大，响应时间比较长，抖振严重；改进后的基于二阶滑模直接转矩控制系统产生的超调量小，响应时间短，抖振很小，抗干扰性能强，具有较强的鲁棒性能。

5 结语

本研究提出了一种基于二阶滑模的直接转矩控制系统。用SVPWM 空间矢量脉冲宽度调制技术代替滞环控制与开关表，获取了更多连续的电压矢量，使逆变器的开关频率得到控制。采用二阶滑模控制器调节磁链和转矩，减少了电机参数与外界干扰对磁链和转矩控制的影响。仿真实验结果表明：基于二阶滑模的直接转矩永磁同步电机调速系统，在超调量、调节时间、转矩和磁链脉动上，都优于传统直接转矩控制系统，能较好地消除抖振，提高了系统的抗干扰能力和鲁棒性能。