轨道非线性能量阱尖端效应分析及简化设计方法研究
张 超,郑雨强,王菁菁
(1.湖南工业大学 土木工程学院,湖南 株洲 412007;2.中国建筑第四工程局有限公司,广东 广州 510000;3.广州大学 土木工程学院,广东 广州 510006)
1 研究背景
结构控制技术通过对主体结构施加被动或主动的作用力,改变主体结构的刚度或阻尼以有效减小结构振动[1]。其中,调谐质量阻尼器(tuned mass damping,TMD)是工程结构中应用最为广泛的被动控制方法,一般被放置在主体结构顶层,当TMD 与主体结构相调谐时两者形成共振机制,从而减小主体结构响应[2-3]。但当主体结构受到损伤、沉降或其他因素影响时,结构自振频率发生变化,TMD 与之失谐而导致减振性能退化,甚至会增大结构响应[4]。
为了解决TMD 对结构变化频率敏感的问题,有学者提出非线性的结构控制方法——非线性能量阱(nonlinear energy sink,NES)[5]。 国 外 学 者S.Aubry[6]、G.Kopidakis[7]等的研究表明,与TMD 相比,NES 的非线性力-位移使其能够在宽频范围内发生共振,降低结构响应,其频率鲁棒性能优于TMD。此外,国内学者也对NES 进行了相关的研究,如张也弛等[8]使用数值方法研究了两自由度NES 在简谐荷载下的力学特性和振动控制效果。王菁菁等[9-11]提出了一类新型被动质量阻尼器——轨道非线性能量阱,该装置由轨道和附加质量块组成,如图1 所示。通过轨道形状实现非线性恢复力,轨道固定在主体结构顶层,质量块沿轨道运动,如图2 所示。Wang J.J.等[12]研究了两自由度主体结构附加轨道NES 在脉冲荷载作用下的减振性能,实现了具有近似3 次方恢复力的轨道NES。同时,研究发现轨道NES 的力-位移关系中产生尖端效应,这是轨道NES 特有的现象,未见于其他类型的NES。尖端效应是指当NES 质量块位移较大、轨道斜率极大时,恢复力随着位移的增大反而减小。当无尖端效应发生时,轨道NES 的减振效率难以达到最佳;当存在一定程度的尖端效应时,轨道NES 的减振效率较好。尖端效应可以防止轨道NES 恢复力过大而造成局部构件发生破坏。
本研究对轨道NES 尖端效应进行理论推导,得到了轨道NES 尖端效应产生的主要原因,并分析了尖端效应的强烈程度。分别通过不同输入能量下的无阻尼轨道NES 的自由振动、有阻尼轨道NES 的受迫振动,对轨道NES 的尖端效应进行分析。根据所得到的分析结果,揭示了轨道NES 尖端效应产生的主要原因,从而提出了基于尖端效应的轨道NES 简化设计方法。
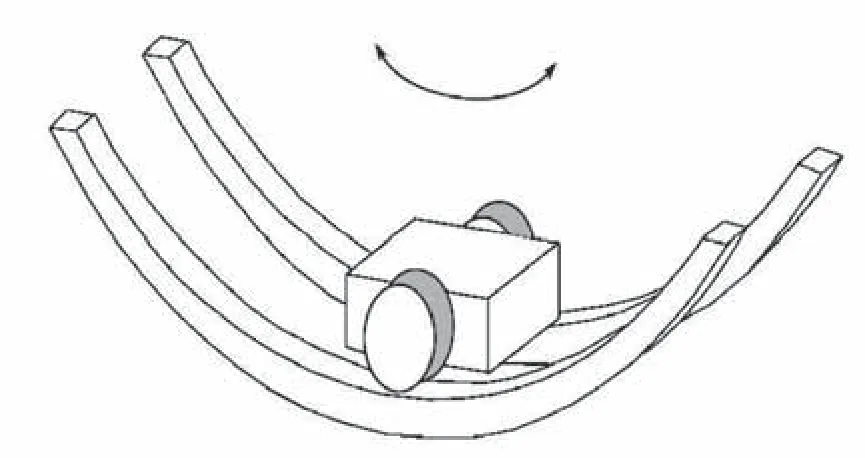
图1 轨道NES 示意图Fig.1 configuration of track NES
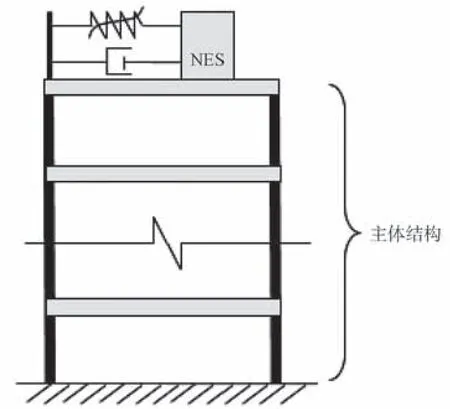
图2 轨道NES 系统示意图Fig.2 Illustration of track NES system
2 轨道NES 恢复力
轨道NES 的自由体受力示意图如图3 所示,其中,mN为NES 的质量,g为重力加速度,θ为轨道切线角度,FNormal为NES 作用在轨道上的法向力,uN和vN分别为NES 相对于轨道的水平位移和竖向位移,z为轨道的水平位移,h(uN)为轨道的形状函数,即NES 的竖向位移。
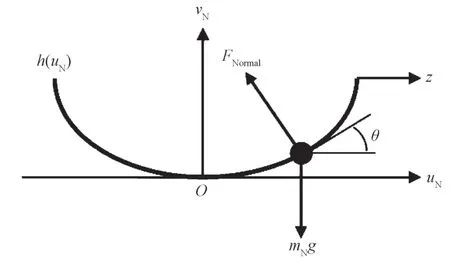
图3 轨道NES 自由体的受力示意图Fig.3 Force diagram of track NES
推导中假设NES 质量不发生转动且始终与轨道接触,采用牛顿方法可以得到轨道NES 的运动方程。根据图3 列出水平方向上的力平衡方程为

竖直方向上的力平衡方程为
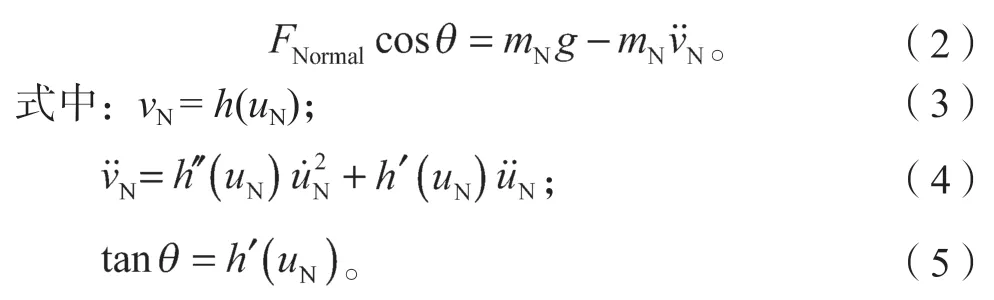
将式(3)和式(4)代入力平衡方程式(1)和式(2),并联立式(5)可得:
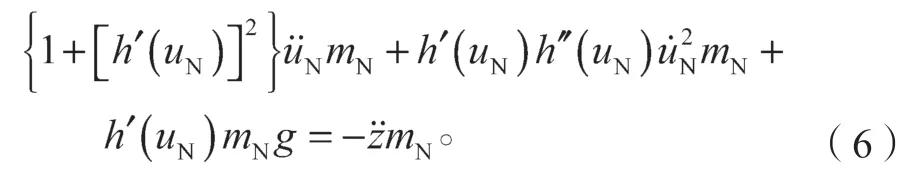
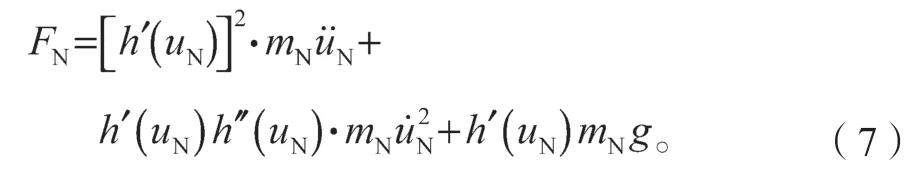
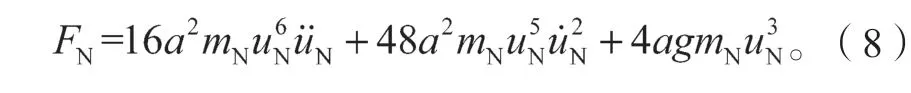
3 轨道NES 尖端效应理论推导
本节对轨道NES 尖端效应进行理论推导,得出了轨道NES 尖端效应的产生原因,分析了尖端效应的强烈程度。
在恢复力表达式(8)中,第一项和第二项分别与轨道NES 的加速度和速度有关,同时也与位移的高阶项有关,而第三项仅与位移相关。为了简便起见,将这3 项分别记为Fa、Fv和Fd,可得它们之间的关系如下:

式中:
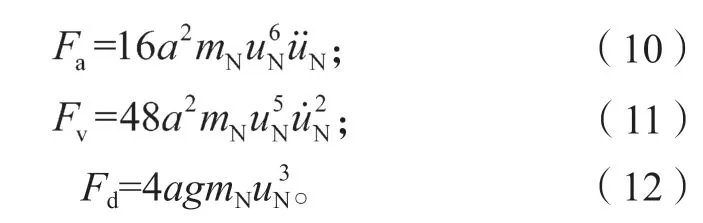
采用谐波平衡法进行分析,相关研究[13]中,当且仅当取一阶频率进行近似求解时所得结果与数值模拟结果吻合良好,因此,本文取一阶频率项进行分析。无阻尼轨道NES 的自由振动可以写成:

式(13)~(16)中:A为振动的振幅;ωN为根据式(16)定义的轨道NES 的瞬态自然频率;φN为振动的初相。
因此,恢复力可写成
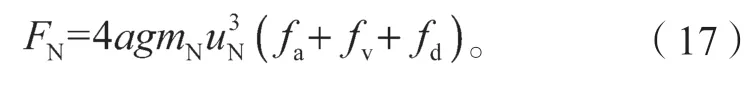
式中:
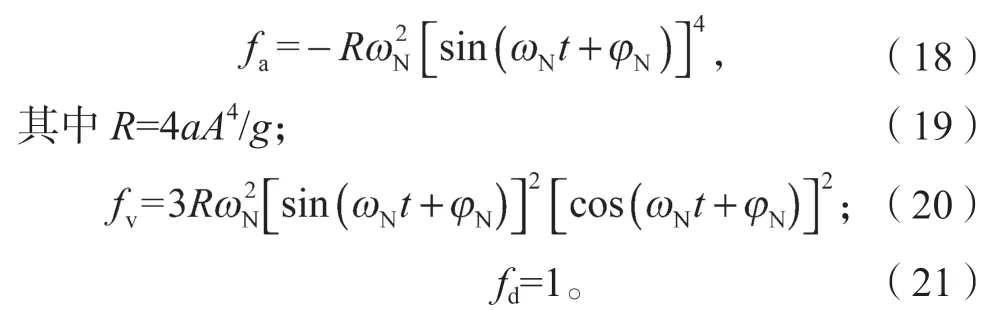
由于fd等于1,fa和fv表示Fa和Fv相对于Fd的作用力方向和大小比例。
分析式(18)~(21),可以得出:
1)由于R始终为正,因此fa为负,fv为正,这说明Fa始终与Fd方向相反,Fv始终与Fd方向相同。
2)R是与轨道NES 参数有关的常数。因此,当ωN非常小时,Fa和Fv的量级远小于Fd,可以在FN中忽略。此时FN≈Fd,且轨道NES 的瞬态自然频率变成

令
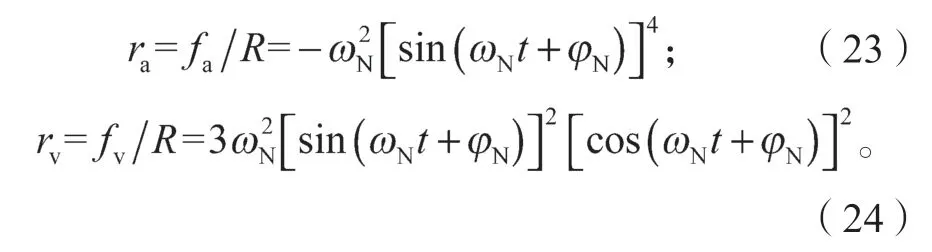
ra和rv是关于ωN的单变量函数,其函数图像如图4所示,可用于分析轨道NES尖端效应的强烈程度。
根据图4 所示曲线图可以得知:当φN=0 时(即对应初始位移为0,仅具有初始速度的自由振动)ra和rv随着ωN而变化。
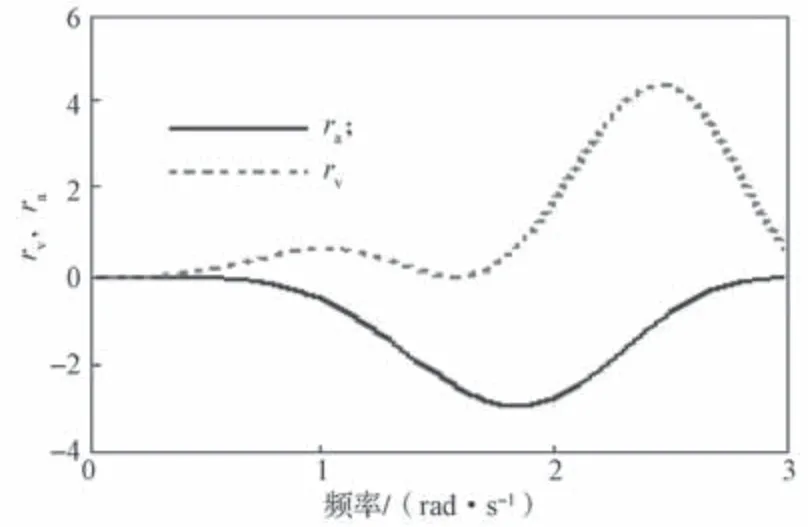
图4 ra 函数和rv 函数Fig.4 ra and rv as functions of ωN
根据观察可以推导得到有关轨道NES 恢复力的一些特点:
1)在rv曲线中,观察到其绝对值首次减小发生在ωN=1 rad/s,其频率低于ra绝对值首次减小时所对应的频率,ra和rv绝对值的减小表明了其对应分力Fa和Fv的减小。
2)轨道NES 的刚度随位移增大而增大,因此分力Fv减小所对应的位移小于分力Fa减小所对应的位移,表明Fv绝对值的减小早于Fa绝对值的减小,当各分力的减小程度不同步时会导致合力FN的大小发生上下波动,即产生尖端效应。
3)ra和rv的变化随着频率的增加而变得更加剧烈,表明在更大的位移处尖端效应更加显著。
4)随着Fv首次减小,FN中观察到尖端效应,而尖端效应发生后,随着位移的增加,ωN不增大反而减小,这使得Fa的减小太可能发生。
为了直观地说明轨道NES 的尖端效应,下面讨论无阻尼轨道NES 的自由振动和有阻尼轨道NES 的受迫振动,轨道形状均采用h(uN)=0.015uN4。
4 无阻尼轨道NES 尖端效应分析
图5 为NES 质量块的初始速度为0.42 m/s 时,无阻尼轨道NES 的加速度、速度和位移时程曲线图。
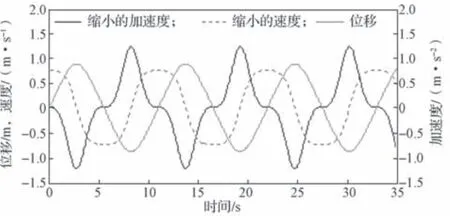
图5 0.42 m/s 初始速度下无阻尼轨道NES 的响应曲线Fig.5 Responses curve of undamped track NES at an initial velocity of 0.42 m/s
可以很明显地从图5 中得知振动频率,ωN,a=0.57 rad/s。同时,为了在同一张图中显示3 个运动变量的时程曲线,速度和加速度分别按进行缩小,缩小后的曲线如图5 所示。
图6 为图5 中的运动产生的恢复力FN及其分力Fa、Fv和Fd随位移变化的曲线图。从图6a 可以看出,Fa始终与Fd方向相反,Fv始终与Fd方向相同,这与第3 节中得出的结论相同。

图6 0.42 m/s 初始速度下无阻尼轨道NES 的力-位移关系曲线Fig.6 Force-displacement relationship curve of undamped track NES at an initial velocity of 0.42 m/s

此外,在所示运动的能量等级,Fa和Fv非常小并且与Fd相比可以忽略。fa和fv的大小可以将ωN,a=0.57 rad/s 代入进行计算,如式(26)和(27),均远小于fd=1。因此,式(22)可用于计算Fv在如式(28)所示的绝对值(ωN=1)处首次减小时,轨道NES 的位移,与图6c 所示的Fv峰值时的位移(约为0.75 m)相一致。然而,Fv的这种减小不会在FN中产生有效的尖端效应,因为此时负向分力Fa增加的速率远快于Fv,并且Fa和Fv都远小于Fd,不能使FN发生显著的变化。
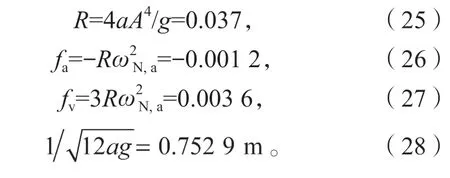
图7 和图8 分别描述了当自由体获得5 m/s 初始速度(输入能量相对较高)的无阻尼轨道NES 的运动状态时程曲线图和恢复力-位移关系曲线。图7 中,速度和加速度时程分别按1/ωN,a(ωN,a=1.53 rad/s)和进行缩小。在这种情况下,图8 中,Fa和Fv与Fd具有相同的数量级。在Fv中可以很清晰地观察到力随位移先增大后减小的变化,在位移的终端可以识别出在Fa中发生了微弱的尖端趋势,在FN中尖端效应显著。此时,由于FN与Fd已不再相同,式(22)不能在此处用于计算Fv达到峰值时的位移。

图7 5 m/s 初始速度下无阻尼轨道NES 的响应曲线Fig.7 Responses curve of undamped track NES at an initial velocity of 5 m/s
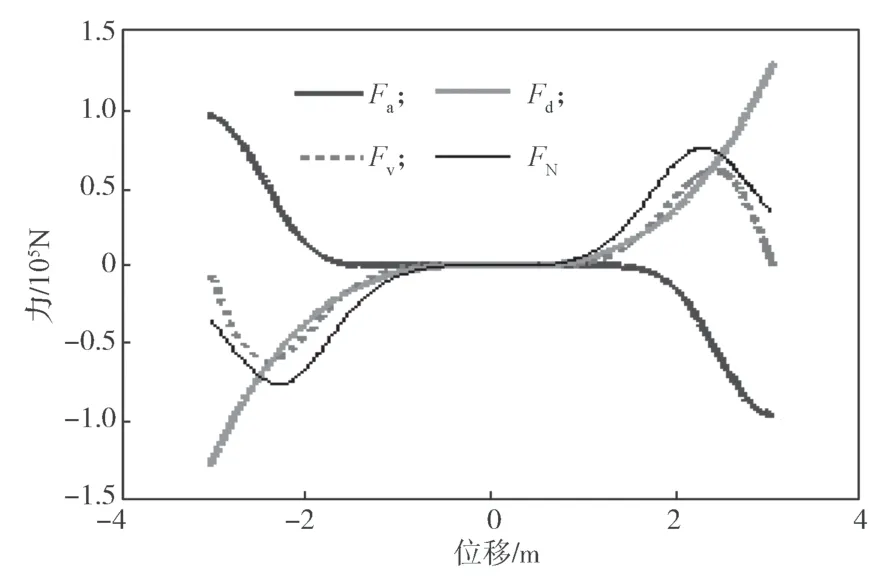
图8 5 m/s 初始速度下无阻尼轨道NES 的力-位移关系曲线Fig.8 Force-displacement relationship curve of undamped track NES at an initial velocity of 5 m/s
5 有阻尼轨道NES 尖端效应分析
图9 和10 分别是阻尼系数为1.7×105N·m/s 时,有阻尼轨道NES 附加在文献[14]中的32 自由度,主体结构顶层时的运动状态时程曲线图和恢复力-位移关系曲线图。主体结构每层以及NES 质量块的初始速度都为1 m/s。图9 中轨道NES 的运动以主体结构顶层运动为参考,即为两者的相对运动,并且速度和加速度时程曲线分别按1/ωN,a(ωN,a=1.58 rad/s)和进行缩小。由于轨道NES 中阻尼的存在以及主体结构运动的激励,轨道NES 的特性变得更加难以推测。Fv和Fa绝对值的减小每次都发生在不同的位移处,并且在尖端效应发生的位移范围内有小幅度波动。此示例定性地论证了图4 中的推论:Fv的减小比Fa的减小更容易发生,Fv是轨道NES 中产生尖端效应的主要原因,并且在较大的位移处尖端效应更加显著。
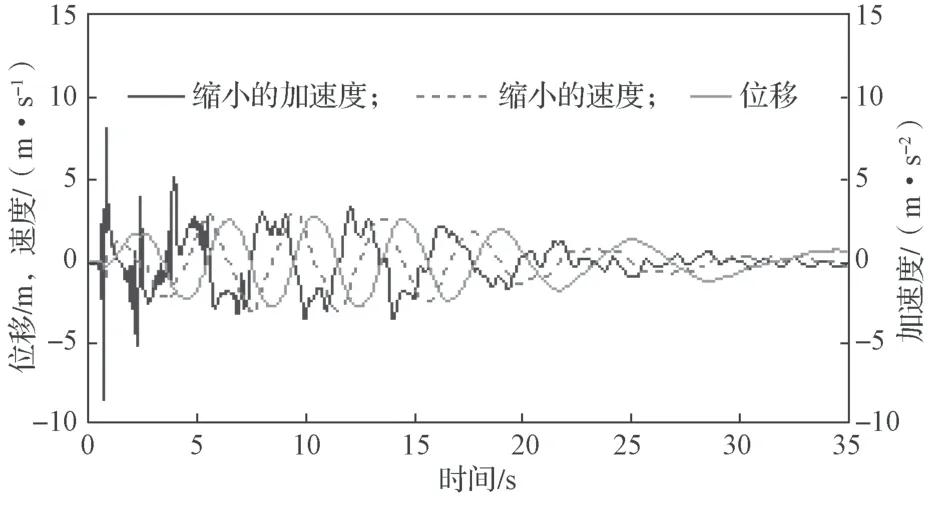
图9 基激励下有阻尼轨道NES 的响应曲线Fig.9 Responses curve of damped track NES under base excitation

图10 基激励下有阻尼轨道NES 的力-位移关系曲线Fig.10 Force-displacement relationship curve of damped track NES under base excitation
6 结论
尖端效应是轨道非线性能量阱的力-位移关系中存在的特有现象。本研究进行了尖端效应理论推导,分析了不同情况下轨道NES 的尖端效应,得出以下结论:
1)分力Fv减小所对应的位移小于分力Fa减小所对应的位移,表明Fv绝对值的减小早于Fa绝对值的减小,各分力的减小程度不同步导致合力FN的大小发生上下波动,即产生尖端效应。
2)无阻尼轨道NES 尖端效应分析结果表明,输入能量相对较低时,分力Fa和Fv非常小且与Fd相比均可以忽略。由于负向分力Fa增加的速率远快于Fv,且Fa和Fv都远小于Fd,不能使FN发生显著的变化,Fv的减小不会在FN中产生有效的尖端效应。输入能量相对较高时,在Fv中可以很清晰地观察到力随着位移先增大后减小的变化,在位移终端可以识别到在Fa中发生了微弱的尖端趋势,且在FN中尖端效应显著。
3)有阻尼轨道NES 尖端效应分析结果表明,Fv和Fa绝对值的减小每次都发生在不同的位移且在尖端效应发生的位移范围内有小幅度波动,可以定性地说明Fv的减小比Fa的减小更容易发生,Fv是轨道NES 中产生尖端效应的主要原因,在较大的位移处尖端效应更强。
基于上述结论:在Fv达到峰值以前,Fv和Fa的绝对值大小相近,且由于Fa和Fv的方向总是相反,Fd成为FN中最具有代表性的项,可采用Fd(式(12))作为其恢复力进行轨道NES 的初步设计。

