基于核诱导的不完整多视角聚类

张 炜，邓赵红，王士同

江南大学人工智能与计算机学院，江苏无锡 214122

随着数据采集技术的发展，数据的复杂性越来越高，复杂数据给传统机器学习技术带来许多挑战。数据的复杂性包括很多方面，如：数据集的大小、数据属性特征的复杂性等。观察复杂数据集时，可以通过多个视角诠释，多视角数据是指对同一样本不同角度的表示，例如在基于内容的网页图像搜索中，目标可以用图像的可视化特征以及对图像描述的文本特征表示。近年来，多视角学习得到越来越多的关注，在各个领域得到广泛应用。

多视角聚类作为多视角学习的重要分支，近年来取得了较大发展[1-2]。Cleuziou 等人基于经典模糊C 均值聚类（fuzzy C-means，FCM）算法，利用协同划分的思想对不同视角的模糊划分进行控制，提出了基于FCM 的协同聚类算法[3]。Liu 等人针对多视角数据，提出了一个新颖的张量框架，该框架用来在谱聚类中整合异构多视角数据[4]。Wang 等人提出了一种多视角学习模型，通过引入新的联合结构稀疏准则，将所有特征进行集成，并对每个特征的权值进行单独学习[5]。Xia 等人提出了一种鲁棒的多视角谱聚类的马尔可夫链方法，该方法通过低秩稀疏分解将每个视角的过度概率矩阵组合成一个共享的过度概率矩阵[6]。另外，近年来还有一些在非负矩阵分解（nonnegative matrix factorization，NMF）基础上的多视角聚类算法被提出[7-8]。Liu 等人提出了一个具有一致性约束的联合非负矩阵分解过程，该过程对每个视角执行非负矩阵分解，并利用每个视角的低维表示推出一个共同的表示[7]。基于NMF 和流形学习，Shen 等人提出了流形NMF[8]。

上述多视角聚类算法大多有一个共同的前提假设：所有视角都是完整的。然而在现实场景中，多数多视角数据存在缺失。例如，文本集群中，可以将文档翻译成代表多个视角的不同语言。但是，某些文档可能没有全部翻译版本。再例如视频数据中，画面和声音各代表一个视角，而有的数据只有声音视角或者画面视角。在这些情况下，传统多视角聚类算法将不可用或不再可靠，因此如何充分利用隐藏在不同视图中的互补知识，减少缺失实例的影响，是不完全多视角学习中最具挑战性的问题。

为了应对不完整多视角带来的挑战，近年来，一些不完整多视角算法被提出：Trivedi 等人提出了一种基于核相关性分析的不完整视角核矩阵补全的方法[9]，然而该方法需要至少一个视角的数据是完整的。Gao等人基于谱图理论和核对齐原理提出了IVC（incomplete multi-view clustering）[10]，但是，该方法不能处理缺失率较大的情况。Li等人通过使用NMF 和L1正则化提出了处理两个视角不完整数据的聚类算法（partial view clustering，PVC）[11]。Zhao 等在PVC的基础上，融合PVC 和流型学习提出IMG（incomplete multi-modal grouping）[12]。Hu 等人在PVC 的基础上引入半非负矩阵分解（semi-nonnegative matrix factorization，semi-NMF），提出了DAIMC（doubly aligned incomplete multi-view clustering）[13]。Shao 等人使用加权非负矩阵分解技术和L2,1正则化项提出了MIC（multi-view incomplete clustering）[14]。为了减少运算时间，Shao 等人又提出了在线不完整多视角聚类算法[15]。在PVC 的基础上，Wen 等人通过将最近邻图应用到矩阵分解的重构误差上提出了IMC_GRMF（incomplete multi-view clustering via graph regularized matrix factorization）[16]。此外，Wen 等人通过对所有视角的共性表示和相似图进行联合学习提出了IMSC_AGL（incomplete multi-view spectral clustering with adaptive graph learning）[17]。Wang 等人通过建立光谱摄动理论与不完整多视角聚类之间的联系，利用光谱聚类的关键特征，将特征值缺失转化为相似值缺失，提出了PIC（perturbation-oriented incomplete multi-view clustering）[18]。虽然目前上述这些方法显示出一定有效性，但仍存在一些问题：（1）上述这些不完整多视角算法大都是在欧式空间求解共性矩阵，然后利用共性矩阵进行聚类得到最终结果，然而多数多视角数据在原始特征空间并不线性可分，因此不能找到具有较好代表性的共性矩阵，并且在缺失样本的情况下找到具有较好代表性的共性矩阵难度大大增加。（2）不同视角提供可鉴别的信息量有所不同，因此在学习优化过程中平等对待每个视角是不合理的。（3）数据的局部几何结构没有得到很好的挖掘，不能保证得到的共性矩阵的紧凑性和代表性。因此，不完整的多视角聚类仍面临重大挑战。

针对上述问题，本文提出基于核诱导的不完整多视角聚类算法（kernel-induced incomplete multi-view clustering，KIMV）。首先，有别于传统方法在欧式空间中求解共性视角，本文将在核希尔伯特空间中求解更具表示性的共性矩阵。通过核方法的非线性映射，使得原始线性不可分离的输入映射到新的特征空间中可能会变成可分离的输入[19-20]，即原始线性不可分的数据可以映射进入一个更高维度的空间，它表现出线性模式，可以更容易地表示和提取特征[19-20]。因此当数据投影到核空间后将能提供更多的可鉴别信息，更具描述性。其次，考虑到不同视角提供给模型信息量的差异，而且合理的视角间权重有利于提高聚类的准确性和鲁棒性，因此本文引入香农熵视角加权机制，通过自适应学习视角权重的方式，KIMV能够获得最优的视角权重划分。最后，本文引入图拉普拉斯正则化不仅保持了抗噪性，同时保留局部原始空间内在几何特征，提高了算法的鲁棒性[21]。

本文主要贡献可归纳如下：

（1）与现有方法不同，本文在利用非负矩阵分解技术提取共性矩阵以降低缺失样本影响的同时，引入核方法和核技巧，使求得的共性矩阵更具代表性；

（2）将香农熵自适应视角加权机引入不完整多视角聚类算法，自适应地调整视角间的权重，使KIMV获得最优的视角权重划分，从而提高算法的鲁棒性；

（3）为保证多视角的局部一致性，本文引入了图拉普拉斯正则化，保留了原始空间中的内在几何结构，进一步提高了KIMV 的鲁棒性；

（4）在多个真实多视角数据集上验证了本文方法的有效性，并分析了该方法相对于其他相关方法所具有的优势。

1 相关工作

1.1 核方法和核技巧

本节简要地介绍核方法和核技巧。核方法已成功地应用于输入输出关系不是线性的，类间数据不能被线性边界划分（即线性不可分）的各种学习任务中[21-23]。对于线性不可分的数据，核方法的目标是将其映射到更高的维度，在更高的维度上它们可以显示为线性可分的状态，然后在新的特征表示空间中使用线性模型。令ϕ(x)表示一个样本从原始空间Rn到高维核空间Rp(p≫n)的非线性映射，并且其在核空间的内积可由一个核矩阵表示：

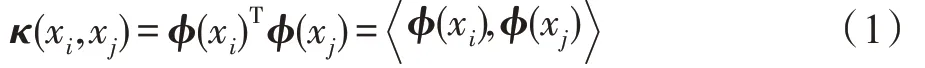
核方法依赖于核函数将原始空间中的数据投影到高维核诱导的特征空间中。常见的核函数包括线性核函数、二次核函数、多项式核函数和高斯核函数。考虑到不同核函数的通用性，本文选择高斯核函数作为核函数，其可表示如下：

其中，σ表示高斯核的带宽。

1.2 不完整多视角聚类

假设给定一个数据集{Xv,v=1,2,…,V}，包括N个样本，C个类别，V个视角，其中X∈RN×dv表示第v个视角的数据。给不完整聚类问题定义一个标识如下：

其中，Mv=[mv,1,mv,2,…,mv,n]T的每一行都是对应视角的样本表示。大多数多视角聚类算法假设所有视角都是完整的，每个视角包含所有样本，即v=1,2,…,V。然而在多数真实场景中，某些样本可能只出现在某些视角中，这可能导致某些视角不完整。如果第v个视角的数据Xv将有一定数量的行数缺失，那么不完整多视角聚类算法的目标就是通过集成所有的不完整视角，将所有N个实例划分到C个簇或类中。

为解决不完整多视角聚类问题，目前已提出不少有效方法，Li 等人利用NMF 学习对齐空间的共性矩阵和非对齐空间的私有共性矩阵提出了PVC[11]，但是该方法只能处理两个视角的不完整数据，并且仅使用L1正则化进行约束，忽视了数据的内在结构。Zhao 等人将流型正则化融入PVC，提出了IMG[12]，该方法利用数据内在结构提高了聚类效果。为解决已有方法只能处理两个视角的不足，Shao 等人使用加权非负矩阵分解技术和L2,1正则化项提出了MIC[14]。已有方法都需要较多正则化来约束，因此不能自适应不同实际数据集，为解决该问题，Wen 等人在PVC的基础上通过将最近邻图应用到矩阵分解的重构误差上提出了IMC_GRMF[16]。然而目前现有方法大都是在欧式空间中求解共性矩阵[11-16,24]，最后对共性矩阵聚类得到最终聚类结果。虽然目前方法已显示出一定有效性，但还存在改进的空间，例如多数数据集在原始特征空间中并不能线性可分，因此找到的共性矩阵不具有较强的代表性，从而导致最终的聚类效果较差。

2 基于核诱导的不完整视角聚类

本章将详细阐述基于核诱导的不完整视角聚类算法。核技巧将被引入非负矩阵分解，并使用图拉普拉斯正规化约束共性矩阵。考虑到不同视角对于聚类的贡献不一致，进一步还引入香农熵自适应视角加权机制。具体细节描述如下。

2.1 目标函数

对于一组不完整多视角数据{Xv∈RN×Dv,v=1,2,…,V}进行聚类，现有的方法通过对缺失样本进行填充，然后利用非负矩阵分解技术在欧式空间中找到所有视角的潜在的共性矩阵，并最终对最优共性矩阵进行聚类[11-17]。通过引入非负矩阵分解技术，本文的初始目标函数可构造为：

其中，Uv∈RN×c是第v个视角的基础矩阵。H∈RN×c是所有视角的潜在共性矩阵，N是样本个数，c为子空间的维度，根据前人的工作[13-15]，c可定义为数据集的类别个数。

然而在存在缺失数据情况下，欧式空间中数据线性可分性较低或分离并不准确，因此本文利用核方法将原始数据映射到高维空间，使其线性可分，并同时找到更好的共性矩阵，因此式（4）可更新为：

其中，ϕ(Xv)表示第v个视角的数据Xv在核空间中的投影数据。然而在没有明确ϕ(Xv)的情况下，无法求得潜在共性矩阵H和基础矩阵Uv。为解决该问题，前人通过对基础矩阵施加约束[25-27]，使其每个向量都位于ϕ(Xv)的列空间中，即ϕ(xN)WNj，此时Uv可更新为：

其中，Wv中的每一列都满足和为1 的约束条件。将约束（6）引入式（5）中，式（5）可更新为：

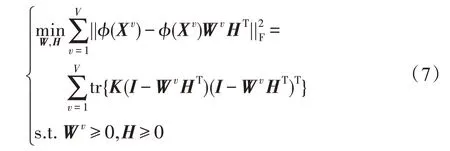
其中，tr{∗}为迹运算，K=ϕ(X)Tϕ(X)为核矩阵，I为单位矩阵。

为减少缺失视角带来噪声的影响，现有的方法[11,13-14]通过添加L1,L2正则化来提高模型的鲁棒性。然而前人的工作[21]表明，保持局部结构不仅能够提高抗噪能力，还能提高聚类质量。传统L1,L2正则化忽视了每个视角数据内在几何结构，为弥补此不足，本文进一步引入图拉普拉斯正则化惩戒项[28]，此时式（7）更新为：

其中，β为惩戒参数，Dist(κKv,κH)为图拉普拉斯惩戒项，本文利用如下方式构造：针对核空间中每个视角的数据Kv构造一个具有N个顶点的最近邻图Gv，该最近邻图视为视角v的局部流行结构模型。构造相似性矩阵Sv，若在特征空间中样本为样本的k近邻点（本文中k设定为5），则为核函数，否则。构造其中为使两个在核空间中足够近的点映射到共性矩阵后能够保持原有拓扑结构，本文定义如下函数[21]：

其中，Lv=Dv-Sv为拉普拉斯矩阵。结合式（9），式（8）更新为：

在多视角数据场景下，不同视角常常具有不同的物理意义和判别能力，特别是在不完整多视角场景下，由于多视角可用样本的特征维度和数量不同，不同视角的可用判别信息会有很大的差异。因此引入视角加权机制来调整各视角的影响有极大意义。为此，本文引入香农熵自适应视角加权机制来自动学习各个视角的权重，以平衡不同视角的重要性[29-30]。此时式（10）更新为：

其中，av表示第v个视角的权重，λ为香农熵的正则化参数，为负香农熵正则化项。通过引入负熵技术，使目标函数达到最优时负熵尽可能小，负熵极小化会导致各视角权重趋于一致[31]，无法凸显出各个视角的重要性。同时，式（11）的前两项，即式（10）极大化则使得视角权重易于趋向于某一视角，将最具代表性（空间划分最为明显）的视角凸显出来，而该视角将控制最后的聚类结果。上述两种情况为极端情况，本文对它们进行了平衡，以获得更好聚类结果。本文在各个视角上引入自适应熵加权的概念，该方法能够有效降低聚类特性较差视角的干扰和一个视角控制输出的风险，从而获得更为理想的空间划分结果，最终增强本文算法的有效性和鲁棒性。

2.2 优化

为了求解式（11），本文采用经典的交叉迭代策略，迭代过程包括三个主要步骤，即对Wv、H、av分别进行迭代更新。

（1）更新Wv

当H和av固定为常数时，需要最小化如下目标函数：

通过将式（12）相对于Wv的导数置于零，并利用KKT（Karush-Kuhn-Tucker）[32]互补条件，由此可得到Wv的更新公式：

（2）更新H

当Wv和av固定为常数时，需要最小化如下目标函数：

通过将式（14）相对于H的导数置于0 并利用KKT 互补条件，由此可得到H的更新公式：

（3）更新av

当Wv和H固定为常数时，需要最小化如下目标函数：

通过将式（16）相对于av的导数置于0，由此可得到av的更新公式：

通过对式（13）、式（15）、式（17）交替迭代优化，可以得到目标函数的最优解，在最优的共性矩阵H基础上，利用K-means聚类算法得到最终聚类解。

基于上述推导和分析，算法1 给出KIMV 的细节描述。

2.3 算法描述和分析

本节将分析KIMV 的计算复杂度。算法KIMV的复杂度主要由在更新过程中矩阵乘法的矩阵逆运算决定。在每次迭代更新中，更新av的计算复杂度为O((N2C)2N2VT)，N为样本数，C为类别数，V为视角数，T为迭代次数。更新Wv的计算复杂度为O((N2C)2NCVT)。更新H的计算复杂度为O((N2C)2(NCN+1)T)。因此，KIMV算法的总计算复杂度为O((N2C)2(NCN+1)T)。

2.4 与相关方法的联系与区别

虽然本文提出的KIMV与现有的方法，如PVC[11]、IMG[12]、MIC[14]、IMC_GRMF[16]等一样都基于非负矩阵分解技术求解共性矩阵，然后进行聚类操作，但不同的是KIMV 将求解空间映射到核希尔伯特空间中，相比在原始特征空间求解到的共性矩阵更具代表性。并且值得注意的是：（1）之前的方法并没有注意到不同视角的贡献程度不一致，而KIMV 利用香农熵实现视角的自适应加权获得了最优的视角权重分配。（2）虽然MIC 和PVC 中使用的L2,1和L2正则化能够很好地提高模型的抗噪性，但同时忽略了数据的内部几何结构。而KIMV 和IMG 利用图拉普拉斯正则化兼顾这两点，大大提高了模型的鲁棒性。

3 实验结果和分析

本章对提出的不完整多视角聚类（KIMV）进行实验研究。

3.1 数据集

本文所用多视角数据集均来自UCI 数据集库。表1 给出了数据集的统计信息。其中，IRIS 数据集本身并非多视角数据集，其特征人为地划分为多视角数据，下面给出数据集的详细描述。

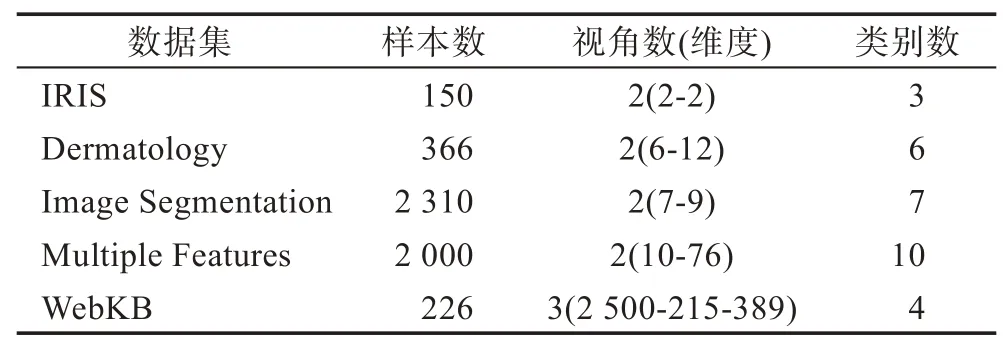
Table 1 Statistics of datasets表1 数据集的统计信息

（1）IRIS 数据集：IRIS 数据是UCI 数据库中的经典数据集，本文将其每两维特征看成一个视角，即，将原来的IRIS 数据集拆分成两个视角样本集合。

（2）Dermatology 数据集：该数据集用于判定红斑鳞状皮肤病的类型，共有两个视角，包括组织病理学视角和临床视角。

（3）Image Segmentation 数据集：采用的图像分割数据集由从7 个室外图像的数据库中随机抽取的2 310 个对象组成。该数据集包含19 个特征，可以自然地分为两个视角，形状视角和RGB 视角。

（4）Multiple Features 数据集：UCI 数据库经典手写字数据集，总共包含5 个视角，本文选取其中两个视角，即傅里叶系数视角和Zernike矩阵视角。

（5）WebKB 数据集：WebKB 数据集在多视角学习的研究中被频繁使用。该数据集收集了4 所大学的网页，共1 051 页。可分为网页文本视角、网页超链接视角和标题文本视角。在本文实验中选取其中一个大学的网页作为数据集。

3.2 实验设置

在实验中，KIMV 将和如下的多视角聚类算法进行比较。

（1）MultiNMF[7]：MultiNMF 作为基于非负矩阵分解技术的传统多视角聚类算法无法直接处理不完整的多视角数据，因此在实验中，先使用平均特征值填充每个不完整视图中的缺失实例。

（2）PVC[11]：PVC通过学习对齐实例的公共子空间和未对齐实例的私有子空间进行不完整多视角聚类。

（3）IMG[12]：IMG 融合了PVC 和流型学习，通过学习完整的图拉普拉斯正则化项，将不同视角缺失的实例数据连接起来。

（4）MIC[14]：MIC 利用加权非负矩阵分解技术和L2,1正则化对多个不完整视角进行聚类。

（5）OMVC[15]：在线不完整多视角聚类算法是MIC 的改进版，大大减少了MIC 算法运算的时间和复杂度。

（6）IMC_GRMF[16]：IMC_GRMF 在矩阵分解的重构误差上加入最近邻图，利用数据的局部几何结构，使算法能够学习的共性矩阵更有鉴别性。

为了公平起见，在实验中所有算法的正则化参数都将设置在{10-3,10-2,…,103}内，KIMV 的核宽设置在lg{0.01,0.05,0.10,0.50,e,e2} 内。实验评判标准本文跟随文献[33]，选用归一化互信息（NMI）、准确度（Acc）和Purity 作为评价指标。与文献[14]相似，对于完整的多视角数据集，将随机移除每个视角一定比例的样本，移除的比例将从10%到50%依次递增，并且对于每个数据集，所有的方法都是在相同的5 个随机形成的不完全比例上执行，并以它们的平均结果作为最终结果进行比较。需要注意的是PVC、IMG 和IMC_GRMF 这3 个算法只针对两个视角的数据，因此它们在WebKB 上没有结果。

3.3 实验结果和分析

本文算法与其他6 个不完整多视角聚类算法在4个数据集上的实验结果如图1 所示，表2 列出了4个算法在3个视角数据集WebKB上的详细结果。

Fig.1 Clustering performance of each algorithm on 4 datasets图1 各算法在4 个数据集上的聚类表现

通过观察图1和表2可以得到如下结论：（1）KIMV在多数数据集上与其他算法相比具有显著优势，因此本文算法具有较好的性能。（2）MultiNMF 与其他算法相比，性能较差，这表明存在缺失样本情况下传统多视角聚类算法不再可靠。（3）KIMV、IMG 和IMC_GRMF 在大多数情况下表现优于PVC，这证明利用图拉普拉斯正则化保留数据内在几何结构，有利于提升算法性能。（4）在多数情况下，特别是当缺失视角较多时，KIMV 与其他算法相比，在Acc、NMI和Purity 上都有较大优势，这说明不仅在核空间中求解的共性矩阵能够提供更多聚类信息，并且考虑不同视角的重要性，能够大大提升聚类效果。

Table 2 NMI,Acc and Purity of 4 methods on WebKB表2 4 个算法在WebKB 上的NMI、Acc、Purity

3.4 有效性分析

为研究拉普拉斯正则化和自适应视角加权机制是否给模型带来正面影响，本节在含有20%缺失数据情况下分别移除拉普拉斯正则化项（KIMV1）和自适应视角加权项（KIMV2）进行实验，表3 给出3 种情况下的NMI结果。通过观察表3 可以看出，通过利用自适应视角加权项和拉普拉斯正则化项可以较大提高模型的鲁棒性，此外在多数数据集上拉普拉斯正则化的作用要大于自适应视角加权项。

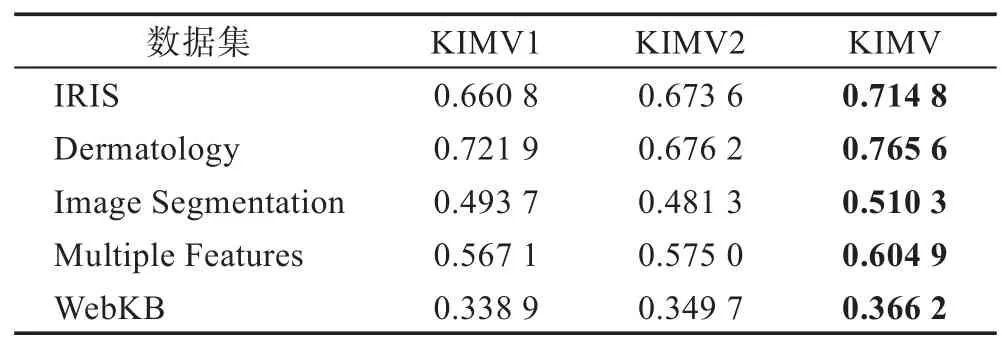
Table 3 NMI of 3 KIMV on 5 datasets表3 3 种KIMV 在5 个数据集上的NMI

3.5 参数分析

参数β用于控制拉普拉斯正则化项的影响，一个好的惩戒参数设置会对模型性能的提升有较大影响。因此为研究参数β对KIMV 的影响，在本节实验中，将另一个作用较小的参数λ固定，然后利用网格搜索的方法观察参数β采取不同值对算法效果的影响。考虑到缺失样本过少，不具有代表性，而缺失样本过多时不能体现算法的特点，本文在5 个数据集中以含有20%缺失数据情况为例进行参数分析，实验结果如图2 所示。

由图2 可得出如下结论：5 个数据集对于β的敏感程度较为一致。当参数β较小时算法性能较好，而当β逐渐增大，算法性能开始下降。可以看出β在{10-3,10-2,10-1,100}区间内算法取得较好性能。

3.6 收敛性分析

Fig.2 Sensitivity analysis of parameter β on 5 datasets图2 参数β 在5 个数据集上的敏感度分析

本节通过实验证明了所提算法的收敛性，同样以20%不完整率情况为例。受文章篇幅限制，只给出Dermatology 和Multiple Features 两个多视角数据集上的实验结果。图3 和图4 分别为Dermatology 和Multiple Features 数据集的收敛曲线和性能曲线，其中实线为收敛曲线，虚线为性能曲线。可以看出对于Dermatology 数据集，KIMV 迭代到40 次后便收敛，而Multiple Features 数据集KIMV 需要迭代60 次后才收敛。可见KIMV 具有良好的收敛性和稳定性。

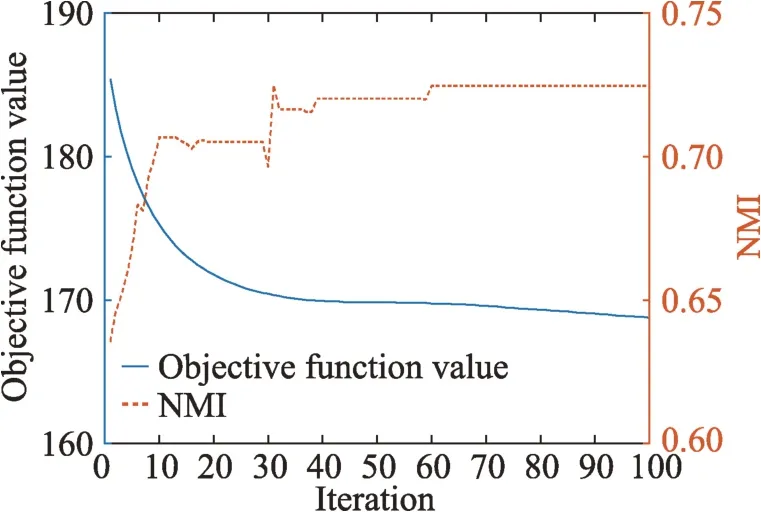
Fig.3 Convergence and performance curve of algorithm on Dermatology图3 Dermatology 上算法的收敛和性能曲线

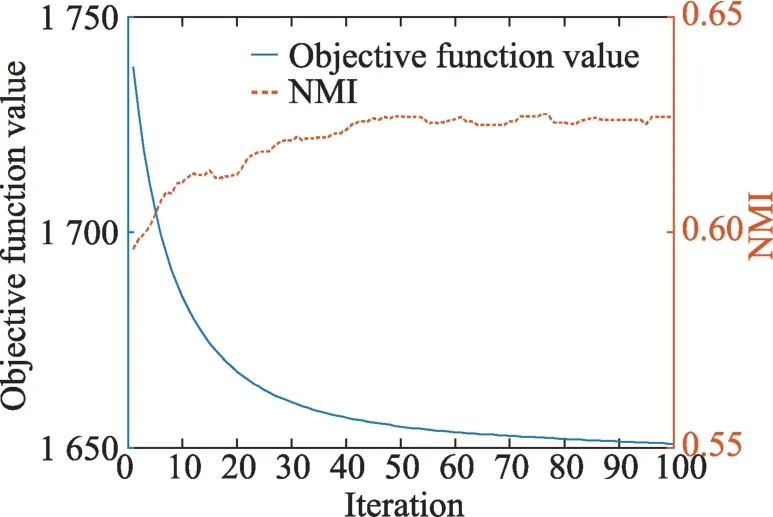
Fig.4 Convergence and performance curve of algorithm on Multiple Features图4 Multiple Features上算法的收敛和性能曲线

4 结论和展望

本文针对多个视角中存在缺省样本时传统多视角聚类算法可靠性大大下降的问题，提出了基于核诱导的不完整多视角聚类算法。该方法利用核方法和非负矩阵分解技术在核空间中对所有视角学习一个共性矩阵，核空间与传统欧式空间相比能提供更多信息，因此学习到的共性矩阵具有更强的表示性，同时样本加权机制能够将缺失样本的负面影响降到最低。另外本文引入图拉普拉斯正则化提高模型对噪声和异常值的鲁棒性。最后本文引入视角自适应加权机制获得了最优的视角权重划分，进一步提高了模型的聚类效果。未来，将考虑提高模型的可解释性，比如将模糊函数引入模型。