实践活动中数学思维的培养策略
薛正桧

培养学生数学思维能力是一个持续、渐进的过程,它不是原始素材的简单堆砌,而是相关要素的逐层递进。教学活动有的放矢,学生的思维才能逐级提升。用三角板画角原本只是“角的认识”课中的一道习题:“你能用三角尺画出15°、150°、165°、75°吗?”这道题在帮助学生加深对三角板认识的同时,可以有效地提升学生的思维能力,教学价值极其丰富。我们将其开发成一节实践活动课,意在为教师寻找培养学生数学思维的路径提供一种参考。
一、从思考到操作
数学是研究数量关系和空间形式的科学,是思维的体操,从内容的表现形式看,通常分三个层次,即形象、表象、抽象。数学最核心、最本质的内容必定是抽象的,它脱离现实,是关于符号的知识体系。但儿童最能理解的数学却是形象的,这和他们的思维水平有很大的关系。教育的目的是培养人,“基于儿童”之后更要“发展儿童”,生活化、儿童化只是学习的桥梁,最终必须数学化。当我们面对问题时,不要急于解决问题,先静下心来想一想,抽象有困难再去结合表象,表象有困难再去结合形象,千万不能一直从低阶开始。实践证明,长期在直观、形象、操作的层面解题,学生的思维就有了惰性,此时再想发展思维能力就更难了。
实践活动“用三角板画角”一课,我们可以按下面的步骤展开教学。1.情境感知:三角板中各有哪几个角?分别多少度?2.提出问题:用三角板可以画出哪些不超过180°的角?3.选择策略:你准备怎么解决这个问题?4.初步设想:你已经想到了哪些角?这些角分别是怎么得到的?5.启发思考:还会有其他不一样的角吗?6.操作验证:请拼出刚才说的这些角。7.思维顿悟:活动中你又发现了哪些不一样的角?8.反思质疑:拼角、画角的过程让你想到了什么?你有哪些收获?在上述教学设计中,操作的作用是验证、巩固,以及思考无助后的灵感触发。这样的课堂,有浓浓的数学味,学生能学到真正的数学。
二、从尝试到联想
从熟知的事物及现象中发现规律,然后通过验证得出结论,是人们获取知识的一般路径。在这条路径下,儿童的观察、猜想、实验、推理、概括等能力得到了有效的训练与提升。小学生喜欢在熟悉的领域内按熟悉的方式进行学习,这是他们这个年龄段应有的状态。从实例中获取知识是一种方式,从已有结论中二次获取知识也是一种方式。数学可以来源于生活现实,也可以来源于数学现实。联想就是一种有效的学习方式。在联想中,学生的思维处于一种发散状态,思维的灵活性、深刻性、敏捷性、创造性等品质都会得到发展。
在“用三角板画角”一课中,我们可以在以下几个方面引导学生展开联想,从熟悉到陌生,有梯度地培养他们的思维能力。第一,运算上的联想。把两个角相加得到新角是学生熟悉的,但把两个角相减得到新角则是学生陌生的。如图1,45°角和30°角合并拼,可以得到75°角,如果将它们部分重叠起来拼,又会得到多少度的角呢?
第二,空间上的联想。在三角板内部拼角是学生熟悉的,但从三角板外部找角则是学生陌生的。如图2,借助一条直线,在两块三角板外,又能得到多少度的角呢?
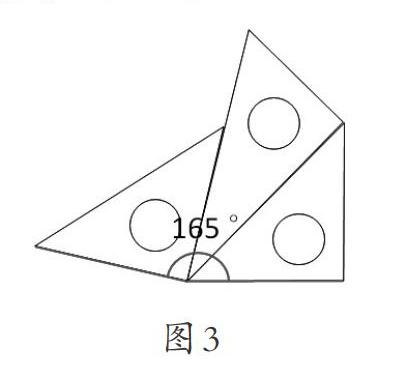
第三,数量上的联想。利用两个角画角是学生熟悉的,但利用三个角或者更多的角画角则是学生陌生的。如图3,在已有75°角(45°+30°)的外延再增加一个90°角,又能得到多少度的角呢?
这样的课堂灵动而富有张力,教师一两句的引导、点拨,便能给学生打开一扇知识的窗口。
三、从零散到系统
有效的学习要体现在对某个知识点的理解与掌握上,也要体现在对既有认知系统的扩充或重组上。零散的知识点只有经过系统化后,才能内化为学生的所得。一方面,零散的知识记忆起来麻烦,而且很容易忘记;另一方面,零散的知识没有形成体系,容易导致思考問题片面。在教学中,教师要注重沟通新旧知识的联系,注重多角度、多维度地呈现知识,帮助学生把零散的知识组成系统,逐步建立完整的知识结构。在系统化过程中学生的思维更加有条理,这将有利于他们准确地阐述自己的思想和观点,有利于他们运用数学概念、思想和方法,形成良好的思维品质。
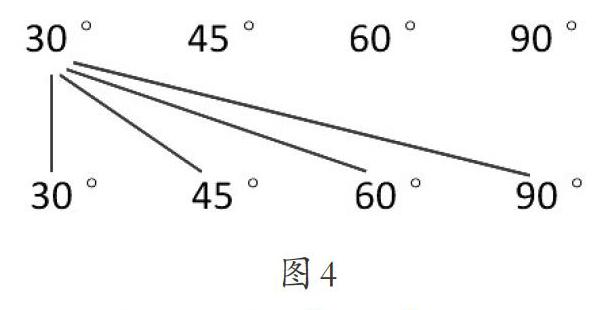
在“用三角板画角”一课中,我们至少可以从以下两个方面引导学生对零散知识进行系统化整合。一是与“搭配(排列组合)”连接。用三角板画角,换个思路看,其实就是对三角板中已有的角度(30°、45°、60°、90°)进行自由组合。按图4的方式,先两两连线得到16种组合,再分别进行加减运算得出32个度数,最后剔除相同的答案。在此基础上,为了得到更多的角度,还可以将刚刚得到的度数再与原有的4个度数组合。
二是与“找规律(等差数列)”连接。在学生尝试以后,可以让他们将初步得出的角按顺序排列起来(15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、165°、180°)。此时学生得出的角可能不全,这很正常,不用刻意补充。教师只须引导他们观察已有数据,努力发现数值排列的规律。因为有丰富的找规律经验,他们会很快发现相邻两个角之间的度数差大部分是15°或全部是15°。之后,找全的学生会根据“等差”这一特性进行更全面的思考;找不全的学生会自觉补全遗漏度数,并进行尝试、验证,最后获得完整答案。我们还可以从15°的整倍数这个角度引导学生发现、归纳,构建出多维的知识体系。零散的度数有了系统化的理解后,学生的思维必将深入而持久。
(作者单位:浙江省宁波滨海国际合作学校)

