展平问题“褶皱”，用任务驱动拓展性学习

孙国宏　严育洪

摘 要：数学学习中的许多问题“褶皱”，有的属于学习的苦恼问题，有的属于学习的困惑问题。我们坚持“哪里痛就在哪里学”“哪里痒就在哪里学”的教学理念，在学生的“痛点”和“痒点”上下功夫、做文章，展平问题“褶皱”，用求助或求解任务驱动拓展性学习，使学生保持自我提升的学习状态，最终提升学习品质。

关键词：问题;任务驱动;拓展性学习

我们曾经看到罗振宇所写的《问题只是褶皱》文章中的一段话：“人生中的绝大部分问题，都像是一块布上的褶皱。那解决它的办法，不是跟这个褶皱的部位较劲，而是把布的其他地方展平，这个褶皱自然也就消失了。……什么是解决问题？不只是聚焦问题本身，而是持续保持一种自我提升的状态，尝试寻找各种自我优化的方法，不管在哪个领域。没准最后发现，褶皱解决了，而且整块布的品质还改良了。”

在数学学习中，许多问题也都像是知识这块布上的褶皱，有的属于学习的苦恼问题，有的属于学习的困惑问题。有时候，解决它们的办法，也不是一味地跟这个褶皱的部位较劲，而是把布的其他地方展平——围绕问题褶皱展开拓展性学习，认识广泛了，理解深刻了，思想通畅了，原有的褶皱自然也就消失了。“不只是聚焦问题本身，而是持续保持一种自我提升的状态，尝试寻找各种自我优化的方法”，如此趁热打铁、借题发挥的做法或许能够达到“褶皱解决了，而且整个学习的品质还改良了”这种一举两得的学习效果。

一、展平学生的苦恼问题，用求助任务驱动拓展性学习

在任务驱动学习中，我们倡导“哪里痛就在哪里学”的教学设计理念，因为学生学习的“痛点”正是开展新知识学习以及拓展性学习的大好时机。科幻作家郝景芳在《孩子觉得学习枯燥，是因为这一点没做对》一文中写道：

我们这么多年的学习，都是“只给钥匙，不给锁”的学习。顺序一般是：讲述一个概念→给出定义公式→熟悉应用场景→反复练习使用→记住。

这样的学习几乎不会引起学生的兴趣，因为其中没有疑问。没有疑问就没有好奇，没有好奇就没有兴趣。

我们在生活中手指经常会不小心被纸划破，举着划破的手指和纸，就可以问一问学生：“咦，人为什么会被纸划破呢？纸这么软，又不是刀子，怎么手指会被纸划破呢？”学生很可能会惊讶：“不会吧？”进而思考，到底是什么力量划破了皮肤？这时候可以对比刀片和纸，于是可以猜想，也许起关键作用的不是材质，而是纸的锐利，也就是薄。于是进而猜想，当力量非常集中，透过很薄的面传过来，那就可以有很大的杀伤力。

可以说，学生学习的“痛点”正是那把“锁”，它能很好地将学生所有的心思锁到“痛点”的消除上，此刻的学习是学生急切需要的，也必定是高效的。

当然，学习的“痛点”未必是划破手指之痛，更多的是学生遭遇的“头痛”问题，也就是学习中的苦恼问题。例如，学生学习三角形面积计算公式后，经常会忘记“÷2”，这让学生“头痛”，而许多教师的解决办法也就是“跟这个褶皱的部位较劲”，让学生反复记公式。然而，我们都知道，死记硬背效率不高，因为一直在重复学习的第一步——输入，而忽视了短期记忆向长期记忆的转化。

一个人学习的过程是这样的：输入新知识→形成短期记忆→大脑对短期记忆进行整理→转化为长期记忆。脑科学显示，人脑的长期记忆容量几乎是无限的，只要形成了长期记忆，就几乎不会被忘记。但大脑把短期记忆整理成长期记忆，是个损耗很大的过程，我们学到的新知识，只有不到30%能成为长期记忆，70%以上都会被忘记。

如何减少大脑损耗呢？有一种方法就是让学生产生记住知识的兴趣。如何让学生产生记住知识的兴趣呢？我们就不能一味地“跟这个褶皱的部位较劲”，这样不断重复“昨天故事”的做法只会降低学生的学习兴趣，“因为其中没有疑问”。由此，我们不妨换一种思路，为学生打开另一扇窗，也就是“把布的其他地方展平”，让学生重新产生疑问，重新产生好奇，重新产生兴趣，在拓展性学习的更大知识背景中，引导学生不断丰富对三角形面积计算公式中“÷2”这一关键点的认知，在深刻理解知识的基础上形成长期记忆。

所以，我们应该摒弃原来小打小闹甚至死缠烂打的简单做法，把传统学习新知识后以解题为知识目标的练习课，变成现在以解决苦恼问题为任务目标的“恋习课”。称其为“恋习”，是因为由学习“痛点”引发任务：怎样牢牢地记住“÷2”？学生有着强烈的需要。这样的“恋习课”，不只是聚焦问题本身，还着力通过把问题展平——尝试寻找更多可以帮助理解的方法，来实现知识的不断拓展和认知的不断优化，最终在解决问题的同时，学生的学习品质得到改良，也就是一切的解题都是为了解决困扰问题，用学生需要的任务驱动的练习课自然多了一份情感力量，很容易进化成受到學生普遍支持的“恋习课”。具体设计如下。

第一次拓展：材料由2个到1个。

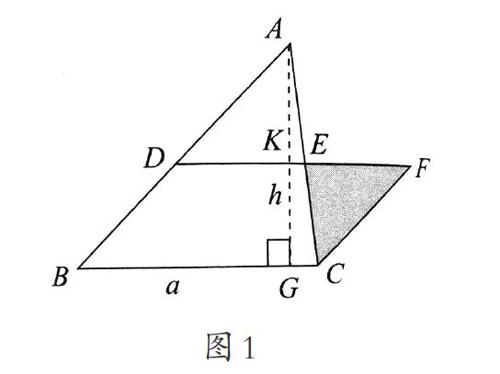
三角形面积计算公式“S=ah÷2”，我们可以有3种不同角度的解读：一是看成“S=（a×h）÷2”，也就是教材编排的用两个完全一样的三角形拼成平行四边形来推导三角形面积计算公式的思路;二是看成“S=a×（h÷2）”，这是用图1的方法推导三角形面积计算公式的思路;三是看成“S=（a÷2）×h”，这是用图2的方法推导三角形面积计算公式的思路。

在这节拓展课上，我们紧扣学生按照教材编排进行三角形面积公式推导时产生的疑问——“为什么不像前面学习平行四边形面积公式推导那样，只用一个三角形来探究？”抛出拓展性任务：“你能只用一个三角形推导出三角形面积计算公式吗？”学生在好奇中产生一探究竟的兴趣，最终得到“S=a×（h÷2）”和“S=（a÷2）×h”两种思路，强化了与教材编排的推导方法“S=（a×h）÷2”的比较，拓展了学生对“÷2”的理解，加深了学生对“÷2”的印象，也消除了学生原有的疑惑。

第二次拓展：结果由1种到多种。

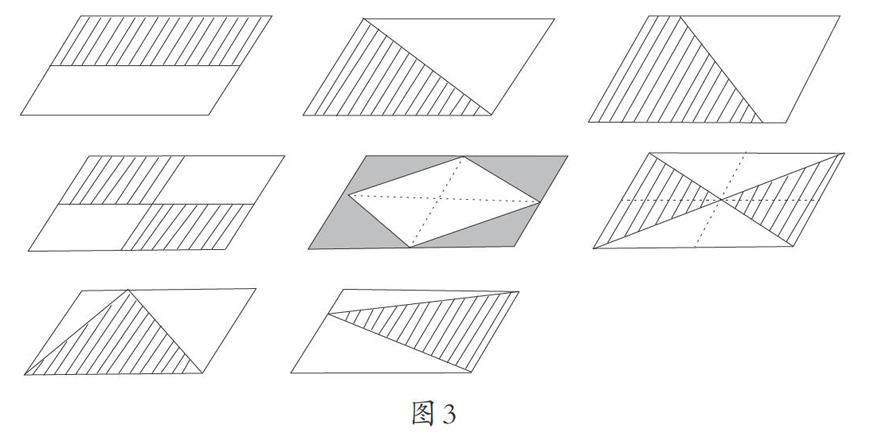
在上述组织学生研究“把谁除以2”的基础上，我们转换视角进一步拓展，组织学生研究“ah÷2还可以是谁的面积”，抛出拓展性任务“你会用阴影表示出平行四边形的一半吗”，也就是“（ ）= ah÷2”，拓展了学生对“ah÷2”结果多样性的认识（如图3），开阔了学生的思维，也练习了以后才学的求阴影部分面积的方法。其中，虽然不再盯着三角形，却始终盯着“÷2”，强化了学生对“÷2”的印象。

第三次拓展：分法由“÷2”到“÷3”。

除了改变“÷2”所指向的对象和“÷2”所得到的结果，在分法上我们还从“÷2”拓展到“÷3”，出示挑战性任务：“如图4，阴影部分可以用[1/3]表示吗？”

认为可以用[1/3]表示的学生想到的证明方法如图5所示，让我们看到上述推导三角形面积计算公式所使用方法的影子。从表面看，这一习题并没有直接指向“÷2”，但它们解决问题的方法一样，再次加深了学生对“÷2”的印象。

二、展平学生的困惑问题，用求解任务驱动拓展性学习

在一次讲座上，有学生问校长：“什么叫学生？”校长答：“学生就是学‘生。第一，要学生活的常识;第二，要学生存的技能;第三，要学生命的意义和价值。”确实，教学不仅让学生学陌生的知识，我们还应该通过拓展性学习让学生看到知识的用处，获得更多的感悟，学到更多的本领。

例如，在“圆的认识”一课中，学生对教师引用诗人但丁“圆是最美的图形”这句名言深感兴趣，也深感困惑：“为什么说‘圆是最美的图形？”在用任务驱动学习中，除了倡导“哪里痛就在哪里学”以外，我们还倡导“哪里痒就在哪里学”的教学设计理念，只要学生心里感到痒痒，有探求真相的念头，哪怕只是一念之间，哪怕对知识的继续学习无关紧要，我们也会趁热打铁，以此为探究性任务，驱动学生进行拓展性学习。

第一次拓展：走进生活圈认识“圆是最美的图形”。

在西方数学史、哲学史上有一种说法：“上帝是按照数学原则创造这个世界的。”我们利用教材（苏教版六年级上册）的“你知道吗”内容的上半部分图片（如图6），通过欣赏自然现象中大量的圆形事物，让学生体会圆形的美。

生活中也大量应用圆形设计，除了几何学原理（“圆的认识”数学课的知识教学）以外，还涉及材料与工程学（节省材料并使其结实）、美学（好看）、人体工程学（使人方便使用）、空间学（装最多的东西及节省存放空间）、力学（圆柱侧面受力最均匀，力的构造最稳定）等拓展性知识，让学生体会到圆形是具有最多优点的一种形状。

接着，我们还拓展到心理学，介绍了生活中“人更喜欢圆形物体”的心理学原理，圆形代表善良，喜爱圆形的人善良纯真。在视觉实验中，相较其他形状的图形，婴儿凝视圆形图案的时间最长。因此，每个人对圆形事物始终寄托着美好的感情。

第二次拓展：走进文艺圈认识“圆是最美的图形”。

我们利用教材（苏教版六年级上册）编排的“你知道吗”内容的下半部分图片（如图7），通过欣赏艺术领域中大量存在的圆形事物，让学生体会到圆形的美。

我们还把圆规与人的图片放在一起（如图8），学生对圆规的形状与人的优美姿态、圆规的操作与人的优美运动产生拓展性联想，进入美好的意境体验。

我们还乘机配上一幅漫画（如图9），圆规的转动成了圆规的“跳舞”，学生以后使用圆规画圆的时候，就可能会产生如此美好的联想并获得如此美好的体验，让圆规的使用变成一件快乐的事情。

我们还组织学生阅读爱默生的散文《圆》：

眼睛是第一个圆，眼前的地平线是第二个圆。这个原始的形状在自然界到处都是，没有止境。圆是一种最高形式的象征。它有着无所不在的圆心，但是其圆周却无处寻觅。我们用一生的时间来研究这个最原始的图形有什么丰富内涵。

在讨论人类每一个行为的循环及其补偿性时，我们从中探寻出了一种道德寓意。有这样一条真理贯穿在我们的生活当中：在任何一个圆的外围都可以画出另外一个圆;自然没有极限，每个终点都是一个新的起点。

虽然文学中的“圆”比较模糊，但学生一点儿都不迷糊，阅读中会时不时地浮现或描绘圆的形象——“眼睛是第一个圆，眼前的地平线是第二个圆”“在任何一个圆的外围都可以画出另外一个圆”，它也考查着学生对圆的认识——“我们用一生的时间来研究这个最原始的图形有什么丰富内涵”。其中，对圆的认识首先考查的是数学中的“圆的认识”，然后才是站在生活、生命等更高层面对“圆是一种最高形式的象征”的理解。此时，学生对“圆是最美的图形”就有了更深刻的体会。

我们组织学生开展了以“圆的认识”为主题的创作任务活动，例如：“圆内代表已知世界，圆外代表未知世界，未知世界永远大于已知世界。”“圆没有起点，也没有终点，人生也是如此。生生死死，如此轮回，没有起点，也没有终点。”……随着对圆的认识的不断深入，学生也就能够慢慢理解古希腊哲学家芝诺对学生所说的一段话：“人的知识就像一个圆，圆圈外是未知的，圆圈內是已知的，你知道的越多，你的圆圈就会越大，圆的周长也就越大，于是，你与未知接触的空间也就越多。因此，虽然我知道的比你们多，但不知道的东西也比你们多。”此时的“圆的认识”反映出来的不仅是数学上的认识，还是拓展到思想上的认识。学生学到的不仅是陌生的知识，还是生活的常识、生存的技能，更是生命的意义和价值。

这一次拓展性学习的“长征”之路，始于学生对但丁一句名言的不解，虽然这样的困惑对数学成绩没有影响，只是学习过程中的问题“褶皱”，但我们看到了进行拓展性学习的大好机会，“不只是聚焦问题本身”，而是由此出发，不断向外荡起一圈又一圈的涟漪，让学生看到更多、更高、更美的知识风景，最终提升学习品质。

（作者单位：江苏省无锡市蠡湖中心小学   江苏省无锡市锡山区教师发展中心）

参考文献

[1]管国贤，严育洪. 任务驱动式教学在小学数学教学中的应用[J].江苏教育研究，2012（8）.

[2]严育洪.课堂的突围与开放[M].福州：福建教育出版社，2013.

[3]严育洪.让学习真正发生——小学数学任务驱动式教学解读与实施[M].济南：山东文艺出版社，2017.

投稿邮箱：405956706@qq.com

作者简介

孙国宏，江苏省无锡市蠡湖中心小学校长，无锡市小学数学教学能手。曾被评为江苏省无锡市优秀教育工作者、陕西省延安市优秀教师。多篇论文在省级期刊上发表。