从问题开始,让学习走向深入
施娅林

英国科学家培根曾说过:“如果你从肯定开始,必将以问题告终;如果从问题开始,则将以肯定结束。”对学生而言,单单获得一个结论,并不意味着他们掌握了知识。真正有效的学习过程,是培养发现并解决问题的能力。于是,笔者对“3的倍数特征”再思考,试着从关注儿童问题的角度思考这节课。
一、初教学:触于“表”难及“里”引发的问题
在苏教版五年级下册“3的倍数特征”这一课中,教材给学生提供了多种探究素材,如百数表(图略),先找到相应的3的倍数,再通过观察从个位上看不出3的倍数特征,引导学生猜测并验证自己的猜想,从而总结出3的倍数特征。
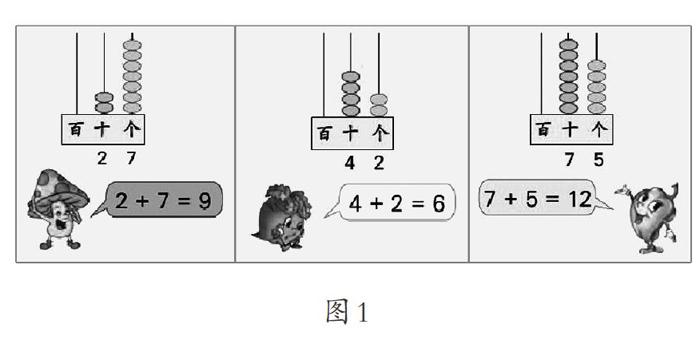
再如计数器(图1):先拨出3的倍数,再数出所用算珠总数,以此抽象出各个数位上数字和的特点。
由于部分学生课前已有知识基础,很快就记住了3的倍数特征。这时候,有个学生突然问道:“为什么一个数各位上数的和是3的倍数,这个数就是3的倍数啊?”
课后,笔者思考:当新知与之前学习2和5的倍数特征不一致的情况下,学生会出现思维的“盲点”,他们很难通过“根据一个数的各位上数的和是否是3的倍数”来进行判断,而且并不理解3的倍数特征为什么是各位上数的和是3的倍数。那么,有没有必要回到思维的原点,从数学本质的角度来回答那个学生的问题呢?特级教师贲友林在《贲友林与学为中心数学课堂》这本书中提出:对数学内容的理解,有“工具性理解”与“关系性理解”两种模式。“工具性理解”是对数学对象的表层理解,只知道做什么,不知道为什么这样做;而“关系性理解”是对数学本质的把握,“不仅知道要做什么,而且知道理由”。因此,数学研究只知道“是什么”是不够的,我们要沿着教材脉络大胆地进行再探究。
二、再出发:研究问题,由浅入深,触及本质
师:我们今天就来探究“为什么一个数各位上数的和是3的倍数,这个数就是3的倍数”这个问题,选择你喜欢的方式来进行研究。
(学生自主探究后汇报)
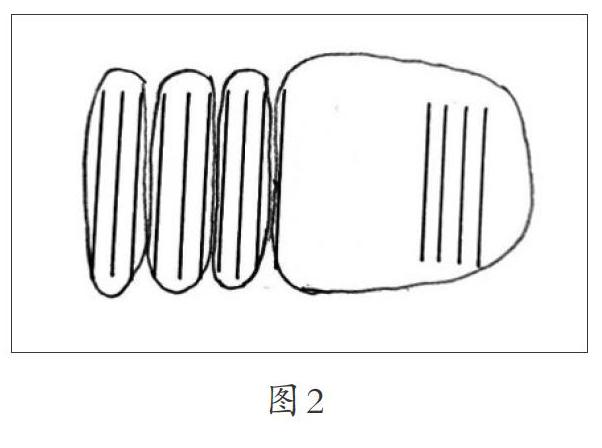
生:我是通过画小棒图来研究的,如图2,画了14根小棒,一捆是10根,拆开3根3根地分,还会剩下1根,这剩下的1根和其余的4根合在一起,可以看成1加4等于5,5不是3的倍数,所以14不是3的倍数。
生:如果是24根小棒,也是同样的道理(如图3),可知24是3的倍数。
生:用字母a,b,c表示出了一个三位数(如图4),百位上的a表示a个百,十位上的b表示b个十,个位上的c表示c个一,把这个三位数拆分就可以写成100a+10b+c。99和9是3的倍数,100a分成99a+a,10b分成9b+b, 99a和9b肯定是3的倍数,只要看a+b+c是不是3的倍数就行了。
师:今天研究的是3的倍数特征,用这样的方法还能找到其他数的倍数特征吗?比如说4的倍数特征。
……
原本只是解决那个学生提出的问题,结果衍生出了后续这么多的精彩问题。所以,问题不是壁垒,更不是终点。相反,问题是内驱,是动力,也是研究的方向,问题终将引领我们走进更美好的数学课堂。
三、再思考:從学生的问题开始,让学习走向深入
关注学生的问题,其实就是为学生深入学习知识本质提供了契机。那么,在教学时如何应对学生的问题?
1.重视学生的问题,顺问引导。笔者在初次教学时忽视了学生的问题,以浅显的发现和个别学生的答案代替了学生对知识的理解。其实大部分学生对“3的倍数特征”这一知识并不理解,只是简单套用公式,这不利于学生的思维发展。于是,在经过思考后,笔者重新出发,重视学生的问题,对学生进行引导,由浅入深,触及本质。理解并掌握了“3的倍数特征”后,引发学生思考“4的倍数特征”“6的倍数特征”等问题。这样教师的引导会让问题更丰富,让数学课堂更丰实。
2.深入研究学生的问题, 顺问学习。在上述再出发的教学过程中,围绕着学生的问题“为什么一个数是否是3的倍数要看这个数各位上数的和”展开深入研究,充分让学生在做中学,在学中思,在思中辨。我们也看到学生由直观的举例,自然地过渡到抽象的字母表达式,体现了从特殊到一般的数学思想。“3的倍数特征”这个概念确实比较抽象,学生难以理解,如果借助直观的画图、举例、对数的拆分,触及知识背后的本质,学生就能真正理解与掌握知识。
(作者单位:南京外国语学校河西初级中学第一附属小学)
投稿邮箱:405956706@qq.com

