PME算法在神威太湖之光上的移植和优化
林 增,武 铮,安 虹,陈俊仕
(中国科学技术大学 计算机科学与技术学院,合肥 230026)
1 引 言
分子动力学模拟(molecular dynamics,MD)是通过数值求解牛顿运动方程获得分子、原子运动轨迹的计算机模拟方法,广泛应用于物理、化学和生物体系的理论研究.由于目前分子动力学可模拟的时间尺度在ns量级,远不能满足真实实验的需求,所以在超级计算机上对分子动力学模拟应用进行移植优化有了更迫切的需求[1].现有很多分子动力学模拟软件普及于各个研究领域,例如NAMD[2]、LAMMPS[3]、AMBER[4]等.其中大部分MD应用支持不同平台上进行模拟,例如CPU、GPU、FPGA等.
GROMACS是广泛用于MD模拟的开源软件包之一,主要用来模拟蛋白质、脂质、核酸等生物分子的运动,以推测物质的宏观特性[5].GROMACS计算非键相互作用的效率很高,使得越来越多的研究小组使用它来模拟非生物体系.同时,GROMACS是免费的开源软件,现由世界各地的大学和研究机构共同维护.
MD应用的热点在于非键力计算部分[6],为了优化计算模式,GROMACS进一步根据原子的截断半径大小将非键力分为短程力和长程力两部分.对于短程力,粒子只需要计算自身和截断半径内的原子相互作用;而对于长程力,粒子需要计算自身和体系中其他粒子的相互作用,GROMACS内部采用PME(Particle Mesh Ewald)算法将时间复杂度降低为O(NlogN)[7].最初短程力作用是程序热点,GROMACS官方代码早期在通用平台上对其进行优化[8,9]之后,热点转移到长程力作用,所以GROMACS最新官方代码在通用平台进一步优化PME算法.同样,已有研究团队基于申威平台对短程力作用开展研究[10,11],在短程力作用优化之后,申威平台上的PME算法占比75.3%,成为了程序热点.因此,本文通过重构PME计算代码,完成PME算法在神威太湖之光上的移植和优化.
神威太湖之光是世界排名第3的超级计算机,其性能主要来自于SW26010众核处理器芯片[12].如图1所示,每个SW26010包含4个核组(core groups,CGs),核组之间通过片上网络(network-on-chip,NoC)连接.每个核组由一个运算控制核心和一个运算核心阵列组成,主核(management processing element,MPE)主要负责管理和通信等逻辑复杂部分,运算核心阵列是由64个从核(computing processing element,CPE)通过8*8网络互连,主要负责计算密集部分.内存层次上,主核包含8G DDR3内存,32KB L1指令cache,32KB L1数据cache和256 KB L2指令数据cache;相比之下,每个从核只包含16KB L1指令cache和64KB的局存(local directive memory,LDM),其中局存为每个从核所私有.计算能力上,主核和从核的时钟频率都为1.45GHZ,且都使用256位向量指令.由于主从核工作频率相同且单芯片内的从核核心数远大于主核,所以从核贡献了整个芯片97%的浮点性能.数据传输上,从核可以通过DMA高效地获取主核内存中连续区域的数据,否则只能通过高延迟的全局加载/存储指令(gld/gst)来访问主核内存中的数据.

图1 SW26010芯片架构Fig.1 SW26010 architecture
实际上,将PME算法移植到神威太湖之光还存在很多困难.一方面,SW26010存在很多限制:从核的局存过小,主从核之间的DMA传输带宽过低等[13].另一方面,PME算法中大量的离散数据访存极大地限制了基于无缓存内存层次结构设计的从核阵列的内存访问效率,以及并行B样条插值[14]引入了网格点写-写冲突为PME算法的优化带来了巨大挑战.为了克服上述问题,本文的主要贡献如下所示:
1)提出基于局部网格序的分块策略,解决了PME算法的并行难点.
2)提出了数据重组策略进一步提升访存局部性,以及使用非线性函数近似等方法提升计算性能.
3)优化后的算法性能相对于初始版本有8.85倍性能提升,相对于CPU向量化版本有1.2倍性能提升.
2 背景介绍
2.1 PME算法
MD模拟需要在短时间内求解N个相互作用粒子的牛顿运动方程,而作用在粒子上的力需要对势能求偏导得到.
(1)
为了消除有限系统的边界效应,一般MD模拟引入周期性边界条件(Periodic Boundary Conditions,PBC)进行处理.在PBC下体系的静电势能可以表示为.
(2)
其中k是关于介电常数ε的量k=1/4πε ,N表示该体系所有的粒子数,q表示粒子的电荷量.在PBC影响下,体系所在的元胞复制出完全相同的元胞(镜像),并向周围空间无限延伸.那么不仅体系中的N个粒子之间会产生静电作用,原元胞粒子与镜像粒子也会产生静电作用.|ri-rj+n|即表示粒子i和跨镜像的粒子j之间的真实距离.式(2)添加*号表示排除两个粒子为同一粒子且同时在原元胞的情况.
由于式(2)属于条件收敛,收敛速度较慢,Ewald加和方法[15]将电势能的求解拆分成如下3部分势能之和,以达到快速收敛的目的.
(3)
(4)
(5)
其中傅里叶空间的结构因子如下所示.
(6)
上述式(3)-式(5)分别表示了实空间(direct space)势能、傅里叶空间(reciprocal space)势能及能量修正项(correction term).erf为高斯误差函数,erfc是erf的互补函数.其中能量修正项的时间复杂度为O(N),不做优化考虑.参数β用于控制实空间和傅里叶空间的计算相对权重,若将β调大,Edir会相对r收敛很快,因此可以采用截断半径的方法将实空间势能的计算复杂度从O(N2)降到O(N).而由于式(6)中的结构因子和难以近似,导致Erec的求解成为瓶颈,使得Ewald加和方法的计算复杂度仍为O(N2).通过引入PME算法,使用基数B样条网格插值方法[16]近似式(6)的值.
(7)
Ml(u2i-k2-n2K2)×Ml(u3i-k3-n3K3)
(8)
其中F(Q)表示Q数组的傅里叶变换,Q表示原体系电荷插值后所得到的三维数组,Ml表示B样条插值系数.那么式(7)、式(8)表示电荷插值到三维网格的散乱数据插值过程,即体系中每个电荷都需要扩散到周围n3个格点上,而对每个格点的电荷贡献由Ml决定.图2为电荷在二维网格的插值过程.
那么最终可以将近似后的傅里叶空间势能代入式(1),得到体系中粒子的受力.

图2 PME电荷扩散示意图Fig.2 Charge spreading in PME
(9)
其中θrec=F(B·C),B、C数组的定义如下.
(10)
2.2 相关工作
近年来,GROMACS作为高性能领域的重要MD应用,已经成为了众多超级计算机的主流应用.众多研究团队在异构计算平台展开研究,并提出了有效的优化方法来提高GROMACS的性能.
Li等[17]通过分析MPI+OpenMP+CUDA的三级混合并行编程模式的性能,实验得出了GROMACS在CPU-GPU集群的最佳配置机制.Wang等[18]在天河二号对GROMACS进行加速,第一次通过offload模式将短程力计算部分offload到MIC卡上,并使用2xnn SIMD代码来加速MIC线程.
Yu等[10]聚焦于在申威平台的芯片级优化,采用软件模拟cache、混合并行计算等方法提高数据局部性,取得了不错的效果.Zhang等[11]聚焦于在神威太湖之光上的系统级优化,通过重构短程力计算代码,RDMA优化通信[19]等方法实现GROMACS在多节点间的优化,取得了较好的性能提升.
Shi等[20]提出使用格点变量收集电荷贡献的策略替代原算法中电荷扩散到格点的方法,通过修改PME算法计算结构从而消除并行时带来的写-写冲突,并将这种方法应用于其课题组开发的GMD程序中.而由于GROMACS代码量巨大,结构体嵌套复杂,模块间联系紧密,无法采用这种方法进行优化.GROMACS最新版本在GPU上移植了PME算法,其直接采用原子加操作消除写冲突,而在申威平台从核不支持浮点原子操作,且从核局存间无法进行共享,使得此方法无法在申威平台进行应用.
上述研究工作是在不同异构平台对GROMACS进行性能优化,但是在申威平台的研究工作只针对于GROMACS中的短程力计算部分,而尚未有将PME算法移植到申威平台的相关研究.并且PME算法在GMD程序及GPU上移植的经验也无法直接利用.在此,本文做了一种新的研究尝试,即设计了一种基于局部网格序的新型分块策略,以此来实现GROMACS的PME算法在SW26010众核处理器上的移植.
3 PME算法在SW26010的移植与优化
首先剖析PME算法在GROMACS的具体执行流程,如图3所示.

图3 PME执行流程图Fig.3 Execution flowchart for PME
大体可以分为如下5个部分:
1)使用B样条值扩散粒子电荷到离散的三维网格,得到式(8)中插值后的数组Q;
2)对网格点执行3D FFT变换;
3)计算傅里叶空间静电势能,并更改网格值;
4)对修改后的网格执行3D逆FFT变换;
5)使用样条值从网格插值得到式(9)中原系统各粒子的受力.
其中电荷扩散是利用FFT变换的前提,是至关重要的过程,且文献[20,21]均提到此过程的并行最具挑战性,也是本文着重优化的部分.除了FFT计算直接调用申威平台的数学库[22],本文也优化了PME算法的其余模块.
3.1 基于局部网格序的分块策略
在模拟系统中,蛋白质本身排列无规则外加PBC的影响,导致空间中电荷几乎是随机分布,当我们直接按原电荷序访问网格点时会严重影响性能.另外电荷扩散需要使用图2所示的B样条插值方法,这种扩散很容易在串行中实现,但在使用细粒度并行时会带来很大挑战,因为当不同的从核尝试在同一网格点累积电荷贡献值时会产生写-写冲突,而SW26010并不支持浮点原子操作.所以我们的移植过程面临上述随机的内存访问模式及写写冲突两大挑战.
为了解决上述问题,本文在每个从核内建立局部网格序以取代原电荷序的访问模式,并建立与原电荷序的映射表.首先将网格空间划分为N块,并对各小网格进行编号(空间标识).考虑到从核架构及局存空间限制,定义划分数N如下.
(11)
其中Ki为原网格各维度大小,order表示B样条插值阶数,上述定义保证了64个从核负载均衡以及充分利用从核局存空间,且每个空间标识对应唯一的从核.然后,为获得核内原子数据的局部网格序,在每个从核内部实现图4所示的局部网格分块算法.
图4使用两个从核来简要解释局部网格分块的并行过程,主要分为4个步骤:
1)将原电荷序排列的原子数据均匀划分到各个从核.
2)从核内部根据原子坐标信息计算所处网格位置,进而计算该网格所在的空间标识,通过界定核内空间标识的种类和数量,获得核内局部空间标识序的原子映射序列.
3)将重排后的局部空间标识序的各从核原子数据整合并更新回主存.
4)借助式(11),各从核收集对应的空间标识的原子数据,例如图4中从核1收集空间标识为Ⅰ的原子序列,从核2收集空间标识为Ⅱ的原子序列.

图4 局部网格分块示意图Fig.4 Local grid partition
至此,通过上述局部网格分块算法,各从核得到了按局部网格序排列的新型原子序列.分块前后的原子序列空间差异如图5所示.

图5 模拟体系空间平面图Fig.5 Simulation system space
图5为模拟体系空间平面图,假定将空间划分成4部分,分别标记为Ⅰ、Ⅱ、Ⅲ和Ⅳ,其中大小不一的圆圈代表有序粒子簇,连线表示跨空间访问,编号代表原电荷序访问次序,灰色的圈标识原子序列访问起始端,跨外边缘连线表示受PBC影响访问镜像粒子簇.图5左图表示分块前沿原电荷序跨空间访问现象严重,导致访问的空间局部性很差,并且电荷扩散过程无法进行并行.而在从核内部利用网格局部性对原子序列重新构建之后,如图5右图所示,粒子簇仅与空间标识块内部的粒子簇连接,且不破坏原来的粒子簇访问次序.每个从核负责一个空间标识块的计算,由于所有的粒子簇都在同一个三维空间,加载到从核局存的网格数据可以被重复使用,很大程度上提高了数据局部性.并且由于各个空间标识下的粒子簇互不冲突,样条插值时所造成的写写冲突也可以通过填充局部网格空间的方式解决,所以从核间可以并行执行.
3.2 数据重组策略
在引入基于局部网格序的分块策略之后,数据访问局部性得到了比较好的改善,但是从核在获取新序列的原子信息时,访问模式仍不连续,如图6左下部分所示.
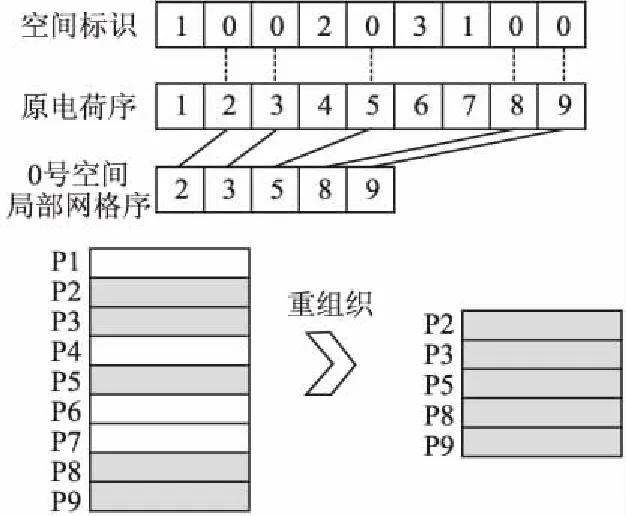
图6 数据重组图Fig.6 Data reorganization
当按0号空间局部网格序访问数据时,由于此时局存中原子信息列表仍按原电荷顺序存储,所以仍需要通过二次索引才能访问粒子数据,导致访问的数据空间不连续.我们将原子列表按局部网格序重组成如图6右下部分所示结构,使得待顺序访问的数据被存储在一个连续的内存区域内.
采用上述数据重组策略,一方面提高了数据的访存连续性,便于进一步实现SIMD并行;另一方面,重组结构丢弃了无用数据,减小了下次数据传输的容量.
3.3 超越函数的优化
在求解静电势能的过程中,同时也需要将式(10)中B、C数组与网格值相乘,为库仑力的插值求解做准备.而计算C数组时,引入了exp超越函数.最初的从核移植版本直接调用神威内置数学库函数,其中内置的超越函数来自GNU的libm库实现,需要调用查找表.由于查找表的大小一般会大于从核局存大小,所以将查找表放置在DDR3主存上进行访问,而这高延迟的数据传输导致了超越函数性能低下.求解静电势能部分是计算密集型的模块,而内置exp函数占了91%的计算时间,成为该模块热点.因此本文设计了基于多项式的方法[23]来近似求解超越函数.
由于单纯使用多项式近似无法在全局定义域上高精度近似exp函数,所以我们将exp函数拆分成两部分,如式(12)所示.左半部分乘数较大,主要是扩展exp函数的定义域,可以通过设置浮点数的指数部分实现.右半部分乘数较小,主要是为保证exp函数的精度,采用式(13)的多项式近似实现,此多项式在近零区域的精确度较高.
ex=ep·ln2+q=2p·eq0 (12) (13) 最终我们的近似方法有10.2倍的性能提升且可以非常好地拟合任意值的指数函数,双精度和单精度的近似误差分别为3.5×10-12和1.2×10-7,充分保证程序结果的正确性. 3.4.1 主从核异步并行 上述优化都是基于主从核加速并行的模式,即主核将计算迁移到从核之后进入等待状态,直到从核计算执行完毕后醒来继续执行.而这种模式未能发挥主核计算能力,所以我们采取主从核异步并行的模式充分利用主核.为充分利用DMA的传输带宽,我们将连续块数据访问模式的计算放置到从核,同时主核负责独立片段式数据访问模式的计算,从而实现主从核异步并行模式,例如从核在计算网格插值力过程的同时,主核计算非相关的能量规约. 3.4.2 数据复用 在最初移植的从核版本中,FFT网格参数及逆FFT网格参数需要被频繁地计算并传输到从核进行使用.而在单步计算过程中,这些参数并不会改变.所以我们在单步起始处计算这些参数值,合并数据并打包,通过DMA通信直接传输到从核局存进行缓存,从而减少对参数数据的访存开销. 3.4.3 优化从核的空间开辟 由于PME算法涉及很多数据结构(包括原子序列、B样条、三维网格等),所以在从核计算前需要大量地使用malloc函数进行空间开辟.而每次进行空间开辟与释放都需要大量的时间,所以我们在从核局存直接开辟56KB的空类型空间,并使用指针外加强类型转换为每个数据结构指定一块内存空间,那么每次调用从核函数时只需要一次空间开辟及释放即可. 本文实验平台为SW26010众核处理器和Intel(R)Xeon(R)CPU E5-2660处理器,具体的软硬件环境配置如表1所示. 表1 软、硬件环境配置Table 1 Software/Hardware environment configuration 实验主要对比申威主核、从核版本及CPU的串行执行版本的性能并进行分析.其中GROMACS的测试版本为5.1.5,测试算例4Q21是经典的生物实验蛋白模拟,因其结构变化容易观察,现已在实际生物实验中获取它的主要构象,适合用来验证计算模拟效果的优劣.并且该蛋白为著名的抗肿瘤药物靶标蛋白,对它的研究具有重要的生理学意义.其中算例总原子数为28161,采用显溶剂模型,系综为NVT. 4.2.1 不同模块间优化分析 第1组对比实验设置在申威平台对比分析优化前后不同模块的性能提升.本文使用O3、内联等编译选项调优后的GROMACS代码作为初始版本,各模块性能对比测试如图7所示.其中spread、solve、gather分别对应PME算法中电荷扩散、静电势能计算和网格插值力的模块,total代表整个PME过程. 从图7可以看到,主核向量化对比初始化版本提升并不大,其中性能提升最大的是solve模块,加速了1.5倍.我们在主核向量化版本的工作主要是针对模块内的核心计算部分进行循环展开和SIMD并行.而spread模块的计算部分集中在样条值的求解及网格点累加电荷贡献值部分,但是由于沿原电荷序访问的不连续网格点存在空间离散性,导致主核cache利用率极低,向量寄存器加载时间长,从而提升效果不佳.gather模块的计算部分集中于根据网格点插值求粒子受力的过程,与spread模块有一样的问题.而由于solve模块是计算密集型的且访存效率高,所以较其他两个模块提升效果好,但是由于超越函数耗时高导致优化效果不明显,也只有1.5倍的性能提升. 图7 模块优化前后对比图Fig.7 Module optimization comparison 从核对比初始化版本在各模块提升明显,平均性能提升了8.85倍.其中spread模块在原程序中存在写写冲突等问题而导致不易并行,我们通过引入局部网格序的从核分块策略,维持数据空间局部性的同时消除了写写冲突,但是由于额外引入了排列开销,所以提升并不显著.solve模块的主要开销在于计算,在用多项式近似方法优化了从核超越函数之后,相比主核有40.13倍的提升.在对从核数据进行重组之后,gather模块内的访存变得连续,性能提升了9.6倍. 4.2.2 不同平台间优化分析 第2组对比实验建立在SW26010与Intel(R)Xeon(R)CPU E5-2660两个不同平台的结果对比上,如图8所示. 图8 不同平台性能对比图Fig.8 Performance comparison between platforms 其中cpu-none和cpu-sse4.1分别代表CPU的非向量化版本和使用SSE4.1指令集优化的向量化版本.从图8可以看出,Intel CPU的向量化优化提升了1.24倍,与申威主核向量化优化的性能提升相近,这是由于算法本身的访存特性决定的.并且最终从核版本的PME算法性能相较于CPU向量化版本提升了1.2倍. 尽管从核的性能高于CPU向量化版本,但PME算法在从核上的运行效率低于Intel CPU.经测试发现,算法的性能有以下3方面的限制: 1)PME算法内有大量的访存操作,而主从核DMA传输的带宽低于CPU访存的带宽,导致访存受限. 2)引入局部网格序提高数据局部性和解决写冲突的同时,也引进了排序开销和冗余计算,需要进一步优化算法最小化性能损失. 3)在网格插值求受力的过程,从核将计算完的局部网格序的力数组传回主核,由主核将受力映射到原电荷序的力数组.由于写回的数据量较大,由主核处理会带来一定的性能损失,但目前还没有更好的解决方案. 本论文首次尝试将GROMACS的PME算法移植到SW26010众核处理器上,并根据芯片体系结构及算法特点提出基于局部网格序的分块策略等方法进行移植优化.通过实验证明优化后的从核版本相较于主核有8.85倍的性能提升,相较于CPU有1.2倍的性能提升.PME算法广泛应用于分子动力学模拟程序,本工作可以为相关应用的优化提供参考.此外,局部网格序的设计方法也可以为神威太湖之光上涉及散乱数据插值的应用优化提供借鉴.未来,我们将进一步使用更底层的编程方法来深度优化PME算法的性能,并在神威太湖之光上对PME算法进行强扩展性的优化与测试.3.4 其他优化
4 实验结果及分析
4.1 测试环境及算例

4.2 测试结果及分析


5 总 结

