微学习单元因果关联发现的点互信息判据研究

刘 腾，陈 健，张月琴，王 莉

1(太原理工大学 大数据学院，山西 晋中 030600) 2(太原理工大学 信息与计算机学院，山西 晋中 030600)

1 引 言

关联规则发现的研究在电子商务领域得到了广泛的应用，电商通过关联规则来发现商品间的关联关系，并根据用户已购的商品，把关联关系密切的其他商品推荐给用户.这种关联关系不仅存在于电子商务的商品之间，同样也存在于在线教育领域的学习内容之间.

众所周知，当前知识更新周期正逐步缩短.移动技术的发展，促使内容短小、形式多样的学习信息可被轻松发布到互联网.这促生了微学习这一新颖的学习方式[1].微学习以其微内容、微时间、微过程、微媒介、微资源等特点[2]，使学习者可以更便捷、合理地利用碎片化时间学习，为解决学习时间碎片化、学习场所自主化等问题提供了很好的方案.但是，微学习单元的分散化，海量和多源异构等特性也导致了学习内容筛选的困难.关联规则发现的研究成果，则为发现微学习单元间的关联关系提供了有效的手段.

然而，关联规则发现中使用的核心指标支持度，该指标虽然能反映出两者间的关联紧密程度，却不能发现购买商品的先后顺序.与商品购入存在顺序相似，学习是一个由易到难的循序渐进的过程，对学习资源的学习也需从易到难进行学习.根据学习者的能力来组织学习资源的顺序，可以帮助学习者提高学习效率.多项研究表明建立在学习单元之上的不同学习路径会导致不同的学习结果[3]，如果以合适的方法对学习资源进行难易筛选和先后排序，并为学习者提供导航，可以有效提高学习者的效率.

学习路径是指学习活动的路线与序列[4]，是学习者在一定的学习策略指导下，根据学习目标和学习内容对所需完成的学习单元的排序.学习路径规划是帮助学习者提高学习效率的重要手段.其中通过序列模式发现算法进行学习路径推荐是重要的分支之一[5].序列模式发现是基于关联规则核心思想实现的，通过关注学习序列的频率进行学习路径推荐，该方法没有考虑学习单元间的相互作用，也不能针对指定目标进行路径规划.而微学习单元有多源分散等特性，如何深入关注学习单元间的相互作用，以目标为驱动进行学习路径规划成为一个新的问题.

两个先后发生的事务之间通常有着某种关联关系，多数情况下这种关系被称为前因后果关系，或简称因果关系.尽管目前还不能确保是否所有前后发生的事务都存在因果关系，但也无法证明两者之间不存在相互作用.因果关联关系在相关性方面可以说明关联关系前件和后件的因果关系，在时序方面可以说明关联关系的前件先于后件的发生，正因如此，因果关联关系机制可以发现变量之间隐含的更深层次的递进关系，即可以反映出微学习单元之间内容上的因果关系和学习时序的先后关系.因此，本研究将因果关系引入关联规则的发现中，深入研究微学习单元间内在关系，并以此进行学习路径规划，以支持个性化学习.

2 相关研究

2.1 关联规则

关联规则是变量之间相关性发现重要方法，它已被广泛应用于物理、医学、教育等各个领域.自Agrawal等人提出基于频繁项集的经典关联规则Apriori算法后[6]，国内外研究人员都对关联规则挖掘问题进行了深入研究.不过目前关联规则主要是通过支持度-置信度框架来计算事务间的集中频度从而得出相应的规则，但是研究者在实践应用中发现，传统的支持度-置信度框架会产生多冗余、低精度的规则[7]，进而影响决策.所以诸多学者希望通过改进支持度-置信度框架来解决这一问题.如Wang等人为更好的筛选有效规则，通过比较支持度与置信度间大小的方法提出了置信因子，从而达到去除不相关事务和负相关事务的目的，改进了传统的支持度-置信度框架[8]；Malarvizhi等人将关联规则与网络日志挖掘的应用场景结合，根据用户在不同Web页面停留的时间为其分配权重，提出T+树的加权方法对支持度和置信度进行加权，可以更好的发现频繁项集、筛选规则，降低了计算时间，改进了支持度-置信度框架[9]；Tahyudin等人介绍了采用粒子群算法优化关联规则的方法，并引入柯西分布与粒子群算法相结合来解决数字关联分析中的局部最优问题[10]；韩楠等人为解决关联规则过频繁的问题引入了最大支持度，并通过改进FP-Growth算法挖掘负关联规则[11].上述方法仍只关注于事务间的集中频度，没有对事务间的内在作用和先后顺序进行研究.

2.2 点互信息与因果关系判据

因果关系相对于相关关系是对问题更深层次的认识，是事务之间相互作用的描述[12].传统的因果关系发现方法是以时序和统计为基础，成本较高，且受实验技术和社会道德等因素干扰，所以基于观测数据的因果关系发现更加客观和易于实现[13].在微学习领域，Reich曾预测因果关系的发现将是在线教育研究的重要方向[14]，而微学习单元间的因果关系，体现在内容上的依赖关系与学习时序的先后关系.

然而先后关系不等于因果关系，为准确描述因果关系，Silverstein等人提出了一组因果规则的定义：CCU(CCU Causality)因果规则和CCC(CCC Causality)因果规则，根据变量之间的关系进行因果关系判断[15].

1)CCU因果规则判据

给定3个变量A、B和C，如果变量A、B和B、C分别相关，且A、C不相关，同时A、C在B成立时存在相关性，可得因果规则为：A→B←C;即，有因果关系A→B和C→B.

2)CCC因果规则判据

CCC因果规则判据与CCU因果规则判据相似，但变量A、B和C之间两两互为相关，如果给定变量B后，A、C独立.则其因果规则为：

A→B→CA←B←CA←B→C

同理，A、B和C之间的因果关系为上述3种情况之一.

CCC和CCU因果规则自发表后受到广泛关注，但在实际应用中则遇到因果关系判据的适用性问题.传统的关联规则算法虽然能够发现事务间的关联关系，但不能发现诸如因果关联这样的关系.

点互信息是信息理论和统计学中使用的一种关联度量.通过量化离散随机变量A、B间联合分布概率和其各自独立分布概率的差异来衡量变量之间的关联性.公式(1)为变量A、B间点互信息计算公式.

(1)

为了使点互信息有固定的上限并降低其低频偏置，对点互信息进行归一化，将其取值范围限定在[-1,1]之间.公式(2)为归一化点互信息计算公式.

(2)

通过点互信息可以表达变量之间关联程度的特性，可以描述因果关联规则CCU和CCC的结构特征，使传统关联规则可以采用因果关系判据进行规则发现和筛选.

而微学习单元间存在相互影响、知识的承前继后等关系，为此，本研究在关联规则和因果关系的基础上，提出基于点互信息的因果关联关系判据算法.该算法可去除冗余规则，并从中发现微学习单元间的因果关联关系，进而完成有效的学习路径规划和管理.

3 提案相关定义及因果关联规则

微学习提出至今，国内外学者对微学习进行了大量的研究.早期微学习的研究侧重于概念和其支持技术[16]；近年来，微学习的研究分别扩展到两个领域，即应用技术和微学习相关教育理论.在应用技术方面，推荐系统的研究是重要的组成部分；但是，目前关于微学习推荐系统的研究仍处于起始阶段.

一些研究者通过改进经典推荐算法将其应用在微学习领域，如Chen等人提出一种混合推荐算法来反映学习过程中的时效性[17]，而Shu等人采用卷积神经网络来训练推荐子模型[18].另一些研究者通过结合微学习理论体系来设计推荐算法，如建构主义学习观(Constructivism Learning Theory)认为微学习单元间是有关联的，可以根据领域知识和学习过程的顺序来描述这种关系[19].如Hassani等人将关联规则的方法应用到学习过程中数据的相关性发现[20].Shen等人使用基于贝叶斯网络的方法来发现学习单元之间的相关性，并实现学习路径的动态规划[21].

基于上述分析，本研究提出一种建立在CCC和CCU因果关联规则上，通过点互信息为判据的方法，以发现学习单元间的因果关系.以下是与提案相关的两个定义.

3.1 学习周期与微学习路径

为了更好的发现学习单元间的因果关联关系，本研究根据学习者的学习目标定义了学习周期和路径.

定义1.学习周期是指学习者为了达成一个学习目标而进行的一个从开始学习到完成学习的期间.该期间由开始学习第一个微学习单元开始，到通过完成相应测验，达成学习目标结束.

定义2.微学习路径是指在一个学习周期内学习者所学习的微学习单元会组成一个微学习单元的序列，这一序列被称为达成该学习目标的微学习单元路径.该路径中包括为达成学习目标的标准学习路径中的学习单元，也可能含为达成目标而学习的前置知识单元或标准学习路径的学习单元以外的多源异构单元.

由于在学习过程中对同一个学习单元进行重复学习时，关注的重点是不一样的.因此，本研究把对同一微学习单元的重复学习视为各自独立的事务.

3.2 微学习单元因果关联规则

微学习单元是达成一个教育目的的最小学习内容的集合，通过基础数据描述集合本身及教育用途[22].这些微学习内容之间存在承前继后的关系；高级知识依赖基础知识，导致学习时序上的先后关系；先学基础知识再学进阶知识.

微学习内容存在不同的发布者，使微学习内容存在多源性，从而增加学习者选择学习资源的负担.

在对微学习单元进行学习的过程中，每个学习者在完成一个微学习单元后将选择下一个微学习单元.选择过程通常是依据学习者的前置知识、学习目标、学习习惯等个性来进行的.一部分学习者，具备良好的前置知识，仅需依据发布者提供的标准路径进行学习即可.而缺乏前置知识的学习者，则需学习含有前置知识的微学习单元，或在出现知识遗忘的情况下重复学习以前学过的学习单元，并在此基础上，继续完成后续学习，进而完成学习目标.这意味着微学习单元的因果关联规则不仅取决于学习内容本身的关联性，而且与学习者的个性相关.所以，本研究认为微学习单元之间存在的因果关联关系是基于学习者个性化学习来表现的.

4 以点互信息为判据的因果关联关系发现

在对相关研究的分析基础之上，本研究提出一种基于点互信息的因果关联关系发现判据.

4.1 以点互信息为判据的微学习路径规划框架

本文通过对学习者的学习历史数据进行关联规则发现和因果关系分析，得到因果关联关系约束网络.其步骤为，对学习者的历史数据进行预处理后，使用经典关联规则的方法获得频繁项集，以此建立相关性约束形成约束网络图解模型，进而在CCU和CCC因果关系规则的基础上，提出一种新的基于点互信息的因果关系判据，对图解模型进行因果关系发现和剪枝，最终得到了因果关联关系约束网络.

图1 以约束网络因果关联关系算法为基础的路径规划框架Fig.1 Path planning framework based on constrained network causal association algorithm

图1为利用因果判据的路径规划框架图，基于点互信息的约束网络因果关联关系发现框架包括4个模块：数据预处理模块，相关性发现模块、构建因果关联关系约束网络模块和路径规划模块.

4.1.1 数据预处理模块

学习者的历史数据通常记录了学习者的操作内容与时间等信息，为了保证学习者的隐私和便于算法的实施.本研究对不同的学习者和学习单元采用不同的编号来表示.表1是微课程1的微学习单元序号，其含意为微课程1由8个微学习单元组成.

表1 微学习单元示例Table 1 Examples of micro-learning units

根据学习周期的定义，从微课程1中最少可有8个学习周期.同时，根据学习成绩对学习者进行分组，认为具有相似成绩的学习者具备相似的前置知识和学习方法.是相似学习者.不同成绩水平的学习者具有不同的个性化表现，体现在学习单元的关联上即有不同的因果关联关系.表2为成绩分组方案.参照高校的评价标准，本研究将成绩水平分为表2所示的4个等级.

表2 得分水平分组表Table 2 Grouping of scores

4.1.2 相关性发现模块

频繁模式是满足最小支持度阈值的事务集合，是发现事务相关性的主要环节；同时，频繁特征作为判断因果候选集的一个标准，可以在发现频繁项集的基础上进行因果规则的发现.相关学者已经提出频繁项集发现的多种可行方案，本研究采用经典的Apriori频繁模式发现算法，获取微学习单元之间的频繁项集，发现微学习单元间的相关性.

4.1.3 构建因果关联关系约束网络模块

通过以微学习单元间相关性为约束构成相关性图解模型，并对其进行条件独立性判断，剪去在已知第3个节点情况下另两节点独立的边，为后续因果判断奠定基础.基于点互信息的CCU和CCC因果关系判据是基于约束的观察数据局部因果发现算法，相较于其他因果算法更能反映数据之间的约束和联系，且其是基于统计方法的，有更好的鲁棒性.

依据因果关系判据结果对相关性图解模型进行剪枝，保留具有因果关系的节点间的边.然后，依据学习目标和因果关系确定节点间边的方向，形成节点间具有因果关联性的因果关联关系约束网络.

4.1.4 路径发现模块

根据因果关联关系约束网络进行微学习路径规划.为了在因果关联关系约束网络中规划较优的微学习路径，本文定义了因果关联关系依存度和微学习路径强度.

定义3.因果关联关系依存度(Causality Degree of Dependence,CDD)是指因果关联关系中前件和后件的依存程度，用其后验概率表示.如存在因果关联关系A→B，A为前件，B为后件；其依存度表示为发现该关系数据集中的后验概率P(B|A),见公式(8).

定义 4.微学习路径强度是指组成该路径的所有因果关联关系依存度的均值.如存在路径A→B→C，组成该路径的因果关联关系有：A→B和B→C；则其路径强度如公式(3)所示.

(3)

其中，P(B|A)为A→B的因果关系依存度，P(C|B)为B→C的因果关系依存度.因果关联关系约束网络中所有可以实现学习目标的微学习路径，路径强度较大的优先推荐.

4.2 算法设计

本文基于图1约束网络因果关联关系发现框架，提出了一种基于点互信息判据发现微学习单元间因果关联关系的算法.该算法是通过将关联规则和因果关系引入到约束网络中，以点互信息作为发现因果关联关系的判据，并依据此进行微学习路径规划.具体实现伪代码如算法1所示.

算法1.约束网络因果关联关系发现算法

输入：不同个性学习者的学习记录和学习单元基本信息数据集Dd={item1,item2,…,itemn}(d={A,B,C,D})，最小支持度阈值s，CCU和CCC因果度阈值Cs={ccu,ccc}，学习目标Y=[y1].

输出：学习单元间因果关联关系集合R={}和最优学习路径序列P=[n].

1.初始化R，P

InitialR,Pas an empty set;

//遍历不同个性学习者的学习历史数据集

Fordin {A,B,C,D}

2.调用算法2相关性发现算法，获得相关性学习单元集合

//获取具有相关性的微学习单元的集合

F=CD_Algorithm(Dd,s);

3.调用算法3基于点互信息判据的因果关联关系约束网络生成算法，生成因果关联关系约束网络

//获取因果关联关系约束网络邻接矩阵

MGraph=GCACN_Algorithm(F,Cs,Y);

//获取因果关联关系集合

R=GCACN_Algorithm(F,Cs,Y);

4.调用算法4路径规划算法，生成优化学习路径序列

P=MLPP_Algorithm(MGraph);

End

算法1为约束网络因果关联关系发现算法，其功能由3个主要子算法实现，即调用相关性发现算法、因果关联关系约束网络生成算法和路径规划算法.

4.2.1 相关性发现算法

相关性发现算法主要是发现微学习单元间的相关性，本文采用经典的Apriori频繁模式发现算法进行相关性的发现.具体伪代码如算法2所示.

算法2.相关性发现算法(CD_Algorithm)

输入：学习者的学习记录和学习单元基本信息数据集Dd={item1,item2,…,itemn}(d={A,B,C,D})，最小支持度阈值s.

输出：具有相关性的微学习单元的集合F.

1.初始化相关性的微学习单元的集合F

InitialFas an empty set;

2.发现频繁1项集

ForitemiinDd:

//保留满足支持度阈值的频繁1项集

L1=L1∪{itemi,P1i};

3.连接生成候选2项集

ForiinL1

ForjinL1

i≠j:C2=C2∪{i,j};

4.生成具有相关性的微学习单元的集合F

//发现满足支持度阈值的相关单元

Fori,jinC2

If support(i→j)>s

SetF=F∪[i,j];

End

4.2.2 基于点互信息判据的因果关联关系约束网络

根据微学习单元的相关性构建相关性图解模型，并对其进行条件独立性判断，对图解网络进行剪枝.公式(4)为条件独立性检验公式.

P(A,C|B)=P(A|B)P(C|B)

(4)

如公式(4)所示，当微学习单元A、C在单元B发生的条件下同时发生的概率与其在单元B条件下分别发生的概率积相等，则认为学习单元A、C条件独立，其间不具备相关关系.完成独立性检验后，因果关系的发现是重要的一环，为了使因果关系的判定更好的改进传统的关联规则的发现，本文基于点互信息和CCU算法、CCC算法的结构特征提出因果关系度量：CCU因果度和CCC因果度.公式(5)为CCU因果度计算方法.

CCU(A,C|B)=min(NPMI(A,B),NPMI(B,C),NPMI(A,C|B))-NPMI(A,C)

(5)

其中NPMI(A，B)表示变量A、B的归一化点互信息，用来说明A、B之间的相关性；NPMI(A，C|B)表示在给定变量B后A、C变量的相关性.根据CCU算法的结构特征，因为变量A、C之间相互独立，所以NPMI(A，C)值应较小，而变量A、B间关系，B、C间关系和在B条件下A、C间关系均为相关，所以NPMI(A，B)，NPMI(B，C)，NPMI(A，C|B)值应较大，且均大于NPMI(A，C)值，即CCU(A，C|B)>0.如此，便通过点互信息表达出CCU结构，在CCU(A，C|B)因果度满足阈值时可以得到因果关系：A→B和C→B.

公式(6)表示B存在后A、C的归一化点互信息计算公式，其中P(A，C|B)表示在B条件下A，C的条件概率.

(6)

同理，根据CCC算法的结构特征，提出CCC因果度.

CCC(A,C|B)=min(NPMI(A,B),NPMI(A,C),NPMI(B,C))-NPMI(A,C|B)

(7)

通过CCU因果度和CCC因果度即可对相关性图解模型进行因果判断.具体伪代码如算法3所示.

唯一不同的是，满足CCC因果度仍不能确定变量之间的唯一因果关系.只能说明，存在的因果关系仅为以下情况的一种：

A→B→C或C→B→A或A←B→C

根据以目标为驱动的学习周期特性，为达到学习目标对其前置知识等多源异构学习单元进行学习，本文将学习目标作为因果规则的后件.同时，本文提出根据观测数据来确定因果关系的方向，用最大后验概率判断因果方向.后验概率计算方法为公式(8).其中A表示因果关联关系前件，Bi表示后件，则当P(Bi|A)最大时Bi的取值方向即为因果方向.

(8)

上述3种情况中如果学习目标为C且后验概率P(B|A)值最大，则因果关系为：A→B→C.

根据微学习单元间因果关系判断结果，对微学习单元相关性图解模型进行剪枝，并结合学习目标对因果关联关系方向确定；构建因果关联关系约束网络.具体伪代码如算法3所示.

算法3.因果关联关系约束网络生成算法(GCACN_Algorithm)

输入：具有相关性微学习单元的集合F=[[item1,item2],[item3,item4],…]，学习目标Y=[y1]，CCU和CCC因果度阈值Cs={ccu,ccc}.

输出：学习单元间因果关联关系集合R={},因果关联关系约束网络邻接矩阵MGraph[].

1.初始化因果关联关系约束网络邻接矩阵

InitialMGraph[];

2.设置图节点集合

Nodes=set(Nodes.apped(fornodeinF));

3.建立相关性邻接矩阵

UGraph：Generate djacency matrix based onF；

4.进行独立性检验

ForA,B,Cin Nodes

ForA,B,CinUGraph

//根据公式(4)去除条件独立节点间的相关性

If nodeA,B,CSatisfy Formula(4)

UGraph[A][C]==0;

5.因果关系判断

MGraph=UGraph;

Fornodein Nodes

FornodeinMGraph

//设置学习目标单元

B=Y;

IfMGraph[A][B]>0 andMGraph[C][B]>0

//变量间满足CCU因果结构

IfMGraph[A][C]=0

//通过公式(5)计算CCU因果度

Set CCU(A,B,C)based on formula(5);

//CCU因果度不满足阈值，不存在因果关联

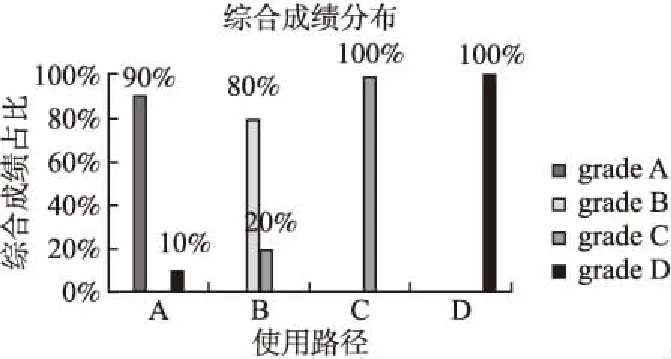
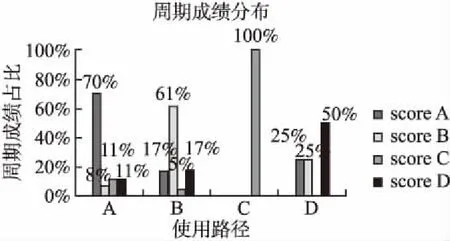
If CCU(A,B,C)

MGraph[A][B]=0;

MGraph[C][B]=0;

Else

//CCU因果度满足阈值，根据公式(8)计算因果关联依存度(CDD)

Determine the strength of rule(R.CCD)

based on Definition 3 and Formula(8)

//因果关联关系R的依存度R.CDD设为矩阵中对应关系的值

MGraph[A][B]=R.CDD;

MGraph[C][B]=R.CDD;

//根据新的因果关联设定学习目标单元

Y=[A,C];

//变量间满足CCC因果结构

Else

//设定目标学习单元，计算CCC因果度

C=Y;

Set CCC(A,B,C)based on Formula(7);

MGraph[A][C]=0;

//CCC因果度不满足阈值，不存在因果关联

If CCC(A,B,C)

MGraph[A][B]=0;

MGraph[C][B]=0;

//CCC因果度满足阈值，根据学习目标和后验概率确定因果关联

Elif P(B|A)>P(A|B)based on Formula(8)

MGraph[A][B]=R.CDD;

MGraph[B][C]=R.CDD;

Y=[A];

Else

MGraph[B][A]=R.CDD；

MGraph[B][C]=R.CDD；

Y=[B];

6.从有向图中生成因果关联关系

Fori,jinMGraph

IfMGraph[i][J]>0

R=R∪(i→j);

End

4.2.3 路径规划算法

根据因果关联规则约束网络和定义4进行微学习路径规划.具体伪代码为算法4.

算法 4.路径规划算法(MLPP_Algorithm)

输入：因果关联关系约束网络邻接矩阵MGraph.

输出：微学习单元最优学习路径序列P=[n].

1.生成学习路径

P′:Generate pathP′ based onMGraph

2.计算路径强度

//从矩阵中获得路径中各关系的依存度，并求和

ForR.CDDinMGraph

R.CDDsum=R.CDDsum+R.CDD;

//计算路径中各关系依存度平均值，即路径强度

P′.strength=avg(R.CDDsum);

3.推荐学习路径

//获得路径强度最大的路径

IfP.strength==max(P′.strength)

Output recommended pathP;

End

5 实验设计和结果分析

为了验证本文提出的算法在微学习领域的应用，发现微学习单元之间的因果关联关系，为学习者提供个性化学习路径，本研究使用学习管理系统(Learning Management System，LMS)Moodle(Modular Object-Oriented Dynamic Learning Environment)平台为学习者提供服务，并收集学习者的学习历史记录进行实验和评估.Moodle是著名的模块化的面向对象的动态学习环境平台；不仅可以为学习者提供线上学习环境，具有在线学习、论坛讨论、在线测验、自我反馈等交互学习功能；而且还可以为课程管理者提供课程管理、日程管理、学习日志记录和简单数据可视化等功能.Moodle平台很好的模拟了微学习环境，可以为学习者提供良好学习服务的同时进行数据收集和学习记录追踪.因此，本文选用Moodle作为实验平台.

5.1 实验设计

本文从两方面对提案算法在微学习领域的应用进行了验证.

1)验证提案算法发现微学习单元间的因果关联关系的准确性.

2)验证通过微学习单元间的因果关联关系为学习者规划学习路径的有效性.

为了验证达成学习目标的过程中，学习单元间的因果关联关系；本文采用学习目标的前置知识单元和学习目标单元作为学习资料供近150名学习者进行学习.得到40000余条学习记录和每个学习者的学习周期测验成绩、最终测试分数.根据表2中所示的成绩水平将用户分成4组，并且每组数据被细分为两个数据集：参考组学习记录数据集和验证组学习记录数据集.其中有60名学习者的数据集构成验证组学习记录数据集，以对本提案算法进行验证.

根据学习周期的定义，微课程1中获得8个学习周期，每个周期均进行测验，检验其对目标知识掌握程度，并对掌握水平进行分组.表3中是微课程数据集中单个学习者的学习记录和学习成绩的示例.User表示用户序号，Course为课程序号，Period表示学习周期，而Unit表示微学习单元序号，单元序号的下标表示访问顺序.Test score为学习周期测验成绩，Test Group是根据表2划分周期测验成绩的水平；Grade是学习者学习微课程的总成绩，同理，Group是反映了总成绩的水平等级.

5.2 实验结果和分析

在微课程中，根据专家对微学习单元之间的关系进行认证，已知微学习单元间有19组因果关系.通过应用提案算法对实验数据进行分析，使用正确率、召回率和F1值作为评价指标[23]，评价得分在0-1之间，越趋近于1说明与专家标记的因果规则误差越小.结果发现，该算法发现的微学习单元间的因果关联关系有73.7%与专家标记一致.表4为基于观测数据发现微学习单元间的因果关联关系情况.

表3 实验数据部分示例Table 3 Examples of experimental data

表4 基于观测数据发现微学习单元间的因果关联关系情况Table 4 Finding causal associationamong micro-learning units based on observed data

经典算法Fast-DTW适用于两条不同长度和不同频率的时间序列的相似度计算[24]，本文采用该方法计算学习路径之间的相似性.通过计算不同的微学习路径之间的Fast-DTW距离，进行路径相似度判断.如果该值较小，则意味着两条路径的相似度较高；相反则其相似度较低.本研究通过提案算法对参考组中各组数据进行分析，得出相应A、B、C、D 4类推荐学习路径.计算验证组中实际路径与参考组4条推荐路径的Fast-DTW距离，并认为其与Fast-DTW距离最小的推荐组路径最相似，为同一类学习路径.由此，实验发现在验证组中采用与推荐学习路径同一类型的学习路径学习，其成绩与参考组中推荐路径所对应的学习成绩处于同一水平.验证组中所有学习者使用学习路径与成绩分布的对应情况表示见图2.

图2 验证组学习者采用推荐路径类型与成绩水平对应关系Fig.2 Relationship between the type of learningpath and learningachievement level adopted by learners

图2中，横轴表示验证组学习者采用学习路径的类型，纵坐标表示验证组学习者采用不同类型路径学习后，成绩的占比情况.根据其学习路径的不同分析其成绩分布，由图2所示，验证组中使用路径类型A的学习者有90%取得了等级为A的成绩，使用路径类型B的学习者有80%取得了对应成绩，验证组中使用路径类型为C或D进行学习所取得成绩完全与其路径类型相对应.由此说明采用适合的学习路径有助于取得相应的成绩.本文对学习者采用学习路径的类型与取得成绩水平的匹配程度进行了分析，实验发现84%的学习者取得与推荐学习路径相符的学习成绩.

同理，通过提案算法对参考组中不同周期及按其成绩水平分组的数据进行分析，发现多数学习者的周期测验成绩水平与周期推荐路径相符，周期推荐学习路径与该周期的测试成绩对应情况为图3所示.其中70%使用路径A的学习者路径类型与周期成绩等级相符，61%使用路径B的学习者成绩与路径类型相符，而使用路径C的学习者路径与周期成绩完全相符，一半使用D路径的学习者路径类型与周期成绩相符.同样，本文对学习者采用学习路径的类型与取得周期测验成绩水平的匹配程度进行分析，实验发现有68%学习者取得与推荐学习路径相符的学习成绩.

图3 学习者采用推荐周期路径类型与周期成绩水平间关系Fig.3 Relationship between the type of learningcycle path and learningcycle achievement level adopted by learners

由实验结果可知，提案算法所得学习路径在验证组中同样有效，大部分学习者的学习成绩受学习路径影响，采用适合的学习路径学习会取得相应的成绩.上述实验证明本提案算法可以发现大部分微学习单元间的因果关联关系，该算法发现的学习路径规划对多数学习者是有效的，可以针对不同的学习者进行路径规划和推荐，以更加符合其学习个性，提高学习效率.

6 结束语

本研究在约束网络、关联规则发现和因果关联规则的基础上，提出了一种基于点互信息的因果关联关系判据，用于发现微学习单元间的因果关联关系，并以此规划个性化微学习路径.实验结果表明，该算法可以有效的发现微学习单元间的因果关联关系，并且基于此进行规划的微学习路径在参考组和验证组中有较高的相似性，可以通过该方法进行个性化微学习路径推荐.在今后的工作，拟通过实时学习环境，来验证本提案的学习优化方法，并更加具体的研究学习者与优化学习路径的关系，以达到更高效的个性化学习路径推荐.