实时操作系统中有限优先级反转的验证

张 啸 然

1(中国科学技术大学 计算机科学与技术学院，合肥 230027) 2(中国科学技术大学 苏州研究院软件安全实验室，江苏 苏州 215123)

1 引 言

优先级调度算法是实时操作系统中常用的一种调度算法.这种调度算法始终选择最高优先级的就绪态中优先级最高的任务执行，基于这种性质，用户可以分配给不同任务不同的优先级来确保任务的实时性得以满足.然而，当系统中同时使用了优先级调度与信号量同步机制时，由于阻塞的产生，会导致优先级反转问题：拥有高优先级的任务会被低优先级的任务无限制的阻塞.图1给出了一个简单的优先级反转问题的例子.

假设t1,t2,t3是3个按优先级从低到高排列的任务.在开始阶段，只有任务t1执行，在其执行的过程中，他获取了信号量s.之后任务t3被创建，由于t3的优先级大于t1，调度器会让t3优先执行.在t3运行一段时间后，他也需要获取信号量s，但由于此时任务t1已经得到了信号量s，所以他只能等待t1释放信号量s.由于此时t3进入了等待状态，系统会切换到t1执行.在t1执行一段时间后，任务t2被创建，由于t2的优先级大于t1，t2会被优先执行.如果此时t2是一个永续的任务，那么此时t3会被永远的阻塞.这时，一个典型的优先级反转问题发生了：t2的优先级低于t3，但其却永远的阻塞了t3的执行.

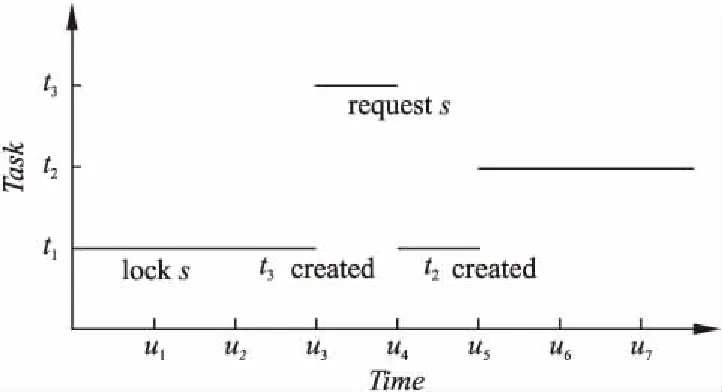
图1 无限优先级反转Fig.1 Unbounded priority inversion

为了解决这个问题，Sha等人[1]中提出了优先级继承协议与优先级天花板协议.并分别给出了这两种协议中高优先级任务会被低优先级任务所阻塞的最长时间.在这之后，也有各种各样的用于避免产生无限优先级反转问题的协议被提出.如Baker[2]就提出了栈资源协议，用于只在栈上分配资源的同时避免此问题.Chen等人[3]也提出运用动态优先级天花板的新思路.而常被参考的IEEE的POSIX操作系统标准中也给出了两套建议的协议规范(优先级继承协议与优先级保护协议)来解决这个问题.

然而由于这些协议设计的较为精妙，在实现的过程中一些细节常常被忽略而导致错误的产生.Yodaiken[4]中就指出，在Sha等人[1]给出的最早版本的优先级继承协议代码实现中实际上在一些情况下是错误的.Xu等人[5]中也指出只有当信号量同步机制不被嵌套使用时，操作系统μC/OS-Ⅱ中所实现的防止优先级反转协议才有作用.虽然目前已经有了关于避免优先级反转问题的一些验证工作[7-10]，但该工作依然未能做到验证底层真实的代码.

本文将给出一套保证有限优先级反转性质的验证框架.该系统的整体性概览可参见图2.一套防止无限优先级反转问题的协议，可以看作图中高层代码抽象部分.其是否能够保证有限优先级反转性质可以看作为使用该规范的系统在执行时是否所有的执行迹都满足有限优先级反转的定义(图中①和②).但由于这样的证明过程往往过于复杂，本文提出了合理OS实现的定义，并证明了如果静态协议抽象可以满足该定义，那么使用该套协议所可能产生的所有迹均可满足有限优先级反转(图中③和④).图中的下半部分给出了本文对于具体底层代码层面验证的思路.本文在第六章中提供了一套验证逻辑，该套逻辑能够用于证明底层代码生成的迹与对应的高层代码间具有子集关系.这样，自然的也就得到了底层代码具有有限优先级反转性质.最后，作为实例，本文验证了POSIX标准中提供的两个用于保证有限优先级反转的协议——优先级保护协议和优先级继承协议.此外，由于本文中所提到的所有工作均通过了验证辅助工具Coq的检验，因此文中省略了具体的定理证明部分.

相比之前的工作，本文的工作具有以下几点贡献：

1)本文基于代码执行过程中产生的迹给出了一个协议无关的有限优先级反转的形式化定义，此定义可以被同时运用在抽象机器层面与实际机器层面.

图2 概览Fig.2 Overview

2)本文建立的框架提供了一套抽象语言.用户可以用此语言简单的描述出算法协议.此外，本文给出了一套基于该语言的辅助定义“合理OS实现”并证明了该定义蕴含有限优先级反转.对于一个协议，用户可以通过证明协议满足该定义来就简单的得到协议可以保证有限优先级反转性质.该证明方案大大降低了证明有限优先级反转问题的难度.

3)本文给出了一套程序逻辑用于证明底层C代码实现与高层抽象语言之间的精化关系.此精化关系可以传递有限优先级反转性质，从而使得对于此问题的验证可以被用于底层.这也是第一次能够做到在实际机器层面保证该性质.

4)通过应用该验证框架，作为实例，本文在最后证明了POSIX标准中的两套协议确实能够防止无限优先级反转的问题.并且对于这两套协议分别给出了对应的底层C代码实现，并证明了它们间的精化关系.

2 相关工作

目前已经有了数个工作与本文的工作相关.但这些工作都没有在实际的代码层面对该问题进行验证.此外，以已有的工作都是面向特定的协议进行验证的，而本文的工作则更为宏观的提出了一套可用于验证多种防止无限优先级反转协议的方案.

Zhang等人基于Isabelle/HOL的项目[6]是最接近本文的.该项目引入了一个记录每个操作的迹(包括了获取信号量，释放信号量，创建任务等)，并于迹上定义了有限优先级反转以及优先级继承协议.之后，该项目证明了当迹满足协议定义时，其必将满足有限优先级反转性质.然而，这种定义方案严重的限制了该项目的可扩展性：该项目对迹的硬编码使得该方案难以在加入新的接口(如信号量等待超时等)，而这在实际的应用中常常是需要的.此外，该方案中缺乏对语义的描述，这使得该方案难以被用来进行代码层面的验证.

Dutertre[7]通过PVS框架定义了优先级天花板协议并给出了使用此协议时的任务执行时间的上界.该工作使用了模型检测方案，这使得该工作只能被运用在有限任务且有限迹的系统中.此外，该项目对于协议的硬编码也导致了扩展性的缺乏.

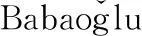
总的来说，相比以前的工作，本文的工作具有以下优点：

1)本文的方案具有较高的可拓展性，可以便捷的对信号量加入新的特性以及API等.

2)本文的方案可以被运用于多种保证有限优先级反转性质的协议中.

3)本文的方案能够用于验证底层的C代码实现的协议.

3 优先级反转的形式化定义

本章会介绍有限优先级反转的形式化定义.同时，由于该性质并不只能由协议本身保证：用户正确的使用协议也是保证该性质发生的一个重要因素，在本章中也会对这部分内容进行形式化的刻画.

3.1 抽象内核模型和优先级反转

一个抽象内核模型必须要实现四种抽象方法：GetCur,GetPrio,GetSemOwner以及GetTaskState.方法GetCur()用于返回抽象内核状态的当前执行任务，方法GetPrio(t)用于取得任务t的优先级.方法GetSemOwner(s)用于返回信号量s的所有者.方法GetTaskState(t)则用来返回任务t的状态.

定义1.优先级反转

状态Σ对于任务t是优先级反转的，当且仅当该状态中任务t的优先级高于正在被调度执行的任务.

3.2 迹和有限优先级反转

由于在操作系统中，往往会使用信号量来控制共享资源，这导致偶尔单次的优先级反转发生本身是不可避免的.本文中真正想要避免出现的问题是优先级反转状态在系统执行过程中出现了无限多次，这种情况被为无限优先级反转(UPI).

为了描绘这种情况，首先引入迹的定义.

ξ:=|||Σ::ξ(coinductive)

为了描述可能存在的无限情形，定义中使用共归纳(coinductive)的方式来定义迹.在该定义中，符号用来描绘迹结束于静默执行(没有新事件生成，但系统依然执行)；符号用于描绘系统正常退出，而符号则用来描绘系统以崩溃的方式结束.

由于无限优先级反转是在表达系统未来的行为.为了便于表达和理解，定义中使用了线性时态逻辑进行表达.关于线性时态逻辑的定义可以参考图3.

图3 线性时态逻辑Fig.3 Linear temporal logic

定义2.无限优先级反转

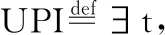
自然地，有限优先级反转的定义可以被定义如下：

定义3.有限优先级反转

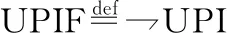
需要注意的是，有限优先级反转的成立与否并不仅仅取决于调度算法及各操作系统接口的实现.该性质与用户对于操作系统接口的正确使用也是息息相关的.

具体的，考虑如下情形：

任务t1和任务t2是两个按优先级从低到高排序的任务.假设在开始阶段系统中只有任务t1在执行.在这时，t1获取了信号量s.之后，任务t2被创建，由于t2优先级高于t1，所以此时系统会切换到t2执行.如果此时t2也需要信号量s，他会被迫等待t1.如果t1永远不释放信号量s，那么这时候t2就会被无限制的阻塞.

在这种情况下，应当认为是用户的错误使用导致了无限优先级反转问题的发生.系统很难处理这种由于用户错误操作导致的问题.实际上，协议在设计时往往假设用户正确的使用了这些系统接口.具体的来说，本文对用户做出以下假设：

1)假设任务获取某信号量后，如果该任务能够执行，那么最终该任务一定会释放该信号量.

2)系统不会发生死锁.

3)信号量的获取与释放是正确的被嵌套使用的.

下面给出这些假设的形式化的定义(定义中出现的辅助定义参考图4)：

定义4.有限临界区假设

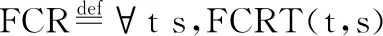
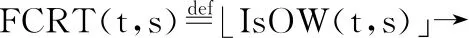
迹符合有限临界区假设成立当且仅当对于任何任务t，如果该任务能被执行，那么它所持有的任意信号量s都最终会被释放.

注意到定义中强调了如果该任务能够被执行，这一点对于用户满足这个假设是非常重要的：用户难以保证任务在不被执行的情况下依然能够释放信号量.

定义5.无死锁假设

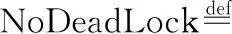
无死锁假设成立当且仅当序列中的所有状态均不存在死锁环(存在某任务直接或间接的等待他自己).

无死锁假设也是必要的，由于当死锁发生时系统实际上难以正确运行，讨论有限优先级反转也就什么意义了.

定义6.正确嵌套假设

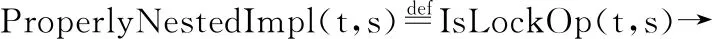
∀s′,⎣IsOW(t,s′)」→。(⎣IsOW(t,s′)」W⎣IsOW(t,s)」)

正确嵌套假设成立当且仅当对任意的任务t和信号量s，如果任务在获得信号量s后获得了s′，那么该任务一定会优先释放信号量s′.

最终，用户需要满足的所有的规范可以定义如下：

定义7.用户正确操作

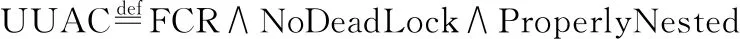
4 高层机器与语言的刻画

由于用户真正关心的是如何证明的是内核代码能否符合有限优先级反转.本章会首先给出一套高层抽象语言的定义，该套语言可以被用来刻画各种优先级反转协议.之后，本章定义了静态代码层面的有限优先级反转——对于任意用户代码，只要用户正确的使用操作系统接口，所有由该系统执行生成出的迹均满足有限优先级反转.

4.1 高层程序

系统抽象代码(P)的定义可参考图5.其由两个部分组成：用户代码A以及内核规范代码O.内核规范代码包括了内核的应用编程接口ρ，中断处理程序Q以及调度器χ.其中，应用编程接口是由函数名到该函数的规范代码的映射.中断处理程序则是一个规范代码的列表，其中列表的第n项代表了该代码是n级中断的处理函数.调度器是内核状态Σ和任务标识符t的关系，用来描绘若在内核状态下进行调度，调度目标将会是t.

规范代码ω一共有6种形式：元语γ在接收一个参数列表后会是两种抽象内核状态之间的关系，他能被用来描述各式各样的协议.sched描述了一个产生调度的语句，而create则用来描述一个创建新任务.ω1;ω2用来描述串行语句，该语句会按照顺序依次执行，ω1+ω2用来表达选择执行语句，机器可以选择其中的任意一条进行执行.end v则用来表达规范代码执行结束，返回值是v.

4.2 高层机器状态

高层状态的定义可以参考图6，高层机器状态Φ包含了程序当前执行Π，客户状态Δ和内核状态Σ.Π是一个由任务标识符到代码执行栈的映射，系统会始终从中取出当前被执行任务的代码片段进行执行.Δ是一个由任务标识符到客户局部内存的映射，代表了客户程序的内存状态.而Σ则代表了内核状态信息，其可以根据需要进行具体的实例化.

图6 抽象状态Fig.6 Abstract state

4.3 语义及迹的生成

为了合理的描绘中断，本文的语义部分定义采用了非确定性的形式.高层机器的中断描绘较为简单：中断可以在任何情况下执行，当中断发生时，系统会立即将中断代码置入当前任务的代码栈中，这样中断处理函数就会立刻响应执行.此外，语义需要记录高层抽象状态随着系统执行的变化，这样就可以得到一个上文提到的所需的迹.

有一个关键的问题是，需要记录哪些系统状态的变化？从应用程序用户的视角来看，所有的系统应用接口的调用都是一个黑箱，并且，系统中断也不在这些用户的考虑范围之内.因此，本文将语义在进行任务步骤时(执行用户代码的步)会输出一个当前内核状态的记录；而在系统步骤中(执行API或中断处理函数期间)不输出这样的状态记录.这样，迹就可以通过记录语义的内核状态输出来得到了.

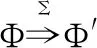
迹的生成被定义为如下形式：

定义8.迹的生成

所有可能生成的迹则通过以下定义得到：

定义9.所有合法迹

其中：

高层系统满足有限优先级反转定义如下：

定义10.高层系统有限优先级反转

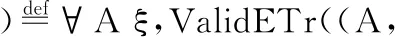
5 在抽象规范层面证明有限优先级反转

之前的章节定义了高层系统上的有限优先级反转，但直接证明这个性质往往是十分困难的.这主要是因为定义涉及到由静态高层抽象规范生成动态的迹.本章会尝试简化证明的思路.参考了之前Gu等人已有的相关工作[10]，本章引入一些单步的性质，并证明这些性质可以推导出高层系统有限优先级反转.通过将复杂的全局问题规约成每一小步的性质，就能够简化许多证明的工作.

回忆图1中描绘的情形，当优先级反转发生时，应该让t1在t2被创建后接着执行.这是由于此时t1阻塞了t3，所以该任务应当被认为具有至少为t3的紧急程度.因此，必须让该任务首先得到执行.这样的需求要求设计出一种新的调度器，该调度器并不能仅仅只根据每个任务的优先级执行任务调度——它还需要考虑任务间的阻塞关系.

所以，一个可能可行的方案就是，让调度器选择的对象要么具有最高优先级，要么阻塞了最高优先级任务的执行.然而，这个要求对于一个一般的防止无限优先级反转的协议太过于严格.实际上，考虑每个临界区均在有限执行时间内被完成时，可以合理地认为调度器只要能够不停地调度到任意一个具有信号量的任务或最高优先级的任务，那么有限优先级反转就可以满足了.

形式化的，可以给出如下的定义：

定义11.合理调度策略

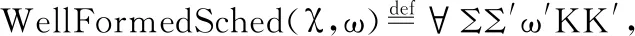
(χ├((ω,K),Σ)→((ω′,K′),Σ′))→

ProperlySched(χ,Σ)→ProperlySched(χ,Σ′)

其中

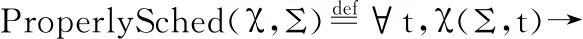
HighestPrio(Σ,t)∨(∃s,Σ.IsOW(t,s))

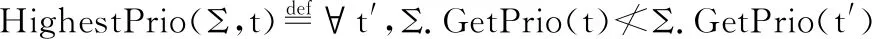
定义中符号_├_|→_用于指代高层语义中的单步内核操作语义.

合理调度策略成立当且仅当对任意初始状态Σ，根据代码ω执行一步后变为状态Σ′时，若性质ProperlySched对Σ成立，则其一定对Σ′成立.

该策略正是之前所说的要求的形式化描述，此外，为了保证调度器确实在合适的时机起到了调度作用，还需要以下两个定义：

定义12.释放信号量后执行调度

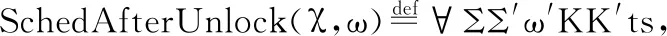
(χ├((ω,K),Σ)((ω′,K′),Σ′))→

Σ.GetSemOwner(s)≠t→HaveSched(ω′)

定义13.创建任务后执行调度

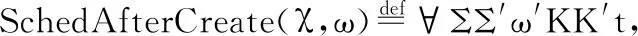
(χ├((ω,K),Σ)→((ω′,K′),Σ′))→

(∀s,Σ.GetSemOwner(s)≠t)→HighestPrio(Σ,t)→

其中HaveSched函数是用来在语法层面表达后续的语句中含有sched语句：

这两个定义表达了在什么情况下操作系统必须要进行重新调度.实际上，只有两种情况可能造成当前执行的任务：1)释放的操作—这会导致阻塞关系的变化，该操作可能导致当前任务不再阻塞某信号量；2)创建的操作—创建新任务可能导致当前任务不再是最高优先级的任务了.当发生这两类操作后，必须要求操作系统重新执行调度.

除此之外，系统接口也需要符合以下规范：

定义14.信号量独立性

(χ├((ω,K),Σ)→((ω′,K′),Σ′))→

定义15.优先级维持

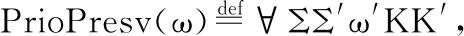
(χ├((ω,K),Σ)→((ω′,K′),Σ′))→

∀t,Σ′.GetPrio(t)=Σ.GetPrio(t)

通常来说，这两个性质是容易保证的.信号量独立性说的是每个任务只能通过自己主动的一个操作来尝试获取一个信号量.需要注意的是该定义并非要求任务必须在自己执行时获得信号量.在一些操作系统实现中，会在释放操作时使另一个任务获得信号量，该操作并不和该定义矛盾—另一个任务必定是由等待状态转为获得信号量的就绪状态.

优先级维持的性质往往也较容易被保证.它要求任务的优先级在执行中不会被改变.需要注意的是该定义所要求保持不变的优先级指的是任务的逻辑优先级.在一些协议的实现中，某些操作会临时调整任务的优先级，但这种调整的优先级并非任务的逻辑优先级，而只是一种临时优先级.

最终，可以汇总得到以下定义及定理：

定义16.合理有限优先级反转系统接口

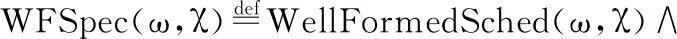
SchedAfterUnlock(χ,ω)∧SchedAfterCreate(χ,ω)∧

WaitIndependent(ω)∧PrioPresv(ω)

其中，suffix是用于在语法上计算可能后续语法的函数：

最后，就能够给出本章最重要的一个定理：合理OS实现可以推导出有限优先级反转.鉴于该定理的证明过程较为繁琐，具体证明部分可以参考具体Coq代码中的证明部分.

定理1.合理OS实现蕴含有限优先级反转

∀O,WellFormedOS(O)→HOSFUPI(O)

6 底层有限优先级反转

至此，本文已经展示了如何在协议规范层面证明有限优先级反转的方案.但这仍然与本文的最终目标—在实际的机器层面进行验证存在差距.本章会介绍一套方案来用于解决这个问题.首先，为了能够表达底层机器模型，下面先各处底层机器模型的定义.

6.1 底层机器及语言

图7给出了本文中底层程序和状态的定义.这部分定义主要参考了x86体系结构.定义中，P是底层的程序，其中A是已经在之前提到过的客户端代码，O是底层的系统代码.Φ则是底层的系统状态，与高层类似，它包括了任务代码执行栈映射Π和用户程序状态映射Δ.除此之外，其还包含了底层的系统状态σ.

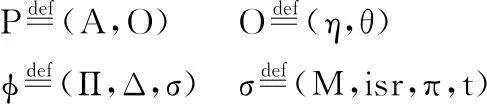
图7 底层程序和状态Fig.7 Concrete program and state

虽然大多数的操作系统都是由C语言和汇编来实现的，但完整的刻画这些语义过于繁琐并且没有必要.这是由于实际上在操作系统实现中所用到的汇编只有很特定的一部分.作为替代方案，本文将操作系统中常用的汇编代码块分别抽象为了汇编原语，与标准的C语言一起用作本文的底层语言(见图8).

图8 底层语法Fig.8 Concrete syntactic

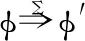
迹的生成的定义类似于高层语言：

定义17.底层迹生成

定义18.底层合法迹

6.2 底层有限优先级反转

底层有限优先级反转的定义也与高层类似：

定义19.底层系统有限优先级反转

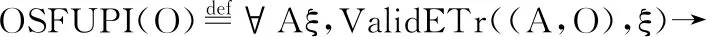
6.3 精化关系

由于本文在之前已经在协议规范层面证明了有限优先级反转性质，所以现在的问题可以归结为如何证明一个具体实现的协议代码确实是一个正确的规范实现.为此，定义如下的精化关系：

定义20.精化关系

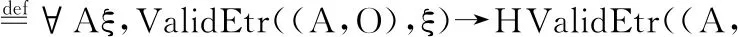
精化关系描绘了底层的所有可能生成迹与高层所有可能生成迹之间的子集关系.借此表达底层的具体协议代码必然是一个合理的高层协议规范的实现——因为该底层系统所有可能行为均可被高层规范认可.

由精化关系和有限优先级反转定义，可以得到以下定理.

定理2.精化关系维持有限优先级反转

∀OO,HOSFUPI(O)→O⊆O→OSFUPI(O)

6.4 CSL风格的关系程序逻辑

精化关系在验证底层的有限优先级反转问题中有很大的作用.然而，证明具体高层代码与底层代码见的精化关系并不容易.这主要是由于并行程序的非确定性语义导致的.本文参考Liang等人[11,12]中的逻辑，设计给出了用于本文所需的逻辑.该逻辑基于将分离逻辑(CSL)运用于并行系统中，能够较好的支持并行程序的验证需求.然而，由于逻辑整体较为复杂而且繁琐，限于篇幅的限制，在此从略.

6.5 逻辑可靠性

定理3.逻辑可靠性

∀OO,├ O:O→O⊆O

定理中符号├ O:O即用于表达底层实现与高层规范间符合本文的程序逻辑.逻辑可靠性定理保证了逻辑能够推理出两层间的精化关系.证明这个定理并不简单，本文根据Liang等人[11,12]中提出的思路将基于RGSim-T证明逻辑可靠性的方案延拓到多任务模型中来证明了这个定理.

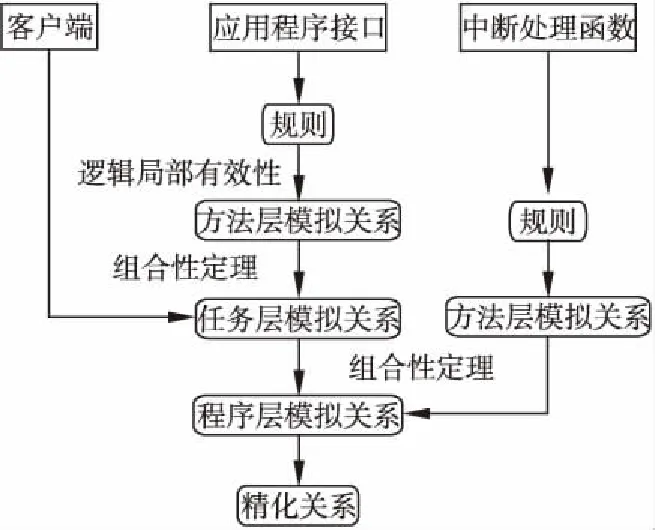
图9 逻辑有效性证明框架Fig.9 Soundness proof structure

本文展示了该定理的证明框架(见图9).为了证明逻辑可靠性，本文定义了3层模拟关系.并通过可组合性定理建立最终的程序层模拟关系，最终可以得到精化关系.

7 验证POSIX标准协议

本章会采取上述方法来验证POSIX标准中给出的两种避免无限优先级反转的协议.这两个协议被称为“优先级保护协议”(PPP)和“优先级继承协议”(PIP).

7.1 抽象内核状态实现

图10给出了本章使用的高层抽象系统状态的实例.状态Σ包含了任务池T，信号量集合S和当前执行的任务标识符tc.T将每个任务标识符映射到一个包含了任务逻辑优先级，任务状态及被用于调度的任务当前优先级的三元组.S则将每个信号量标识符映射到一个由状态和优先级组成的二元组.这其中优先级是优先级保护协议中所需要用到的域.

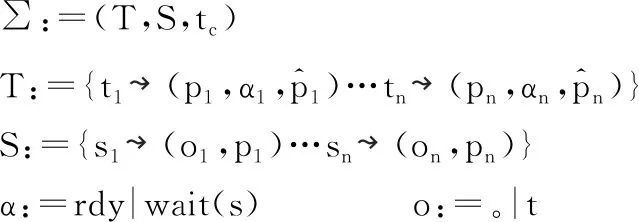
图10 抽象系统状态实例Fig.10 Abstract kernel state

7.2 优先级保护协议规范

优先级保护协议会赋予每个信号量一个优先级，并且只允许那些当前优先级低于信号量优先级的任务申请使用该信号量.当任务获得某信号时，系统会临时将该任务的优先级提高到信号量的优先级.并在释放信号量时恢复优先级.形式化的优先级保护协议的定义可以参考图11.

图11 优先级保护协议形式化定义Fig.11 Formal definition of PPP

规范ρPPP包括了两个API—lock与unlock.定义中，χhp是根据临时优先级进行调度的调度器.原语γlocksucc描述了信号量被成功获得的情形，并且会造成之前所说过的任务优先级提升.γlockerr则描述了任务尝试获取信号量时出错的情况.在释放操作的定义中，γPPPunlock1描述了释放信号量时降低任务优先级的行为.γunlockerr则描述了释放信号量发生错误的情形.限于篇幅，本文省略了定义中一些较为繁琐的部分，其大致含义可以参考之前介绍的协议内容.

运用定理1，可以证明以下定理.

定理4.优先级保护协议保证有限优先级反转成立

HOSFUPI(OPPP)

7.3 优先级继承协议规范

当系统采用优先级继承协议时，如果一个低优先级的任务阻塞了一个高优先级的任务，系统会在其阻塞期间将该任务的优先级调至高优先级.形式化的定义可参见图12.

与优先级保护协议类似，可以证明得到以下定理：

定理5.优先级保护协议保证有限优先级反转成立

HOSFUPI(OPIP)

7.4 精化关系证明

最后，本文用C语言实现了这两个协议(OPPP和OPIP).通过运用第6章中的逻辑和定理2，得到以下两个定理：

定理6.C语言版本的优先级保护协议能保证有限优先级反转

OSFUPI(OPPP)

定理7.C语言版本的优先级继承协议能保证有限优先级反转

OSFUPI(OPIP)

至此，本文完整的证明了底层实现的协议能够满足有限优先级反转的要求.

图12 优先级继承协议形式化定义Fig.12 Formal definition of PIP

8 总 结

本文给出了一套较为完整的方案用于验证操作系统中有限优先级反转的方案.对比已有的工作，本文所介绍的方法的可扩展性更强，应用面也更广.并且，这是第一个能够在具体代码的实现层面上验证该性质的方案.本文通过Coq实现了所有文中提到的定理与定义，这也确保了证明过程的正确性.

但同时，基于Coq的代码证明任务十分的繁重.这一方面是由于使用Coq定理证明工具在验证实际问题时所必须要面临的局面.一方面也是由于现有的自动化策略与定理库的支持不足.在这几点上还需要更多的改善和进步.