动态时间规整算法优化

叶科淮，陈 志，王仁杰，史佳成，胡 宸

（1.南京邮电大学 计算机学院、软件学院、网络空间安全学院，江苏南京 210023；2.南京邮电大学 通信与信息工程学院，江苏 南京 210003）

0 引言

时间序列数据在生活中随处可见，时间序列数据本质上反映的是某个或某些随机变量随时间不断变化的趋势。目前时间序列相似性度量常用方法是动态时间归整（Dy⁃namic Time Warping，DTW）算法，文献［1］证明出DTW 算法比欧几里得距离搜索算法更有效率，但该算法时间序列长度较长，两段时间序列长度相当时计算效率较低。本文通过分析现有DTW 算法优化方法，对算法进行扩展和改进。

DTW 基于动态规划（Dynamic Programming，DP）的思想，具有较高的时间复杂度且对噪声敏感，传统DTW 时间复杂度为O（mn），其中m、n 为时间序列长度。DTW 算法有很多变种，如多变量动态时间规整MDTW［2］、测量索引距离的IDTW［3］、可以解决传统DTW 奇异问题的DDTW［4］及WDTW 算法［5］等。

为提高DTW 度量效果，众多学者进行了相关研究。Salvador 等［6］提出的FastDTW 算法在粗粒度空间内执行DTW 算法，将复杂度优化至O（n），该算法在数据量极大的情况下十分有效，但是在求取DTW 距离时会产生较大误差；分块算法可优化效率，如对时间序列进行分块［7］、对动态规划产生的矩阵进行分块［8］等，但是也会带来一定误差；褚蓉等［9］提出一种基于形状与升降性提取序列数据重要特征点的DTW 相似性搜索算法，解决了分块带来的特征丢失问题；文献［10］展示了通过全局变量约束，限制搜索区域可行性；针对全局约束以减少计算时间的方法主要有Sakoe-Chiba 约束［11］与Itakura-Parallelogram 约束［12］；文献［13］根据后者应用情景，将全局约束范围由平行四边形转变为动态平行四边形；文献［14］证明Sakoe-Chiba 约束在弯曲限制为r 时只适用于n-r≤m≤n+r的情形。本文对Sakoe-Chiba 约束进行拓展，扩充其应用范围。

本文对DTW 算法进行扩展和改进，将该优化方法应用于较长的时间序列进行试验。结果表明，该方法在两个时间序列相差不大时能将时间复杂度降低至线性，并可以准确判断时间序列是否相同。

1 传统DTW 算法

设参考模板为R={R1,R2,R3,…,Rn}，测试 模板为T={T1,T2,T3,…,Tm}，其中参考模板共包含n帧，测试模板共包含m帧，Ri、Tj分别表示参考模板的第i帧和测试模板的第j帧特征矢量。

参考模板与特征模板的失真度决定了两个序列相似度，失真度越小，则相似度越高。测试模板第i帧Ti与参考模板第j帧Rj的失真度为d(i,j)，设D(i,j)为测试模板匹配了i帧、参考模板匹配了j帧失真度。为了求取最终答案D(m,n)，可以定义1 个矩阵，矩阵的(i,j)位置包含d(i,j)和D(i,j)。

对于规整路径W={w1,w2,w3,…,wk}，有：

其中W的约束条件有：

（1）规整路径满足w1=(1,1)，且wk=(m,n)。

（2）对于任意的1≤i＜k，当wi=(ai,bi)，wi+1=(ai+1,bi+1)时，有ai+1≤ai+1 且bi+1≤bi+1。

（3）对于任意的1≤i＜k，当wi=(ai,bi)，wi+1=(ai+1,bi+1)时，有ai+1≥ai，bi+1≥bi，且ai+bi≠ai+1+bi+1。

基于以上约束条件，通过动态规划的方法，得出状态转移方程为：

在矩阵中通过该转移方程得到的是一条从(1,1)走到(m,n)的路径，约束条件限定了每一步只能从(i,j)走到(i+1,j)，(i,j+1)或(i+1,j+1)，规整路径是所有路径中满足经过格点的∑d(i,j)最小的一条。

2 优化方法

传统DTW 算法需在对任意1≤i≤m，1≤j≤n都求出D(i,j)值后，才能得到最终答案D(m,n)。设DTW 算法计算次数为NM，实际上，该算法对每一对可能比对的帧均进行比较。

2.1 时间序列压缩

应用传统DTW 算法对两个时间序列进行比较，最终得到的匹配结果是通过对模板T 和R 进行伸缩和拉伸后的时间序列。在实际应用中，如语音序列相似度计算，对参考模板的改变并没有实际意义，所以可令参考模板不变，只将测试模板向参考模板的方向进行变化即可。

在参考模板和测试模板的界限比较模糊时，易知参考模板与测试模板可互换，求得的结果相等，所以可令序列长度较短的模板为参考模板T，较长的模板为测试模板R，因为有m≤n，所以应对R 进行收缩。

2.2 全局约束条件添加

在传统约束条件之外，有时候关键路径还需要满足全局约束条件，即任意一条关键路径中的每一个点（i，j）需要满足全局路径中的要求。这样，对于不满足约束条件中的所有点，在计算D（i，j）时可在不影响后续点的情况下忽略。

在Sakoe-Chiba 约束［11］中，关键路径的可能点是一条主对角线方向上的带形。根据DTW 算法的状态转移方程，在带形之外所有状态失真度均不会作为格点之内的状态失真度计算的前提，所以仅计算带形之内的状态失真度即可，约束范围如图1 所示。

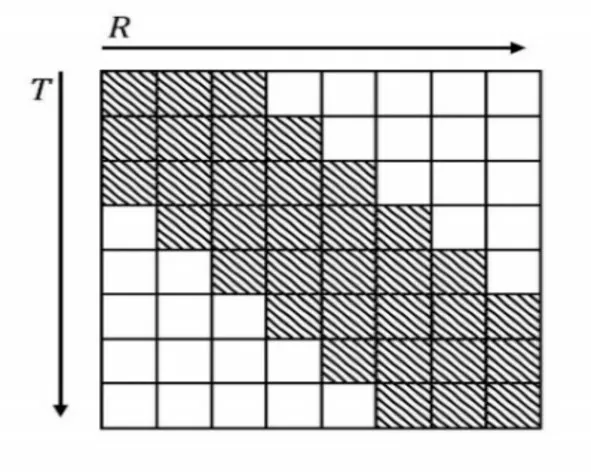
Fig.1 Sakoe-Chinba restriction图1 Sakoe-Chiba 约束

设这种全局约数限制为r，则对于所有1≤j≤n，阴影部分所有状态(i,j)均需满足j-r≤i≤j+r［14］，所以使用Sakoe-Chiba 约束必须有m-n≥r，即对不等长序列长度差具有一定限制。

为了尽可能地克服这种限制，本文将阴影区域划分为状态(1,r)边界中点与状态(m-r+1,n)右边界中点的连线、状态(r,1)左边界中点与状态(m,n-r+1)右边界中点状态连线与全局边界围成的部分，如图2 所示。

Fig.2 Improved restriction when r=2图2 改进后r=2 时的约束

改进后Sakoe-Chiba 约束可普遍应用于求DTW 距离的场景，即使是两个时间序列相差比较大的情况。设置全局约束可优化DTW 计算时间，基于该思想，本文对规整路径W 的约束条件进行改进，使改进后的DTW 算法在一些特殊的应用环境中可达到更高效率。

2.3 特殊情况下的改进

上述优化虽然一定程度上减少了算法计算时间，但是在比较两段包含相同内容的时间序列时，仍有改进空间。针对两段内容相同的时间序列，如果一段时间序列是另一段时间序列部分压缩的结果，使用这种改进方法可以得到很好的反馈。

在2.1 章节的前提下，假设新的约束条件：

（1）规整路径满足w1=(1,1)，且wk=(m,n)。由于R不变，反映到图像上，规整路径方向只有从(i,j)到(i,j+1)与(ι+1,j+1)，所以可得出k=max(n,m)=n。

（2）对于任意1≤i＜k，当wi=(ai,bi)，wi+1=(ai+1,bi+1)时，有ai≤ai+1≤ai+1 且bi+1=bi+1。在原约束条件的基础上整合单调性与连续性，并由性质给出更加精确的条件bi+1=bi+1。

基于以上约束条件，每个点(i,j)能转移到的地方为(i,j+1)或(i+1,j+1)，可以看出无论(i,j)向哪个方向转移，纵坐标j都增加了1，所以规整路径的长度一定为n。并且由于规整路径是从(1,1)到(m,n)的路径，所以转移到(i+1,j+1)的次数恒为m-1。

为了求出最终答案D(m,n)并尽可能多地减少不必要运算，在[1,m]×[1,n]的矩阵中，所有不可能通过前文所述的两条约束条件走到(m,n)的点均无需计算。

矩阵中的任意点(i,j)，根据纵坐标的约束条件，走到(m,n)需要n-j步，在每一步中同时需要横坐标增加m-i次，所以有：

同时，这个点还要满足可以从起点（1，1）转移过来，即：

所有满足上述两式的点，都不需要在动态规划的过程中计算出来，因此可以省去大部分计算时间。通过线性规划的方法，可以得到规整路径可能经过的地方，也就是需要计算D(i,j)的点，如图3 所示。当n=m时，计算次数仅有n次，此时关键路径W={(i,i)|i=1,2,3,…n}。

Fig.3 Points to be calculated for warping path图3 规整路径需要计算的点

经过这种在特殊情况下的优化，需要计算的D(i,j)状态有n(m-n+1)个，而原算法计算的数量为nm个，即改进算法可以比传统算法少计算n(n+1)次。因此可以得出结论，改进算法的复杂度为O(n(m-n))，当n越大，改进算法的优势越大，又因为n≤m，所以当n与m越接近时，算法效率越高。

3 实验数据分析

3.1 随机数据下的实验

将改进的时间序列相似度计算算法与传统DTW 算法进行比较，为了使任意两帧的失真度d(i,j)可由O(1)求出，随机生成两个正整数数组T、R，并令d(i,j)=(Ti-Rj)2。在相同的实验环境与数据集中，分别运行两个算法，同时记录两个程序运行中消耗的CPU 时间。对每组实验结果进行对比，并且分析在不同模板长度下对时间序列进行计算的改进效果。得出的数据如表1 所示。

Table 1 Test results of random data表1 随机数据实验结果

通过表1 的数据可以看出，两种算法在数据量比较少的情况下运行时间均较短，看不出明显差异。为了对比参考模板长度与测试模板长度关系对算法改进效率的影响，假设测试模板长度不变，实验效果如图4 所示。

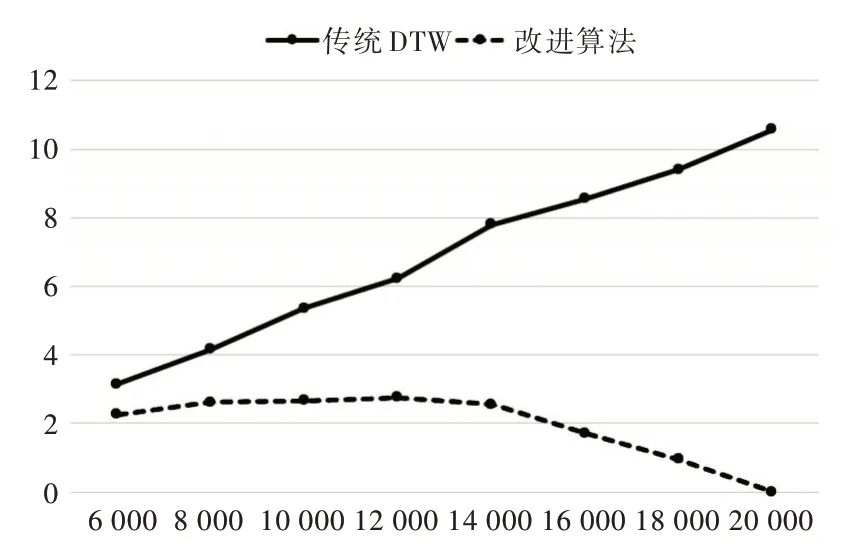
Fig.4 Efficiency comparison when m=20 000图4 当m=20 000 时的效率对比

横轴代表n 的长度，纵轴是算法运行时间，单位为秒。如图4 可知，在数据量比较大的情况下，当测试模板与参考模板长度差异较大时，如表1 的第4 组实验，提高了39.5% 的效率；而参考模板长度约接近测试模板，如表1 第3 组实验，提高了约99% 的效率。

3.2 时间序列内容判断

就视频来说，两段内容相同的视频只可能是播放速率不同，在时间序列上的体现是某些帧重复了多次，如果使用2.3 章节中的改进方法，相同视频得到的失真度应该为无穷小。随机产生一些参考模板，并且选取若干帧进行左右重复扩展，将处理好的时间序列作为测试模板进行实验，结果如表2 所示。

Table 2 Test results表2 实验结果

经过观察可以发现，表2 得出的实验结果与2.3 章节得出的结论一致：当参考模板长度n越大，算法运行时间越短。实验数据中算法运行时间符合改进算法O(n(m-n))的复杂度，并且当两段时间序列相同时，得到的DTW 失真度为无穷小，符合实验前的预测。

4 结语

本文在现有约束前提下，增加及改变了一些约束，提出了一种在时间序列规整过程中压缩时间序列的思想。针对现有他人研究，扩展了Sakoe-Chiba 约束，解决了该约束不能应用于两个模板长度差距过大的问题。根据扩展Sakoe-Chiba 约束设置全局变量的思想，改进了DTW 的前提约束，改进后DTW 算法在识别时间序列时，能在保证高准确度的情况下高效应用。因此该算法可为依赖于实时性的识别匹配系统提供一定帮助，减少硬件开销。

改进后的DTW 算法虽然高效但对应用环境有严格的要求，对除了识别时间序列内容之外的问题不能保证准确性，还待进一步优化与研究。