采用自抗扰技术的移动式增氧机路径跟踪控制

盛 亮，赵德安，孙月平，周文全，潘望俊

（1.江苏大学 电气信息工程学院，江苏 镇江 212013；2.常州市金坛区水产技术指导站，江苏 常州 213299）

0 引言

随着社会的发展，人民生活水平不断提高，河蟹的消费需求也逐年增加［1］。在河蟹大面积养殖过程中，传统增氧方式效率极其有限，可能在增氧机固定地点出现增氧过度、在远离增氧机的地点出现增氧不及时的情况。因此对移动式增氧机进行研究经济意义重大，其中移动式增氧机轨迹跟踪控制是关键［2］。

解决轨迹跟踪偏差问题的常用方法是视线法（Lineof-Sight，LoS）。该方法缺点是水流及风向的干扰会引起移动式增氧机横向速度及漂角变化，不利于控制。纵观相关国内外研究文献可知，常用控制策略有先进PID 控制、最优控制等一些线性控制方法，以及自适应控制、滑模变结构控制、反演控制、模糊控制等非线性控制策略［3-5］。文献［3］采用扩张状态观测器实时估计系统干扰与不确定性，用一种非奇异端滑模算法改进传统自抗扰控制器，得出精确的移动机器人偏航角，实现目标精确跟踪，但所选用的非奇异终端滑模控制律仍没解决移动机器人轨迹跟踪快速性问题；文献［4］将线性最优法与滑模变结构控制方法进行对比，在低速和高速情况下对移动机器人进行轨迹跟踪控制，提出的滑模变结构控制器可提高控制精度与鲁棒性；文献［5］提出一种抗饱和自适应滑模变结构控制方法，以消除参数摄动和不确定因素对控制性能的影响，解决移动机器人鲁棒轨迹跟踪问题，但自适应律计算复杂。

PID 控制器已有近百年历史。因PID 控制结构简单、对模型误差具有鲁棒性及易于操作的优点，自1940 年以来，PID 控制策略与众多控制方法结合，广泛应用于工业领域。如自抗扰控制方法，韩京清［6］于1998 年首次提出自抗扰控制，并指出传统PID 控制不足之处。利用现代控制技术充分发挥PID 控制优势，使其逐渐发展为可代替传统PID 控制技术的理想选择。

自抗扰控制由跟踪微分器（Tracking Differentiator，TD）、扩张状态观测器（Extended State Observer，ESO）和非线性状态误差反馈控制律（Nonlinear State Error Feedback，NLSEF）3 部分组成，扩张状态观测器将系统外部扰动和内部扰动统一视为总扰动，然后对总扰动进行实时估计与补偿［7］。本文运用扩张状态观测器（Extended State Observer，ESO）将移动机器人运动过程中各种干扰扩张出来作为1个新系统变量，并视为系统“总扰动”变量，然后反馈补偿到控制器端进行补偿控制。自抗扰技术可以解决耦合、时变、非线性等一系列问题。本文提出一种基于自抗扰技术的移动式增氧机路径跟踪控制，使移动式增氧机航向控制过程快速、平滑，可使高精度移动式增氧机航向保持控制，增强控制鲁棒性、改善控制动态品质和稳态精度。

1 移动式增氧机结构及工作原理

1.1 移动式增氧机结构

移动式增氧机主体主要包括：主控箱（用于存放主控板、电池等）、工作台（用于固定GPS 箱）、浮体（两个）、明轮（4 个，船体左、右各两个）、船体连接固定板（1 个）、驱动电动机（左、右各两个）、GPS 定位设备等，如图1 所示。其他设备还包括无线通信设备、GPRS、地磁传感器等。

移动式增氧机依靠4 个明轮向不同方向转动，实现移动式增氧机运动及增氧。

1.2 移动式增氧机工作原理

当电机驱动4 个明轮一致向前转动时，移动式增氧机向前运动，在前进过程中，移动式增氧机可将溶解氧浓度高的水推向四周，达到全池塘、全水域遍历式增氧。当电机驱动前后两对明轮向相反方向运动时，此时移动式增氧机可实现原地增氧，在原地增氧过程中，将空气中的氧气压入水中，增加水中溶解氧浓度，并将高浓度的水推向远方，促进水体流动。

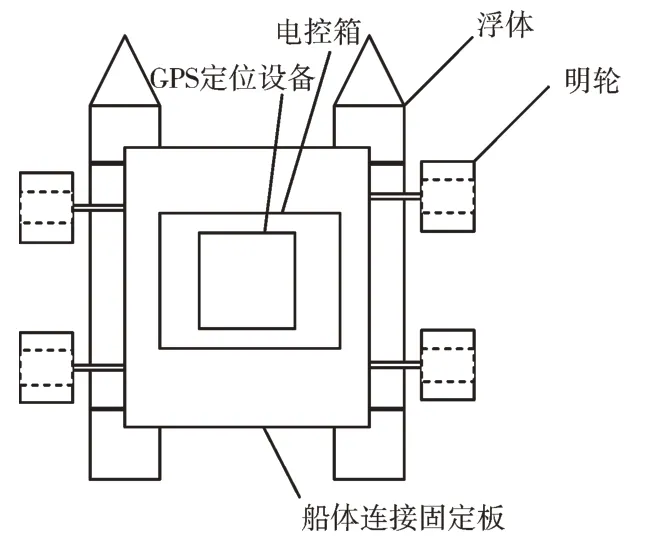
Fig.1 Mobile aerator structure图1 移动式增氧机结构

移动式增氧机通过GPS 定位设备采集实时位置信息，通过设备箱蓝牙传送到主控箱内的ARM 控制板。通过Keil5 编写的单片机程序驱动移动式增氧机电机，利用GPRS 与安卓APP 互连，此时移动式增氧机可通过APP 进行控制。移动式增氧机采用单点增氧与遍历式增氧结合的方式，将溶解氧浓度高的水推向溶解氧低的地方，对池塘各方位进行增氧。

2 路径跟踪误差动力学模型

针对移动式增氧机的运动特性进行分析，建立移动式增氧机运动仿真模型［8］。用于移动式增氧机的路径跟踪Serret-Frenet 运动坐标如图2 所示。

Fig.2 Mobile aerator coordinate system图2 移动式增氧机运动坐标系统

框架｛SF｝原点位于曲线Ω上距离固定框架｛B｝原点最近的点［9］。Ω为给定的目标路径，e为｛SF｝原点到｛B｝的距离，ψSF为路径切向方向，ψ是移动式增氧机航向角［10］。Serret-Frenet 坐标系中路径跟随误差的动力学表达式为：

然后可得到误差动态为：

欠驱动路径跟踪研究中应用最广泛的动力学模型包括：

其中，mii＞0(i=1,2,3)为移动式增氧机给出的惯性以及附加质量的影响。dii＞0(i=1,2,3)为水动力阻尼。可用的控制系统由水动力u1与明轮偏航力矩u2组成，满足u2=b1δ，b1是舵系数。d为模型不确定性的集总扰动和外部扰动，假设满足。由于水流速度为常数，可得到降阶线性模型为：

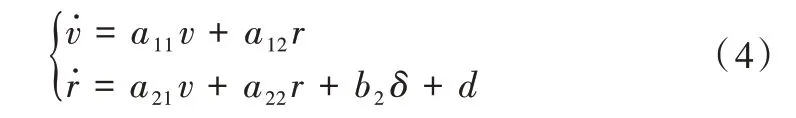
其中，a11、a12、a21、a22以及b2为常数参数，明轮偏航角为等效微分控制输出。因为移动式增氧机同时要求船速慢且明轮转速快，这样才能高效增氧，所以横摇速度v以及其他变量相比足够小。在式（1）中可被忽略，即，此时移动式增氧机前进速度为U=。因此，可如式（5）［12］进行简化。

将欧拉离散化应用于式（5）中，得到离散时间模型［13］，如式（6）所示。

3 ADRC 控制器

自抗扰控制方法利用扩张观测器实现系统扩张状态的估计，它不依赖系统模型并具有很强的鲁棒性，二阶自抗扰控制基本结构如图3 所示。

Fig.3 Mobile aerator coordinate system图3 移动式增氧机航向控制系统

根据前点与目标点之间的距离，将移动式增氧机目标航向、航速信息也送入控制器，经运算后生成明轮控制信号，分别送入对应的控制信号［14-16］。

利用二阶跟踪微分器优化移动式增氧机航向过渡过程，目的是跟踪输入信号与输入信号微分信号［17］。

二阶跟踪微分器离散算法为：

fhan 函数算法公式为：

其中，fhan 函数为最速控制综合函数，d、d0、y、a0、a为fhan 函数内部变量，v为移动式增氧机给定航向，v1实现对v快速无调跟踪，v2为v的微分信号，r、h 为跟踪微分器所需参数［18］。

通过观测得到输出信号与被控对象输入信号，利用扩张状态观测器确定移动式增氧机内部信息，其中扩张状态观测器离散算法［19］为：

非线性函数fal 表达式为：

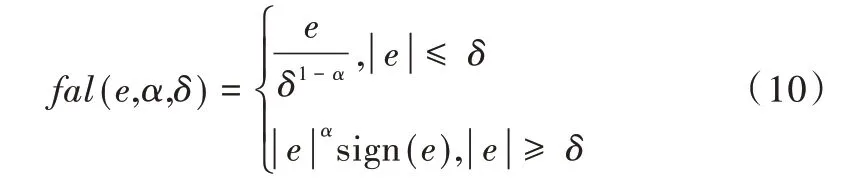
其中，z1为估计跟踪到的移动式增氧机实际航向，z2为估计跟踪到的移动式增氧机实际航向变化率，z3为移动式增氧机航向扰动估计值，e为估计跟踪到的实际航向与实际航向之间误差，β01、β02、β03、b0、δ为扩张观测器需设定的参数［20］。

自扰动技术非线性状态反馈控制率的非线性状态误差反馈控制量如式（10）所示。

其中，e0=v1-z1为跟踪过程与观测器间的误差信号，为误差积分信号，e2=v2-z2为误差微分信号［21］。

4 仿真及实验结果分析

对移动式增氧机航向角、距离分别进行仿真测试，仿真MATLAB 结构如图3 所示。模拟移动式增氧机在风、水流等干扰下存在扰动项，模拟移动式增氧机受到外力干扰。基于移动式增氧机坐标系统进行仿真，以此说明ADRC 可行性及有效性。根据此时实验移动式增氧机尺寸可计算出a22=0.056 22，b2=0.000 761 3。所以，A1=，A2=[1 7.745 0010.5001.0281]，。此次采用的干扰为d(t)=sin(0.5t)。初始状态为：[x1(1)x2(1)x3(1)]=[15-5 0],[0 0 0]，并且|δ|≤35°。

图4 为移动式增氧机中总扰动ESO 估计，在伴随有外界干扰d（t）的状况下，会出现较大的耦合项。

Fig.4 Interference estimation图4 干扰估计

距离误差及航向角误差仿真如图5、图6 所示。从图5 可以看出，ADRC 控制方法的曲线较PID 方法更加平稳，稳定误差较小，跟踪精度良好。从图6 可以看出，ADRC 控制方法更加迅速地达到稳定状态，并且稳定误差小于PID控制方法。可见本文提出的自抗扰控制满足控制约束，对干扰具有较强的鲁棒性。在自抗扰控制方法下，移动式增氧机在30s 后距离误差仅0.2m，航向角误差0.1°，PID 控制下的距离误差有2m，航向角误差为0.5°。因此本文提出的ADRC 控制性能符合要求。

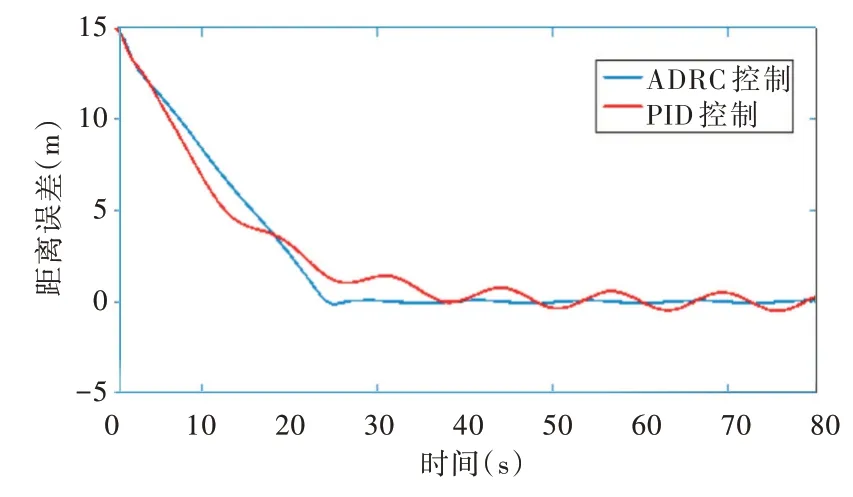
Fig.5 Distance error图5 距离误差

Fig.6 Heading angle error图6 航向角误差

5 结语

本文提出了基于自抗扰技术的移动式增氧机路径跟踪控制，仿真结果显示该自抗扰技术在外部干扰下与预估干扰大致符合要求，并在外部干扰下自抗扰技术距离误差及航向角控制效果理想。在传统PID 控制下，移动式增氧机30s 后距离误差有2m，航向角误差有0.5°；在自抗扰控制方法下，移动式增氧机在30s 后距离误差仅0.2m，航向角误差0.1°。因此可以得出结论，采用自抗扰技术的移动式增氧机可克服干扰的影响。

虽然本文对移动式增氧机航向及距离误差进行了预测，但应用的是单目标优化方法，即将所有限制条件加权组合成适应度函数，这种策略不是最优的。后续研究将聚焦于控制器参数优化，以期得到性能更佳的多目标优化算法，对移动式增氧机轨迹跟踪进行精确估计。