蚁群算法在高阶时滞系统频域辨识中的优化

（上海理工大学光电信息与计算机工程学院，上海 200093）

0 引言

工业生产过程中，要想良好的控制被控对象，首先要确定被控对象模型，但工业过程如伺服电机控制系统、炉内脱硫系统等往往会产生一些非线性、复杂、高阶的［1-3］时滞对象。而工业控制中最重要的控制器就是PID 控制器［4］，但对于高阶时滞系统的PID 参数设计非常繁琐。为了方便控制器设计，需以低阶简易的模型进行拟合。系统辨识是工业建模中的常用方法，一般先选取合适的传递函数模型，然后加上激励信号，通过分析系统输入输出特性，采用一定的辨识方法得到对象的等价模型［5］。

传统的辨识方法主要有极大似然法、频域响应法、最小二乘法。工业生产对于辨识高阶系统所采用的模型，主要以基于最小二乘法的一阶时滞模型［6-8］和基于1/1Pade逼近的二阶模型［9］为主。由于对象的复杂性，实际应用这些方法会与原系统存在较大误差，并且在拟合精度上较差。为了提高模型拟合精度，Wang 等［10］提出了一种通过对信号进行分解，选取10 个频率点来拟合二阶纯滞后模型的闭环辨识方法，该方法对于一些强耦合、大时滞的复杂对象具有很好的辨识效果；文献［11］采用二阶时滞模型对含积分环节的对象进行辨识；文献［12］利用频域分析及选点，通过二阶时滞模型对含微分环节的对象进行辨识；文献［13］通过二阶时滞模型对具有振荡特性或者非振荡特性的高阶时滞模型进行辨识。这些学者的实验均验证了二阶时滞模型的优越性，但他们的研究均是在重要频率段内随机选取一定数量的频率响应点，由于选点的随机性及选点个数的局限性，模型参数的精度仍有很大提升空间。

本文提出采用蚁群算法实现高阶时滞系统辨识优化，是在二阶时滞模型基础上，充分利用蚁群算法的特点，通过寻优适应度函数极小值，找到在重要频率段内的最佳频率响应点，即通过较少的频率响应点，求出二阶时滞模型的各参数，利用MATLAB 仿真并与传统工业方法作比较。通过结果可知，本文方法得出的幅频特性曲线与原曲线拟合程度更高。

1 对象的频域建模方法

1.1 频率响应特性

控制系统中的信号经常出现从一个稳定状态变化到另一个稳定状态的情况，两个稳定状态变化过程中包含了极为重要的频域特性［14］。一般的系统响应信号f（t）是由瞬态部分Δf(t)和稳态部分fs(t)组成，如式（1）所示。

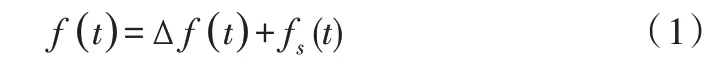
由于两个稳定状态之间的变化信号通常不满足绝对可积条件，考虑对等式两边进行Laplace 变换，得到式（2）。

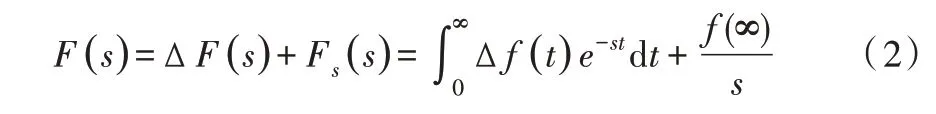
若系统输出信号在t=Tf时刻达到稳定状态，此时瞬态响应Δf(t)的值为0，由式（2）可得式（3）。

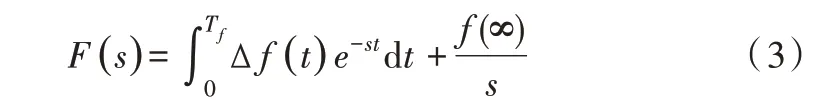
控制系统的输入信号和输出信号可由式（3）近似得出当前工作点的传递函数。

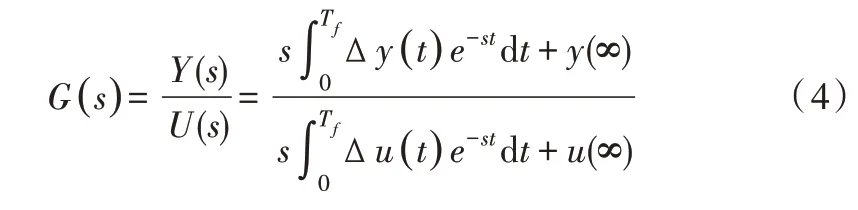
若系统对象输入为阶跃信号时，∆u(t)值为0，输出则为瞬态和稳态两个部分。令s=jω，由式（4）可得式（5）。

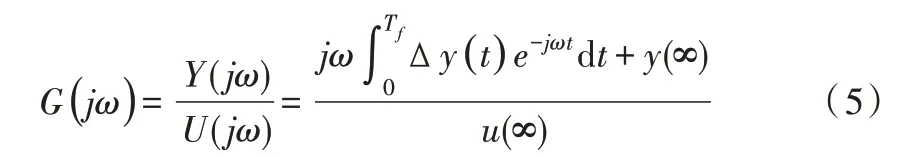
将式（5）的积分部分分成N 个长度为Δtk的子区间，展开成积分累加的形式，如式（6）所示。

其中，Nf为数据的采样个数。

在式（6）的基础上，进一步推导整理，得到对象各重要频率点的频率响应特性。

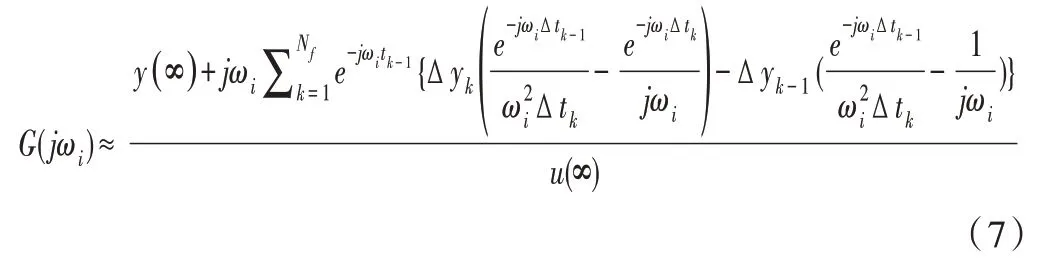
这样对于任意给定频率ω，都可根据式（7）求出该频率点时对象的幅值和相位。

1.2 重要频率段确定

假设对象模型收敛，由于系统稳定性主要由中低频段决定，而高频段几乎不影响系统的稳定，所以重要频率段位于Nyquist 图的第二、三象限，即从零开始到对象的临界频率点是其重要的频域范围。构建弦截迭代公式如式（8）所示［15］。

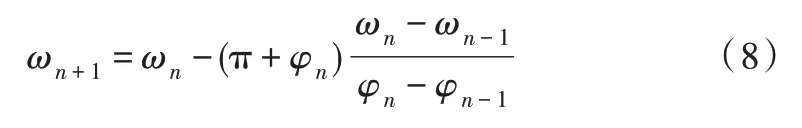
相角与频率间的函数关系如式（9）所示。

初值ω0和φ0均为零，ω1取一个极小的数，例如0.000 01；其中G(jωn)可由式（7）得到，φ1通过式（9）计算得到。经过数次的反复迭代后，可以求出对象的临界频率ωc（对应相角为-180°），则（0，ωc）为确定的重要频率段。

1.3 传递函数模型

实际生产过程中的工业控制非常复杂，文中采用具有任意极点的二阶时滞模型去拟合高阶时滞对象，传递函数模型如式（10）所示。

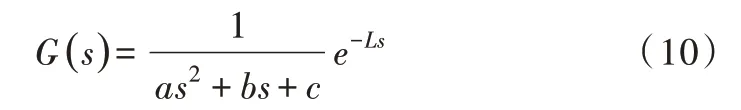
其参数是在重要频率段内选取多个频率响应点，本文利用蚁群算法，在重要频率段内通过选取5 个较优点求取，再通过幅值和相角关系拟合此模型。幅值关系如式（11）所示。

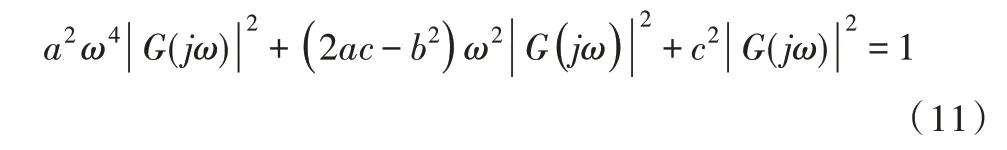
可用矩阵表示如式（12）所示。

其中：

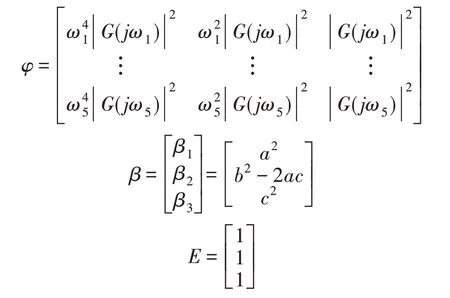
根据线性最小二乘法式（13）：

从而得到式（14）。

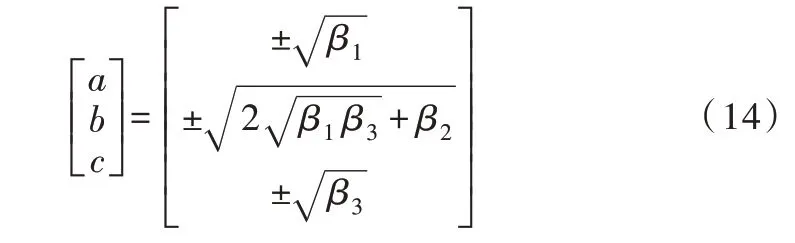
可求得参数a、b、c，若对象的输出随着系统输入增加而增加，则参数值取正，反之取负。相角关系如式（15）所示。

同样采用最小二乘法求出参数L 如式（16）所示。

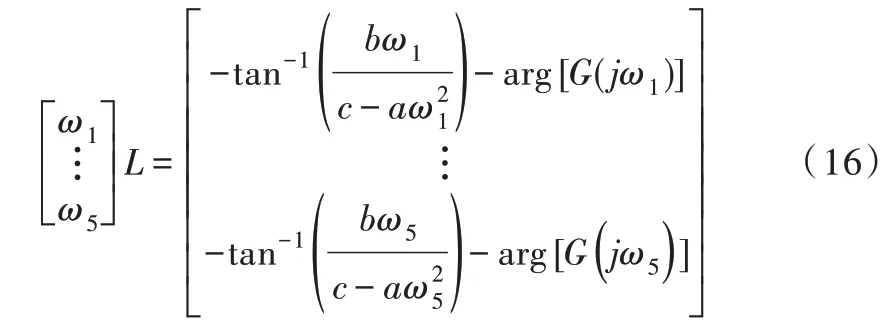
2 蚁群算法

2.1 算法介绍

蚁群算法最早由Dorigo 等［16］于1991 年提出，他们在研究新型算法的过程中，发现蚁群在寻找食物时，通过分泌一种称为信息素的生物激素交流觅食信息从而能快速找到目标，据此提出了基于信息正反馈原理的蚁群算法。

蚁群算法主要应用于求解01 背包问题、最优解问题、TSP 问题等，目前已逐渐应用于其它领域。作为启发式优化算法，其以较佳的全局搜索能力、较快的收敛速度而广泛应用于各类寻优案例中。其优点：①采用正反馈机制，使得搜索过程不断收敛，最终逼近最优解；②每个个体可以通过释放信息素来改变周围环境，且每个个体能够感知周围环境的实时变化，个体间通过环境进行间接通讯；③搜索过程采用分布式计算方式，多个个体同时进行并行计算，极大提高了算法计算能力和运行效率；④启发式的概率搜索方式不容易陷入局部最优，易于寻找到全局最优解。

其算法步骤如下：

步骤1：初始化参数，包含蚁群规模N*D，信息素挥发程度因子Rho，信息素常数Q，转移概率常数p0，最大迭代次数iter_max，信息素因子Alpha，启发函数因子Belta。

步骤2：构建解空间，将各蚂蚁随机置于不同位置，对每个蚂蚁，按照转移概率计算公式，确定其下一个位置。

步骤3：更新信息素，计算各蚂蚁所在位置的信息素含量，根据信息素迭代公式对各位置上的信息素浓度进行更新，同时记录当前迭代次数的最优解。

步骤四：判断是否终止，若达到最大迭代次数，则终止计算，输出最优解，否则，返回步骤2。

利用蚁群算法进行优化的参数为重要频率段中的D个频率点，即算法随机生成N*D 维种群，代入到设定的适应度函数中求解出适应度值，再通过不断更新种群位置，迭代求解出适应度全局极值以及对应的最佳D 个频率点。

2.2 适应度函数

适应度函数的好坏直接影响着智能优化算法性能好坏［17］，时间乘以误差绝对值积分是工程中常用的误差积分准则之一，由于其调节时间短，并且系统参数的细微改变可以使得指标有明显变化，能够很好地反映控制系统性能，因此具有良好的选择性和实用性［18］。ITAE 是时间乘以误差绝对值积分的性能指标，本文中的ITAE 值代表着曲线的拟合度，值越小代表拟合程度越高，以ITAE 为参考指标对求得的参数进行分析，ITAE 表达式如式（17）所示。

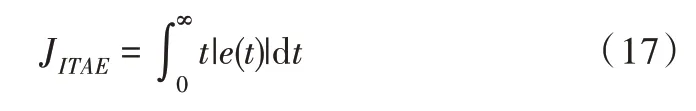
采用累加和形式，在采样时间（0，T）内将积分区间等分成n 个子区间，可近似表示成如式（18）所示。

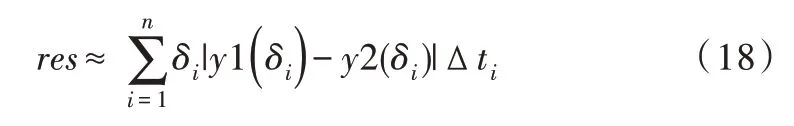
式（18）中，y1 表示原始系统的阶跃响应，y2 表示辨识后模型的阶跃响应，δi为[ti-1,ti](t0=0,tn=T)中的某个数，Δti为一个极小值。

3 仿真实验

为了验证通过本文改进方法得到的辨识参数具有更好的准确性和稳定性，考虑文献［19］给出的串级系统外环高阶时滞对象如式（19）所示。

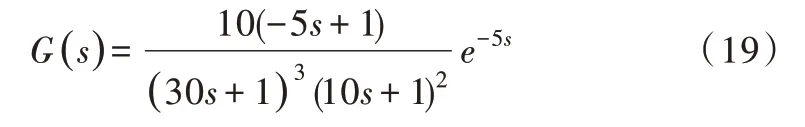
假定输入信号u（t）为阶跃信号，通过上述提到的频率辨识方法，可求出G（s）的穿越频率为0.030 8，即蚁群算法中个体位置范围为［0，0.030 8］。由于蚁群算法受其参数选取的严重影响，文献［20-21］对蚁群算法的参数进行了优化，并对比了多组实验，得出最佳参数组合的取值范围。依据此文献，对各参数进行选值：蚁群规模N 为50，D 为5，Rho 为0.7，Q 为100，p0 为0.2，Alpha 为2，Belta 为5，最大迭代次数为100。依次运行5 次后，每次得到5 个最优频率点，计算出其平均值和方差如表1 所示。

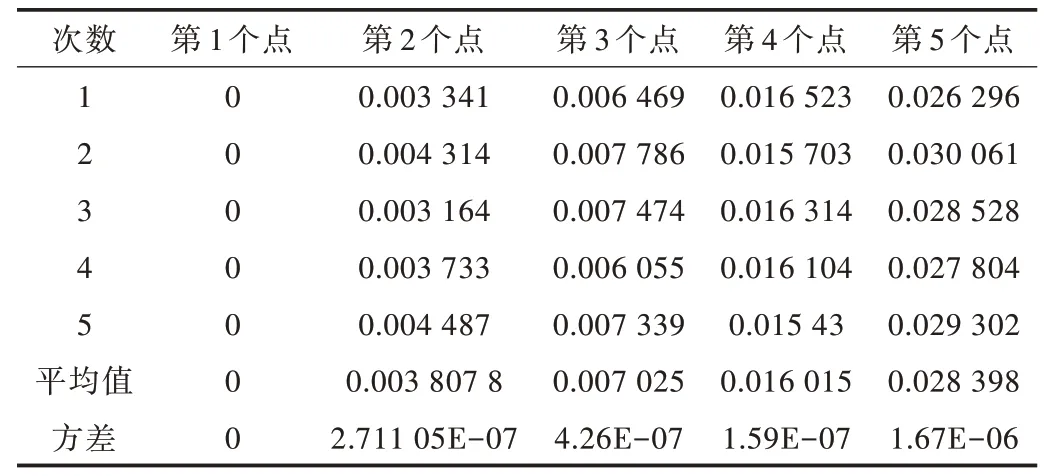
Table 1 Algorithm data表1 算法数据

由表1 方差可得，该算法求出的最优点比较稳定，选取表1 中5 个点的平均值，计算出二阶时滞模型各参数如表2 所示。

Table 2 Model parameter表2 模型参数

对于高阶系统，工业中普遍采用一阶时滞模型进行建模，利用最小二乘法计算模型参数［22］，也常使用基于1/1Pade 逼近的二阶模型拟合法［9］。表3 分别为采用传统一阶模型辨识法、1/1Pade 逼近法、传统二阶加时滞模型法及由本文方法所得出的传递函数模型。求出ITAE 指标，本文的ITAE 值代表曲线拟合度，ITAE 值越小拟合程度越高。

Table 3 Results of four identification methods表3 4 种辨识方法结果

图1 为上述4 种辨识方法所得出的Nyquist 图，其中黑色实线是模型原型，蓝色虚线为传统一阶方法，绿色实线为1/1Pade 逼近法，红色实线为传统二阶加时滞方法，红色虚线是本文方法，图2 为其部分放大图（彩图扫OSID 码可见）。

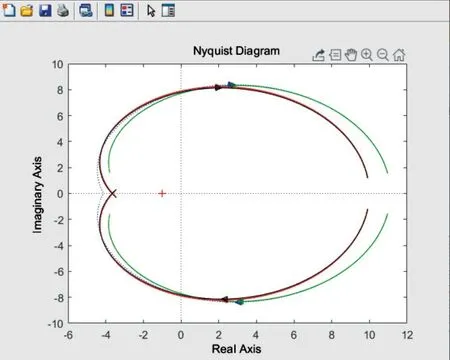
Fig.1 Nyquist diagram图1 Nyquist 图

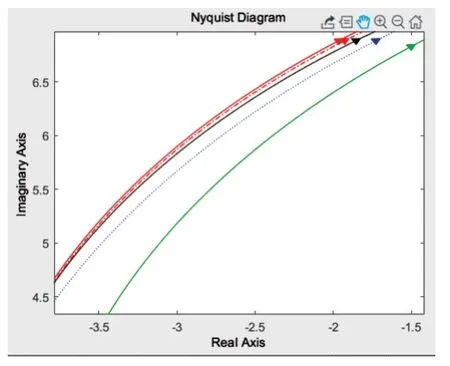
Fig.2 Partial enlarged view of Nyquist图2 部分Nyquist 放大图

同样，考虑文献［19］中给出的串级系统内环高阶对象如式（20）所示。

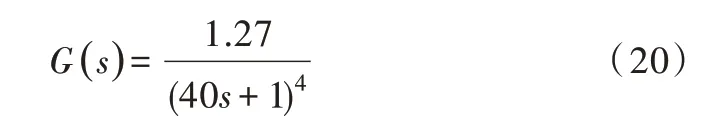
采用上述同样的方法，可求出G（s）的穿越频率为0.025，即蚁群算法中个体位置范围为［0，0.025］。分别为采用传统一阶模型辨识法、1/1Pade 逼近法、传统二阶加时滞模型法及本文方法，所得出的传递函数模型如表4 所示，并在此基础上求出ITAE 性能指标。

Table 4 Results of four identification methods表4 4 种辨识方法结果

图3 为上述4 种辨识方法所得出的Nyquist 图，其中黑色实线是模型原型，蓝色虚线为传统一阶方法，绿色实线为1/1Pade 逼近法，红色实线为传统二阶加时滞方法，红色虚线是本文方法，图4 为其部分放大图（彩图扫OSID 码可见）。

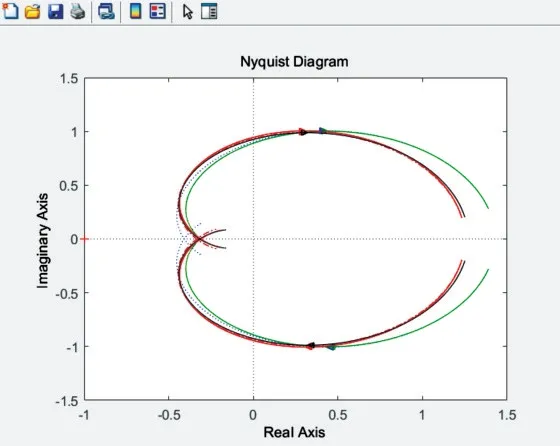
Fig.3 Nyquist diagram图3 Nyquist 图

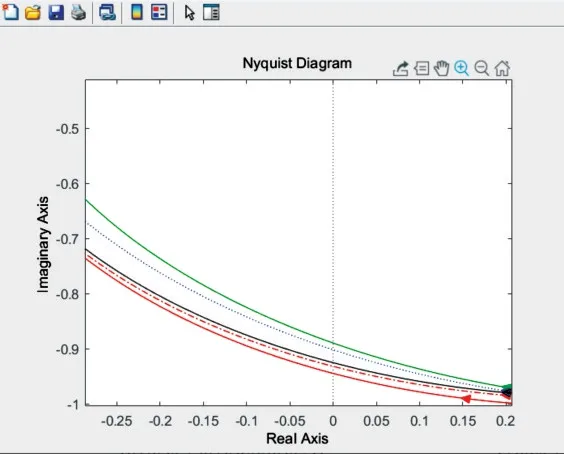
Fig.4 Partial enlarged view of Nyquist图4 部分Nyquist 放大图

由图1—图4 的Nyquist 图及ITAE 指标可知，本文基于二阶加时滞模型的改进方法与传统一阶方法、Pade 逼近法、二阶时滞方法相比，与实际对象模型的拟合精度更高，在某些频率上能够达到完全拟合的效果，并且有效避免了传统二阶时滞方法中特征频率选取点的随机性对最终结果的影响，可以通过使用较少的频率点获得更优的模型参数。

4 结语

本文将蚁群算法运用在高阶时滞系统的辨识中，是对普通二阶时滞模型方法的一种改进，根据系统正常运行时产生的数据，求取对象的重要频率段，再通过蚁群算法，获取较少的特征频率点，最终通过幅频特性确定最终模型，并使得最终模型的参数更接近最优值。Matlab 仿真结果表明，该方法对高阶时滞对象具有更好的辨识效果，与传统的一阶方法和二阶时滞方法相比，具有更高的模型精度，可应用于实际工业生产模型辨识。