从一道考题的多解看初中数学几何解题能力的培养
黄江泉
(广西桂平市南木镇第一初级中学 537226)
在2019年广西贵港市中考的数学试题中,有下面这道题目:
已知:△ABC是等腰直角三角形,∠BAC=90°,将△ABC绕点C顺时针方向旋转得到△A′B′C,记旋转角为α,当90°<α<180°时,作A′D⊥AC,垂足为D,A′D与B′C交于点E.
(1)如图1,当∠CA′D=15°时,作∠A′EC的平分线EF交BC于点F.

图1 图2
①写出旋转角α的度数;
②求证:EA′+EC=EF;
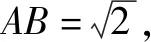
这题属于四边形综合题,考查了旋转变换,全等三角形的判定和性质,相似三角形的判定和性质,三角形的三边关系等知识,综合性强,难度大,方法灵活,有多种不同解法.
(1)②的思路一:在EF上截取EG=EC,先证△CEG为等边三角形,再证△CGF≌△CEA′即可.
(1)②的思路二:过C作CG∥A′D交EF于G,先证△CEG为等边三角形,再证△CGF≌△CEA′即可.
(1)②的思路三:延长ED到G,使DG=DE,先证△CEG为等边三角形,再证△CGA′≌△CEF即可.
(2)的思路一:连结A′F,由△CGF≌△CEA′可知CA′=CF,从而可证△A′CF为等边三角形,进而可证A′E同时平分∠FEB′和∠FA′B′,从而△A′EF≌△A′EB′,于是得B′与F关于A′D对称,只要求出AB′即可.
(2)的思路二:过A′作A′M⊥B′E,得△A′ME和△A′MB′分别为含有45度和30度角的特殊直角三角形,通过计算证明B′E=EF,进而可得到B′与F关于A′D对称,只要求出AB′即可.
(1)②的思路一、思路二用到了数学中最常用的截长法,其中思路二用到了“角平分线+平行线”得到的隐含等腰三角形,(1)②的思路三用到了数学中最常用的补短法,(2)的思路一用到了角平分线、全等三角形等基本图形(模型),(2)的思路二用到了特殊直角三角形的基本图形(模型),并且所有的思路中都用到了角平分线、等腰三角形、等边三角形、直角三角形、等腰直角三角形、全等三角形等基本图形的判定和性质.通过对本题多种解法的分析不难发现,培养和提高初中生的几何解题能力要从以下几方面入手:
一、熟悉几何基本图形和基本结论是培养几何解题能力的前提
几何基本图形和基本结论是几何知识的重要组成部分,是所有几何解题的前提,角平分线、中线、高、点到直线的距离、动点到两定点距离之和的最小值、等腰三角形、等边三角形、直角三角形、等腰直角三角形、平行四边形、矩形、菱形、正方形、垂径定理、过圆外一点作圆的切线、全等三角形、相似三角形等基本图形及其结论,既是考试考查的重点,也是所有解题的基本依据,我们要熟练掌握.如:
例1(广西贵港2016-12)如图3,ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②S=AC·BC;③④S△OCF=2S△OEF成立的个数有( ).
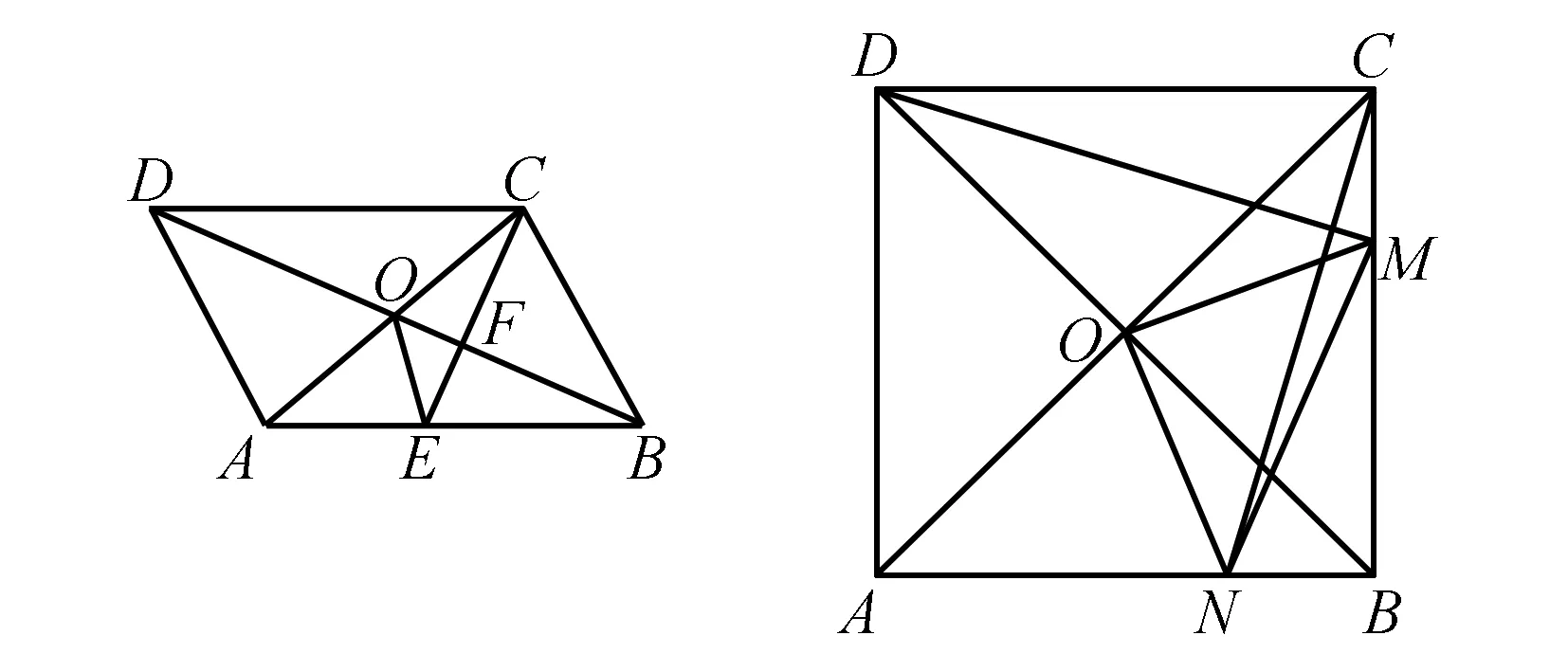
图3 图4
A.1个 B.2个 C.3个 D.4个

A.2 B.3 C.4 D.5
这些题目表面看起来很复杂,但实质都是考查几何基本图形及其结论.例1考的是角平分线、平行四边形、等边三角形等图形的性质,例2考查的是相似三角形的判定和性质、全等三角形的判定与性质以及正方形的性质.只要掌握相似三角形和全等三角形的基本图形,问题不难解决
二、理解定义、定理、公理、判定、性质是培养几何解题能力的基础
理解定义、定理、公理、判定、性质,就是不仅要熟记定义、定理、公理、判定、性质的结论,还要熟记定义、定理、公理、判定、性质的条件、适用范围、注意事项等,它是几何解题的基础.如:


图5
本题中,不少考生因没有在意弧长公式中圆心角的意义,结果将120度直接代入计算,答案当然错了.
三、善于发现图中的隐含图形是培养几何解题能力的关键
隐含图形是指等腰三角形、等边三角形、平行四边形等特殊的图形在整个图形中表现出来的一部分,如“角平分线+平行线”隐含有等腰三角形,“中点+垂直”也隐含有等腰三角形,“角平分线+等腰”隐含有垂直平分,三角形含有30度和45度角则隐含可构造特殊直角三角形等等.解题中如果我们能够充分发现这些隐含图形,会非常有利于问题的分析和解决.如:
例4(广西贵港2019-24)如图6,在矩形ABCD中,以BC边为直径作半圆O,OE⊥OA交CD边于点E,对角线AC与半圆O的另一个交点为P,连接AE.

图6
(1)求证:AE是半圆O的切线;
(2)若PA=2,PC=4,求AE的长.
本题中,条件出现了“中点+垂直”,隐含有等腰三角形,因而可以通过“延长AO、DC相交于M,或延长EO、AB相交于N”这样的辅助线,帮助解决问题.
例5(广西贵港2017-26)已知,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处.
(1)如图7,若点D是AC中点,连接PC.
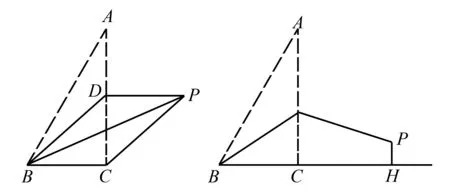
图7 图8
①写出BP,BD的长;
②求证:四边形BCPD是平行四边形.
(2)如图8,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长.
本题(2)的关键是 “角平分型全等三角形隐含着BD是等腰三角形的高”,从而想到连结AP并延长BD交AP于E,然后过P作PF⊥AC于F即可构造“双垂直型相似”,利用相似列比例式即可把问题解决.
例6(1)(广西贵港2015-10)如图9,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( ).

图9 图10
A. 0 B. 1 C. 2 D. 3
(2)(广西贵港2017-11)如图10,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( ).
A.4 B.3 C.2 D.1
上述两题均隐含有两边为定长的三角形这样的隐含图形,因而问题实际上是“已知两边求第三边的范围”,这样利用三角形的三边关系即可解决.
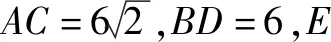
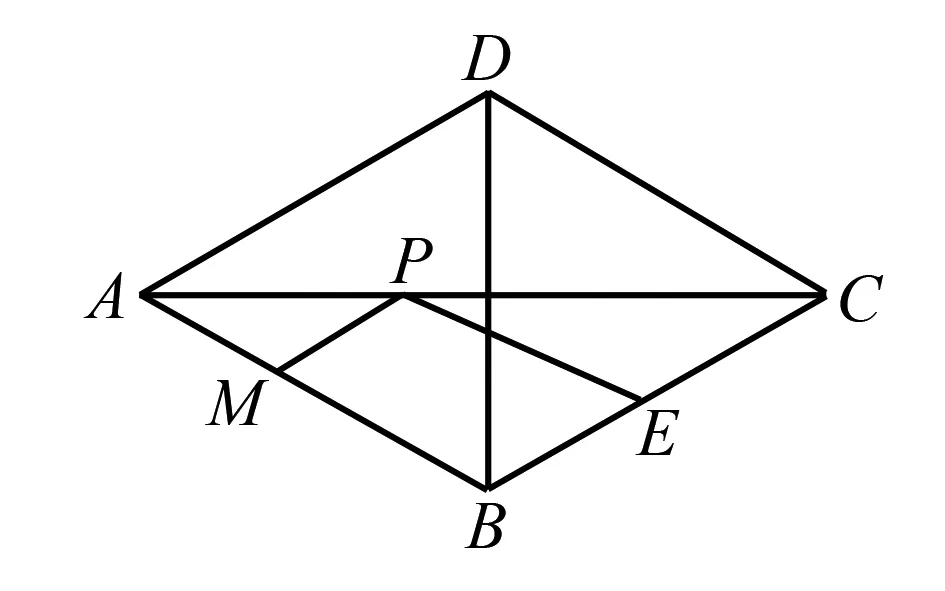
图11

本题中隐含两个最常用模型(图形)——将军饮马模型和点到直线模型,因此,作E关于AC的对称点F,过F作FM⊥AB,则FM即为所求.
四、掌握基本的几何变换是培养几何解题能力的桥梁
几何变换是平面几何的重要内容之一,是研究几何关系的基本方法.平移、旋转、轴对称是初中几何的基本变换,熟练掌握这些变换是培养和提高几何解题能力的桥梁.
例8(广西贵港2018-26)如图12,已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线l相交于点P.

图12 图13
(1)当P与O重合时(如图13所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;
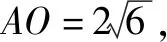
请直接写出AB和PB的长.
本题(2)的关键是进行平移变换,过B作BC⊥AO于C,即得△ABC∽△PBM,由对应边成比例即可;(3)的关键仍然是利用“双垂直型相似”列比例式解决,只是要注意不同位置的存在,要分类讨论.
例9(广西贵港2016-26)如图14,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.

图14 图15 图16
(1)如图15,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图16,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
本题(2)的关键是进行旋转变换构造全等三角形,将△ABM绕点A逆时针旋转90°得△ADM′,即可证明△ADM′≌△AMN,M′N=MN,M′D=BM,且△M′DN为直角三角形,故问题顺利解决.
五、掌握数学基本方法是培养几何解题能力的突破口
数学基本方法论是数学解题的突破口,几何解题更是离不开数学基本方法.几何变换法、面积法、割补法、截长法、补短法等都是几何解题中最常用的数学方法.如:


图17 图18
(2)(广西贵港2018-17)如图18,在Rt△ABC中,∠ACB=90°,AB=4,BC=2,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,则图中阴影部分的面积为____(结果保留π).

图19

这些与面积有关的问题,都要用到割补法等数学基本方法.其中(1)还要注意到图中的隐含图形——等边△AOD,才能求出有关的圆心角;(2)要分割成两个扇形和两个三角形面积的和与差;(3)用到的是非常典型的平行轴分割的方法以及二次函数最大值的模型.
例11(广西贵港2019-12)如图20,E是正方形ABCD的边AB的中点,点H与B关于CE对称,EH的延长线与AD交于点F,与CD的延长线交于点N,点P在AD的延长线上,作正方形DPMN,连接CP,记正方形ABCD,DPMN的面积分别为S1,S2,则下列结论错误的是( ).

图20
A.S1+S2=CP2
B.AF=2FD
C.CD=4PD
本例可用反证法的思想,答案A明显正确,假设B正确,很容易推导出C也正确,即B与C同对同错,所以只能选D.
六、掌握几何证明的常见分析方法是培养几何解题能力的重点
几何证明的常见分析方法很多,如综合法、分析法、反证法、枚举法(穷举法)、完全归纳法、不完全归纳法……等等,但最常用的方法有综合法、分析法和分析综合法.熟练掌握这些常见的分析方法是我们探求解题途径的重点和关键.
分析法是从求证的结论入手,以公理、定理为根据,寻求所必须的条件,再从所需条件出发,一步一步地寻求到所需的条件为已知条件时,命题即得证,这种方法也叫“执果索因”法;而综合法是从已知条件为出发点,以公理、定理为依据,一步步推导出欲证的结论,这种方法也叫“由因导果”法;分析综合法将分析法和综合法结合起来,即先从结论入手看需要什么条件,再从已知出发看可导出什么结论,如果这两者正好一致,问题即可解决,这种方法也叫“两头凑”的方法,通常情况下我们都用这样的分析方法.如前面例4的(1):
从结论(求证)入手,要证AE是半圆O的切线,就要过O作OF⊥AE于F,证OF=OB,于是要证△AOF≌△AOB,这就要证∠BAO=∠OAF(E),进而要证△ABO∽△AOE或△ABO∽△AFO.

这个分析问题的方法就是分析综合法.
在培养学生几何解题能力的过程中,除了加强学生对几何基本图形和基本结论的熟悉程度,对几何定义、定理、公理、判定、性质的理解,引导学生善于发现图中的隐含图形,掌握好数学基本方法和基本的几何变换以及常见的分析方法外,还要学会对几何结论进行分类,掌握几何难题突破的一般程序等.如对几何结论,我们可以从线段平行、垂直、相等、不等以及角相等、不等等方面进行分类;而对几何难题的突破,可从完善图形(重新画图)、标识等量、发现隐含图形、挖掘图形关系(全等或相似)等方面入手.
下面通过一个具体例子来体会一下:
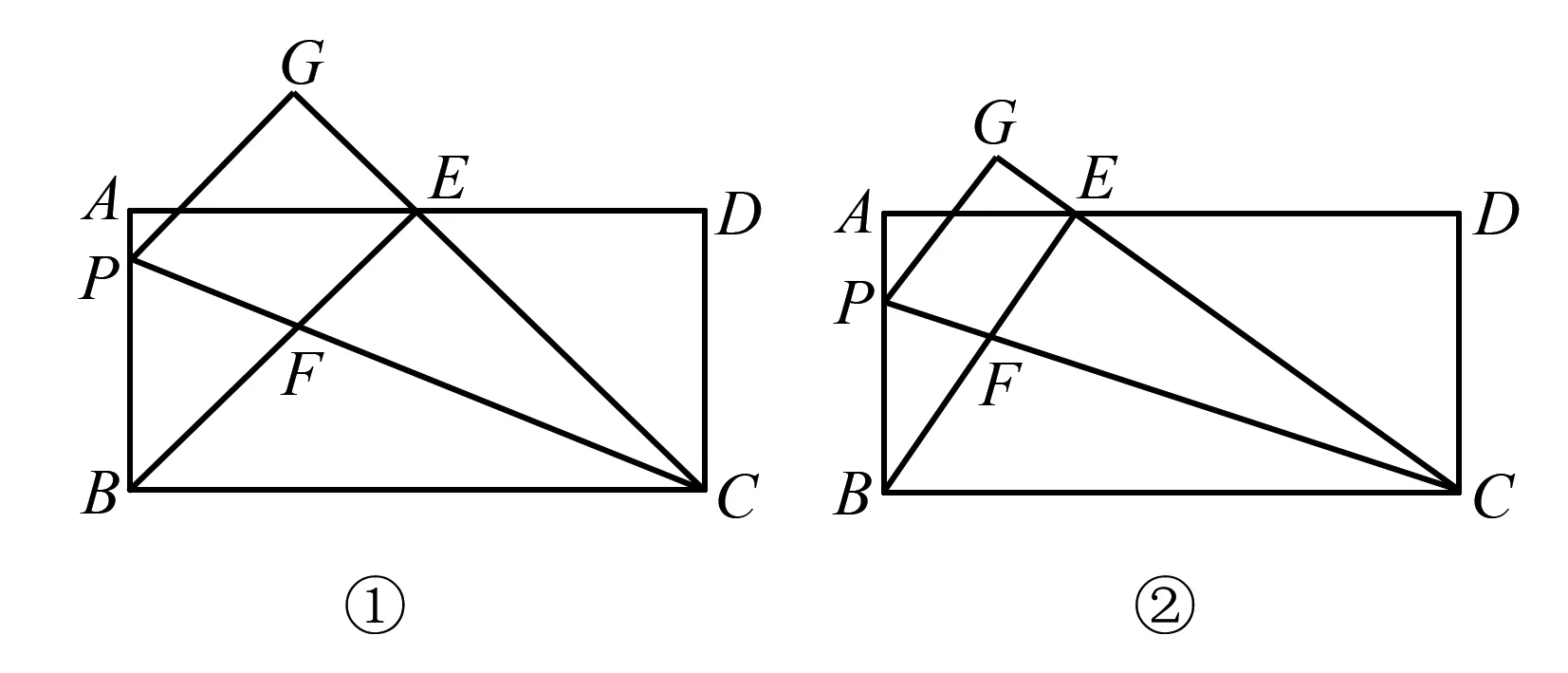
例12(包头2018-25)如图21,在矩形ABCD中,AB=3,BC=5,E是AD上的一个动点.
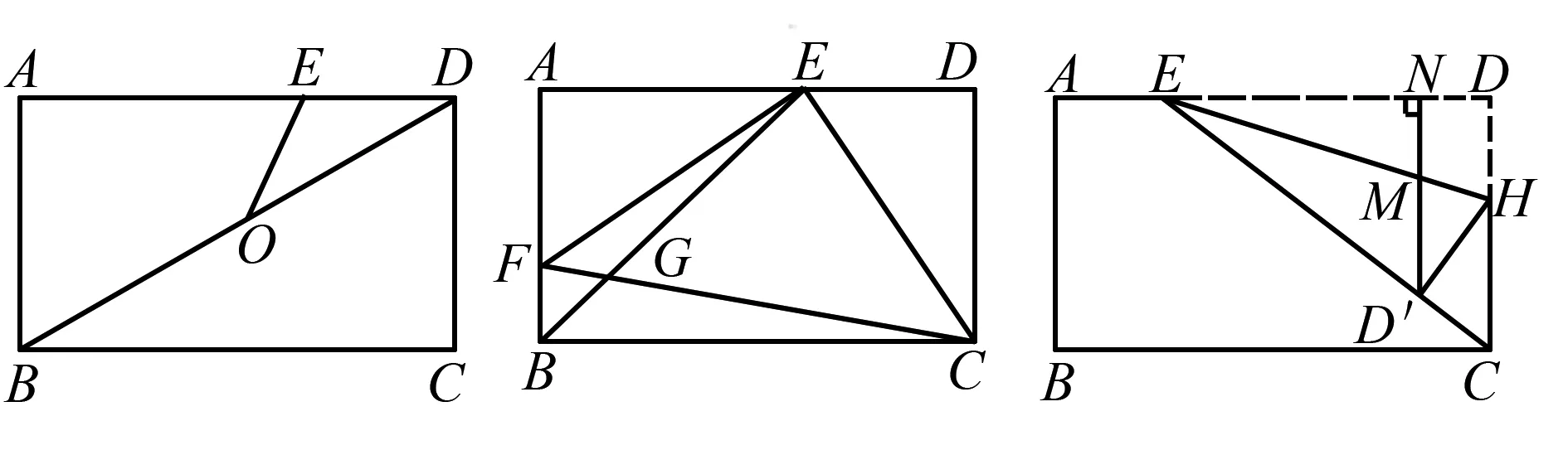
图21 图22 图23
(1)如图21,连接BD,O是对角线BD的中点,连接OE.当OE=DE时,求AE的长;
(2)如图22,连接BE,EC,过点E作EF⊥EC交AB于点F,连接CF,与BE交于点G.当BE平分∠ABC时,求BG的长;
(3)如图23,连接EC,点H在CD上,将矩形ABCD沿直线EH折叠,折叠后点D落在EC上的点D'处,过点D′作D′N⊥AD于点N,与EH交于点M,且AE=1.
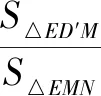
②连接BE,△D′MH与△CBE是否相似?请说明理由.
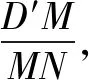
再看一例:
例13(宜昌2018-23)在矩形ABCD中,AB=12,P是边AB上一点,把ΔPBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.(1)如图24①,若点E是AD的中点,求证:△AEB≌△DEC;(2)如图24②,①求证:BP=BF;②当AD=25,且AE 图24 问题(1)的思路比较具体、简单,是一对“一线三垂直型”全等;(2)中的①只要注意到翻折隐含着角平分线,由“角平分线+平行线”即可;(2)中的 ②相当于要求PC,从何入手?只要注意到图中含有“一线三垂直”型相似三角形,即可求得EC=20,BE=15,再注意到PG=BP=BF,用“平行”型相似(△CEF∽△CGP)即可求得BP,进而求得PC;(2)中的③则要注意到PG与BF平行且相等,连结FG即可得BPGF为平行四边形,故GF=BP且∠EFG=∠FBP,所以△GEF∽△EAB,由相似成比例即可解决. 当然,我们强调对数学图形、数学结论、数学方法和几何变换的掌握,不是简单的把它们背下来就可以了,而是要在实际应用中去理解、去体会,学会举一反三、触类旁通,才能不断形成和提高解题的能力.