一次函数背景下的存在性问题
王帅兵
(湖南省郑州市孜文教育信息咨询有限公司 450000)
一、两定一动型,注意好“一上一下”
两定一动型,是指在给定两个点的情况下,另一点在一条线上运动所产生的面积问题,解决这类问题,要做好题目分析,有一边与坐标轴平行时直接求解;没有边与坐标轴平行时,用好“铅锤法”(或“割补法”),同时注意好“一上一下”.
例1如图1所示,一次函数y=2x+4的图像与坐标轴分别交于点A、B,在一次函数的图象上是否存在一点P,使得△AOP的面积为3?
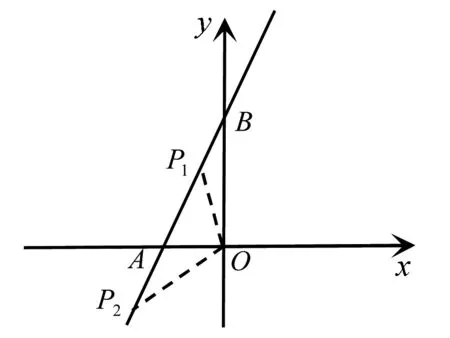
图1
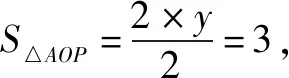
例2如图2所示,直线y=1/2x与直线y=-x+3相交于点A,点B是直线y=1/2x上的一个点,且横坐标为4.如果点P是直线y=-x+3上的一个动点,且满足△ABP的面积为9,那么点P的坐标为____.

图2 图3 图4

二、等腰三角形,用好“两圆一线”
在一次函数的背景下,等腰三角形的存在性问题可以借助图形的基本性质来解,利用同端点、等长度作圆和线段垂直平分线.
例3如图5所示,直线y=x+4与坐标轴交于点A和点B,在x轴上是否存在点P,使得△ABP为等腰三角形?若存在,求出所有满足条件的点P的坐标.
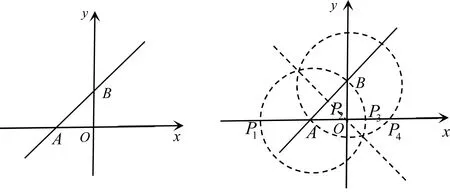
图5 图6

三、直角三角形,利用顶点来分类
对于直角三角形的存在性,可以利用顶点来分类,然后结合具体条件求解.
例4如图7所示,在平面直角坐标系xoy中, 三角板的直角顶点P的坐标为(2,2), 一条直角边与x轴的正半轴交于点A,另一直角边与y轴交于点B, 三角板绕点P在坐标平面内转动的过程中,当△POA为直角三角形时,请求出所有满足条件的点B的坐标.
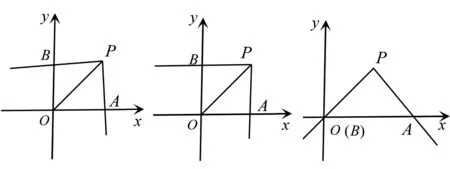
图7 图8 图9
思路分析分析题设条件可得,∠POA=45°,不可能为直角,△POA的另两个角可以是直角.如图8,当OA⊥AP时,可求出点B的坐标为(0,2);如图9,当OP⊥PA时,点B和点O重合,点B坐标为(0,0).综上所述,点B的坐标为(0,2)或(0,0).
四、等腰直角三角形,借助弦图轻松解
等腰直角三角形的分类问题,可以在构造基本直角的情况下,借助弦图求解.
例5如图10所示,直线y=-2x+4与坐标轴交于点A和点B,在第一象限内是否存在点P,使得△ABP为等腰直角三角形?
图10 图11
思路分析由题设条件易得,A(2,0)、B(0,4),OA=2,OB=4.利用Rt△AOB作弦图,如图11所示,其中P1、P2、P3是满足条件的点.利用弦图中的全等三角形的性质,以及线段长与坐标的相互转化,可得三点的坐标分别为:P1(4,6)、P2(6,2)、P3(3,3).
五、全等三角形,对应后综合求解
全等三角形的存在性问题,要注意好顶点的对应,然后借助多种基本方法解题.
例6如图12所示,在平面直角坐标系中作矩形OABC,点B坐标为(4,8),将△ABC对折,使点A与点C重合,折痕交AB于点D,坐标系内是否存在点P(除点B外),使△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.

图12 图13 图14
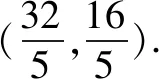
六、等距离轨迹问题,借助坐标轴三角形构造相似
在一次函数背景下的等距离轨迹问题,可以借助一次函数图像与坐标轴的交点,构造相似图形,求出点的坐标,进而找到点所在直线的表达式.


图15 图16
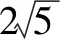
综上,解决一次函数的存在性问题,一定要研究好背景图形,调用基本技巧和方法,构图确定位置,画图解答.
——《李叔同——弘一大师行踪图典》评介
——《认识直角》教学片断与解读

