关于线性算子的弱统计收敛

鲍玲鑫

(福建农林大学计算机与信息学院，福建福州350002)

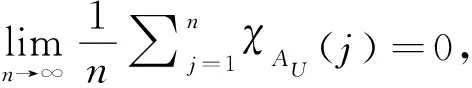
经典统计收敛的概念是在X=R中引入的，此后基于不同的目的，出现各种各样推广形式的统计收敛.概括地讲统计收敛沿着以下两个方向推广：一是在更为一般的空间中定义统计收敛，例如，局部凸空间[3]，包括赋予弱拓扑的Banach空间[4-6]和一般拓扑空间[7].另一个是利用不同的极限过程来定义统计收敛，例如，A-统计收敛[8]、lacunary统计收敛[9]以及最为一般的理想(或滤子)收敛[10-11].

伴随着每一种推广形式的统计收敛的引入，关于统计收敛与经典收敛之间的关系都是人们研究的热点问题.其中一个核心的定理是度量空间X中序列的统计收敛与几乎处处收敛是等价的，即序列(xn)⊂X统计收敛于x∈X当且仅当存在一个统计零集G⊂N使得(xn)n∈N G在度量拓扑意义下收敛于x(例如X=R,可参考文献[12-13]).Maio等[7]证明了当X是第一可数空间时，则上述定理也是成立的.尽管如此，但该结论反过来却不成立.具体地，第2节中的第1个反例即构造了一个非第一可数的拓扑空间(X,τ)使得定义在X上统计收敛与几乎处处收敛是等价的.

Bao等[14]证明了对于任意一个自由的滤子F⊂2N，都存在一族统计测度S使得S-收敛等价于F-收敛，反之亦然.最近，Cheng等[15]证明了一系列由单一统计测度定义的滤子收敛的特征，并在文末提出如下问题(参见文献[15]，Remark 5.7).

问题1由单一统计测度μ定义的统计收敛是否等价于μ-几乎处处收敛？或特别地，由单一退化的统计测度μ定义的统计收敛(或等价地，超滤子U-收敛)是否等价于μ(U)-几乎处处收敛？

第1节中第2个反例构造了Banach空间X中的一个序列(xn)以及一个超滤子U，使得(xn)是U-收敛的但不是U-几乎处处收敛的.从而问题1的答案是否定的.

1 两个反例

如果N的一个子集族I满足：(i) 若A,B∈I，有A∪B∈I;(ii) 若A∈I，有2A∈I，则称I为N上的一个理想.如果N∉I(相应地，I≠∅)，则称理想I称为真的(相应地，非平凡的).设F为N的一个子集族，如果IF≡{NF:F∈F}是一个理想，则F称为一个滤子.

定义1设F ⊂2N是一个非平凡的滤子(等价地，IF是一个非平凡的理想).

(i) 拓扑空间X中的序列(xn)称为F-收敛于x∈X是指对任意x的邻域U,BU∈F,或等价地,AU∈IF.其中AU={n∈N:xn∉U}及BU={n∈N:xn∈U}.(xn)F-收敛于x当且仅当(xn)IF-收敛于x.

(ii) 特别地，Banach空间X中的序列(xn)称为F-收敛于x∈X是指对任意的ε>0,B(ε)∈F,或等价地，A(ε)∈IF.其中A(ε)={n∈N:‖xn-x‖≥ε}及B(ε)={n∈N:‖xn-x‖<ε}.

(iii) 拓扑空间X中的序列(xn)称为F(或IF)-几乎处处收敛于x∈X是指存在G∈IF使得(xn)n∈G按通常拓扑意义下收敛于x.

设F是N上的一个滤子.如果∩{F∈F}=∅，称滤子F为自由的.在N上所有滤子构成的集F′上定义如下自然序“≻”：F1≻F2如果F1⊃F2.F′中按照自然序意义下的极大元称为N上的超滤子.从而由Zorn引理以及滤子的定义可知任意一个滤子F，都存在N上的一个超滤子U使得U≻F.滤子F是一个超滤子当且仅当对任意的A⊂N，有A∈F或NA∈F.若F是一个自由的超滤子， 则F不包含任意有限子集，或等价地，包含Fréchet滤子FF≡{A∈N:(NA)#<∞}.

拓扑空间X中序列的统计收敛是否等价于几乎处处收敛很大程度上由空间的拓扑结构决定的. 正如引言中所述的，有大量的文献在第一可数的拓扑空间(包括实空间、度量空间等)框架下证明了统计收敛与几乎处处收敛是等价的.但该结论反过来是否成立仍然是一个未解决的问题.本文给出如下反例：

例1存在一个非第一可数的拓扑空间(X，τ),X中序列的统计收敛与几乎处处收敛是等价的.

证明令Ist={A⊂N:δ(A)=0}，则Ist-收敛即为通常意义下的统计收敛.记Fst={A⊂N:NA∈Ist}.令U表示任意一个包含滤子Fst的超滤子，则不难验证U是一个自由的超滤子.

第1步.定义一个非第一可数的拓扑空间(X,τ).

第2步.证明(X,τ)中序列统计收敛与几乎处处收敛是等价的.

因为Ist-几乎处处收敛总是意味着Ist-收敛，只需证明Ist-收敛意味着Ist-几乎处处收敛.设(xn)⊂X，Ist-收敛于x∈X.下面要证明存在G∈Fst使得(xn)n∈G在拓扑τ意义下收敛于x.分为如下两种情形：

(i) 若x≠0，即存在某个k∈N使得x=k.注意到单点集{k}是其自身的一个领域，只需令G={n∈N:xn∈{k}}={n∈N:xn=k}∈Fst即完成证明.

(ii) 若x=0,则根据(xn)Ist-收敛于0以及超滤子的相关性质，有如下不难验证的事实：

事实1 令Ak={n∈N:xn=k}，k=1,2,…，则有Ak∈Ist对所有的k∈N.

事实2 对任意的B∈U，根据τ的定义可知，∪k∈N BAk∈Ist.

事实3 对任意的B⊂N，则有B∈U或NB∈U.则根据事实2可知，∪k∈BAk∈Ist或∪k∈N BAk∈Ist.

断言：存在B1与B2使得N=B1∪B2,∪k∈B1Ak∉Ist及∪k∈B2Ak∉Ist.

由N=B1∪B2以及超滤子的性质可知，B1∈U或B2∈U.不失一般性，假设B1∈U，则{n∈N:xn∉U(0,B1)}=∪k∈B2Ak.又因为(xn)Ist-收敛于0,有∪k∈B2Ak∈Ist.这与上面断言是矛盾的.

下面只需证明断言.任取一个足够大的n1∈N使得

注意到Ai∩Aj=∅对任意的i≠j.则至多有限多个“Ak”与{1,2,…,n1}有非空的交集.从而存在m1∈N使得

其中M1≡{1,2，…,m1}⊆N.根据事实1,可以选取足够大的n2∈N使得

且

重复上面的方法不断进行下去，可以得到两个单调递增的自然数序列{nj}与{mj}使得

且

这证明了

i.e.，B1∉Ist.同理可以证明B2∉Ist.从而断言得证.

例2设X是一个Banach空间.存在X中的一个序列(xn)以及N上的一个自由的超滤子U使得(xn)是U-收敛于0的但不是U-几乎处处收敛于0的.

证明第1步.定义目标序列(xn).

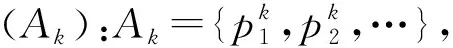
第2步.构造目标超滤子U.令={NAk:k∈N},ε≡{A∈N:AkA是有限集对所有的k∈N}及=∪ε.则显然包含了Fréchet滤子F.下面证明可生成一个滤子，即证明任意有限个中的元素都有非空的交.事实上，对任意的A,B∈ε,Ak(A∩B)=(AkA)∪(AkB)是一个有限集对所有的k∈N.从而A∩B∈ε.进一步地，对任意的A∈ε与k∈N,不难看出A∩(NAk)是一个非空集(实际上，是一个无限集).此外，由(Ak)的定义可知，(NAk)∩(NAj)≠∅对所有的k,j∈N.记表示由生成的滤子，则是自由的.任取一个包含的超滤子U,则U也是自由的.

第3步.验证(xn)是U-收敛于0但非U-几乎处处收敛于0 .

2 线性算子的弱统计收敛

考虑引入有界线性算子序列在弱算子拓扑意义下的统计收敛.为此，先回顾一下Banach空间中序列在弱拓扑意义下的统计收敛：Banach空间X中的序列(xn)称为弱统计收敛于x∈X是指对任意的ε>0以及任意的x*∈X*，A(x*;ε)={n∈N:|〈x*,xn-x〉|≥ε}具有自然密度0.如果(xn)弱统计收敛于0,称(xn)为弱统计零序列.

1) (Tn)称为弱统计收敛于T是指对任意的x∈X以及任意的x*∈X*,δ({n∈N:|〈x*,Tnx-Tx〉|≥ε})=0对任意的ε>0.此时，记为T=w-st-limTn.

2) (Tn)称为几乎处处弱收敛于T是指存在一个统计零集G∪N使得(Tn)n∈N G在弱算子拓扑意义下收敛于T.此时，记为T=al-w-limTn.

引理1(可参阅文献[4，16]) 设A1,A2,…是N的一个子集列满足δ(Ai)=1对所有的i∈N.则存在A⊂N使得δ(A)=1且(AAi)#<∞对所有的i∈N.

定理1[4]设X是一个可分的Banach空间.则X*是可分的当且仅当任意有界的弱统计零序列都是几乎处处弱收敛的.

引理2[17]设X是一个可分的Banach空间.则存在一个从l1到X满的有界线性算子.

下面将证明一个Connor-Ganichev-Kadets型定理.

|〈x*,Tnx〉|≤‖x*‖‖Tn‖‖x-xk‖+

|〈x*,Tnxk〉| <ε.

这证明了(Tn)是几乎处处弱收敛于0的.设(Tn)几乎处处弱收敛于0,由定义即可推出(Tn)弱统计收敛于0.从而必要性得证.

充分性.令

S={(xn)⊂X:(xn)有界的弱统计收敛于0}.

则断言S#=X#=c,其中S#表示集合S的基数，c表示连续统的基数.事实上，根据引理2,X#≤c.由于F×X=X,X#≥c,其中F表示定义Banach空间X的数域.从而有X#=c.另外,S#≤cN0=(2N0)N0=2N0·N0=2N0=c.注意到F×S=S,S#≥c.这意味着S#=c=X#.定义双射g:X→S.

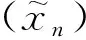
则(Tn)一列有界的连续线性算子.对任意x∈X，x可以表示为x=λx0+y.则(Tn(x))=λ(xn)弱统计收敛于0.这说明(Tn)弱统计收敛于0.但当λ≠0,(Tn(x))=λ(xn)非几乎处处弱收敛于0.从而(Tn)非几乎处处弱收敛于0.这与充分性的假设矛盾.