限制择校促进义务教育均衡发展了吗*

● 俞艳霞，王 铮

(东南大学 经济管理学院，江苏 南京 211189)

一、引言

义务教育均衡发展是当前教育研究和教育政策的关键词，其实质是“追求教育平等，实现教育公平”。为促进义务教育均衡化，2014年1月28日，教育部出台《教育部办公厅关于进一步做好重点大城市义务教育免试就近入学工作的通知》(以下简称“通知”)，将北京、上海、南京等19个城市列为重点实施免试就近入学、限制择校政策的城市，意在取缔“择校费”、“特长生”等不正当的择校方式。

限制择校政策是否起到了促进义务教育均衡发展的作用？这一问题的答案取决于限制择校政策的作用机制，主要包括以下两方面：一方面，毋庸置疑，该政策能够有效阻断“择校费”、“特长生”择校渠道，一定程度上促进受教育机会的平等。另一方面，该政策并没有制止择校行为，而只是促使择校方式由不正当的“付费择校”转变为“以房择校”。家庭利用“划片入学”，通过购买优质小学学区房，获取优质义务教育资源，导致学区房价格被巨大的教育需求所引导，重点、普通小学学区房价格出现分化。“以房择校”行为的存在必然使得高收入家庭获得更优质的教育资源，从而不利于促进教育公平。

本文重点检验上述第二个机制，即限制择校政策通过影响学区房房价，不利于低收入家庭获取优质教育资源，从而损害了教育公平，不利于实现义务教育均衡发展。具体方法是借助“通知”出台这一“准自然实验”，采用双重差分法(DID)，通过评估限制择校政策对于学区房房价的影响，分析其对于义务教育均衡发展是否起到促进作用。需要说明的是，本文研究的问题是一项教育政策的效果评估，但同时也属于教育资本化范畴。基于此，在实证部分，首先借鉴已有研究，运用传统特征价格模型估计学校质量对学区房房价的影响；其次，构建并估计双重差分模型，评估“通知”中包含的“限制择校”政策对于学区房房价的影响。从学校质量和限制择校政策两个方面解释重点小学学区房高房价现象，评估政策效果的同时，也为学区房溢价研究提供了一个新的视角。

二、文献综述

国内外对于学区房溢价问题的研究主要采用特征价格模型。Oates(1969)[1]认为特定社区的住宅价格取决于房屋的物理特征、地理位置、房产税税率、公共服务水平、交通通达性等因素，由此构建模型并对住宅价格的影响因素进行了实证研究。Rosen(1977)[2]利用特征价格模型对房价与学校质量进行实证分析，研究发现，两者存在统计意义上的显著正相关关系。Dhar 等(2012)[3]利用康涅狄格州学区边界附近住房交易的重复截面数据，发现考试成绩对住房价格有显著影响。国内对于学区房溢价的经验研究起步较晚。Zheng 等(2008)[4]利用北京市新建住房价格数据估计特征价格模型，发现便捷的交通、高质量学校、环境宜居性等可获得的公共产品和服务的价值都资本化到住房价格中。周京奎和吴晓燕(2009)[5]分析各省教育投资的房地产市场溢价效应，发现中学数量对于房地产市场存在显著且稳定的溢价效应。冯皓和陆铭(2010)[6]基于上海市 52个区域的二手房月度均价，研究“实验性示范性高中”命名对于学区房房价的影响，实证结果表明这一命名作为政府向市场传递优质学校信息的过程，对于房价的影响确实存在。哈巍等(2015)[7]利用搜房网平台的二手房交易数据，估计特征价格模型后得出在控制其他影响房价变量的情况下，相对于二手非学区房，市重点小学的学区房房价高出18.4%，区重点小学高出5.4%。

住房的标准特征价格模型将住房市场价格表示为可观测住房属性的潜在市场价格的线性组合。但现实中，本地公共服务和宜居性等一系列房价影响因素并不是都能被观察到。因此，传统特征价格模型会导致遗漏变量偏误，导致公共品资本化效应难以得到有效估计。遗漏变量问题的对策之一是将紧邻的、属于不同学区的房屋数据进行配对，采用边界固定效应模型或差分法，以消除特定区域的不可观测因素的影响。

Black(1999)[8]开创了边界固定效应法。她利用马萨诸塞州各学区边界附近的房价数据，通过在特征价格模型中添加边界固定效应来控制邻里差别。在此基础上，Fack和Grenet(2010)[9]创造性地采用了房屋配对回归的方法，来控制不可观测的区位特征变量对房价的影响。Gibbons等(2013)[10]匹配临近住房的交易数据，并运用差分模型来解决空间趋势和边界效应等问题。国内一些学者研究学区房溢价时也较多地借鉴了边界固定效应法、配对回归法。胡婉旸等(2014)[11]通过配对差分法估计得出北京重点小学学区房的溢价约为8.1%。张雅淋和赵强(2017)[12]采用配对差分法，将南京市主城区具有代表性的33所小学周边小区进行配对，并进行一阶差分检验，实证结果表明重点小学会给其周边二手房带来14.12%的溢价，省实验和非省实验小学的学区房溢价分别为18.69%和10.81%。张骥(2017)[13]也采用了基于特征价格模型的配对差分法，估计得出相对于非重点小学，北京市重点小学的学区房溢价达到24.3%。此外，张牧扬等(2016)[14]将租金收益回报率作为因变量，研究上海市学区房溢价，租金收益率以比值的方式，一定程度上消除了遗漏变量偏误。

双重差分法是国内政策效果评估领域应用最广的研究工具，但在住房价格、教育资本化研究中的应用并不是很广泛，主要有以下几个方向。一是对于住房价格的研究。张德荣和郑晓婷(2013)[15]用双重差分模型对于住房“限购”政策的效果进行评估，得出我国70个实行“限购”的大中城市中，限购政策降低了新房和二手房的价格上涨率，但该结果不具有统计意义上的显著性。王玉玺等(2017)[16]利用“国八条”出台这一“准自然实验”，采用双重差分法分析限购政策对房价的影响，发现主要城市的限购政策并未对全国新建商品房的均价起到抑制作用。二是对于学区房溢价的研究。Bogart和Cromwell(2000)[17]利用双重差分法研究了美国俄亥俄州Shaker Heights1987年学区重组对房价的影响，结果表明，失去临近小学使房价下降约9.9%。李雪松等(2017)[18]利用双重差分法定量研究了“二孩”政策的出台对家庭教育资源需求和学区房房价的影响，结果表明“单独二孩”政策的出台使家庭对普通和优质教育资源的支付意愿分别增加了3.97%、11.8%。

综上所述，已有有关学区房溢价问题的研究，主要借助传统的特征价格模型，定量评估教育资本化效应，但是鲜有考虑教育政策这一对学区房房价产生重要影响的因素。在实证方法方面，普遍采用特征价格模型，一些学者用边界固定效应法和配对差分法消除部分不可观测因素的影响；在数据方面，越来越多的经验研究倾向于使用房屋微观交易数据；在研究结论方面，绝大多数研究都表明学校质量对学区房房价有显著的正向影响，教育资本化效应显著。对此，本文从教育政策视角出发，定量分析限制择校政策对学区房房价的影响，以便填补现有文献可能存在的不足。

三、模型构建与变量选取

(一)计量模型构建

1.特征价格模型

本文在实证第一阶段估计义务教育资本化效应，借鉴已有研究，构建特征价格模型：

lnPijkt=β0+β1schjk+β2Xijkt+β3Zijkt+β4Disk+β5Dt+μijkt

(1)

其中，下标i代表每一个房屋个体，j代表所处学区，k表示行政区，t代表交易发生的年份。核心解释变量为各小学质量(schjk)，其他特征变量包括：房屋物理特征变量(Xijkt)，房屋区位特征变量(Zijk)；Disk为行政区虚拟变量，Dt为年份虚拟变量；μijkt为随机误差项。此外，由于模型为半对数模型，故β1的含义为学校质量对于房价的边际影响率，即学校质量提高1单位，学区房单位价格上涨的比率(哈巍，2015)[7]。

因本研究整个数据集构成一组独立混合截面数据，每一条交易数据都是独立的个体，故而借鉴哈巍(2015)[7]的做法，采用混合OLS对模型进行估计，得到学校质量带来的学区房溢价的估计。

2.双重差分模型

实证第二阶段借助“通知”出台这一“准自然实验”，构建并估计双重差分模型。双重差分模型要求双重差分变量具有外生性，满足以下条件期望表达式：

E[εit|Treat,Xit]=0

(2)

其中，εit为随机误差项，Treat为双重差分变量，测度处理效应；Xit为控制变量。限制择校政策出台时间相对于学区房市场是外生的。同时，采用的数据是独立混合截面数据，数据集由独立抽取的观测值构成，可以满足残差项与分组变量完全独立[19]。因此，式(2)成立，研究具备采用双重差分法的条件。

双重差分模型(式(3))中，“通知”出台时间2014年1月是处理效应发生的节点，因此2012至2013年为T0期，2014至2015年为T1期；“省重点”和“市重点”小学统一视作重点小学，构成处理组，“普通”小学视作控制组。

lnPit=α0+α1Treat+α2Schooli+α3Dt+β1Xit+β2Zi+β3Disk+β4Tt+εit

(3)

其中Treat = DtxSchooli，为双重差分变量；Dt和Schooli分别表示时间和分组的虚拟变量；控制变量包括：房屋物理特征(Xit)和区位特征(Zi)、行政区虚拟变量(Disk)和年份虚拟变量(Tt)。

(二)变量选取与描述性统计

本研究样本观测期为2012年1月至2018年8月，使用的学区房交易数据主要通过爬虫方式获得，包含南京市四大主城区53所小学的8 988条二手学区房交易数据。学校质量数据来源于搜狐网、各学校官网上的信息。被解释变量为二手学区房单位面积价格(对数形式)。因二手房学区房价的市场化程度更高，故采用二手学区房单价[6]。利用官方统计年鉴中江苏省GDP平减指数，以2012年为基期，对后续年份的房价进行折算。

在特征价格模型中，核心解释变量为小学质量，度量方式有以下两种：一是以各小学2017、2018两年小升初考上南京外国语学校(简称“南外”)的学生数的均值度量。二是依据学校的等级，将“普通”小学作为基准变量，分别设置“省重点”和“市重点”两个虚拟变量。因学区房往往具有“双学区”特性，本文将住房对应的初中等级虚拟变量纳入模型，以综合衡量区域内义务教育水平。控制变量还包括：房屋物理特征：绿化率(green)、物业费(fee)、容积率(plot)、房龄(age)、装修程度(精装、简装、其他)；房屋区位特征：到最近地铁站的距离(d_sub)、到最近综合性医院的距离(d_hos)、到对应小学的距离(d_sch)、到市中心新街口地铁站的距离(d_CBD)。距离变量取对数。此外，模型中还添加了行政区虚拟变量和年份虚拟变量。

从表1数据描述性统计中可得：首先，不同等级的小学对应学区房单价有明显差别，省重点小学学区房单价均值高于市重点和普通小学。其次，各学校小升初被南外录取的学生人数均值为7(人)，“省重点”、“市重点”和“普通”小学被南外录取的学生数均值分别为11、4、0.02，可以看出教学质量的明显差别。最后，就其他特征变量而言，“省重点”小学物业费低于其他两类学校，房龄高于“市重点”和“普通”小学，这两项指标验证了现实中的情形，即重点学校学区房往往建筑年代较早，建筑面积小，小区物业成本低，与其高房价形成一种鲜明对比。

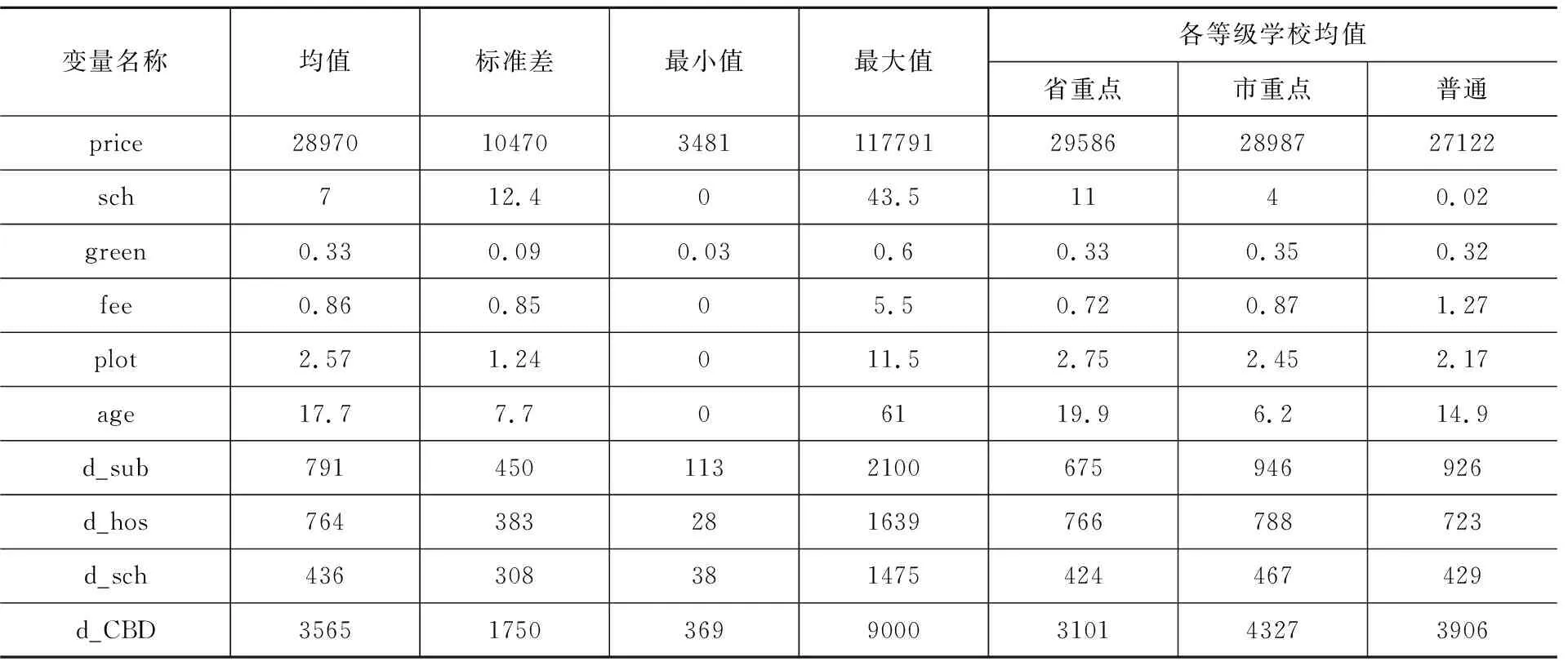
表1 连续型变量描述性统计

四、实证结果分析

本部分先利用整体样本进行回归，之后按行政区对4个子样本进行回归分析，以此考察南京市四大城区各自的学区房溢价情况。

(一)全样本特征价格模型估计结果

表2展示了用最小二乘法(OLS)对特征价格模型进行估计的结果。因随机扰动项存在异方差，采用稳健标准误差，结果如下：首先，模型1至4以小升初考上南外的学生数为核心解释变量，依次添加了控制变量。模型4中，小学质量系数估计值为0.012，初中质量系数估计值为0.09，二者均在1%的显著性水平上显著，表明在其他因素不变的情况下，对应小学考入南外的学生数增加1人时，学区房价格上涨1.2%；与“普通”初中相比，“重点”初中带来的学区房溢价幅度是9%。其次，模型5、6以小学等级虚拟变量为核心解释变量，模型6控制了其他因素的影响后，估计得到与普通小学相比，“省重点”小学将带来8.8%的学区房溢价，“市重点”小学学区房溢价8%，“市重点”小学学区房溢价略低于“省重点”小学。从消费者偏好角度分析可知，相对于普通小学，家庭更偏好于“省重点”与“市重点”小学。此外，与“普通”初中相比，“重点”初中将带来13%的学区房溢价，初中质量对学区房房价有显著的正向影响。最后，关于房屋特征变量，模型4表明，物理特征中，绿化率、物业费与房价成正比，容积率与房龄与房价成反比，容积率越高、房屋越老旧，带来的舒适度越低，房价也就越低；同时，精装修房屋价格更高，而简装会降低房屋售价。区位特征变量中，到地铁站和学校的距离的系数显著为负，说明到学校的距离越近，交通的便利性越高，房价越高；同时，到医院距离的系数为正且显著，原因可能是这一距离不是购房者或卖房者决策时首要考虑的因素。距离变量间存在一定的共线性，但总体而言，交通越便利，房价越高。

表2 全样本特征价格模型回归结果

(二)全样本双重差分模型估计结果

估计双重差分模型前，首先检验平行趋势假设(Parallel Paths)是否成立。以2014年第一季度为基期，将其他各季度与处理组的交互项和其他控制变量纳入模型，回归结果表明2012年、2013年各季度交叉项系数为负且不显著，说明政策出台前，处理组与控制组因变量趋势不存在明显差异，平行趋势假设成立。

以房价对数为被解释变量，估计双重差分模型，其中样本观测值总数为4 629个。由表3可知，与模型1、2相比，模型3加入时间和区域虚拟变量后，控制了研究期间一些其他政策和市场环境因素及区域间差异的影响，使得模型解释力增强，得到双重差分变量估计值为0.59，表明在控制了其他房价影响因素的情况下，2014年限制择校政策出台后，在教育资本化效应的基础上，与普通小学学区房房价相比，重点小学学区房受政策影响额外溢价5.9%，且这一数值在1%的显著性水平上显著，其他控制变量的系数估计值符合预期。

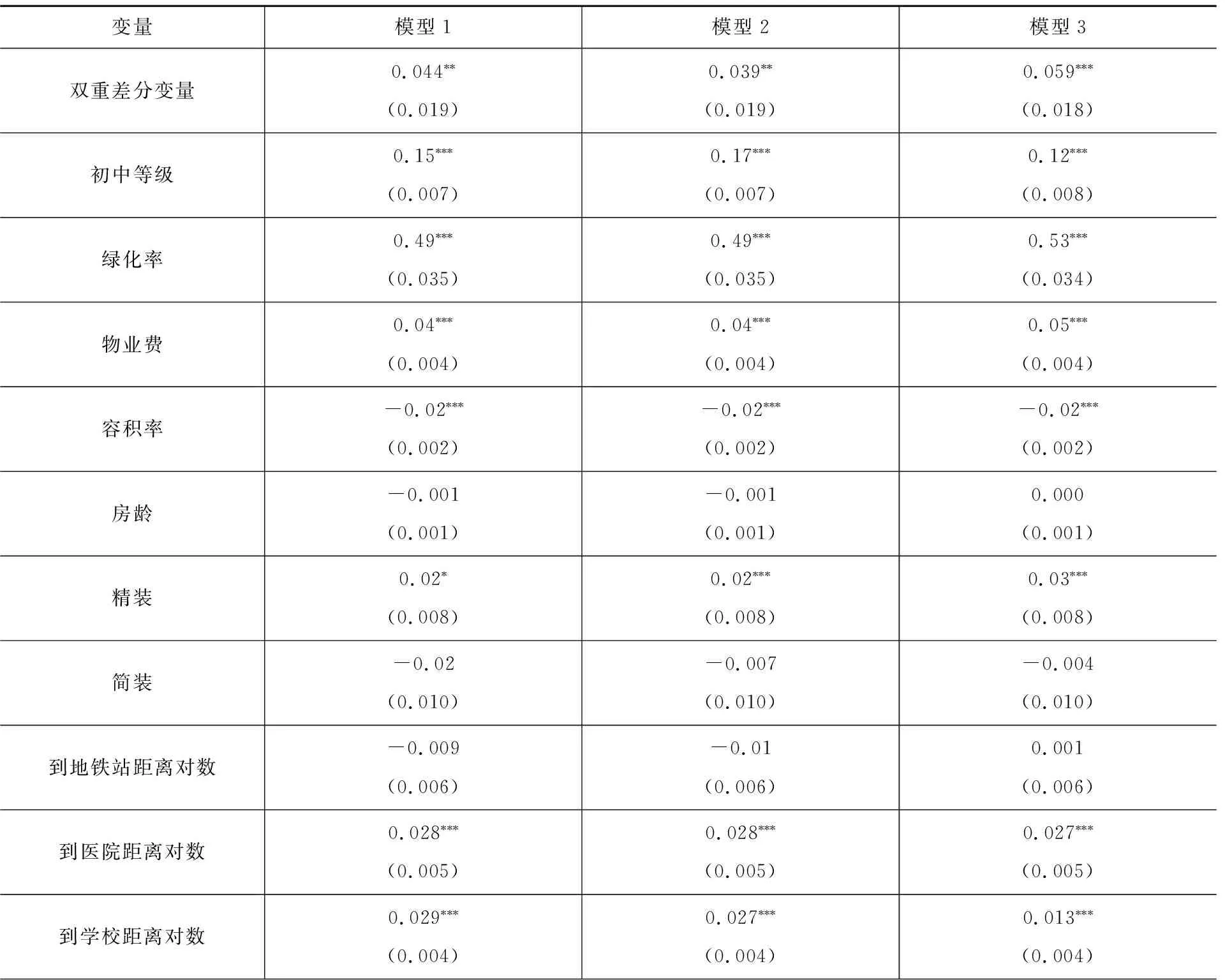
表3 全样本双重差分模型估计结果

这一结果表明限制择校政策确实对学区房市场产生了显著的影响，2014年限制择校政策出台后，通过强化“以房择校”，使得家庭对于重点小学学区房的需求增大了，导致重点小学学区房价格上涨快于普通小学学区房。表明就南京市四大城区而言，相对于普通小学，重点小学出现“天价”学区房的原因除了优质教育资源的资本化效应之外，还有限制择校政策的推动作用。从家庭支出的角度看，限制择校政策抬高了购买重点小学学区房的成本，由此在限制“择校费”、“特长生”等不公平竞争的情况下，又重新制造了另一种不公：居高不下的重点小学学区房房价意味着家庭投资教育的成本也不断增高，低收入家庭将因为难以负担高昂的“以房择校”费用而选择非重点学校。这一结论与宋伟轩等(2019)[20]研究结论相同。

(续表3)

(三)分区域特征价格模型估计结果

为对比考察不同行政区学区房溢价现象，分区域对特征价格模型进行估计。小学质量采用考上南外的学生数，鼓楼区、秦淮区、玄武区、建邺区小学质量取值分别是16.4、0.5、1.9、0.13。因房屋属性变量的系数估计值较符合预期，表4只汇报了核心解释变量估计结果。

由表4可知：首先，鼓楼、秦淮、玄武、建邺四区小学质量系数估计值依次是0.014、0.056、0.04、0.11，且在1%的显著性水平上显著，表明考入南外的学生数增加1人时，鼓楼、秦淮、玄武、建邺学区房房价分别上涨1.4%、5.6%、4%和11%，不同区域存在不同程度的教育资本化效应。其次，就初中等级虚拟变量系数估计值而言，鼓楼区为-0.035，且显著，这一结果可能是由小学质量与初中质量间的共线性导致的；秦淮、玄武和建邺区初中等级变量系数显著为正，说明小学质量与初中质量都对房价产生正向的影响，具有优质小学和优质初中教育资源的“双学区”学区房的教育资本化效应更显著。

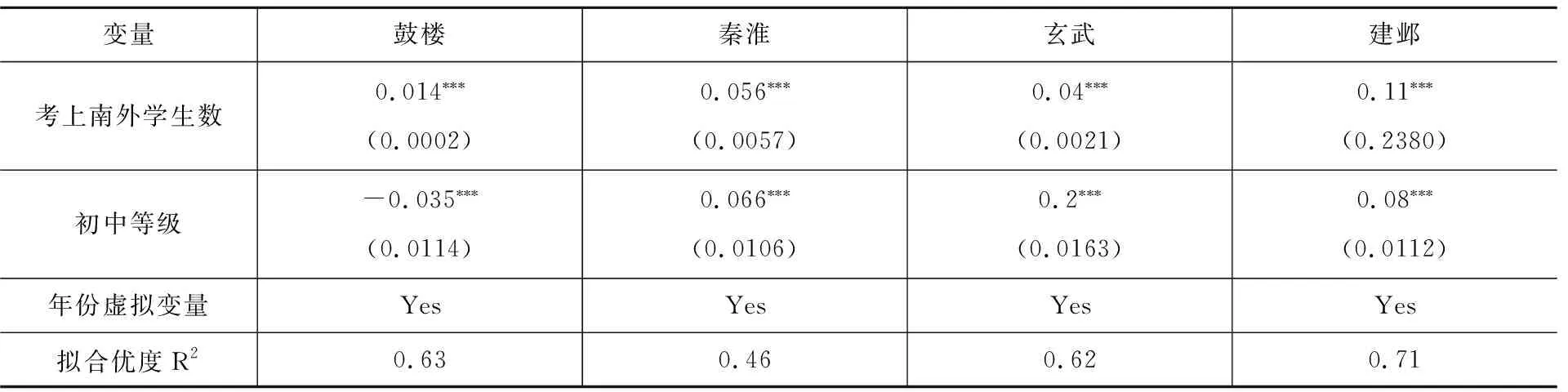
表4 分区域特征价格模型估计结果

(四)全样本双重差分模型估计结果

表5展示了各区域双重差分估计结果。舍去小学均为“省重点”或“市重点”的鼓楼区样本后，其他三区的实证结果分析如下：

表5 分区域双重差分模型估计结果

秦淮区双重差分变量系数估计值为负且显著，表明限制择校政策导致秦淮区重点小学学区房价格下跌5.1%，不符合上文的预测。这一结果可能是由秦淮区同时期其他政策因素抑制了重点小学学区房房价导致的，也与样本量不足有关；玄武区双重差分变量系数估计值为正但并不显著，建邺区双重差分变量估计值为0.067，显著为正。表明在建邺区，相对于普通小学，限制择校政策的出台导致重点小学学区房溢价6.7%，居民对重点小学的偏好与需求更为强烈。从上述结果可以看出，限制择校政策对于南京市不同行政区学区房房价的影响具有异质性。不同行政区学区房市场的不同表现可能与该区域经济发展情况、公共品提供、相关政策、群分效应等因素有关。

五、结论

本文旨在研究南京市限制择校政策对学区房房价的影响，以此回答限制择校是否促进了义务教育均衡化的问题。实证结果表明：限制择校政策确实对重点小学和普通小学学区房房价产生了异质性影响，导致南京市主城区重点小学学区房除学校质量带来的溢价外，相对于普通小学，价格额外上涨了5.9%。表明限制择校政策抬高了优质学区内房价，使得低收入家庭难以负担高昂的“以房择校”费用，从而不利于实现义务教育均衡发展。

要改变重点小学学区房高房价现象，促进义务教育均衡发展，需要进行政策的顶层设计，以最大限度降低城市内部教育资源的校际和群体间差距，增强教育资源配置的均衡性，主要有以下几方面：首先，实行区域内“多校划片”，使学区房产权不必然对应重点学校入学资格，为学区房“降温”；其次，弱化重点和非重点小学的等级区分，例如通过南京市的“集团化办学”、名校师资流动、教育政策及资源向薄弱学校倾斜等措施，缩小重点和普通小学之间的差距；再次，在义务教育系统中引入竞争，鼓励民办、外资小学发展，并全面实行“公民同招”。通过严格落实免试就近入学，电脑派位，全面取消特长生招生，禁止通过笔试面试、评测等方式招生，达到规范各学校招生行为的目的，喊停“掐尖”招生行为的同时进一步限制了家长择校行为，从而促进教育公平，也促使教育理念从传统的应试教育向素质教育转变。最后，从财政政策角度，应试行房产税政策，对于学区房溢价带来的资本收益征税，促进社会公平。