巧妙转化,化繁为简
———浅析指数函数f(x)=ex 在抽象函数中的应用
◇ 陕西 石 鹏 刘 卓
抽象函数是指没有给出具体解析式的函数,是高中数学函数中的一个重要研究对象.由于抽象函数可以全面考查学生对函数的定义域、单调性、奇偶性、对称性和周期性等性质的掌握,所以抽象函数在高考中常出现.本文对与指数函数的抽象形式有关问题的解法进行研究与总结.
1 在抽象函数单调性中的应用
例1已知函数f(x)满足:对任意的x,y∈R有f(x)·f(y)=f(x+y),且f(1)>1,则在区间[-2,2]上,自变量x取( )时,f(x)取得最大值.
A.-2 B.2 C.0 D.1或-1
解析
由于指数函数y=ax(a>0且a≠1)满足:对任意的x,y∈R有f(x)·f(y)=f(x+y),因为f(1)>1,不妨设函数f(x)=ex,易知f(x)在区间[-2,2]上单调递增,所以当x=2时函数f(x)取得最大值.故选B.
本题利用指数函数的特征,将抽象函数问题转化为显函数问题,直接利用指数函数y=ex的单调性,快速解决此类问题,避免了利用单调性的定义判断的步骤,从而使复杂问题简单化.因此,我们需要熟练掌握基本初等函数的抽象形式,才能达到灵活应用、融会贯通的目的.其他形式如下.
(1)常函数:f(x)=f(y);
(2)正比例函数:f(x)±f(y)=f(x±y);
(3)幂函数:f(x)·f(y)=f(xy),f(x)-
(4)对数函数:f(x)+f(y)=f(xy),f(x)-
2 在抽象函数不等式中的应用
例2已知定义在R上的函数f(x)满足:f′(x)>2f(x),且f(1)=1,则不等式f(x)>e2x-2的解集为( ).
A.(-∞,1) B.(1,+∞)
C.(-1,1) D.(0,1)
解析

由f′(x)>2f(x)知F′(x)>0,所以F(x)为R上的增函数.
f(x)>e2x-2,即,由f(1)=1可知,F(x)>F(1),所以x>1,故选B.
此题利用导数公式:(e2x)′=2 e2x,结合题干中的抽象函数不等式f′(x)>2f(x),构造抽象函数F(x),容易判断F′(x)的正负性,确定F(x)的单调性,然后将问题转化到构造的函数F(x),使问题简单明了.
与指数函数ex有关的抽象函数构造方法有:
(1)f′(x)+f(x)>0,构造F(x)=exf(x);
(2)f′(x)-f(x)>0,构造
(3)f′(x)+kf(x)>0(k>0),构造F(x)=ek xf(x);
(4)f′(x)-kf(x)>0(k>0),构造F(x)=
(5)kf′(x)+f(x)>0(k>0),构造F(x)=
(6)kf′(x)-f(x)>0(k>0),构造F(x)=
(7)(1+x)f(x)+xf′(x)>0,构造F(x)=xf(x)ex;
(8)(1-x)f(x)+xf′(x)>0,构造F(x)=
3 在抽象函数等式中的应用
例3设函数f(x)满足x2f′(x)+2xf(x)=,则x>0时,f(x)( ).
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
解析
因为(x2f(x))′=x2f′(x)+2xf(x),设g(x)=x2f(x),则,且f(x)=,所以
记h(x)=ex-2g(x),则h′(x)=ex-2g′(x)=,所以当x∈(0,2)时,h′(x)<0,h(x)在(0,2)上单调递减;当x∈(2,+∞)时,h′(x)>0,h(x)在(2,+∞)上单调递增.因此h(x)≥h(2)=e2-2g(2)=e2-8f(2)=0,即x∈(0,+∞)时,f′(x)≥0,所以f(x)在(0,+∞)单调递增,故f(x)在(0,+∞)上既无极大值也无极小值.故选D.
例4已知函数f(x)的导函数为f′(x),且对任意的实数x都有f′(x)=e-x(2x+3)-f(x)(e是自然对数的底数),且f(0)=1,若关于x的不等式f(x)-m<0的解集中恰有2个整数,则实数m的取值范围是( ).
A.(-e,0] B.[-e2,0)
C.[-e,0) D.(-e2,0]
解析
由f′(x)=e-x(2x+3)-f(x),可知(f′(x)+f(x))ex=2x+3,即

所以exf(x)=x2+3x+C(其中C为常数),所以.由f(0)=1,可知C=1,所以,则

故f(x)的增区间为(-2,1),减区间为(-∞,-2)和(1,+∞),且有f(-2)=-e2,_________________的图象如图1所示,f(-1)=-e,f(-3)=e3.

图1
综上,不等式m>f(x)的解集中恰有2个整数,这2个整数只能是-2,-1,所以m∈(f(-1),0],即m∈(-e,0].故选A.
上述两道例题条件的一般形式为定义在D上的函数f(x)满足:f′(x)g(x)+f(x)g′(x)=h(x),且f(x0)=m,然后判断函数f(x)的单调性.
解题思路由题意知(f(x)g(x))′=h(x).
① 若存在函数H(x),使得H′(x)=h(x),则f(x)g(x)=H(x)+C(其中C为常数),f(x)=,由f(x)=m,解得C=C,于是函数00f(x)的解析式确定.
② 若不存在函数H(x),使得H′(x)=h(x),令F(x)=f(x)g(x),则F′(x)=h(x),所以f(x)=,所以


于是使得G′(x)不是抽象函数,且可判断G′(x)的正负性,从而判断G(x)的单调性,结合f(x0)=m与可判断函数f′(x)的正负性,从而判断函数f(x)的单调性.
4 在与抽象函数有关的数列中的应用
例5已知函数y=f(x)的定义域为R,当x<0时,0<f(x)<1,且对任意的x,y∈R,等式f(x)·f(y)=f(x+y)成立,若数列{an}满足f(an+1)·,且a1=f(0),则下列结论成立的是( ).
A.f(a2016)<f(a2019) B.f(a2017)<f(a2020)
C.f(a2018)<f(a2020) D.f(a2018)<f(a2019)
解析
由任意的x,y∈R,等式f(x)·f(y)=f(x+y)成立和当x<0时,0<f(x)<1,不妨设f(x)=ex,所以

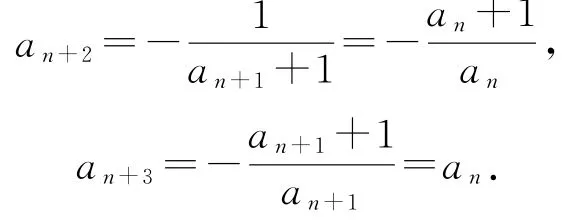
所以,数列{an}是以3为周期的周期数列,
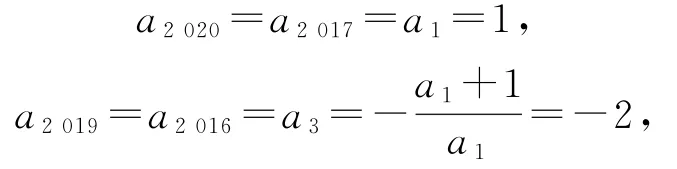
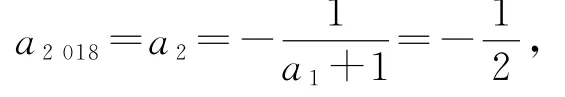
所以a2020>a2018>a2019,f(a2020)>f(a2018)>f(a2019),故选C.
本题利用抽象函数构造数列,将数列的周期性与函数的单调性综合考查,根据抽象函数递推式,将抽象函数转化到指数函数y=ex,使得抽象函数的单调性简单明了,再借助指数运算容易给出数列的递推关系式,从而得到数列的周期性,使问题得以解决.
5 在抽象函数导数与数列中的应用
例6已知定义在R上的函数f(x),g(x)满足:对任意的x,y∈R都有f(x)f(y)g(x+y)=g(x)g(y)f(x+y),且f′(x)g(x)>f(x)g′(x),e(f(1)g(-1)+f(-1)g(1))= (e2+1)g(1)·g(-1),数列{bn}满足:f(n)=bn·g(n),则数列{bn}的前10项和为( ).

解析
对任意的x,y∈R,有

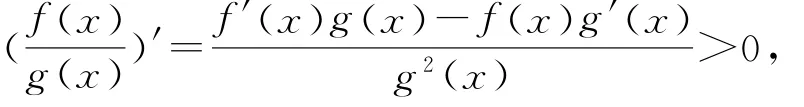
由e(f(1)g(-1)+f(-1)g(1))=(e2+1)·g(1)g(-1)可知解得a=e或(舍),所以,即{bn}为等比数列,前10项和为,故选C.
求解此题的关键是将抽象函数的一般形式向指数函数的抽象函数形式转化,结合导数运算确定单调性,从而解得数列的通项公式.
指数函数作为高考数学的一个重点考查对象,在函数中有着举足轻重的地位.当遇到对任意的x,y∈R有f(x)f(y)=f(x+y)的模型时,就可以向指数函数y=ax(a>0且a≠1)上转化,从而使问题得以简化,达到化繁为简的目的.

