圆锥曲线问题融入“心”中

◇ 重庆 何朝枢

三角形的“四心”(垂心、重心、内心、外心)具有各自不同的几何定义与性质,而在圆锥曲线问题中巧妙融合入三角形的“心”,是一类既富交会性、思考性和挑战性,又具有一定难度和深度的数学问题,在近年的高考中时常出现,是考查学生的思维方式和数学能力的一个好方式．

1 圆锥曲线问题融入“垂心”

例1在平面直角坐标系x Oy中,已知椭圆C：的焦距为2,且过点

(1)求椭圆C的标准方程；

(2)设椭圆C的上顶点为B,右焦点为F,直线l与椭圆交于M,N两点,问是否存在直线l,使得F为△BMN的垂心．若存在,求出直线l的方程；若不存在,说明理由．

解析(1)由题目条件可得a2＝b2＋c2,解得a2＝2,b2＝1,所以椭圆C的标准方程为

(2)假设存在直线l满足题设条件,即直线l与椭圆交于M,N两点,且F为△BMN的垂心．

如图1所示,由(1)可得B(0,1),F(1,0),则有,由于点F为△BMN的垂心,则有BF⊥直线l,可得kl＝,可设直线l的方程为y＝x＋m,设M(x1,y1),N(x2,y2),联立消去参数y并整理可得3x2＋4mx＋2m2－2＝0．

图1

2 圆锥曲线问题融入“重心”

例2已知点A,B,C为椭圆上三个不同的点,O为坐标原点,若2则△ABC的面积为( )．

解析

当直线AB的斜率存在时,可设直线AB的方程为y＝kx＋m,设A(x1,y1),B(x2,y2),代入椭圆方程x2＋2y2＝2,消去y并整理可得(1＋2k2)x2＋4kmx＋2(m2－1)＝0．根据根与系数的关系,可得

设C(x3,y3),由于,可得x3＝,将点C(x,y)代入椭圆方程33x2＋2y2＝2,整理可得1＋2k2＝4m2,而根据弦长公式有到直线AB的距离,则有结合三角形的重心的几何意义与性质,可得S△A B C＝；根据选择题的唯一性,当直线AB的斜率不存在时不加以具体分析,此时也可得．故选C．

3 圆锥曲线问题融入“内心”

例3已知F1,F2分别为椭圆(a＞b＞0)的左、右焦点,求椭圆C的离心率e为,点P是椭圆C上除长轴顶点外的任意一点,而△PF1F2的内切圆的圆心为I,设直线IF1,IF2的斜率分别为k1,k2,则k1k2＝________．

解析

设△PF1F2的内切圆的圆心I在三角形的对应三边上的投影分别为D,E,H,根据三角形的内心的几何意义与性质,设|F1D|＝|F1H|＝m,|F2D|＝|F2E|＝n,|PE|＝|PH|＝p,内切圆的半径为r,如图2所示．

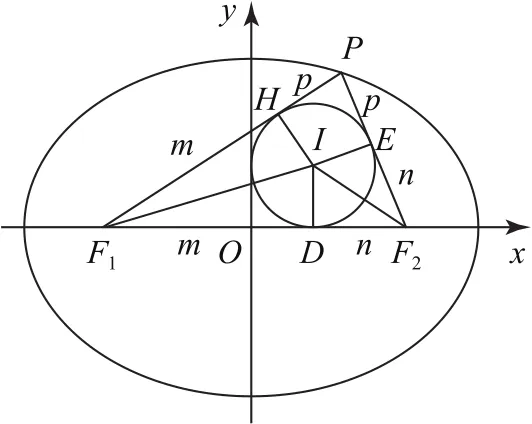
图2

利用椭圆的定义,可得|PF1|＋|PF2|＝m＋n＋2p＝2a,又|F1F2|＝m＋n＝2c,则有p＝a－c,结合海伦公式可得△PF1F2的面积为S＝,结合三角形的内切圆的性质可得△PF1F2的面积为S＝(m＋n＋p)r,那么

整理有mnp＝(m＋n＋p)r2,结合图形直观,可得

同时要注意对应问题中三角形的“心”的表达方式与“心”的名称,正确区分各“心”的性质及其结构特征,再结合圆锥曲线的相关知识加以合理应用．合理融入“心”,增加问题的交会性,让学生真正领悟到数学的和谐之美．