疏油改性对玻纤聚结元件气液过滤性能的影响

刘宇峰，姬忠礼，陈锋，刘震，常程

（中国石油大学（北京）机械与储运工程学院，过程流体过滤与分离技术北京市重点实验室，北京102249）

引 言

聚结元件在压缩空气过滤、气体长距离输送、密封气过滤和金属切割等领域具有广泛的应用[1-2]，气体中的液滴杂质若不能被及时分离，将会损坏下游仪器设备、腐蚀输送管道或者危害工人的身体健康。对于气体中小液滴的去除，聚结分离是最为有效的方法之一。而纤维滤材作为聚结过滤器的核心组成部分，其气液聚结分离过程较为复杂，过滤分离性能的影响因素较为广泛[3]。

目前，国内外学者在滤材压降和效率模型[4-5]、滤材和液滴物性[4,6-7]等因素上做了大量研究。Contal 等[6]根据各个阶段液体在滤材中分布情况将液滴聚结过程分为缓慢增加阶段、指数增长阶段、急剧增长阶段和稳定阶段。Frising 等[8]对此进行实验研究，根据四个阶段液滴在纤维中润湿和迁移情况，改进了压降和穿透率模型。除了宏观参数影响，液滴在纤维上的分布形态及受力情况等微观分析对于聚结机理研究也尤为重要。由于润湿性的不同，液滴在单根纤维上有液膜、桶形液滴及蛤壳形液滴三种不同接触形态[9]。Mullins 等[10-11]对亲、疏油单根纤维上液滴运动进行微观分析，发现疏油纤维上的蛤壳形液滴更易发生振荡，稳定性较差，易与纤维分离。上述研究表明，滤材的润湿性在微观层面影响液滴与纤维的接触形态，从而影响液滴的聚结过程。因此，对于纤维滤材润湿性的研究具有重要意义。

由于寻找结构参数相同、仅润湿性不同的两种商用滤材较难，国内外学者选用结构参数不同的亲、疏油型滤材进行对比[12-13]，研究滤材润湿性对过滤性能的影响。通过对比不同层数亲、疏油型滤材的压降，提出了“跳跃-通道”压降模型，结合毛细管理论对亲、疏油型滤材压降不同的原因进行了解释[14-15]。另外，润湿性影响液体在滤材内分布及受力情况[16]，从滤材下游穿透率[17]以及二次夹带[18]两个方面影响滤材过滤效率。对于粒子穿透率，通过对不同的亲、疏油型滤材进行实验研究，结合液体在滤材内部运移情况对亲、疏油型滤材穿透率不同的原因进行了解释[19]。对于二次夹带，Wurster 等[20-21]对亲、疏油型滤材的二次夹带现象进行定量检测对比，发现两者规律有较大不同。常程等[22]针对聚结滤芯的二次夹带现象进行研究，认为滤芯的表面润湿性对二次夹带有重要影响，亲油型滤芯更易出现二次夹带，进而影响其过滤效率。然而，上述研究无法排除结构参数的影响，难以控制变量对润湿性的影响。

综上所述，滤材润湿性通过影响液滴在纤维上的捕集、聚结及排液过程而使得滤材压降、穿透率等情况发生改变，滤材润湿性的差别是由于表面能不同所导致，研究滤材表面能有助于深入认识聚结机理，可为减小滤材持液率，研制低阻高效聚结元件提供指导。然而，目前对于单一表面能因素影响聚结元件过滤性能的研究较少。为此，本文采用不同浓度的改性溶液通过化学覆膜的方法对亲油型玻璃纤维滤材进行处理，在控制其平均孔径、纤维直径、透气性等结构参数几乎不变的情况下，得到表面能不同的改性滤材，将表面能作为单一变量进行研究，分析其对滤材压降、穿透率、二次夹带的影响及原因，并对此改性方法在聚结滤芯上的应用效果进行了研究。

1 实验材料和方法

1.1 材料及表征

选用亲油型玻璃纤维滤材，记为GF。采用目前国际测试标准中常用的癸二酸二辛酯（DEHS）作为实验液体，常温下不易挥发，密度为912 kg/m3，动力黏度为0.023 Pa·s。为分析不同表面能改性对滤材气液过滤性能的影响，使用不同浓度的氟硅氧烷丙烯酸酯共聚物水溶液通过浸渍法对亲油型玻璃纤维滤材GF 进行处理，得到改性滤材GF1～GF6。用瑞典BiolinScientific 公司Attension接触角测量仪，分别以水和DEHS 为介质，使5 μl 液滴自由落下与滤材表面接触，测得液滴与滤材表面接触瞬间的接触角[22]，每组选择滤材不同位置测量5 次取平均值。用美国Quantachrome 公司Porometer 3G 孔径测试仪测量滤材的平均孔径，每种滤材测量3次取平均值，结果见表1。

表1 滤材物性参数Table 1 Properties of experimental filter materials

利用日本日立公司SU8010 型扫描电镜观察滤材微观结构，结果如图1所示。由图可见，改性滤材GF1 的纤维形态未发生明显变化，仅在纤维连接处及纤维表面的粗糙度较未处理滤材GF 纤维的光滑表面有所增加。用FEI 公司Quanta 200F 场发射环境扫描电镜能谱系统分析其元素变化，如图2所示。由图可见，处理后滤材表面氟元素含量较未处理滤材增加了约1.5 倍，氟元素的存在降低了纤维的表面能。由于低表面能和粗糙度增加的耦合作用，处理后的滤材具有良好的疏水疏油性质。

图1 滤材微观结构的SEM照片Fig.1 SEM micrographs of filter material structure

由于聚结滤芯与实验滤材的气流方向有所不同（滤芯为柱形，气流方向一般为内进外出，即由下端口进气到柱形内部空间，之后气流沿斜上方向通过滤材；而滤材实验中气流水平通过滤材），实际应用中的滤芯性能可能与实验滤材性能存在差异。因此，本文对改性在滤芯上的实际应用效果进行研究。由于制作滤芯成本较高、工期较长，因此，本文先对不同表面能的滤材进行研究，再用改性滤材制作滤芯进行验证。选用亲油型玻璃纤维滤材GF，制作尺寸为φ62 mm×140 mm、层数分别为4、6、8 层的聚结滤芯，记为F4、F6、F8。选用改性滤材GF1，并制作尺寸为φ62 mm×140 mm、层数分别为4、6、8 层的改性滤芯，记为FN4、FN6、FN8。

1.2 实验装置及过滤性能评价

如图3 所示，利用美国TSI 公司气溶胶发生器9306A 产生DEHS 雾化液滴，保持上游气流中液滴浓度和粒径分布稳定，气体含液浓度700 mg/m3，在下游真空泵负压作用下，与洁净空气混合，水平通过直径150 mm 垂直放置的圆盘型滤材或气流方向内进外出通过尺寸为φ62 mm×140 mm 的待测滤芯。在下游设置美国Alicat Scientific 公司MCR 500 slpm质量流量控制器控制管道流量，以保持通过滤材表观气速为0.12 m/s。利用美国TSI 公司扫描电迁移率粒径谱仪（SMPS）和空气动力学粒径谱仪（APS）测量滤材上下游气流的液滴浓度和粒径分布，总测量粒径范围为0.05～20 μm。利用差压变送器对滤材两端压降进行连续测量记录。当压降和下游气流的液滴浓度基本保持不变时，认为过滤达到稳定状态[23]。过滤过程中的压降称为过程压降。实验开始前和结束后，利用瑞士Mettler Toledo 公司电子分析天平（AL204-IC）对滤材进行称重，用于计算滤材饱和度。实验测试仪器参数见表2。为验证实验系统的稳定性，对3 组相同的GF 滤材进行过滤测试，计算3次测量的相对标准差，验证上、下游气溶胶液滴浓度及压降的重复性。3 组滤材的上、下游气溶胶液滴浓度和稳态压降的相对标准差分别为0.62%、0.27%和1.6%。

聚结元件的过滤性能主要由压降和过滤效率决定。过滤效率较高的聚结元件一般压降也较高，引入同时考虑压降及过滤效率影响的品质因子[24]综合评价其性能。

品质因子QF计算公式为

式中，Cin和Cout分别为上游和下游气流中液滴的计数浓度，#/cm3；Δp为过滤介质压降。饱和度S计算公式为

式中，moil为过滤介质内部油的质量，kg；moil,max为过滤介质内部能够容纳的最大油质量，kg；mfilter和mfilter,0分别为过滤介质稳态质量和初始质量，kg；V为过滤介质体积，m3；ρoil为油的密度，kg/m3；α 为过滤介质填充密度。

图3 过滤性能实验装置Fig.3 Filtration performance experimental set-up

2 实验结果与讨论

2.1 改性对滤材过滤性能的影响

2.1.1 改性对滤材压降的影响 滤材是聚结元件的核心组成部分，为分析疏油改性对滤材过滤性能的影响，控制滤材结构参数不变的情况下对滤材GF进行改性，得到不同表面能滤材GF1～GF6，其对水和DEHS 的接触角变化趋势如图4。图5 为滤材的压降对比，改性滤材GF1～GF6 相比滤材GF 稳态压降降低幅度在12%～34%之间，改性滤材在相同实验条件下更快达到稳定状态。

图4 滤材对水和DEHS的接触角Fig.4 Contact angle of the material to water and DEHS

以改性滤材GF1 为例，分析改性对滤材压降的影响，在相同实验条件下，对未处理滤材GF 和改性滤材GF1 的初始压降、过程压降和稳态压降进行对比。如图5 所示，改性处理对滤材初始压降影响较小，但是降低了滤材的稳态压降。为分析滤材压降变化的原因，对过滤过程中的液滴进行受力分析，液滴在水平气流方向受到气流的曳力Fd，滤材孔隙形成的毛细管对液滴的毛细管阻力P和液滴在滤材通道间运移受到的运动阻力Fr。根据克服的阻力不同，将稳态压降分为克服P 导致的跳跃压降和克服Fr导致的通道压降两部分进行讨论。

如图6 所示，滤材GF1 相比滤材GF 跳跃压降明显减小，是造成滤材GF1 稳态压降小的主要原因。跳跃压降与液体进入或离开纤维滤材所克服的毛细力相关[15]。分析认为，所克服毛细管阻力P 是液滴与形成毛细管的纤维接触界面之间的附着力和液滴分子的内聚力的合力。附着力和内聚力的大小比较决定了纤维滤材的毛细管对液滴作用力是牵引或排斥。Washburn[25]基于圆柱型毛细管与液滴的界面附着力和内聚力提出毛细管压力公式

式中，γ为液体表面张力，N/m；r为毛细管半径，m；θ为液滴接触角。

Mullins 等[26]对平均纤维直径＜5 μm 的薄玻璃纤维滤材提出等效毛细管半径模型

式中，rc为滤材等效毛细管半径，α 为滤材填充密度，rf是纤维半径。将式（4）代入式（3），得出玻璃纤维滤材毛细管阻力

图5 滤材压降对比Fig.5 Comparison of pressure drop for filter materials

可知，毛细管阻力P 与液滴表面张力γ、滤材填充密度与纤维半径的比值α/rf和液滴与滤材接触角θ相关。而本实验中液滴的表面张力γ不变，且改性后滤材填充密度与纤维半径的比值α/rf不变。DEHS 液滴在滤材GF、GF1 上的接触角分别为39.89°和121.40°,可知|cos θGF|＞|cos θGF1|。因此，改性后滤材GF1 毛细管阻力数值减小。滤材GF 与滤材GF1的毛细管阻力方向相反，滤材GF毛细管力阻止液体离开，在滤材后表面形成液膜，而滤材GF1毛细管力阻止液体进入，在滤材前表面形成液膜，滤材的跳跃压降与形成的液膜相关。这也是图6中滤材GF的跳跃压降在后，而滤材GF1的跳跃压降在前，且改性滤材GF1跳跃压降数值较小的原因。

图6 滤材压降划分及下游粒子浓度Fig.6 Pressure drop division and downstream particle concentration for filter materials

此外，由于滤材中的毛细孔道是各向随机分布的，纵向也同样存在毛细管力，而滤材GF 的纵向毛细管力对液滴有吸附作用，液滴需要聚合到其重力足以抵消纵向毛细管力时才可以排下，加剧了滤材GF后表面液膜的形成。此过程可由滤材饱和度（图7）证明，在实验结束后，滤材表面形成的液膜被吸附在滤材上而导致了滤材饱和度的升高，滤材GF的饱和度明显高于滤材GF1，说明其形成液膜的含液量高于滤材GF1，导致滤材GF的跳跃压降较高。

通道压降与液滴从厚度方向通过整个滤材并行通道所受到的阻力Fr相关。液滴在亲油和疏油纤维上分别呈膜状分布和滴状分布[27]，如表1 所示，纤维间的等效孔道直径只有10 μm 左右，如图8（a）、（d）所示，对于滤材GF1，在纤维上呈滴状分布的微米级液滴比膜状分布的薄液膜占据纤维间孔道更多的体积，使得气体流道更加曲折，增加了气流通过流道的阻力Fr，故滤材GF1的通道压降较高。因此，对滤材的疏油改性处理减小了其跳跃压降，虽然小幅增加了通道压降，但仍减小了滤材的稳态压降，这意味着改性后滤材在使用过程中有更低的能耗。

图7 滤材饱和度对比Fig.7 Comparison of saturation for filter materials

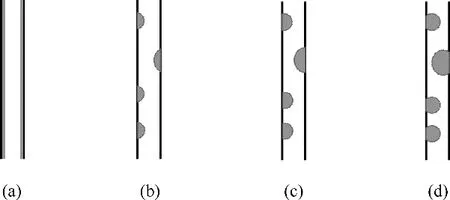
图8 液滴在滤材孔隙组成的毛细管中的形态Fig.8 Droplets morphology in capillary composed of filter materials pores

对于不同表面能的疏油改性滤材，如图5所示，滤材GF1～GF6 之间跳跃压降相差较小，图7 显示其饱和度也相差较小，但改性滤材的跳跃压降和饱和度都比未处理滤材GF 小近40%。跳跃压降和饱和度趋势相近的原因是单层滤材在实验过程中由于克服毛细力而形成的液膜在实验结束后仍然吸附在滤材上。如图5 所示，滤材GF1～GF6 的通道压降先减小后增加，由于GF1～GF6的纤维表面能先增加后减小（图4），因此，滤材的通道压降随纤维表面能的减小而增大。分析认为，随着纤维表面能的减小，由于体系Gibbs 自由能趋向于减小，液滴越收缩趋向于球形，接触角越大，图8为液滴在纤维表面能逐渐减小的滤材孔道中的形态，孔道中的微米级液滴接触角越大，液滴在纤维上滴状分布的高度越高，占据纤维间孔道的截面面积越大，使得气体流道越曲折，气流通过流道的阻力越大，即滤材的通道压降越高。因此，对于结构参数相同的疏油滤材，随着纤维表面能的减小，滤材通道压降增加，稳态压降也随之增加。

图9 滤材过滤效率对比Fig.9 Comparison of filtration efficiency for filter materials

2.1.2 改性对滤材效率的影响 图9（a）为滤材对0.05～0.5 μm 液滴的累积计数效率对比，改性滤材相比未处理滤材对0.05 μm 以上液滴的稳态过滤效率从87.24%提高到95.85%以上，并且随着滤材纤维表面能的减小，其对0.05 μm 以上液滴的过滤效率逐渐升高。分析认为，对于粒径＜0.5μm 的小液滴，主要由扩散作用被纤维拦截[3]。纤维对颗粒的扩散分离效率与颗粒运动黏度、运动速度、纤维填充密度、纤维直径、纤维有效过滤面积等参数相关[28]。随着纤维表面能的减小，液滴在纤维上的接触形态由膜状铺展变为滴状分布，由于疏油滤材的纤维表面能较液滴更小，体系Gibbs 自由能趋向于减小，液滴收缩成球形，表面减少，而纤维表面增加，纤维有效过滤面积变大，所以纤维扩散拦截作用更强[19]；且液滴越难润湿纤维，纤维越洁净，液体越难在纤维间形成液桥和液膜，气流通过洁净纤维时更有机会因扩散作用而被纤维拦截。图10为实验后滤材GF 和GF1中液体分布的电镜照片，在滤材GF的纤维间可以看到明显的液桥和液膜，由于小液滴的气体跟随性较好，而大部分气流从液膜间的空隙流过，故液膜的存在减小了气流中小液滴与纤维接触的面积；而改性滤材GF1 则较为洁净，气流通过这些洁净纤维时更有机会因扩散作用而被纤维拦截，所以对0.05～0.5 μm液滴的过滤效率更高。

另外，在纤维表面对油具有高排斥性的时候，小油滴可以看作弹性小球，当油雾穿过滤材内部纤维层时，小油滴会在对油具有高排斥性的纤维之间弹跳碰撞[29]，聚成大油滴而后被纤维拦截，弹跳碰撞过程增加了液滴被捕集的概率。

图9（b）为滤材对0.5～20 μm 液滴的累积计数效率对比，改性滤材相比未处理滤材对0.5 μm 以上液滴的稳态过滤效率从99.28%提高到99.93%以上，并且随着滤材纤维表面能的减小，其对0.5 μm 以上液滴的过滤效率逐渐升高。分析认为，对于粒径＞0.5 μm 的大液滴，主要由惯性碰撞作用被纤维拦截[3]。随着纤维表面能的减小，液滴在纤维上由膜状分布变为滴状分布。纤维间的等效孔道直径只有10 μm 左右（表1），如图8 所示，孔道中的微米级液滴越趋于球形，液滴在纤维上的高度越高，占据纤维间孔道的截面面积越大，使得气体流道越曲折，越利于0.5 μm 以上液滴的惯性分离。因此，对于结构参数相同的滤材，其对液滴的扩散、惯性分离作用随表面能的减小而增强，故其过滤效率随表面能的减小而升高。

另外，在图9（b）中，滤材GF在液滴粒径1～2 μm处的效率有所降低，其原因是气流的剪切力使滤材后表面的液膜破裂[22]，造成夹带。夹带液滴粒径范围主要集中在1～2 μm，与Wurster 等[21]对聚结滤材夹带液滴粒径范围的研究结果相一致。而改性滤材GF1～GF6在此处效率提高较多，其原因是液滴从其前表面进入需克服毛细力，液膜形成在滤材前表面，气流的剪切力使液膜破裂所造成的液滴夹带仍有可能被滤材内部纤维所拦截。因此，对滤材的疏油改性增强了对液滴的扩散、惯性分离作用，减小了二次夹带，因而提高了滤材的过滤效率。

图10 实验后滤材的SEM照片Fig.10 SEM micrographs of filter materials after experiments

为分析滤材综合过滤性能变化，对比滤材压降及下游粒子计数浓度的变化趋势，如图6所示，滤材GF液膜形成阶段是粒子穿透率最高的阶段，分析认为，滤材后表面的排液薄膜在气流作用下形成气泡，其破碎产生碎片液滴[30]使得穿透率增加。而滤材GF1 下游浓度则一直下降，最后维持在较低水平，远远低于滤材GF。因此，对滤材的疏油改性可降低滤材稳态压降，同时提高滤材过滤效率，提升其综合过滤性能。

2.1.3 改性对滤材品质因子的影响 为分析改性对滤材综合过滤性能的影响，对滤材的品质因子进行计算，结果如图11所示。改性处理后滤材的品质因子均有所增加，对于＞0.05 μm 液滴的品质因子增加幅度在85%～136%之间，对于＞0.5 μm 液滴的品质因子增加幅度在93%～124%之间。改性滤材GF1～GF6 的品质因子随着滤材表面能的增加而增加，表面能最大的改性滤材GF4 的品质因子最高，虽然其过滤效率较其他改性滤材有小幅降低，但是其稳态压降较小，仍使其具有最佳的综合过滤性能。

2.2 改性在聚结滤芯上的应用

图11 滤材品质因子对比Fig.11 Comparison of quality factor for filter materials

图12 滤芯过程压降对比Fig.12 Comparison of process pressure drop for filters

2.2.1 改性对滤芯压降的影响 为验证改性在聚结滤芯上的应用效果，分别用未处理滤材GF 和改性滤材GF1 制作4、6、8 层的未处理滤芯F4、F6、F8和改性滤芯FN4、FN6、FN8，在相同实验条件下对其压降和稳态效率进行对比。图12 为滤芯过程压降对比，表3为滤芯初始、通道、跳跃、润湿及稳态压降对比。改性处理对滤芯初始压降影响较小，滤芯的初始压降、稳态压降及达到稳态所需时间均随层数增加而增大。滤芯F4、F6、F8跳跃压降相差较小，其原因在于跳跃压降代表着气流穿过液膜时克服的泡点压力，其数值由滤材的毛细作用力决定，由于本文滤芯使用同种滤材，无论层数多少，其跳跃压降数值相近。所以，稳态压降的差别主要体现在通道压降，随层数的增加而增大，其原因是在于通道压降代表气流通过滤材并行通道受到的阻力，其数值上取决于通道长度。

改性滤芯FN4、FN6 较未处理滤芯F4、F6 稳态压降分别降低10%和5%，从8 层开始，改性滤芯FN8 稳态压降高于未处理滤芯F8。可见改性滤芯较未处理滤芯的压降降低效果随滤芯层数的增加而减弱，分析认为，如2.1.1 节中所述，改性滤材较未处理滤材压降的降低主要体现在跳跃压降的大幅降低上，而通道压降反而有小幅升高。而滤芯层数的增加不会影响液滴进入或离开滤材表面所克服的毛细力，故多层改性滤芯跳跃压降的降低效果是不叠加的；随着滤芯层数的增加，相当于通道长度增加，气流通过滤材并行通道受到的阻力随通道长度线性增加，故多层改性滤芯通道压降的升高效果是随层数增加而叠加的。如表3 所示，随层数的增加，改性滤芯多层通道压降的升高逐渐抵消了滤芯表面跳跃压降的降低，从8 层开始，改性滤芯通道压降升高的数值超过了跳跃压降降低的数值。

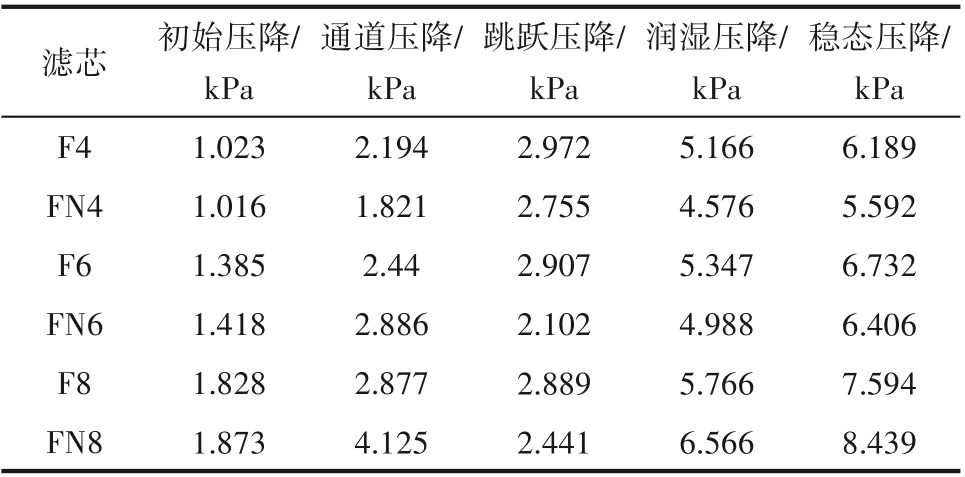
表3 滤芯压降对比Table 3 Comparison of pressure drop for filters

2.2.2 改性对滤芯效率的影响 图13 为滤芯的稳态累积计数效率对比。改性滤芯FN4、FN6、FN8 相比滤芯F4、F6、F8 对＞0.05 μm 液滴的稳态效率分别从99.061%、99.324%和99.935%提高到99.967%、99.949%和99.955%。改性滤芯FN4、FN6、FN8相比滤芯F4、F6、F8 对＞0.5 μm 液滴的稳态效率分别从99.944%、99.814% 和99.978% 提 高 到99.999%、99.999%和99.996%。改性滤芯稳态效率提高的原因与滤材同理。值得注意的是，随着层数的增加，未处理滤芯对小液滴（＞0.05 μm）的稳态效率有明显的升高，而对大液滴（＞0.5 μm）的稳态效率变化无明显规律，其原因是小液滴主要靠扩散作用分离，随着层数的增加，用于捕集液滴的有效纤维面积增加，故效率升高；而大液滴主要靠惯性作用分离，层数的增加对气流通过纤维间隙的速度无明显影响，所以对大液滴的惯性分离作用无明显影响，另外，气流通过亲油型滤芯后表面的液膜时易产生二次夹带，故层数增加对大液滴效率的影响无明显规律。

2.2.3 改性对滤芯品质因子的影响 图14 为滤芯的稳态品质因子对比。改性滤芯FN4 相比滤芯F4对＞0.5 μm 和＞0.05 μm 液滴品质因子分别增加了70%和90%，改性滤芯FN6 相比滤芯F6 对＞0.5 μm和＞0.05 μm 液滴品质因子分别增加了92%和59%，改性滤芯FN8相比滤芯F8对＞0.5 μm和＞0.05 μm液滴品质因子分别增加了8%和减小了6%。

综上所述，改性滤芯FN4、FN6、FN8的过滤效率均大于任何层数的未处理滤芯F4、F6、F8，4 层的改性滤芯FN4 在所有滤芯中有最低的稳态压降，且其效率高于未处理滤芯F4、F6、F8。改性滤芯可以在较少的层数下，保持比多层的未处理滤芯更高的过滤效率以及更低的压降，优化滤芯综合过滤性能，在图14中可以得到印证，改性滤芯FN4拥有最高的品质因子。因此，改性处理能够提高滤芯的过滤性能，尤其在滤芯层数少的时候优势更为明显。

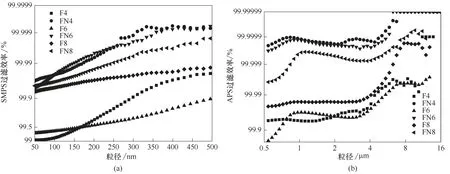
图13 滤芯过滤效率对比Fig.13 Comparison of filtration efficiency for filters

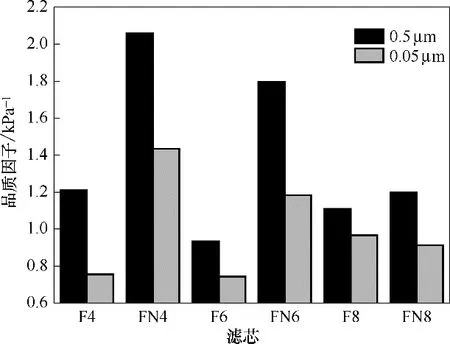
图14 滤芯品质因子对比Fig.14 Comparison of quality factor for filters

3 结 论

（1）提高聚结元件过滤效率的同时，一般伴随着阻力的升高，本文提出一种改性方法，可以使滤材过滤效率提高10%的同时，稳态压降降低约30%。滤材效率的提高由扩散、惯性分离作用的增强和二次夹带的减少导致；滤材压降的降低主要由滤材毛细作用力的改变而导致。

（2）纤维表面能通过影响液滴与纤维的接触形态，进而影响滤材过滤性能。对于结构参数相同的疏油滤材，其稳态压降和过滤效率均随表面能的减小而升高。

（3）经过改性后的聚结滤芯具有低阻高效的优势，尤其在滤芯层数少的时候优势更为明显，其品质因子最大可提高92%。