铁路技术规章制修订协同机制研究

韩富强，贾永刚，谢 祥，保鲁昆

（1.北京交通大学 经济管理学院，北京 100044；2.中国铁道科学研究院集团有限公司 运输及经济研究所，北京 100081；3.中国国家铁路集团有限公司 川藏办，北京 100844)

0 引言

铁路技术规章的制修订严格遵循一定的管理流程，现行《中国铁路运输技术规章管理办法》对基本技术规章和专业技术规章制修订职责进行了明确规定。基本技术规章采用中国国家铁路集团有限公司(以下简称“国铁集团”)的归口管理部门负责组织协调，相关专业部门参与的协作模式，该模式可界定为“无专业部门牵头的技术规章制修订模式”；单个专业内部的技术规章由各专业自行负责制修订，而跨专业的技术规章则采用主办专业部门负责组织协调，其他相关专业部门参与的协作模式[1-2]，该模式可视为“有专业部门牵头的技术规章制修订模式”。在涉及多专业技术规章制修订过程中，参与的各专业部门通过不断协调、沟通与博弈，协同完成相关技术规章的制修订。这些专业部门间的协同合作是以形成共同收益，且自身利益得到充分保障为基础。然而，在技术规章制修订的现实情境中，技术规章的整体收益与各专业部门追求自身利益最大化通常无法实现完美结合，虽然技术规章整体收益有助于提升各专业部门的自身利益，但各专业部门追求自身利益最大化的行为策略，往往会与技术规章整体收益形成冲突，这种利益博弈就造成了技术规章制修订过程中存在专业部门合作困难，最终规章无法及时制定发布或者未到达预期制定目标的困境。

博弈论是一门研究策略性决策行为的社会科学分支，为解释多方参与竞合的内在动机提供了分析工具[3-6]。唐彬等[7]针对铁路局集团公司内部不同部门的利益取向构建三方动态博弈模型，提出大力发展铁路重载运输等发展建议。本文将以经典博弈论中的“囚徒困境”博弈模型[8-9]为基础，使用动态博弈模型[10]对铁路技术规章制修订进行系统建模，并使用逆向归纳法对模型进行求解，根据求解结果提出铁路技术规章协同机制行动策略。

1 基于“囚徒困境”模型的技术规章制修订协同行动机制

1.1 技术规章制修订的“囚徒困境”模型

在铁路技术规章制修订的过程中，模型假设如下。

（1）专业部门A和专业部门B均有“合作”和“不合作”2种选择，R是双方在技术规章制修订过程中均合作时各专业部门得到的收益，T是双方均不合作时各专业部门得到的收益。

（2）当某一专业部门选择“合作”策略，而另一专业部门选择“不合作”策略时，选择“合作”策略的专业部门的收益由P表示，选择“不合作”策略的专业部门的收益由Q表示。在此情况下，选择“合作”策略的专业部门由于受到选择“不合作”策略的专业部门的影响，成本明显提高，其收益P＜R。另一方面，选择“不合作”策略的专业部门，不仅可以获得由技术规章制修订后带来的收益，而且减少了成本的投入，其可以获得高于“合作”策略的收益Q。因此，Q＞R＞T＞P。技术规章制修订囚徒困境收益矩阵如表1所示。

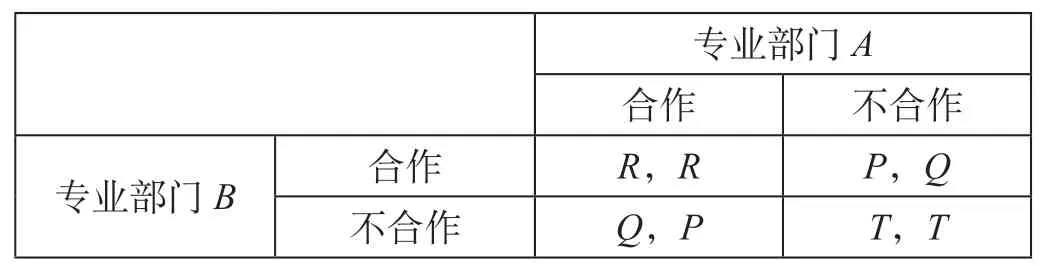
表1 技术规章制修订囚徒困境收益矩阵Tab.1 Prisoners’ Dilemma return matrix for railway technical regulations Formulation

在技术规章制修订博弈模型中，虽然专业部门A、B同时选择“合作”策略获得(R，R)收益大于同时选择“不合作”策略，但由于专业部门A、B之间是作为独立的利益主体存在，具有追求自身利益最大化的动机。专业部门A、B受个体利益的驱使，如果双方在一开始达成合作，但由于Q＞R，因此，其中专业部门A会选择“不合作”策略，专业部门B在预期专业部门A选择“不合作”策略的情况下，其最优策略也是选择“不合作”策略，从而得到该博弈的纳什均衡。

从“囚徒困境”模型的分析中可总结出技术规章制修订过程中专业部门间合作困境产生机理：专业部门个体利益与技术规章整体利益并不协调，缺乏对于合作行为利益的保障是专业部门间合作困境产生的主要原因。在不能确定专业部门合作意愿的情况下，主动遵守合作的专业部门的收益受到“不合作”专业部门的影响，其技术规章制修订的各方面成本提高，收益明显降低；而“不合作”的专业部门却能够获得技术规章制修订成本减少带来的收益。因此，各专业部门最终往往会选择“不合作”策略，从而陷入“囚徒困境”中。

1.2 技术规章制修订协同的行动机制

为了提升技术规章制修订管理水平，保证技术规章整体收益最大，必须打破技术规章制修订过程中“囚徒困境”的问题，通过加强对技术规章制修订过程中参与各方的监管，将技术规章制修订的共同利益与专业部门利益相结合，实现对技术规章制修订过程的动态管理。铁路技术规章制修订协调机制的基本原理如图1所示。

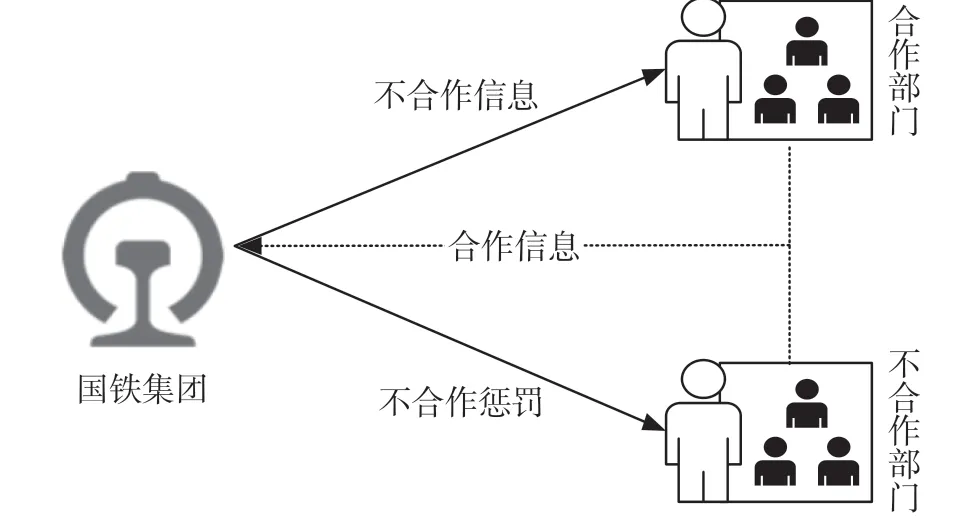
图1 铁路技术规章制修订协同机制的基本原理Fig.1 Basic principles of the coordination mechanism for the formulation of railway technical regulations

从图1可以看出，国铁集团作为技术规章制修订的监管单位，通过不断获取合作专业部门和不合作专业部门间的信息，定位在技术规章制修订过程中的不合作单位。一方面，通过向合作专业部门及时通告不合作信息，使合作专业部门及时部署技术规章制修订计划，减少不合作专业部门带来的损失；另一方面，对不合作专业部门进行不合作惩罚，提高不合作专业部门的成本，实现对技术规章制修订过程中不合作行为的有效治理。

国铁集团加强技术规章制修订监管后，将会改变博弈双方的纳什均衡策略。假设双方合作时各部门所得收益R与双方不合作各部门所得收益T不发生变化；由于国铁集团的严格监管，需要对技术规章制修订过程中一方专业部门选择“合作”策略而另一专业部门选择“不合作”策略时的收益进行调整，在此情境下选择“合作”策略的专业部门的收益由P1表示，由于国铁集团及时通告“不合作”信息，为合作专业部门减少损失，因此P1＞P；选择“不合作”策略的专业部门的收益由Q1表示，由于国铁集团加大对“不合作”专业部门的惩罚力度，因此Q＞Q1；由此，国铁集团严格监管下博弈双方的收益满足R＞Q1＞P1＞T。国铁集团严格监管下博弈双方的收益矩阵如表2所示。

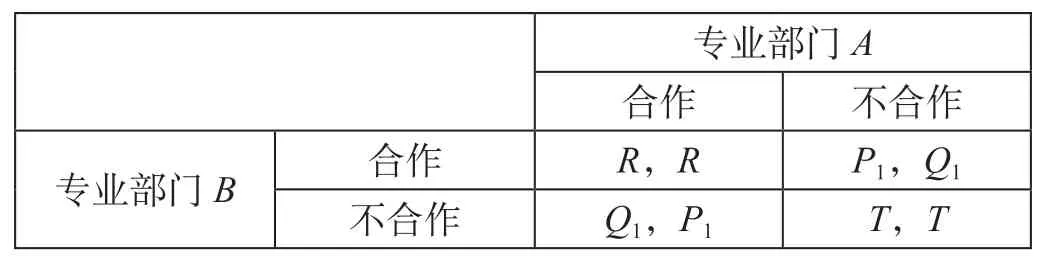
表2 国铁集团严格监管下技术规章制修订收益矩阵Tab,2 Return matrix for railway technical regulations formulated under strict supervision of China Railway

国铁集团严格监管下专业部门之间博弈的纳什均衡是(合作，合作)。当专业部门A选择策略“合作”时，专业部门B选择“合作”的策略时收益为R，选择“不合作”策略时的收益为Q1，由于R＞Q1，因此专业部门B选择“合作”策略可以获得比选择“不合作”策略更高的收益；当专业部门A选择“不合作”策略时，专业部门B选择“合作”的策略时收益为P1，选择“不合作”策略时的收益为T，由于P1＞T，因此专业部门B选择“合作”策略可以获得比选择“不合作”策略更高的收益，“合作”是专业部门B的占优策略。同理，“合作”也是专业部门A的占优策略。由此，(合作，合作)是专业部门A与专业部门B博弈的纳什均衡策略。因此，国铁集团应建立高效的监督约束机制，在制修订技术规章合作过程中，通过明确规定各专业部门的权利和义务，并及时向合作部门通报合作信息，对不合作企业进行惩罚，以此来保障技术规章制修订过程中各专业部门的合作水平。

为了使研究成果更具有普遍性，更加适应技术规章制修订的实际情况，将模型进行扩展，研究专业部门间重复合作、以及顺序合作过程中的博弈问题，使用重复博弈和动态博弈方法对该模型做进一步分析。

2 无专业部门牵头的技术规章制修订行动博弈

在技术规章制修订的过程中需要不同专业部门间的多次合作，因此，以表2国铁集团严格监管下技术规章制修订收益矩阵为基础，系统分析铁路技术规章制修订协同机制在重复博弈中的应用，引入δ(0 ＜δ＜ 1)为无限次重复博弈中的贴现因子(假设各专业部门贴现因子相同)，贴现因子δ反映了专业部门对未来收益的看法，贴现因子δ越大，未来的收益越为重要。对无专业部门牵头的技术规章制修订问题，专业部门在无限次重复博弈中获得的收益是所有阶段进行博弈所获得收益的贴现值之和。专业部门不同的初始策略选择影响技术规章制修订过程中合作均衡及其稳定性，根据专业部门合作策略的不同，分为针锋相对战略和冷酷战略2种策略进行分析。

2.1 针锋相对战略下的重复博弈

在针锋相对战略，技术规章制修订过程中，参与专业部门一开始即选择“合作”策略，接下来在t阶段的时候选择对手在t-1阶段的策略选择。在针锋相对战略中，“合作”策略均为参与专业部门的初始策略，专业部门之间的合作会持续保持下去，每个阶段的收益都是R，双方通过参与技术规章制修订各自获得的收益总额(用π表示)相等，收益总额计算如下所示。

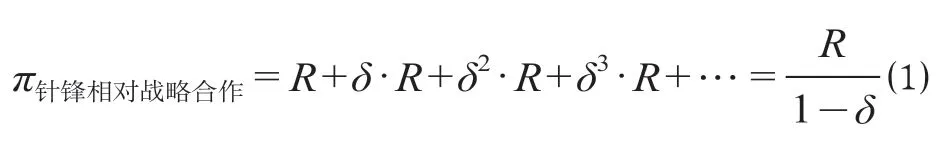
技术规章制修订过程中，如果某一参与专业部门，在此假定为专业部门A，专业部门A出于个体利益的考虑，在博弈的初始阶段，率先选择“不合作”，在针锋相对战略下，在接下来的t-1阶段的博弈中总会发生一方专业部门选择“合作”策略，另一方参与部门选择“不合作”策略的现象。在此情况下，专业部门A获得的收益如下所示。

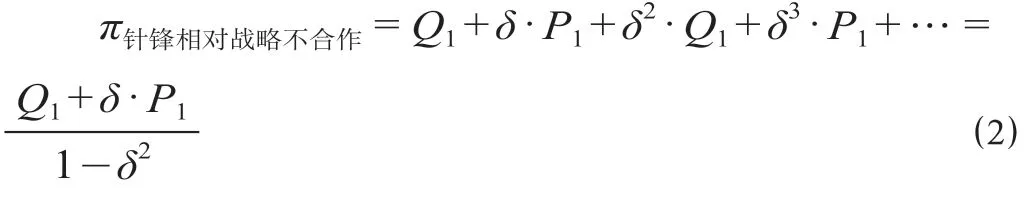
当参与专业部门都选择“合作”策略所获得的收益大于选择“不合作”策略时获得的收益时π针锋相对战略合作≥π针锋相对战略不合作，即，专业部门A会选择“合作”策略，故专业部门之间的合作关系可以长期延续下去，对不等式进行整理可得

因此，当参与技术规章制修订的专业部门在无限次重复博弈中采取针锋相对战略时，只要贴现因子δ能够满足公式3，专业部门参与技术规章制修订所期待获得的长期收益比短期不合作所获得的收益大，最终专业部门间会选择合作、相互协作的道路，有效提升技术规章制修订的质量和效率。

2.2 冷酷战略下的重复博弈

在冷酷战略中，技术规章制修订过程中如果所有专业部门都选择“合作”策略，那么博弈双方的合作关系会一直持续下去。每个阶段的收益都是R，双方分别获得的收益总额(用π表示)相等，计算公式如下。

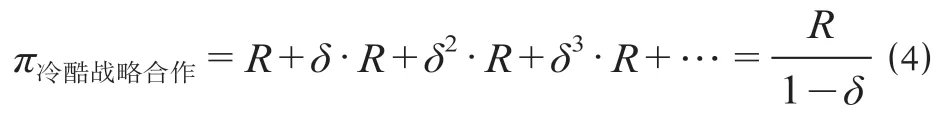
技术规章制修订过程中，当双方的博弈进展到某一个阶段的时候，如果专业部门A采取“不合作”策略，从而引发专业部门B永远不再选择“合作”策略。由此，专业部门A只能继续选择“不合作”策略，此后专业部门A在博弈的每个阶段获得收益T。在此情境下，专业部门A获得的收益如下所示。

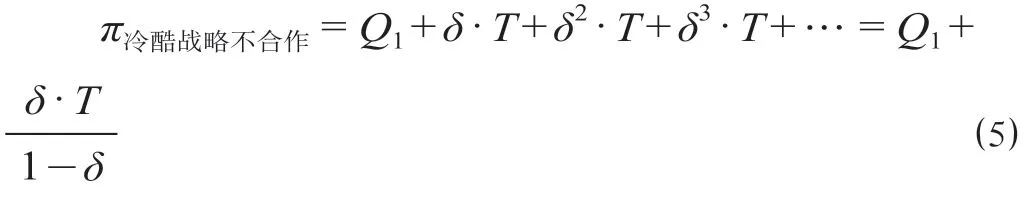
当π冷酷战略合作≥π冷酷战略不合作时，即，对不等式进行整理可得

当参与技术规章制修订的专业部门在无限次重复博弈中采取冷酷战略时，只要贴现因子δ能够满足公式6，冷酷战略无疑是无限次重复博弈的子博弈精炼纳什均衡，结果就是每一阶段参与专业部门都选择合作策略，切实提升技术规章制修订的质量和效率。

3 专业部门牵头的技术规章制修订行动博弈

3.1 专业部门牵头的技术规章制修订过程

有专业部门牵头的技术规章制修订过程中，牵头专业部门根据技术规章制修订的需求，按顺序不断与配合部门进行合作。在动态博弈过程中，参与部门的行动有了先后顺序，先行动部门也能在进行策略选择时会考虑后行动部门的反应，后行动部门在行动之前可以了解到先行动部门之前的行动。本文使用动态博弈法，系统分析完全信息与不完全信息下有专业部门牵头的技术规章制修订问题。

为了便于动态博弈分析，本文假设在有专业部门牵头的技术规章制修订动态博弈过程中有一个牵头专业部门A，以及2个配合专业部门B和C。博弈主体行动顺序为牵头专业部门A-＞配合专业部门B-＞配合专业部门C。根据表2国铁集团严格监管下技术规章制修订收益矩阵进行调整，博弈参与方的收益为：

3个专业部门选择“合作”策略，没有专业部门选择“不合作”策略时，3个专业部门均获得收益R1。2个专业部门选择“合作”策略，一个专业部门选择“不合作”策略时，“合作”专业部门获得收益R2，“不合作”专业部门获得收益T1。一个专业部门选择“合作”策略，2个专业部门选择“不合作”策略时，“合作”专业部门获得收益R3，“不合作”专业部门获得收益T2。没有专业部门选择“合作”策略，3个专业部门选择“不合作”策略时，“不合作”专业部门获得收益T3。通过引入技术规章制修订协调机制，对“不合作”策略专业部门加大惩罚，对“合作”策略专业部门及时通报“不合作”部门信息，保障积极参与技术规章制修订企业的合理收益，据此推导出收益的大小关系如下所示。

同时，在技术规章制修订的过程中，专业部门间的协调合作可以获得“1+1＞2”的效果。因此，3个专业部门选择“合作”策略的总收益大于2个专业部门选择“合作”策略的总收益；2个专业部门选择“合作”策略的总收益大于1个专业部门选择“合作”策略的总收益；1个专业部门选择“合作”策略的总收益大于没有专业部门选择“合作”策略的总收益。

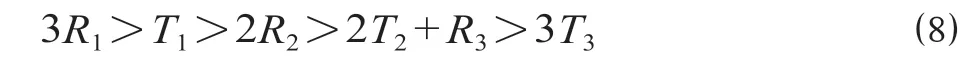
3.2 完全信息下的动态博弈

采用完全信息动态博弈，将由有专业部门牵头的技术规章制修订简化为完美信息动态博弈(每1个信息集都是单结的)。对相关参与部门动态博弈过程分析如下，技术规章制修订过程博弈涉及牵头专业部门A、配合专业部门B、配合专业部门C3方利益主体。其中，第1个数字表示牵头专业部门A所获得的收益，第2个数字表示配合专业部门B所获得的收益，第3个数字表示配合专业部门C所获得的收益。采用博弈树模型进行分析。完全信息下技术指定三方动态博弈树如图2所示。

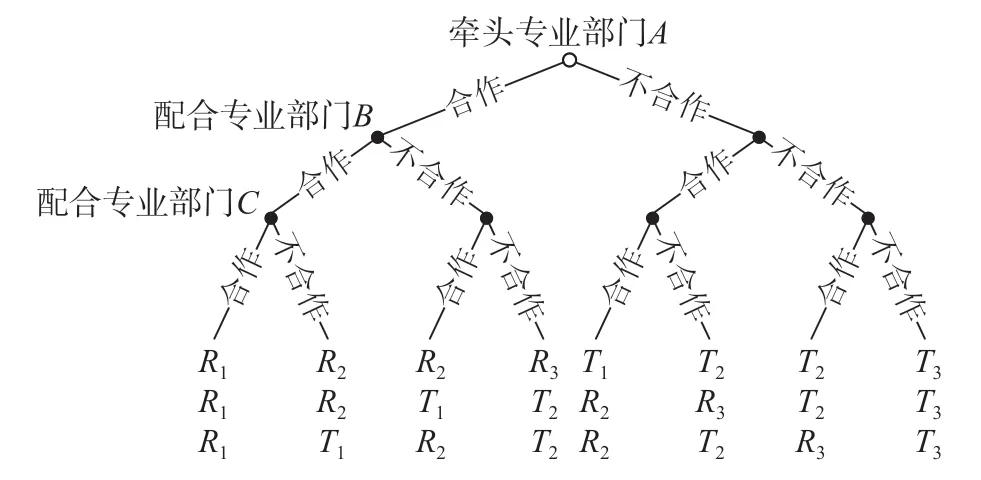
图2 完全信息下技术规章制修订三方动态博弈树Fig.2 Three-party dynamic game tree for railway technical regulation formulation with complete information

确定各策略组合的收益后，由于假设的博弈顺序是牵头专业部门A-＞配合专业部门B-＞配合专业部门C，因此采用逆向归纳法求解时，求解顺序为配合专业部门C-＞配合专业部门B-＞牵头专业部门A。根据公式 ⑺ 和公式 ⑻ 中收益的大小关系，对该博弈模型进行分析，配合专业部门C最后行动，根据所选择策略收益大小的不同，其最优行动策略是{合作，合作，合作，合作}；根据对配合专业部门C行动策略的预测，配合专业部门B的行动策略是{合作，合作}；根据对配合专业部门B行动策略的预测，牵头专业部门A的行动策略是{合作}。最终，用逆向归纳法得到得精炼均衡是3个专业部门均选择“合作”策略。

3.3 完全但不完美信息下的动态博弈

在技术规章制修订部门间博弈过程中，可能受到干扰而无法判断之前的参与部门采取了什么策略，就构成了完全但不完美信息动态博弈。假设配合专业部门C能够观测到牵头专业部门A的策略选择，但无法观测到配合专业部门B的策略选择，博弈三方的收益采用博弈树模型表示。由于配合专业部门B和配合专业部门C均存在占优策略，因此，在确定各策略组合的收益后，采用逆向归纳法求解动态博弈均衡解。

根据公式 ⑺ 和公式 ⑻ 中收益的大小关系，当牵头专业部门A选择“合作”策略时，配合专业部门B选择“合作”策略的情况下，配合专业部门C会选择“合作”策略。当配合专业部门B选择“合作”策略时，配合专业部门C会选择“合作”策略。因此，“合作”策略是配合专业部门C的占优战略。同理“合作”策略也是配合专业部门B的占优战略，故纳什均衡是配合专业部门2者都选择“合作”策略。此时，可以用占优策略替代配合专业部门C和配合专业部门B的策略，然后使用逆向归纳法推导出纳什均衡。牵头专业部门A选择“合作”策略时的收益是R1，选择“不合作”策略时的收益是T1，因此牵头专业部门A会选择“合作”策略。最终纳什均衡为3个参与主体均选择“合作”策略。

3.4 技术规章制修订的行动协同策略

通过博弈论模型对技术规章制修订过程中参与主体间的博弈行为进行分析，说明利益是技术规章制修订过程中专业部门间博弈的出发点，也就是对利益的追逐驱动专业部门选择“合作”或“不合作”策略。通过引入“协调机制”，降低专业部门选择“不合作”策略的收益，提高专业部门选择“合作”策略的收益，帮助技术规章制修订中各参与专业部门走出“囚徒困境”。根据调研，铁路局集团公司《普速铁路行车组织规则》《高速铁路行车组织细则》(以下简称“《行规》”“《行细》”)的制修订过程普遍存在“囚徒困境”现象。主要表现在专业部门出于自身利益考虑，对自身有利的内容往往写的较为清楚，对自身不利的内容，往往不写或写的比较模糊；制修订工作过分依赖技术规章归口管理部门，参与编制工作的主动性不高，属于本专业的内容也依赖归口部门来进行制修订，弱化了专业部门在技术规章制修订中的作用；过分追求部门利益而忽视整体利益，特别是涉及2个专业结合部的事项，不论是由哪个专业部门负责，经常出现无原则的抵制，而不顾及铁路局集团公司整体利益。国铁集团对《行规》《行细》范化编制工作进行协同和博弈分析，基于分析结果，国铁集团制定发布了《〈行规〉〈行细〉编制规则》，明确专业部门在《行规》《行细》制修订中的职责，促进各专业协同配合，实现了《行规》《行细》管理的规范化。具体策略如下。

（1）给专业部门赋权，明确每一条款的编写组织部门和参与编写部门，赋予专业部门职责，调动专业部门合作的积极性。同时赋予牵头专业部门对“不合作”专业部门的协调权，在国铁集团进行惩罚之前，由牵头专业部门先对配合专业部门的收益进行协调，一方面减少国铁集团对《行规》《行细》制修订进行监控的工作量，提高监管效率；另一方面，有利于促进牵头专业部门与配合专业部门形成和谐的合作关系，提高《行规》《行细》制修订的效率。

（2）强化技术规章信息传递，通过引入意见征求、集中研讨等程序，及时将各专业不合作信息传递给相关专业部门，相关专业部门从而能够及时做出反馈和调整，确保《行规》《行细》具体条款的规定达到预期目标要求。

（3）强化技术规章监管，在铁路局集团公司《行规》《行细》制修订过程中，引入专家审查、技术委员会审议等程序，加大对“不合作”专业部门的处罚力度，为确保铁路局集团公司《行规》《行细》整体利益最大化提供了保证。

4 结束语

系统分析了技术规章制修订过程中协同的动力机制，通过构建博弈论模型，解释技术规章制修订中的“不合作”窘境，将“协同机制”具体应用于技术规章制修订的实际情况。针对无专业部门牵头和有专业部门牵头2种情况，分别构建无限次重复博弈模型和动态博弈模型，分析提出技术规章制修订过程中协同机制行动策略，并以铁路局集团公司《行规》《行细》范化编制工作为例分析了应用效果，为提升技术规章制修订管理水平，促进铁路技术规章制修订整体利益最大化提供理论支撑。