针对发车延迟的列车运行图加线模型构建及实证

王锴楷，何世伟，兰泽康，冯 骁

（北京交通大学 交通运输学院，北京 100044)

0 引言

列车运行图规定了铁路运输生产中列车在区间运行以及在各个车站到发或者通过的具体时刻，是铁路系统组织列车运行的基础。货运班列作为一种固定车次、线路的运输形式，在运行图上表现为到发时刻相对固定的运行线，具有运输效率高、经济效益好的优点。然而，在实际运营过程中，由于集结过程存在一定随机因素，可能会出现在规定的时刻无法完成货物集结，继而影响货物作业、编组作业，最终影响货运班列出发时间的情况。因此，对于因货物集结、场站作业等因素而无法按图定时刻出发的货运班列，可以在其满足发车条件的时间点后，以不影响其他列车正常运行为前提，在列车运行图上铺画一条新的运行线，提高货物送达的时效性。

目前，针对列车运行图已经有很多研究。Tan[1]通过构造事件活动图研究运行图结构，建立运行图加线模型。李建等[2]以各列车在途中停留时间加权值的总和最小化为优化目标，建立直达列车运行线选择的0-1整数规划模型，采用粒子群算法对模型进行优化求解。徐涵等[3]考虑周期结构和灵活接续等约束条件，构建基于灵活接续的列车运行图加线模型，实现列车“周期+非周期”运行图铺画的综合优化。刘敏[4]针对列车与客流协调性问题，建立增开本线列车模型，实现输送能力优化配置。张小炳等[5]以车流在途运输时间最小为优化目标，构建基于货物运到期限的列车运行线选择0-1整数规划模型，采用模拟退火算法求解。周浩然[6]针对铁路系统特定区间的扰动情况，采用混合整数规划模型实现临时待避方案的生成。江峰等[7]构造时空网络将列车运行图铺画转化为路径搜索问题，通过启发式算法求解。郭一唯等[8]以运行时间、追踪时间、停站时间等作为约束条件，建立以运行图均衡性为优化目标的决策模型。

然而，这些研究针对旅客列车运行图调整较多，对于货物列车尤其是货运班列的运行图调整较少，需要针对实际运营中存在的列车发车延迟问题，构建列车运行图加线模型优化原运行图，并通过实际算例进行验证。

1 针对发车延迟的列车运行图加线模型构建

1.1 问题描述

为了直观地描述运行图中的各要素以及要素之间的关联关系，这里采用事件和活动来表示运行图结构。其中，所有列车的到达与出发事件统称为事件，而连接事件的联弧则称为活动，由此可以得到由事件与活动构成的运行图网络G= (E，A)。

E表示事件集合。事件分为2类，一是原图事件Eori，表示原定的运行图，具体标定了原计划中各列车的运行时刻。二是加线事件Eadd，表示调整后的运行图，确定新加的运行线的各个时刻。

A表示活动集合，A= {(i，j) |i，j∈E}，按照类型分为以下4类：①旅行弧。连接同一列车的发车事件与到达事件，其中Aoritrip为原图旅行弧，Aaddtrip为加线旅行弧。②安全间隔弧。Aint为安全间隔弧，连接同一个车站相邻的2个到达事件或者出发事件，表示在同一个车站任何属于不同列车的相邻2个到达事件与出发事件之间必须保持一定时间间隔。③停站弧。Adwell为停站弧，连接同一列车在某站的到达事件与出发事件，表示对于有停车需求的列车在特定的车站进行停车作业的过程。④延迟弧。连接需要进行调整的运行线在起始站的原发车事件和新发车事件，以及在终到站的原到达事件和新到达事件。其中，原发车事件与原到达事件均属于原图事件Eori，新发车事件与新到达事件均属于加线事件Eadd。设定Adeplag为出发延迟弧，Aarrlag为到达延迟弧。

运行图网络示意图如图1所示。

为了使模型更加简洁，提出以下2点基本假设：①除了需要调整的列车运行线，其他运行线不作调整。②对运行线进行调整时，可根据需求在任何车站进行停车作业。

1.2 模型构建

以最小化总延迟时间为目标函数，兼顾总体和局部的运到期限要求，构建针对发车延迟的列车运行图加线模型，具体如下。

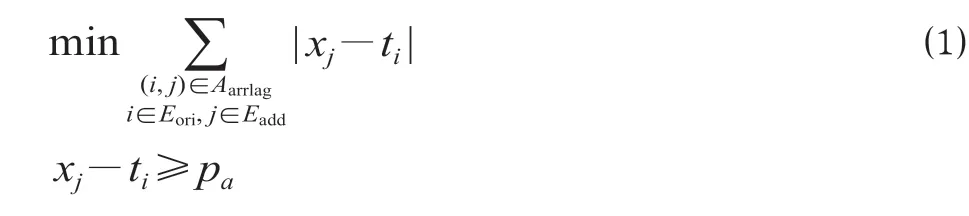
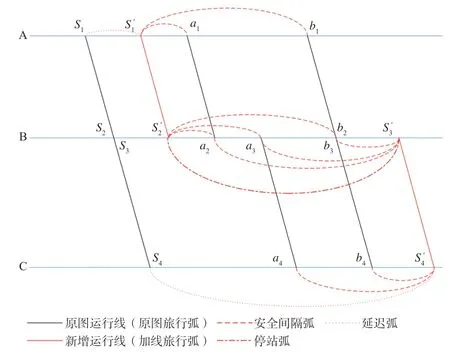
图1 运行图网络示意图Fig.1 Train operation diagram network

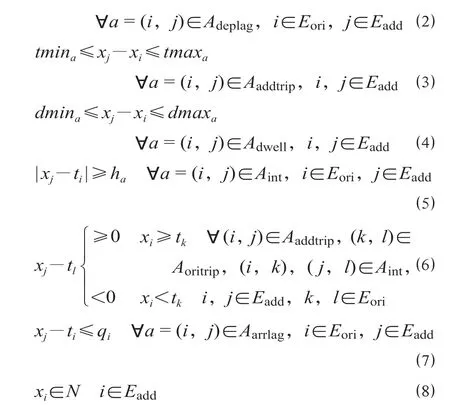
式中：(i，j)表示连接事件的联弧，(i，j)∈A，i是联弧的起点，j是联弧的终点，i，j∈E；dmina和dmaxa分别为停站弧a的最小停站时间和最大停站时间，min；tmina和tmaxa分别为旅行弧a的区间最小旅行时间和区间最大旅行时间，min；ha表示安全间隔弧a的安全间隔时间，min；ti，tk，tl分别表示原图中事件i，k，l发生的时间点，其中i，k，l∈Eori；pa表示需要调整的列车相比原定的发车时间延迟的时间，其中a∈Adeplag，min；qi表示需要调整的列车在原运行图中的终到事件与运到期限之间的冗余值，其中i∈Eori，min；决策变量xi，xj分别表示调整后的列车事件i，j发生的时间点，其中i，j∈Eadd。

公式 ⑴ 为模型的目标函数，表示所有调整后的列车相对于原图最终到达终点站的总延迟时间最小；公式 ⑵ 为列车的出发时间约束，表示需要调整的列车在起点站的出发时间必须晚于列车整备完毕的时间；公式 ⑶ 为列车的旅行时间约束，表示列车在各个区间的运行时间必须处于该区间的最小运行时间与最大运行时间之间，从而保证列车在合理的速度范围内运行；公式 ⑷ 为列车的停站时间约束，表示列车在车站的停站作业时间必须满足作业标准；公式 ⑸ 为列车的安全间隔时间约束，表示对于不同列车在同一个车站的同类型事件必须在时间上保持一定安全间隔，这里考虑到技术站到达场与出发场一般不存在作业冲突，可同时进行到达作业与发车作业，因此对发—到和到—发事件之间的时间间隔不做限制；公式 ⑹ 为列车的区间越行约束，其中(i，j)与(k，l)表示位于同一个区间属于不同列车的2条旅行弧，如果出发事件i的发生时间晚于出发事件k，则i对应的到达事件j的发生时间也晚于与k对应的到达事件l，反之同理，从而保证任何区间都不会发生列车越行现象；公式 ⑺ 为货物运到时限约束，表示每列列车调整后到达终点站的时间都不可超过运到期限，在局部保证运到期限；公式 ⑻ 为决策变量的逻辑约束。

针对发车时间延迟的列车运行图加线模型为整数规划模型，可以采用分支定界法获得精确解。

2 实证分析

（1）线路选择。以中欧班列西通道重要运行线路郑州—阿拉山口为例，涉及沿途8个重要技术站，包括郑州北站(A)、新丰镇站(B)、兰州北站(C)、武威南站(D)、嘉峪关站(E)、哈密东站(F)、乌西站(G)以及阿拉山口(H)。线路示意图如图2所示。

图2 线路示意图Fig.2 Route structure

（2）运行图信息。将列车S1的出发时刻设定为时间原点，记为0，其余时间点以此为原点进行推算，以距离此原点的分钟数表示，单位为min，可以得到原运行图信息如表1所示。运行图示意图如图3所示，共涉及15列列车。

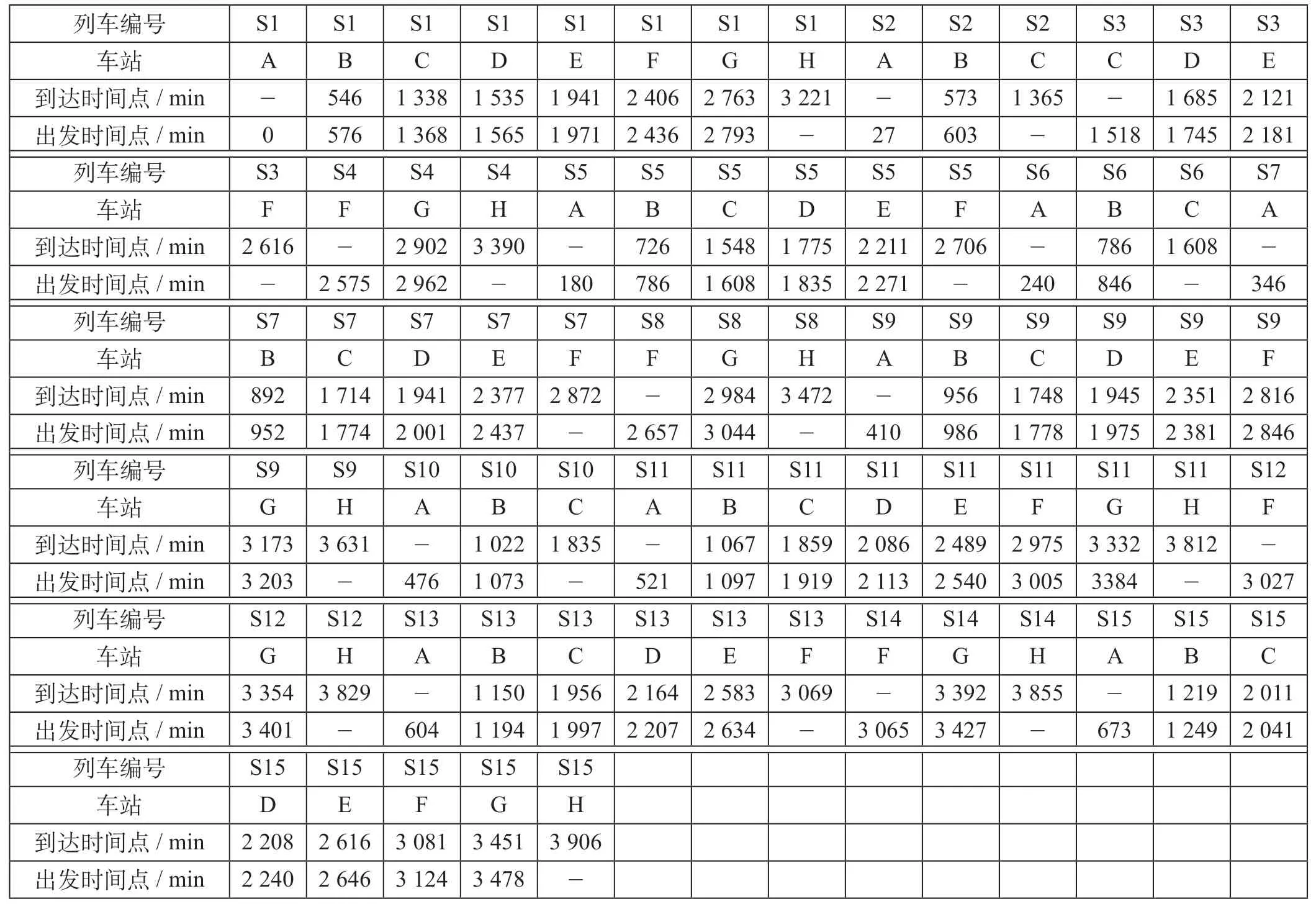
表1 原运行图信息Tab.1 Original train operation diagram information

（3）运行线调整信息。列车S1与S9是服务于A—H的货运班列，由于在货物集结过程中发生时间延误，因此需要延迟从A站出发的时间。运行图调整信息如表2所示。

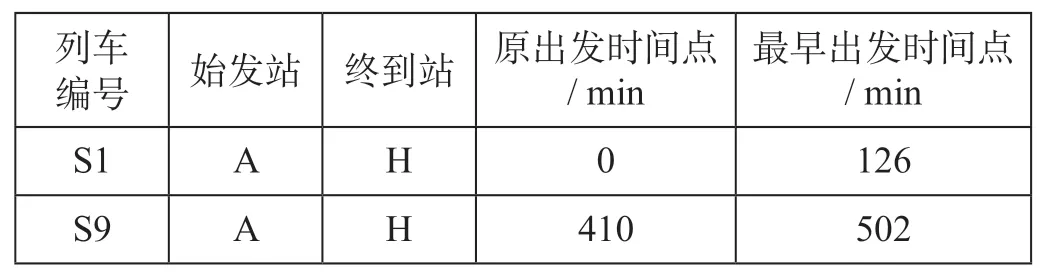
表2 运行图调整信息Tab.2 Train paths alteration information

（4）运行图网络构建。以线路中的车站E(嘉峪关站)为例，新增的列车运行线会在本站产生新的到达事件与出发事件，两者之间建立停站弧。新增的到达事件与原图中属于其他列车运行线的本站到达事件一一建立安全间隔弧，同样地，新增的出发事件与其他列车运行线的本站出发事件一一创建安全间隔弧。特别的，在起点站与终点站，原发车事件和新发车事件以及原到达事件和新到达事件之间分别建立延迟弧。至此，运行图网络构建完成。运行图网络示意图如图4所示，将其简化为网络结构图，网络结构示意图如图5所示。

图4 运行图网络示意图Fig.4 Train operation diagram network

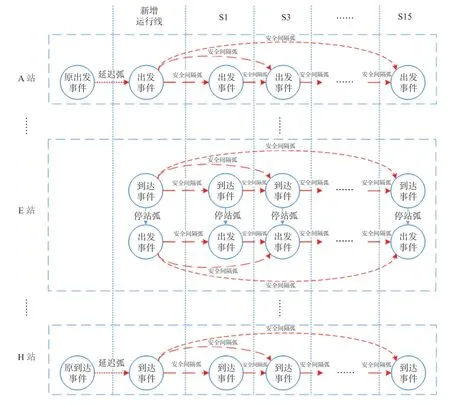
图5 网络结构示意图Fig.5 Network structure

（5）模型参数设定。设定最小停站时间20 min，最大停站时间180 min，区段旅行时间如表3所示。对于从A—H的货运班列，运到期限为4 320 min。

表3 区段旅行时间 minTab.3 Trip time of sections

对针对发车延迟的列车运行图加线模型进行求解，采用以上实例，可以得到调整后列车时刻表如表4所示。相比较于原计划，列车S1的出发时间点调整为146 min，为避免与其他列车冲突，在C站停留144 min，最终在3 521 min到达H站，相比于原运行图推迟300 min；列车S9的出发时间点调整为541 min，最终在3 852 min到达H站，相比于原运行图推迟221 min。根据模型优化的结果，调整后的总延迟时间为521 min，并且2列列车调整后均未超出各自的运到期限。结果表明，针对发车延迟的列车运行图加线模型可快速有效地提供特殊状况下的列车运行图临时调整方案，验证了模型的有效性和可行性。

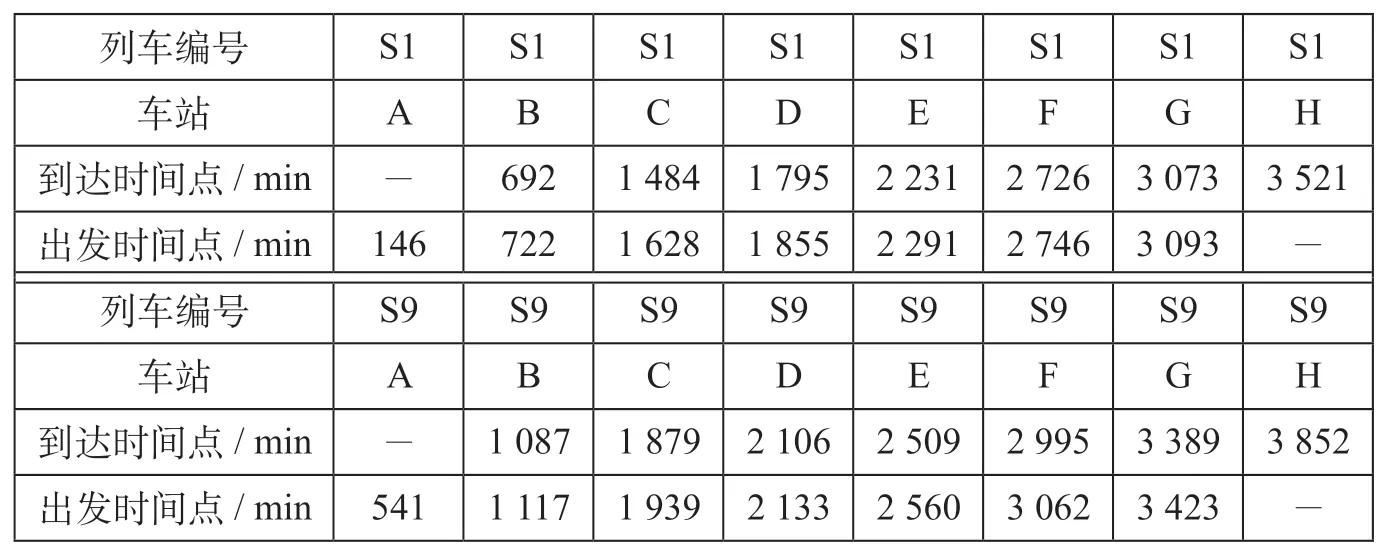
表4 调整后列车时刻表Tab.4 Train paths after adjustment

3 结束语

实际运营存在由于外界因素影响使得货运班列无法按原计划发车的情况，研究基于不影响其他列车正常运行的前提，充分考虑列车的运行特点以及货运的时效性要求，采用加线模型实现列车运行图调整的综合优化。通过实证验算结果表明，该模型能够同时兼顾宏观的调整量最小和微观的时效性最优，在较短时间内生成运行线的调整方案，可以为铁路运营部门提供辅助决策。但是，该模型仅仅针对单一班列考虑，没有考虑列车之间的接续关系，还应进一步考虑对其他货物列车的影响进行综合优化。