不同桥梁结构多尺度建模方法比选①

□□ 张 凡，贾明晓，刘祖军，马 帅 (.华北水利水电大学，河南 郑州 450045； .南阳市污水净化中心，河南 南阳 473000)

引言

随着有限元技术的迅猛发展，工程计算的准确性和效率越来越受到重视[1]。为了满足工程的需要，兼顾计算效率和计算精度的多尺度建模方法逐渐被运用到结构分析中。目前对于多尺度建模方法的研究，要点在于宏观与细观界面处不同单元节点自由度能保持变形协调[2]。因此，本文基于有限元软件ANSYS建立一四跨连续箱梁桥的精细模型和多尺度模型，旨在探究不同的多尺度建模方法在多尺度桥梁中的适用性。

多尺度建模方法是指在同一个计算模型中既包含高效率的宏观单元又包含高精度的精细单元，不同单元在同一个模型中通过一定的方法进行耦合连接，从而使整个结构的计算时间和精度达到平衡[3]。近年来，国内外学者对多尺度建模方法的研究取得了显著成果，为结构多尺度损伤分析提出了许多可行性的模拟方法。周凌宇等[4]通过虚设梁单元法建立了连续组合桥梁腹杆与负弯矩区受力性能研究的多尺度模型。刘亮等[5]通过运用有限元软件ABAQUS中的coupling实现多尺度单元间的自由度耦合，并验证了多尺度模型的精确性。王文博[6]通过双梁模型的有限元解与解析解，说明了MPC和CERIG单元连接的内在机理。曲文辉、李众[7]分别采用四种多尺度建模方法建立了体壳混合单元以及纯实体单元和纯壳单元，对比几种模型在不同工况作用下的应力数据，提出CERIG法最适合于体壳单元的连接。郑吴悰[8]运用四种多尺度连接方法，建立了不同类别的多尺度模型，对比了不同工况作用下静力受力特性和整体模型的动力特性，比选出CERIG法最适合于板桩式路基的多尺度建模方法。卢星辅等[9]通过三种多尺度建模方式建立了三维矿井巷道模型，并对其计算结果进行对比分析，总结出了各方法的优缺点。综上所述，由于不同的多尺度建模方法的界面连接原理不同，应用在不同领域最适用的多尺度建模方法也不同，因此，研究多尺度建模方法在桥结构中的应用是很有必要的。

目前在ANSYS中常用的多尺度建模技术有接触法、应用CERIG和RBE3的表面约束法、约束方程法、刚性杆单元连接法等[10]。为探究不同的多尺度建模方法在多尺度桥梁中的适用性，本文基于有限元软件ANSYS建立以一箱梁桥有限元模型，选择最常见的四种多尺度分析方法，分别利用MPC法、RBE3法、CERIG法、约束方程法连接多尺度模型，对其分析结果与精细模型进行比较，结合实际情况，分析四种方法的不足，比选出最适用于桥梁结构的多尺度建模方法。

1 多尺度界面连接

目前对于多尺度方法的研究，核心问题在于选择一个合适的界面连接方式[11]。如梁单元和实体单元，由于两种单元自由度不同，在进行有限元分析时转角位移无法传递，会出现“刚度矩阵奇异”，因此必须考虑不同尺度单元之间的协调问题[12]。不同尺度单元的界面连接方法有很多，目前在结构多尺度领域最常用的方法有MPC法、RBE3法、CERIG法、约束方程法等。

1.1 MPC多点约束法

MPC多点约束法建立的是多点约束关系，是多节点约束法的一种。以图1梁单元与实体单元的连接为例，其一般计算方程为：

(1)

式中，i——实体单元在交界面上节点的在某方向位移编号；

j——梁单元在交界面上的节点编号；

ui、uj——节点在某方向的位移；

Cj——权重系数；

C0——常数；

L——实体单元节点与梁单元节点的距离，此处L=2。

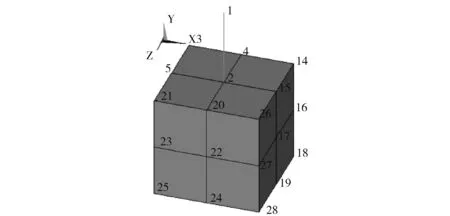
图1 梁—实体多尺度模型

若梁单元在节点2处发生ROTZ转动，连接面上实体单元的节点将产生竖向位移UY，其计算方程为：

UY5=sin(ROTZ2)·L

(2)

-UY9=sin(ROTZ2)·L

(3)

由式(2)和式(3)可以推导出式：

UY5-UY9-2sin(ROTZ2)·L=0

(4)

当发生小转动时，sin(ROTZ2)≈ROTZ2，式(4)可以改写成：

UY5-UY9-2sin(ROTZ2)·L=0

(5)

MPC法的约束方程是由ANSYS系统内部自动生成[8,11]，通过位移方程实现不同尺度单元之间的位移协调，在求解小变形的线弹性问题时，其约束方程可以采用式(5)，直接进行计算；在求解于大变形的弹塑性问题时，结构会发生较大的变形，在进行有限元分析时，MPC法能根据结构在每一步的迭代过程中节点变化的实际位置自动更新约束方程，因此，既能用于结构小变形，线弹性分析又能用于结构大变形，弹塑性分析。

1.2 RBE3表面约束法

RBE3表面约束法是在连接面上创建柔性单元，将梁单元节点受到的力以不同的权重系数分配到实体单元节点上，但是实体单元节点自由度的权重系数分配需要合乎实际结构的受力要求，权重系数的设置可以是系统自动生成，也可以手动设置，本文是根据系统自动生成的。RBE3法的本质是线性约束方程，通过力的重分配实现不同尺度单元之间力的传递，在分析大变形问题时，误差较大。

1.3 CERIG表面约束法

CERIG表面约束法与RBE3法类似，是在连接面上创建刚性单元，不需要考虑自由度的权重系数分配就可以满足平截面假定，但是由于连接面是刚性的，会产生额外的连接面刚度。CERIG法的本质是线性约束方程，通过刚性单元处力的重分配实现不同尺度单元之间力的传递，在分析大变形问题时，误差较大。

1.4 约束方程法

约束方程法是在连接面上手动建立线性约束方程，以便于从一类单元到另一类单元传递载荷，实现连接面的变形协调，约束方程的一般形式是：

(6)

式中，i——方程中项的标号；

DOFi——自由度；

Coefi——权系数。

以图1为例，若梁单元在节点2处发生ROTZ转动，其计算方程为：

ROTZ2=(UY9-UY5)/4

(7)

上式(7)改写为：

UY9-UY5-4ROTZ2=0

(8)

约束方程法的本质是线性约束方程，建立的是位移协调方程，同样不适用于分析大变形问题。

2 多尺度模型构建

2.1 桥梁概况

图2为某在建4 m×20 m 连续梁桥，图3是全桥横截面尺寸图，全桥采用混凝土箱梁桥面系。

图2 桥梁立面布置图(单位：mm)

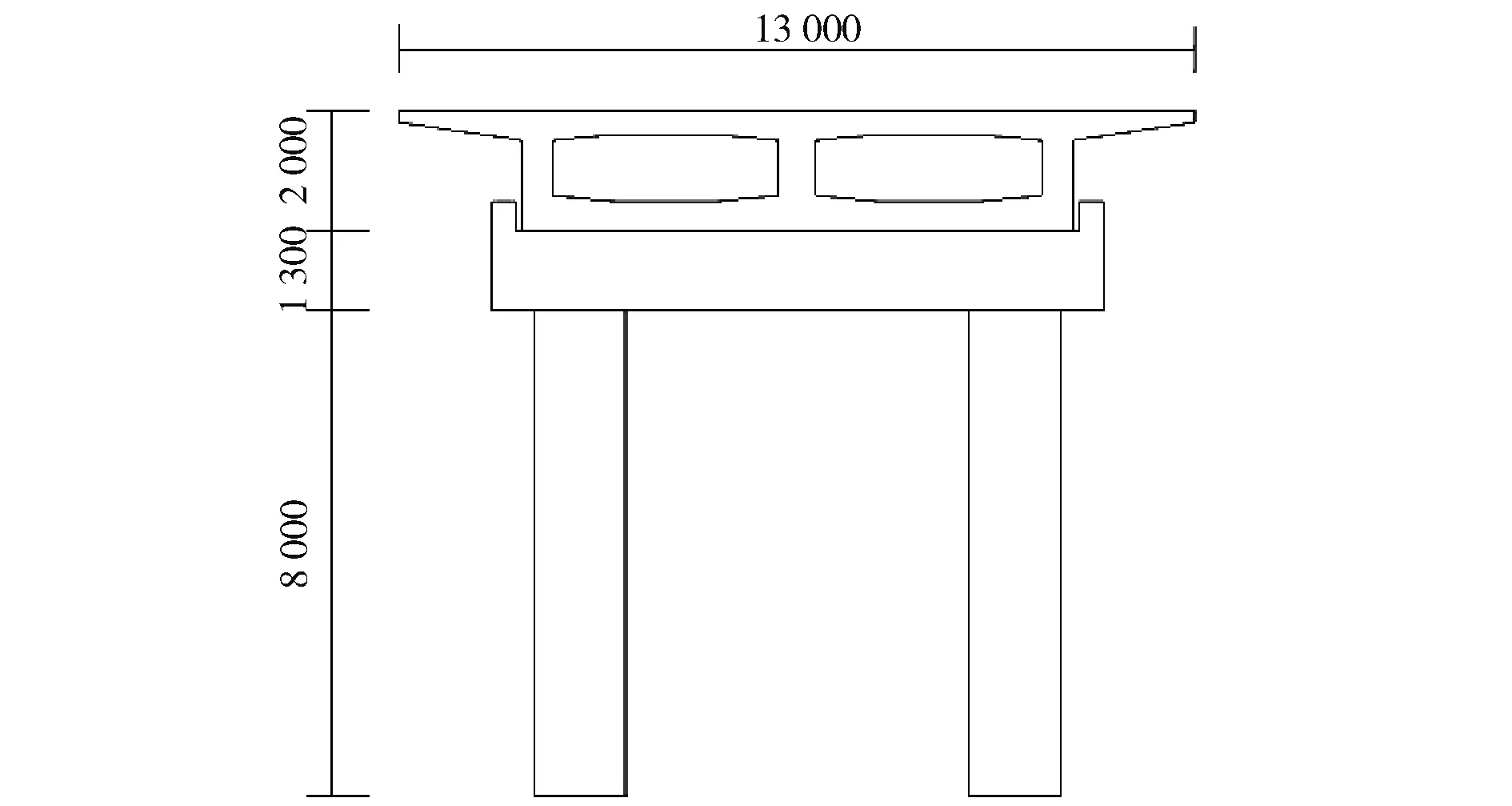
图3 桥梁横截面图(单位：mm)

箱梁上顶面宽为13 m，下底面宽为9 m，梁高为2.0 m，翼缘板外悬为2 m；横梁处梁高为1.3 m，厚度为2 m，横向抗震挡块高度为0.05 m，厚度为0.04 m；桥墩高为8 m，截面为1.5 m×1.5 m；采用单桩基础，桩基础深为25 m，截面为1.5 m×1.5 m；全桥采用C50混凝土、采用HRB400钢筋，钢筋直径为25 mm，全桥采用整体式建模的方式，钢筋等效分配到混凝土中，弹性模量取34 500 MPa，泊松比取0.2。采用有限元程序ANSYS分别构建全桥多尺度模型和精细模型。

2.2 构建多尺度桥梁模型

对桥梁的关键部位采用实体单元solid45进行精细建模，而桥梁的柱和梁的非连接部位采用梁单元beam188进行普通建模，桥墩与梁、墩与桩基之间固定连接，其中精细建模部位主要有三部分。分别是梁与桥墩的连接区域、桥墩部位的塑性铰区域和桩基础，这几个区域受力复杂或者容易破坏，因此进行精细建模。

其中塑性铰区域的确定由国家相关抗震设计规范计算所得[3]：

LP=0.08H+0.022fyds≥0.044fyds

LP=2b/3

(9)

式中，H——桥墩高度；

b——墩的有效计算尺寸；

fy——钢筋屈服强度标准值；

ds——桥墩钢筋直径。

本文的实体单元与梁单元建模的比例就是依据塑性铰理论进行得到，其塑性铰大小为0.816 m。

运用ANSYS建立桥梁的多尺度模型如图4所示。分别用MPC、RBE3、CERIG、建立约束方程四种方法实现多尺度模型中实体单元与梁单元连接界面的协调。

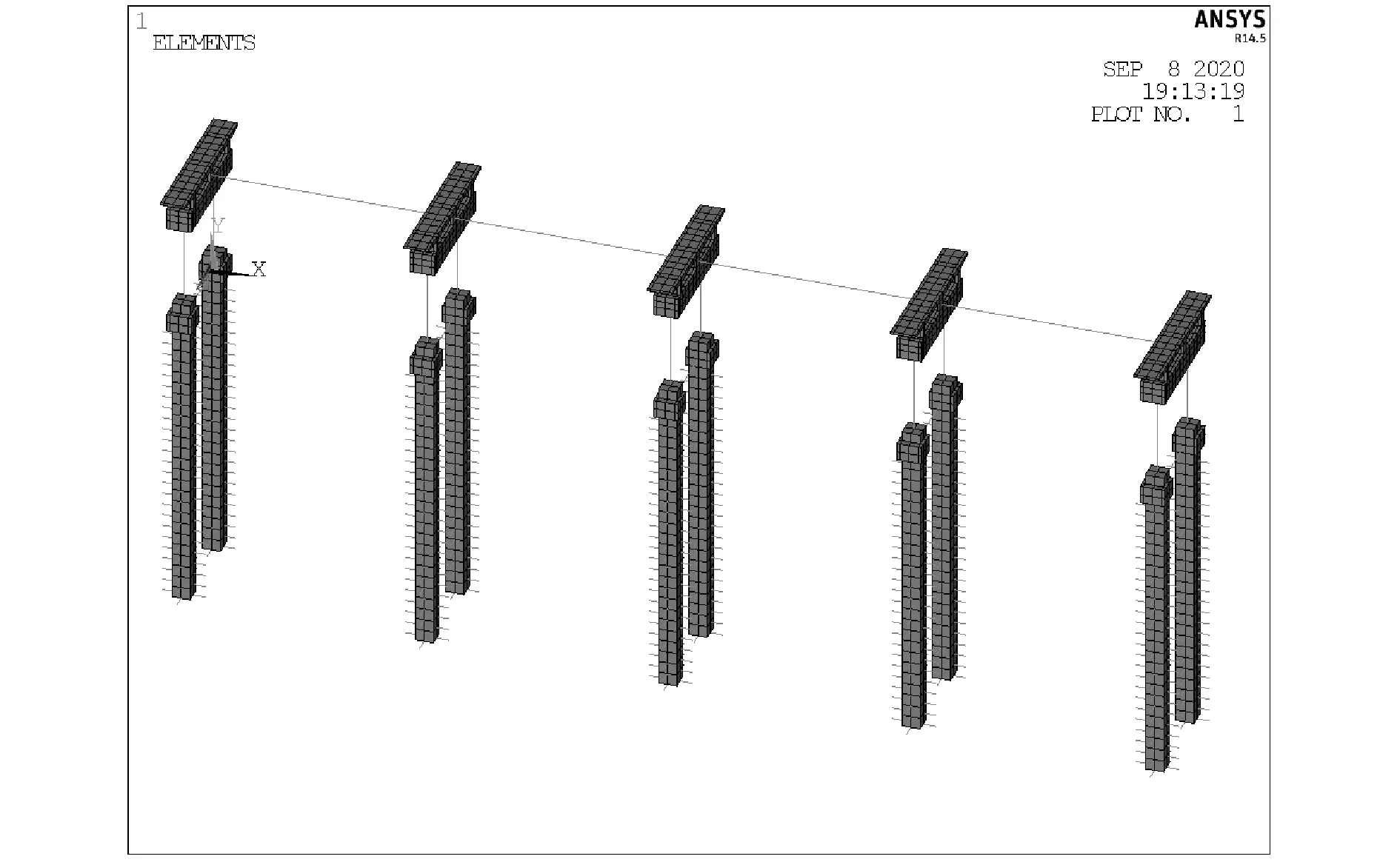
图4 全桥多尺度有限元模型

2.3 桩的模拟

为了使计算结果更为真实，本文对桩基础进行精细建模，并建立土弹簧来模拟桩-土效应，其土弹簧刚度由m法计算所得[13-14]，其土层取值见表1，每个桩建立四组弹簧模拟桩的水平方向受力，并在底部设置竖向固定约束，其中桩基础及土弹簧的模拟如图5所示。

表1 地基土的比例系数

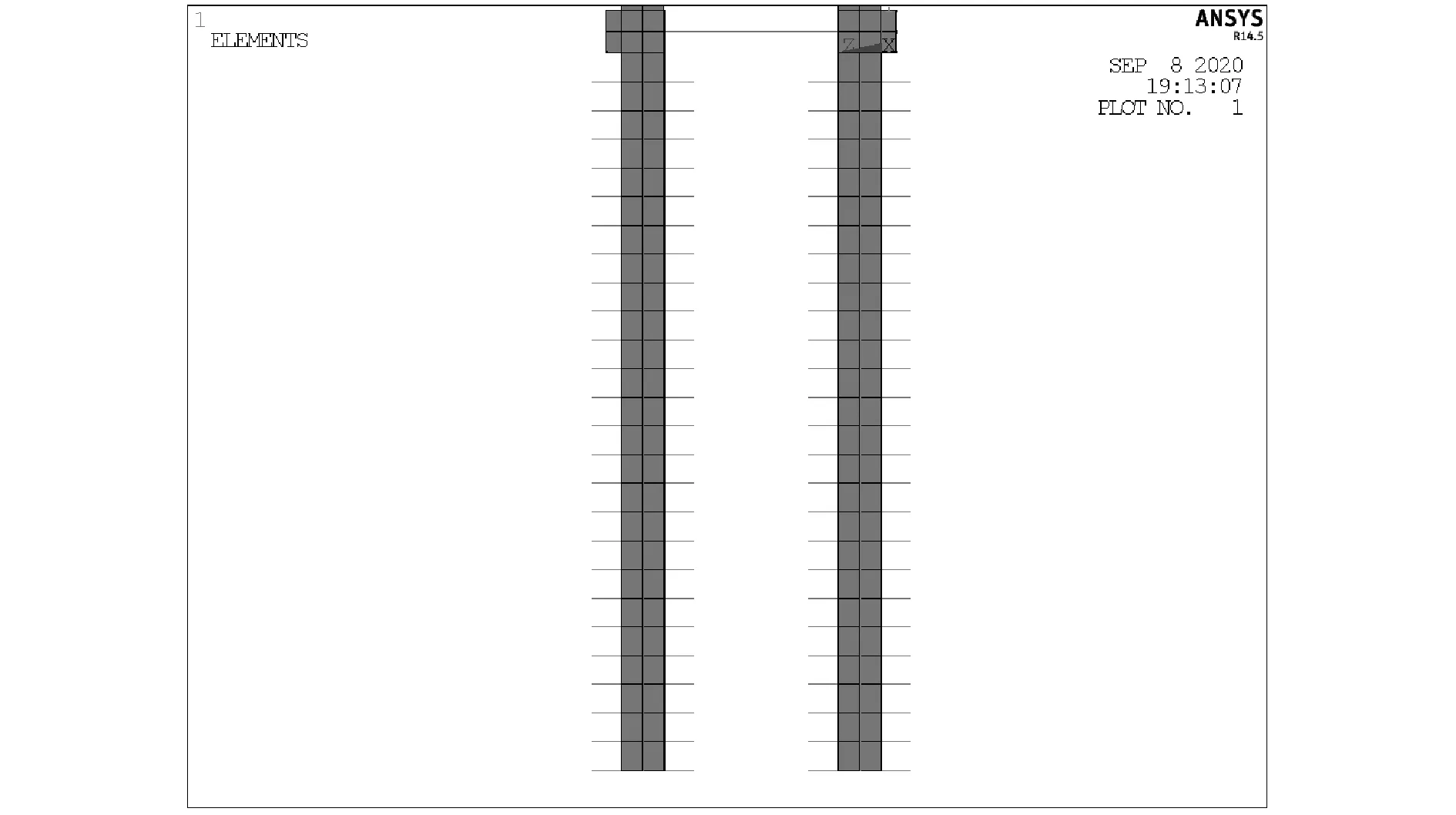
图5 桩基础精细模型

3 结果分析

本文基于多尺度桥梁模型，进行有限元分析，计算得到桥梁结构分别在自重和桥面铺装两种工况下的静力响应和五种模型的动力特性，依次比较四种多尺度连接方法的差异。

3.1 静力响应

基于多尺度桥梁模型，计算自重和桥面铺装两种工况下的力学响应。提取四种多尺度模型与实体模型的最大竖向位移并计算其误差，以此判断各模型的各连接方法对整体刚度的影响。

两种工况作用下的五种计算模型的最大竖向位移见表2。

表2 五种计算模型的最大竖向位移 mm

将四种多尺度模型的最大竖向位移，与实体模型对比，计算出四种模型在两种工况下最大竖向位移的误差见表3。

表3 四种多尺度模型的最大竖向位移误差

由表2和表3可以发现，不同界面连接方法对整体结构刚度的影响差异较大，其中MPC法和CERIG法的误差明显小于其他三种方法，RBE3法和约束方程法误差较大大。

为验证上述结论的准确性，提取桥梁顺桥向多个梁截面最大von_Mises应力进行对比，两种工况作用下的五种计算模型顺桥向多个梁截面最大von_Mises值见表4。

表4 五种计算模型梁截面的最大von_Mises MPa

根据四种多尺度模型梁截面最大von_Mises应力与实体模型对比，计算出四种模型在两种工况下梁截面最大von_Mises应力误差见表5。

表5 四种多尺度模型梁截面的最大von_Mise误差

由表5发现，CERIG法和MPC法的误差较小，明显优于其他方法，RBE3法和约束方程法误差最大。

为了更直观地了解连接面的模拟效果，提取自重工况下第四根横梁与第四根箱梁的连接面的von_Mises应力。

由图6～图10连接面的von_Mises应力云图对比发现，MPC法和CERIG法的有限元计算结果与实体模型最为接近，连接效果最好；RBE3法连接面是柔性，由于其权重系数的分配不合理，在翼缘部位出现应力集中的现象，因此，导致计算结果出现较大的误差；约束方程法存在应力集中问题，导致有限元计算结果误差最大，这也是提取最大竖向位移和最大von_Mises误差很大的原因。

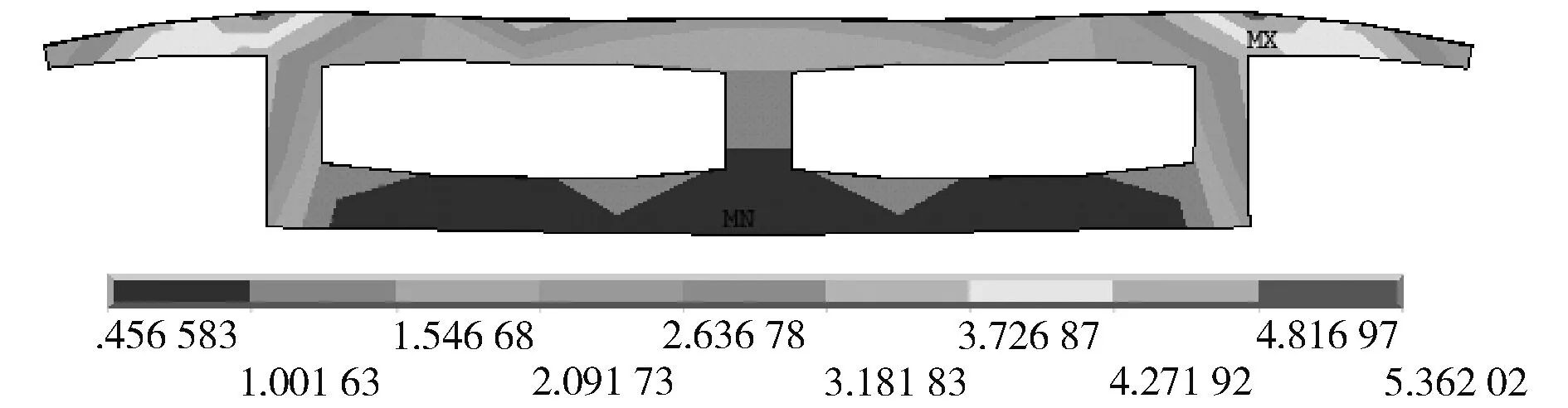
图6 MPC法von_Mises应力云图(单位：MPa)

图7 RBE3法von_Mises应力云图(单位：MPa)

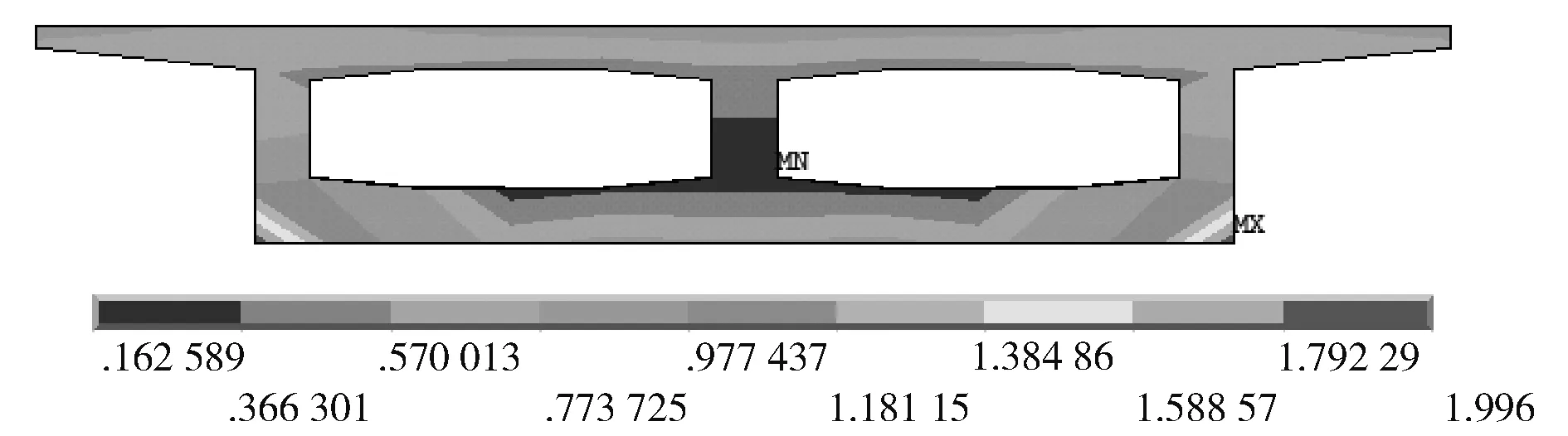
图8 CERIG法von_Mises应力云图(单位：MPa)

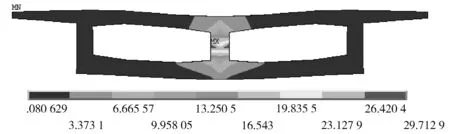
图9 约束方程法von_Mises应力云图(单位：MPa)

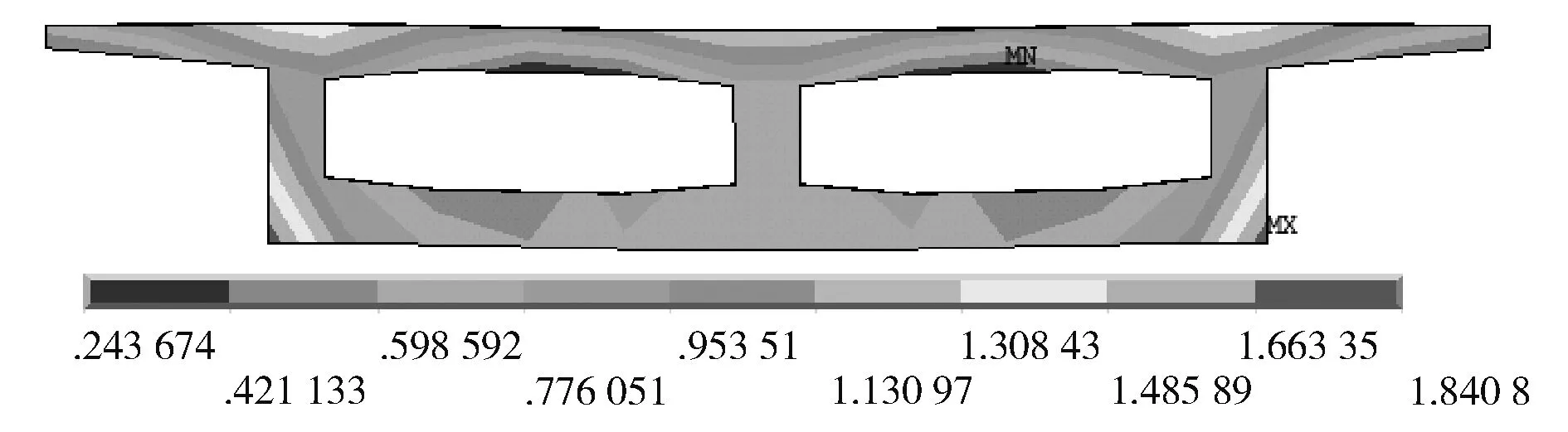
图10 实体模型von_Mises应力云图(单位：MPa)

为探究约束方程法应力集中的原因，提取图9的应力集中区域，如图11所示。

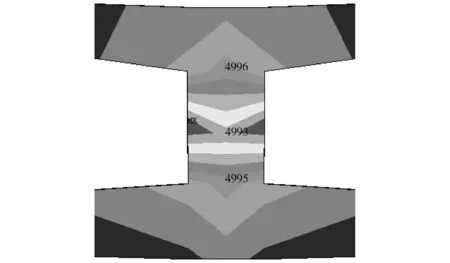
图11 约束方程法von_Mises应力详图

图中从上到下的三个节点编号依次为4996、4993、4995，此处存在约束方程：CE,19,9,0,4996,UX,1,4995,UX,-1,4993,ROTZ,NY(4996)-NY(4995)。当结构受到自重的影响时，会在梁节点4993处产生ROTZ转角位移和Y方向的竖向位移。由于梁单元和实体单元自由度不同，为了实现自由度之间的协调，约束方程将梁节点4993处产生的ROTZ转角位移转换成UX方向水平位移，传递到实体单元的4996节点和4995节点；梁节点Y方向的竖向位移，由于实体单元由UY方向的自由度，则直接传递到实体单元上。本应作用在整个梁截面上的位移，通过约束方程只作用在数个节点，因此会在约束方程连接的节点处产生应力集中的现象。

3.2 自振特性

为研究四种多尺度模震动特性的精确度，本文对四种多尺度模型与精细模型进行模态分析， 并提取前10阶模态阶数进行对比，各模型的自振频率如图12所示。

图12 前10阶自振频率对比(单位：Hz)

为了更直观的观察各阶频率的差异，对各阶频率数值列表显示，见表6。

表6 五种模型前10阶自振频率对照表 Hz

从图12可以看出，对于前四阶自振频率MPC法、RBE3法和CERIG法的结果相差很小；四阶以后，CERIG法自振频率与实体模型几乎一致，MPC法和RBE3法的自振频率略小于实体模型，有较小的误差。手动建立约束方程法的自振频率与实体模型相差较大，对自振频率的模拟效果不够理想。

综合考虑，CERIG法的自震频率与实体模型相比几乎一致，模拟效果也最为合理；其次是MPC法和RBE3法，约束方程法的误差最大。

4 结论

应用有限元软件ANSYS建立实体模型与多尺度模型，分别利用MPC法、RBE3法、CERIG法、建立约束方程法连接多尺度模型，对四种多尺度种模型和实体模型进行静力分析和模态分析，提取计算结果进行对比，得出以下结论。

(1)MPC法是由系统内部创建约束方程，可以很好地实现不同单元之间的位移变形协调，对结构整体位移的影响很小，能够合理的模拟震动特性，且适用于非线性分析，是分析多尺度桥梁最适用的方法。

(2)CERIG法通过刚性单元连接多尺度模型，可以较好的处理不同单元之间的位移变形协调和应力协调，很好地模拟震动特性，但是只适用于线性分析。

(3)RBE3法在应用时需要合理的分配权重系数，由于权重系数分配不够合理，不同单元之间的位移变形协和应力协调均有较大的误差。

(4)约束方程法需要提取相应节点号手动建立约束方程，过程复杂，并且节点连接处出现应力集中现象，模拟效果最差，不便于工程中的使用。