冲击式水轮机喷射机构泥沙磨损特性的数值模拟
葛新峰,孙 洁,李 阳,吴 丹,张 雷,化洪昌
(1.河海大学能源与电气学院,江苏南京 210098;2.江苏理工学院,江苏常州 213001;3.黄河水利科学研究院,河南郑州 450003)
1 研究背景
在冲击式水轮机运行的过程中,水流会携带一定量的泥沙通过机组。对于一些泥沙含量较高的河流而言,喷射机构和转轮都会受到较为严重的磨损,从而造成射流质量下降、功率下降,运行维护成本增加,严重时还可能威胁到机组的安全稳定运行[1]。
对于冲击式水轮机磨损的研究,主要有实验研究和数值计算两种。但是由于实验研究的一些局限性,现在数值计算的方法更加普遍[2]。大多数学者将注意力放在了转轮斗叶内表面磨损的研究上,关注喷射机构磨损的学者较少[3-5];然而,喷射机构的高速射流质量,会直接影响到转轮的动特性,因此,喷射机构也应是磨损研究应该关注的对象。Thapa[6]研究了泥沙对水力机械的冲蚀机理,认为泥沙造成磨损的根本原因是其携带的大量动能,泥沙在流速最高或是水流加速区域的磨损情况最为严重。曹永等[7]经过研究发现,泥沙颗粒对壁面的冲蚀磨损率与颗粒直径呈一定的函数关系。Messa等[2]研究发现,喷嘴和喷针是喷射机构中最容易受到磨损的部件,且喷嘴出口处的磨损更大。曾崇济等[1]对喷射机构自由射流的水固气三相流进行了三维非定常模拟,得到了泥沙直径与随流性、磨损位置的关系。Benzon等[8]和Jo等[9]研究了喷针顶角,喷嘴收缩角对喷射机构效率以及性能的影响。
在数模计算磨损的过程中,计算结果很大程度上依赖于选用的经验或半经验的磨损公式。本文的计算求解是基于Fluent19.2平台的,在Fluent中,有多种磨损模型,如Generic,Finnie,McLaury和Oka模型。其中,Generic模型为广义磨损模型,可以允许用户自己定制磨损模型;Finnie模型最早于1960年提出[10],应用较广,但往往会出现过度预测磨损的情况[11];McLaury模型是一种预测水中砂冲蚀率的模型,该模型主要用于模拟泥浆侵蚀过程中的侵蚀速率[12];Oka模型由Oka等在总结大量实验数据的基础上提出的[13-14],之后也得到一些学者的应用。苏佳慧等[15]对比了4种模型对弯管冲蚀的适用性研究,发现McLaury 模型也会出现过度预测磨损的现象。相比于Oka 模型,Generic 模型留给用户的自由度更大,更便于调整参数。为此,本文磨损模型选用Generic模型。
为探究泥沙颗粒对喷射机构的影响,本文基于Fluent19.2平台,对型号为CJC601-L-45/2X3.5的模型冲击式水轮机单喷嘴进行三维建模,研究对象为泥沙浓度较低、颗粒之间较少发生相互碰撞、且颗粒大小分布较为均匀的含沙水流,采用VOF多相流模型模拟水气两相流,在两相流非定常计算稳定之后,加入离散相,进行离散相模型和磨损模型的计算,研究泥沙的直径、浓度对喷射机构特性的影响。
2 数学模型
2.1 VOF多相流模型VOF模型是一种固定在欧拉网格下的表面跟踪方法,适用于跟踪多种互不相融的流体交界面。在VOF模型中,不同的流体组分共用一套动量方程,计算时记录各流体组分所占有的体积率。本文将水和空气视为连续相,用VOF模型可以很好的跟踪到射流的自由液面。内部的控制方式如式(1)—(7)[16]:
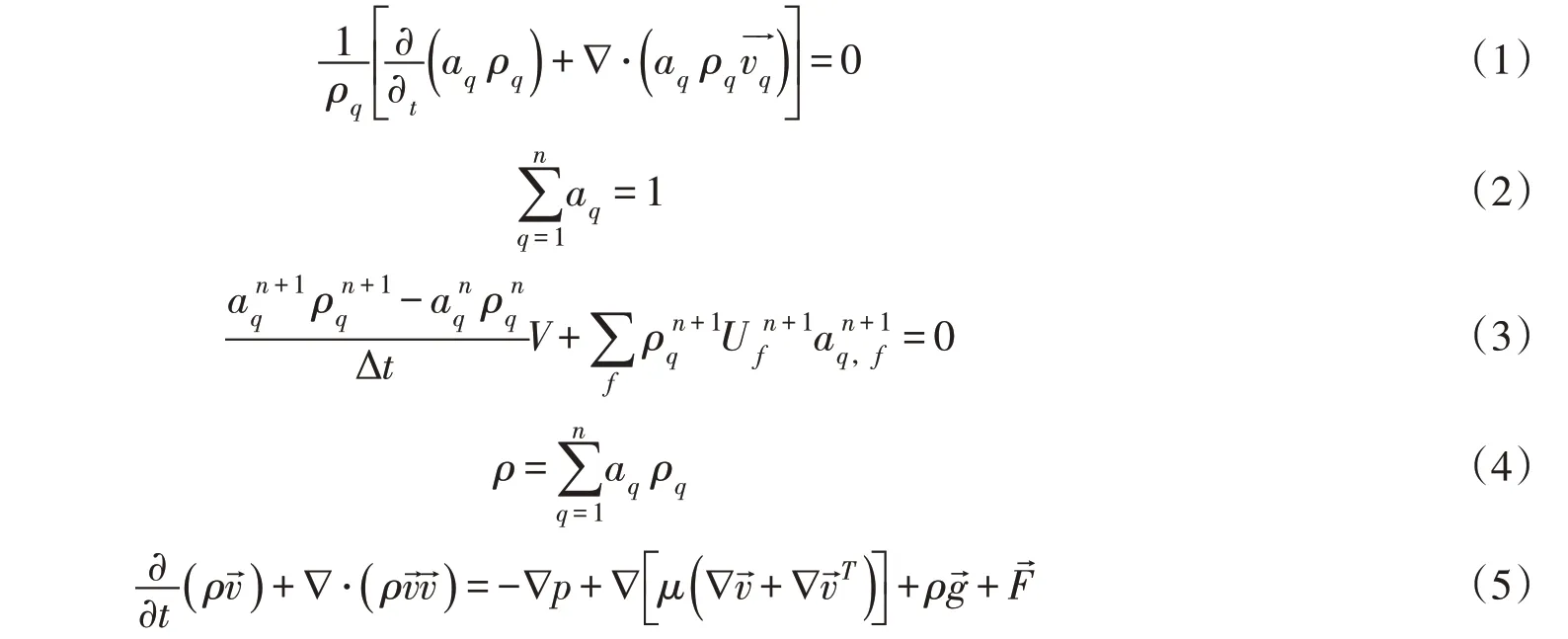
式中:ρq为第q相的物理密度;为第q相的速度;aq为第q相的体积分数;ρ为密度。
2.2 RNG k-ε 模型RNGk-ε模型在标准k-ε模型的基础上做出改进,其计算功能更强。它的湍动能和耗散率方程如下[17]:
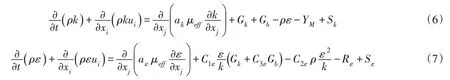
2.3 离散相模型Fluent 中的离散相模型适合于水流中稀疏颗粒的计算,在计算的过程中,忽略粒子间的碰撞,且颗粒体积分数必须低于10%,才能保证计算的准确性,此外,此模型也不适用于无限期悬浮的颗粒流问题。基于以上特点,Fluent中的离散相模型与本文的研究对象是相适应的。在计算过程中,离散相的惯性、曳力、重力都会在拉式公式中考虑到。由于在计算过程中,不考虑泥沙颗粒形状对磨损的影响,将其简化为圆球形,因此曳力模型的公式选择球形颗粒。颗粒的平衡方程在笛卡尔坐标系下的形式为[16]:
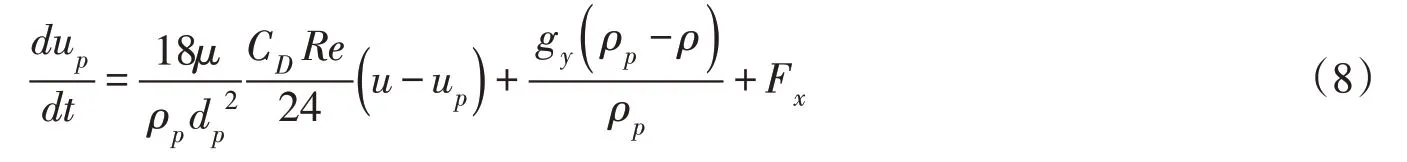
式中:u为流体相速度,m/s;up为颗粒速度,m/s;μ为流体动力黏度,N·s/m2;ρp为颗粒密度,kg/m3;dp为颗粒直径,m;CD为曳力系数,对于球形颗粒可取常数;Re为颗粒雷诺数,定义如下[16]:

颗粒在运动时,其周围流体由于加速作用,会在颗粒上附加作用力,其表达式为[16]:

流场中存在的流体压力梯度引发的附加作用力为[16]:

在计算时,考虑到湍流对颗粒随机性的影响,还应同时开启随机游走模型,使颗粒与流体的离散涡相互作用。此时,流体随机脉动所引起的瞬时速度如下[16]:

2.4 磨损模型含沙水流流过喷射机构时,会对其表面造成切削磨损。应用磨损模型可以监测到泥沙颗粒在所有壁面的磨损和沉积情况。磨损通常与壁面材料、泥沙硬度、水流速度、冲击角度等因素有关[18-19]。本文计算选用Generic磨损模型,粒子在几何壁面上的反射取决于颗粒与固体表面的性质,此次计算选用沙粒对碳钢的表面反射值。冲击角函数采用线性分段函数;壁面恢复系数采用多项式函数;颗粒的直径函数和速度指数函数均设置为常量。这些量的具体设置值都可以在参考文献中找到[20]。冲蚀速率可由下式定义[16]:
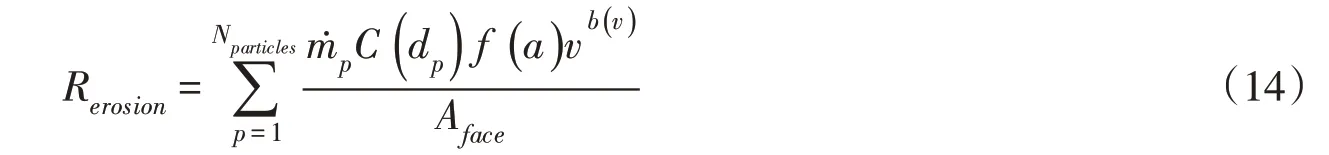
式中:Rerosion为泥沙的冲蚀速率,kg/m2·s,表示壁面材料在单位时间单位面积上损失的质量;为颗粒的径粒函数;a为颗粒对壁面的冲击角;为冲击角函数;v为颗粒相对于壁面的速度(m/s);代表颗粒相对速度函数;Aface为壁面面积(m2)。
3 物理模型及网格划分
3.1 物理模型及计算设置对CJC601-L-45/2X3.5 的模型冲击式水轮机单喷嘴进行三维建模。该模型水轮机参数如下:设计水头为32 m,设计流量为0.038 m3/s,额定出力为10 kW。为了使数值模拟的结果更加明显,采用小开度进口。进口直径为125 mm,进口面积为0.012 m2,为了深入研究自由射流的流动特性,将喷嘴出口的射流域以圆柱代替。
计算设置:水和空气视为连续相,水气两相流进行三维瞬态计算,时间步长设置为0.005 s。采用RNGk-ε紊流模型,开启VOF模型捕捉水气边界,使用隐式算法,通过隐式体积力(implicit body force)来平衡压力梯度和动量方程中的体积力,以提高解的收敛。求解方法采用SIMPLIC算法,离散格式选用一阶迎风格式。在设置松弛因子时,将Momentum 改为0.2,以提高残差中连续性一相的收敛性,其余值保持默认。由于非定常流动的Fr和We都比较大,重力和表面张力对主流特性的影响小[21],因此本文在计算过程中忽略这些力的影响。
当水气两相流完全收敛,流场稳定之后,增加泥沙颗粒,泥沙颗粒形状默认为球形颗粒,选择面入射,入射方向为法向。泥沙密度为2650 kg/m3,体积分数为1%,对应的泥沙入口质量为0.263 kg/s。对水气沙三相流进行非稳态计算。
欧拉-拉格朗日法的计算过程:水相和气相视作连续相,在欧拉场中用统一的运输方程计算,在拉格朗日坐标系下对流场中的每一个颗粒轨迹进行追踪。每一步,离散相求解器都计算颗粒从当前状态起在积分时间内的运动轨迹及动量、质量和能量损益,并更新颗粒状态。每一个连续相时间步对颗粒进行一次更新计算,连续相迭代与离散相计算交替进行,颗粒不断向前推进[16]。在求解过程中,连续相与离散相是单项耦合的,即连续相在当前时间步的计算结果会作为离散相下一个时间步计算时的输入条件,从而影响离散相的分布和流场,而连续相的流动则不受泥沙颗粒存在的影响。
3.2 边界条件水气两相流边界条件及泥沙颗粒入射的边界条件设置如图1所示。
(1)入口边界。水流入口边界设置为速度入口,流速大小根据模型实验,设置为0.857 m/s。空气入口边界设置为压力进口,相对压力为0。泥沙入口边界亦设为速度入口,速度大小与清水相同。
(2)出口边界。出口边界采用压力出口边界,相对压力为0。
(3)壁面。所有壁面均为无滑移固体边界,并使用标准壁面函数法来模拟近壁面区域的流动。
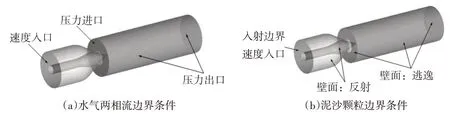
图1 模型边界条件设置
3.3 网格划分及网格无关性分析在ICEM中对模型采用六面体结构化网格划分,如图2所示,对喷嘴出口位置进行局部加密。在计算磨损的过程中,磨损量会受到网格数量的影响,因此需要进行网格无关性验证。表1给出了模型验证的几种不同网格数量。

图2 模型的六面体结构化网格

表1 网格划分
对表1中的5个模型先进行两相流计算,流场稳定后加入离散相继续计算5 s,可得到如图3所示的网格单元数与磨损率的关系。随着网格单元数的增加,入射面的网格数也随之增加,发射的粒子数量也相应增多,从而影响喷射机构的磨损率。随着网格数量的增加,磨损率呈下降趋势;当网格数增加到某一定值后,磨损率则趋于稳定。
除了对磨损率进行网格无关性验证外,还需要Roache[22]引入提出的网格收敛指数(Grid Convergence Index,GCI)对网格的独立性做进一步检查。对model 1,model 2,model 3的网格进行验证,具体验证过程参考文献中的方法[23-25],验证结果如表2。
其中,下标1 ~3分别表示model1,model2,model3三套由疏到密的网格。rk,k+1为网格细化比,为网格控制单元数;δk,k+1为不同网格之间的相对误差,;fk取不同网格下质量流量的收敛解(kg/s);p为收敛精度,可用不动点迭代法求解;在计算GCI时,Fs为安全因子,基于三套网格取值,Fs取1.25。
可以看出,model 2和model 3之间的网格收敛指数为0.63%,说明model 3已经满足精度要求。结合对磨损率进行的无关性验证,加之考虑到计算资源的问题,在本文之后的计算中,都选用model 4,即2 586 116的网格单元数进行计算,此时,进口面的网格共发射粒子数为66 000。
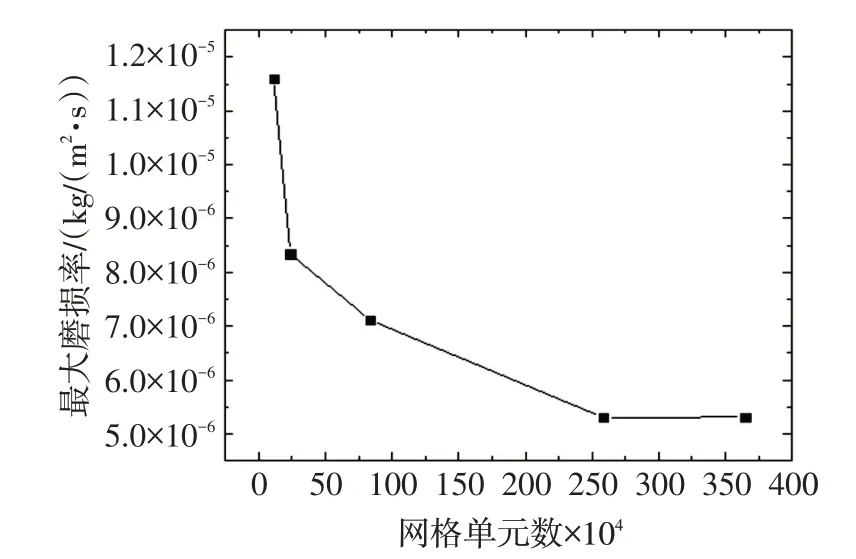
图3 网格无关性验证

表2 网格独立性验证(GCI)
4 结果及讨论
4.1 流动数值结果分析图4为非稳态气液两相流的数值模拟结果。在图4(a)中可以看出,水流在流动到接近喷嘴出口位置时,流速开始增加;流速在喷嘴出口处达到最大值,为36 m/s;之后,水流与射流机构碰撞,流入大气。随着水流与空气不断接触,部分空气卷吸、混掺入高速射流中,并获得动能,随水流一起向前流动,使得流速降低[26]。图4(b)为水进入射流域后的体积分数云图,不考虑重力作用,水流呈轴对称分布。这与Zeng等[27]的研究结果较为一致。水流的对称性与射流质量关系密切,偏心流会使射流发散,降低机组效率[28]。图4(c)中,进口处压力为566 kPa,随着水流接近喷嘴出口,压力迅速减小。这表明在喷嘴出口位置,大部分压能转换成了动能。
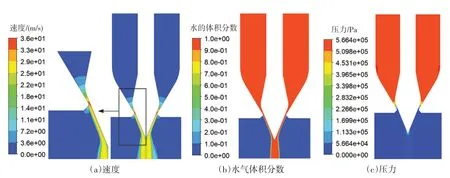
图4 两相流的速度、水气体积分数及压力分布云图
4.2 颗粒直径对磨损的影响水流在流经喷嘴收缩段时会加速,高速射流中所携带的泥沙颗粒会撞击喷嘴和喷针表面,造成材料剥蚀。喷针的磨损会增加水流在一定开度下的过流面积,当喷针磨损比较严重的时候,即使机组是关闭的,也会有水流泄出,从而对整个机组的控制系统造成负面影响。泥沙颗粒直径与喷射机构表面的撞击位置和磨损量有着直接的关系,因此本文选择了几种不同的泥沙直径作为研究对象,探讨其对喷射机构磨损的影响。
如图5所示,图5(a)为清水的流场流线,图5(b)—(f)为不同泥沙颗粒直径的轨迹线。在喷嘴进口至过渡处之前的水流段,流场流线与喷针轴线平行;加入泥沙之后,轨迹线与流线并不重合,且随着泥沙颗粒直径的增加,轨迹线的不平行数越来越多,说明泥沙颗粒直径越大,随流性越差。在过流面积减小的过渡段,由于喷嘴突然收缩,而颗粒轨迹又与流线不重合,此时,泥沙颗粒会与喷针和喷嘴表面发生剧烈碰撞,导致喷嘴收缩段更易受到磨损。在射流流出喷嘴之后,泥沙颗粒会受到惯性力和离心力的影响,随着泥沙直径的增加,轨迹线向着喷针轴线的弯曲倾斜程度也随之增加。

图5 流场流线及不同泥沙颗粒直径的轨迹线
经过以上分析,可知泥沙颗粒与喷嘴的碰撞磨损主要发生在喷嘴的过渡段。图6为不同泥沙径粒下的喷嘴表面磨损率云图。从图6可以看出,当泥沙颗粒直径为0.01 mm和0.05 mm时,喷嘴的磨损范围较小;当泥沙颗粒直径增大到0.4 mm和1 mm时,喷嘴的磨损范围显著增加。但是喷嘴的磨损位置都是相似的。这表明泥沙颗粒的大小虽然会影响喷嘴磨损的范围,但对喷嘴表面的磨损位置影响较小。且喷嘴的磨损形态主要为点状和片状磨损。
图7(a)为某电站喷嘴磨损实物图[6],可以看出,喷嘴接近出口处的位置更易受到磨损,数值模拟的结果和现场磨损的结果较为一致,验证了数模的准确性。
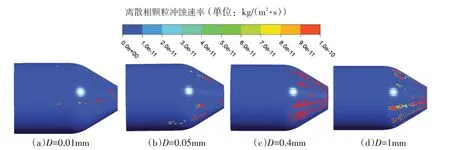
图6 不同泥沙直径下的喷嘴磨损率云图

图7 某电站喷嘴及碰嘴泥沙磨损图[6]
图8为喷针受到不同径粒泥沙磨损的磨损率分布云图。当泥沙径粒为0.01 mm时,由于细小的颗粒随流性较强,在喷针直杆段、过渡段和喷针头部的针尖位置均有磨损;当泥沙直径开始增加,其随流性越来越差,泥沙颗粒在流动过程中,会不断撞击喷针杆部和喷针颈部,而在喷针头部的针尖位置,由于大颗粒受到的离心力更大,将颗粒甩离针尖表面,因此针尖部位反而不易受到磨损;随着颗粒直径的增加,喷针直杆段的磨损会由于颗粒的离心力使颗粒偏离而减弱,而喷针颈部过渡段的磨损则会由于占主导因素的惯性力作用而增加。因此,喷针头部的针尖位置更容易受到细小颗粒的磨损,而喷针过渡段的磨损与颗粒直径大小呈正相关。对于模型冲击式水轮机而言,水头和流速都远小于真机,此时的数值模拟,显示的喷针位置磨损形态主要为点状。对比图7(b)(c)(d),为某一高水头电站喷射机构磨损的实物图[6]。由于高水头、高流速,针尖位置磨损更为严重,且磨损形态主要为波纹状。
4.3 颗粒浓度对磨损的影响河流中的携沙量常受到径流量、干旱指数和人为活动等因素的影响,因此,研究泥沙颗粒浓度对射流机构磨损的影响有着重要的意义。

表2 不同泥沙浓度下喷射机构的磨损率
在计算稳定后的连续相中分别加入不同浓度的泥沙颗粒(泥沙的体积分数分别为1%、2%、3%,4%和5%),继续计算0.45 s 后,可以得到如图10 所示的喷射机构磨损率变化曲线。从图10 可以发现,随着泥沙浓度的增加,喷嘴和喷针受到的最大磨损率几乎呈线性增加;结合表2,可以看出,在同一泥沙浓度下,喷嘴受到的磨损要大于喷针受到的磨损;结合图6(c)、图8(b)和图9可知,泥沙的浓度增加,对泥沙颗粒的运动轨迹以及喷针表面磨损的位置影响不大。
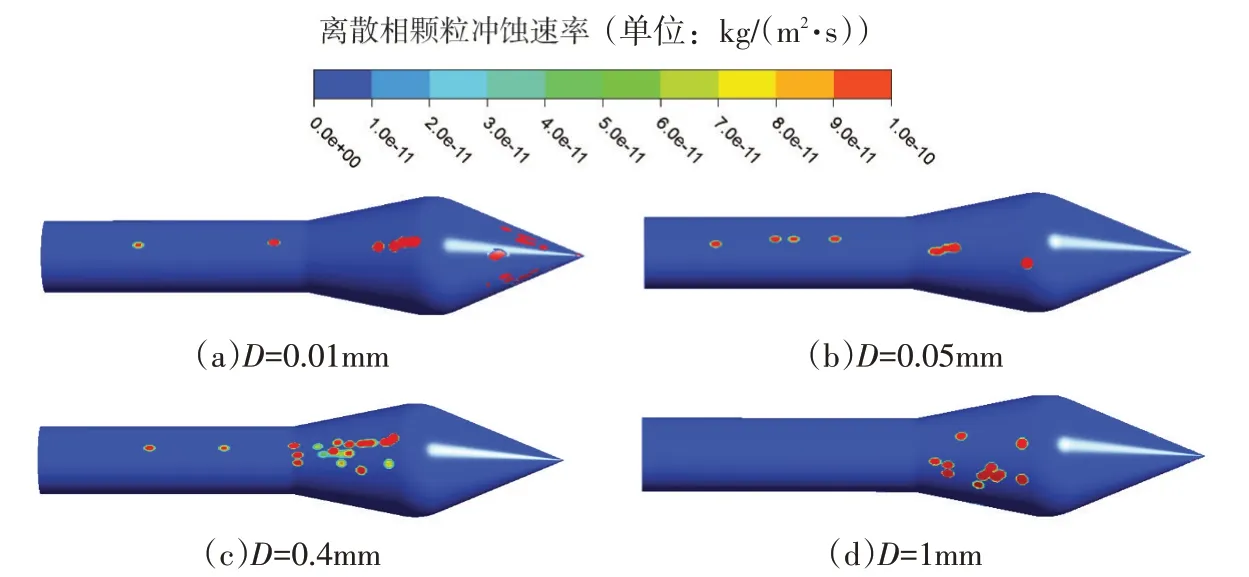
图8 不同泥沙直径下的喷针磨损率云图

图9 D=0.05mm,泥沙浓度为5%时的泥沙颗粒轨迹线及喷针磨损云图

图10 喷嘴和喷针最大磨损率随泥沙浓度的变化
5 总结
本文对冲击式水轮机的喷射机构进行了水气沙三相非定常计算,研究了泥沙颗粒的直径和浓度,对喷嘴和喷针磨损位置、磨损率的影响。数值模拟的结果和现场磨损的结果较为一致,验证了数模的准确性。本文研究为机组的检修维护和安全稳定运行提供了参考和理论依据。主要结论如下:(1)不考虑重力,水流呈轴对称分布。喷嘴出口处流速达到了最大值,同时压力出现最小值,这表明喷嘴出口处的压能大部分转化为了动能。(2)泥沙颗粒直径越大,随流性越差。泥沙颗粒的大小会影响喷嘴的磨损范围,但喷嘴表面的磨损位置是相似的,喷针头部的针尖位置更容易受到细小颗粒的磨损,喷针过渡段的磨损程度与颗粒直径大小呈正相关。(3)喷嘴和喷针受到的最大磨损率会随着泥沙浓度的增加而增大;在同一泥沙浓度下,喷嘴受到的磨损要大于喷针;泥沙浓度的增加,会影响磨损率,但对泥沙颗粒的运动轨迹及喷针磨损的位置影响不大。

