多目标约束下的土石坝抗液化措施数值建模与优化分析方法
李明超,杨 琳,任秋兵,赵 宇
(1.水利工程仿真与安全国家重点实验室,天津大学,天津 300350;2.天津水务投资集团有限公司,天津 300200)
1 研究背景
地震是一种影响极大的自然灾害,同时会伴随着严重的次生灾害,其中地基液化问题较为突出。土石坝作为当今应用最广泛的坝型,其坝基液化问题不容忽视。一旦坝基发生液化,土体中的孔隙水压力短时间内迅速升高,有效应力急剧降低,土体的抗剪强度严重削弱,导致沉降不均匀、地基失效、坝体滑坡、土坝溃决等一系列灾害,对地基、岸坡和坝体等造成极大的破坏[1]。
在目前的土石坝工程中,对于可能发生液化的土层,常常采用挖除、置换、压重等处理措施[2]。在已有工程中,长河坝砾石土心墙堆石坝挖除坝基几十米埋深范围内的可液化砂层;黄金坪沥青混凝土心墙堆石坝的基础液化砂层基本挖除,并在下游设置压重。设置压重增加了坡脚下的竖向应力,提高了坝基土的抗液化能力;同时也增大了坝体和坝基的整体抗滑稳定性,防止了坝基土体从坡脚挤压而出。该方式施工简单,且可以利用开挖的土石料,造价低,经济有效,因此被广泛用于我国的中小型土石坝的坡脚加固[3-4]。
近年来,针对土石坝抗液化措施的分析国内外进行了很多研究。Mulunda等[5]主要通过改善液化土的性质和初始应力来控制液化,提出了地表开挖回填、设置压力平台、防渗平台和加强排水设计等液化控制措施;付磊等[6]采用拟静力法和动力反应分析法相结合确定土石坝深水条件下抛石压坡的抗震加固断面;Ye等[7]利用大坝自重固结来提高土石坝抗液化性能,并使用有效应力方法来分析了液化修复的效果;高大水等[8]采用动力有限元分析对花凉亭工程上游坝坡帮坡压重抗震加固方案进行技术论证,有效解决了水库蓄水条件下的大坝抗震加固问题;岑威钧等[9]根据地基液化深度确定液化水平影响长度,再进行不同填土厚度下抗震效果分析,最终确定了安全经济的压重平台厚度和长度。Zhang等[10]探讨了土石坝压重平台的长度、高度和材料内摩擦角对土石坝静动力特性的影响,并给出了建议的取值范围;Amin 等[11]进行稳定渗流条件下Siahoo 大坝的地震动力分析,识别地基的液化区并采用应力重分布方法估计震后位移;Kazunari 等[12]提出了一种根据地质统计参数及地震参数的土石坝液化概率计算方法,并应用于实际设计问题中;王富强等[13]分析了孔隙水转移对液化土层强度和变形的影响,提出了坝基覆盖层地震液化的挖除置换、加密、压重等工程措施;Hadi 等[14]通过振动台试验研究了橡胶排水柱和碎石排水柱对饱和砂土液化势的影响,表明密实度是控制液化的最重要因素;Liam Finn[15]综合萨迪斯大坝等多个工程,提出了一套包括性能标准选择、分析程序及非线性动力本构的液化场地土石坝设计方法。
然而,已有研究主要是根据工程经验确定土石坝抗液化措施的方案,目前在抗液化措施效果优化方面的研究较少。现有工程中,主要根据设计人员经验选取主要设计参数,没有具体的理论设计指导,若参数选择过于保守,则增加工程投资,延长工期,增加了施工难度;若参数选择过于经济,则仍然存在土石坝安全隐患。因此,若能提出一套可以综合考虑安全性和经济性的土石坝的抗液化措施优化设计方法,实现对土石坝抗液化措施的定量化、精细化设计,具有重要意义和实践价值。
针对复杂的工程优化问题,作为常用的机器学习算法之一,遗传算法(Genetic Algorithm,简称GA)通过建立对应具体问题的适应度函数并利用遗传算子联合搜索的方法求解最优解,具有原理简单、适应性广的特点,在工程优化领域逐渐得到广泛应用。由于工程中优化问题常常需要考虑成本和效果的平衡,一般都属于多目标优化问题。多目标遗传优化算法作为一种群体优化算法,对多目标优化问题的求解与传统优化方法相比有明显优势[16]。例如,谌文武等[17]提出一种以性价比为评价指标,运用快速拉格朗日差分分析和遗传算法对斜坡加固方案进行优化的新方法;官夏菲等[18]采用SVR 回归模型建立优化变量(跌坎高度d、突扩比β和尾坎坡度θ)与优化目标(消能率ΔE/E1、临底流速v)之间的近似模型,并采用遗传算法求解该近似模型,对消力池体型进行优化;Trung-Thanh[19]等通过存档微遗传算法(Archive-based Micro-Genetic Algorithm,简称AMGA)与克里金模型的结合对加工参数进行优化,改进了铣削过程。
总的来说,目前工程抗液化措施主要根据经验设计,尚未建立定量的土石坝抗液化措施优化分析方法。因此,本文有针对性地开展了多目标、多约束条件下综合安全性与经济性的土石坝抗液化措施数值优化研究。以坝体坡面水平位移梯度、坝顶震陷和抗液化措施成本最小化为优化目标,以静动力抗滑稳定安全系数、地基最大液化范围、液化深度、典型点地震过程中平均液化度和震后永久水平位移为约束条件,建立土石坝抗液化措施多目标优化数学模型;进而通过VC++集成有限差分法软件FLAC3D进行开发,运用完全非线性动力算法和多目标遗传算法对该数学模型进行求解,并将其应用于工程实例,为改善土石坝坝基液化问题提供新的手段。
2 研究方法框架
综合考虑经济性和安全性,根据压重平台和地基置换的特点建立相应的多目标优化数学模型,采用多目标遗传优化算法AMGA进行求解,对压重平台和地基置换的设计参数进行优化,研究框架如图1所示,主要包括以下内容:
(1)根据以往工程经验,确定需要优化的设计参数(压重平台的长度、高度和坡度以及地基置换的深度和位置等),基于工程资料确定参数变量空间,即参数的取值范围。优化过程中,算法在该范围中生成设计变量的方案。
(2)基于设计变量方案,进行参数化建模并采用FLAC3D进行土石坝静动力计算及坝基液化的分析。首先实现了土石坝填筑及蓄水的静力模拟,在此基础上分别进行了安全系数及动力部分的计算。安全系数包括静力抗滑安全系数及拟静力法动力抗滑安全系数,在动力计算中编写了坝基液化监控程序,计算得到坝基的液化程度、范围等情况。
(3)综合考虑经济性与安全性,选取坝体坡面水平位移梯度、坝顶震陷与抗液化措施方案的造价作为优化目标,从地基液化程度、液化范围及大小、静动力抗滑稳定安全系数、坝体永久变形的方面给定约束条件,建立土石坝抗液化措施的多目标优化数学模型。
(4)运用多目标遗传算法AMGA 控制求解上述流程。通过VC++集成FLAC3D 进行开发,实现算法自动搜索设计变量空间,控制FLAC3D进行土石坝静动力及坝基液化的计算,并在后处理程序中计算目标函数及约束条件,多次迭代直至算法收敛。该算法将求出一组Pareto 解集,根据工程需要从求出的Pareto 解集中选取最优解。将该优化方法应用于工程实例,实现对某土石坝抗液化措施的多目标优化,并通过对比分析验证了该方法的有效性。

图1 研究方法总体框架
3 土石坝抗液化措施多目标优化数学模型
(1)确定设计变量及变量空间。以土石坝工程中采用压重平台及地基开挖置换措施为例,选取9个控制性设计变量,见表1和图2。具体的参数空间,即每个变量的变化范围及初始值,需根据特定的工程确定。
(2)给定约束条件,选取优化目标。常见的单目标坝体优化主要是以满足安全性指标为约束条件,以降低工程造价为优化目标,这种方法会倾向于方案的经济性,土石坝的抗液化方案应该综合考虑安全性和经济性两方面的目标,优化方案应在两者之间寻找平衡。地震导致的土石坝坡面裂缝可能会导致渗漏等现象,从而严重危害坝体安全,常用坝体坡面位移梯度作为土石坝安全评价指标。液化过程中,土体由于抗剪强度的降低,常常出现侧向大位移,而液化结束后,可液化土体由于震动变得密实,往往出现大沉降[20],坝顶震陷也常常作为评价土石坝抗震性能的重要指标[21]。因此安全性目标与约束条件将从震中与震后两方面选取。

表1 设计变量

图2 设计变量
通过前期试算已知,地震过程中,由于上游库水压力的作用,上游坡面水平位移的最大值通常出现在上游压重平台与坡面接触点处,而下游面上水平位移分布从坡脚到坡顶呈现逐渐减小的趋势。这里将安全性指标选取为:地震过程中上游面平台接触点与坝体坡脚及坡顶水平位移差值之和的最大值G1;地震过程中下游面坝体坡脚与坡顶水平位移最大差值G2;坝顶中心震后永久沉降Z。
此外,出于减少工程成本的考虑,设置压重平台与地基开挖置换的断面总面积A为经济性指标,且考虑到筑坝的成本高于地基处理的成本,将其体现在该指标中:
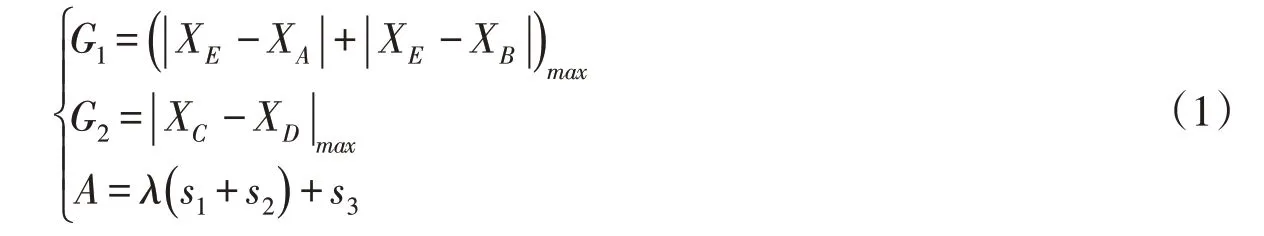
式中:A、B、C、D、E点分别为上游坡脚、上游坡顶、下游坡顶、下游坡脚和上游面平台与坡面接触点;XA、XB、XC、XD、XE分别为A—E点的地震过程中水平位移;s1、s2、s3分别为坝前压重平台、坝后压重平台和地基置换断面的面积;λ为压重平台与地基处理的每平方米成本单价之比,需根据工程实际确定。
优化目标即为使4个指标G1、G2、Z、A最小化,在优化过程中,根据不同目标的重要性,对每个目标定义权重或比例因子。在设置约束条件时,除根据工程需要设置指标G1、G2、Z和A的约束条件,首先在静力分析的基础上,设置坝体静动力抗滑稳定安全系数的约束条件;其次在动力分析中为了同时实现对地基液化的控制,除计算整体地基液化面积及深度以外,在坝体下方设置两个监测点,监测并计算整场地震过程中该点液化程度并取平均值作为该点平均液化度,对此设置约束条件。此外,为了控制震后坝体永久变形,对上下游坡脚坡顶的水平绝对位移均设置约束条件。
(3)将上述优化设计的数学模型表示为:
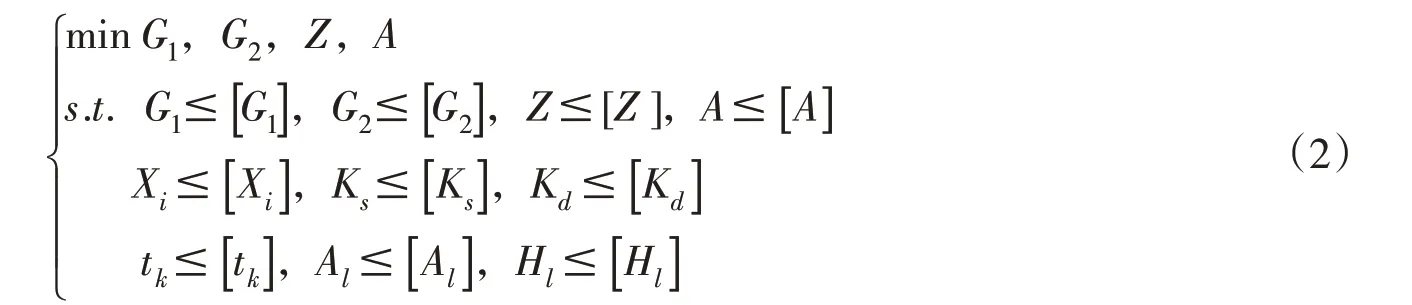
式中:[Xi],i=a,b,c,d分别为各点水平震后永久位移限制条件;[Ks][Kd]分别为坝体静力抗滑稳定安全系数限制条件及拟静力法计算的坝体动力抗滑稳定安全系数;[tk],k=1,2为两个坝基监测点的地震过程中平均液化度限制条件,分别位于上下游坡脚下方坝基深2 m处;[Al][Hl]分别为地震过程中坝基最大液化面积及液化深度。
4 模型求解方法
4.1 存档微遗传算法由于遗传算法具有自适应性,是一种采用群体搜索策略的全局概率优化算法,它可以不了解问题的内在性质,而直接操作结构对象,目前在多目标优化问题中被广泛应用[22]。作为一种非归一化的多目标优化遗传算法,存档微遗传算法(AMGA)非常适合高度非线性、非连续、非凸及高度约束的搜索空间,适用于有多个局部最优的函数。由于本文中模型设计变量众多,变量与目标间关系复杂,非线性程度较高,因此选用该算法进行优化。
在多目标优化问题中,采用支配关系评估不同方案结果的优劣。在AMGA算法中,对每个目标参数分别进行变异和交叉标准遗传操作,选择过程使用三层机制。第一层适应度是根据解在种群中的支配水平来分配的,主要通过设置存档来进行。第二层适应度的根据为目标方案对算法搜索历史的贡献程度,第三层适应度以种群的多样性为主要考虑因素。因此,AMGA 算法在进化过程之外还需要设立一个存档,使得档案中的个体在进化过程中始终保持非支配的地位[23]。
4.2 集成FLAC3D的土石坝抗液化措施优化流程在整个优化流程中,需将FLAC3D作为一个子程序调用,故AMGA优化算法与FLAC3D的串接是关键问题。整个流程通过VC++控制实现,并编译成exe文件,具体思路如下:
(1)在优化控件中设定AMGA算法参数、设计变量及变量空间、约束条件、权重与比例因子、目标函数等;该控件在每一代的进化中输出设计变量数值,存入txt文件;
(2)调用前处理exe读取存放设计变量的txt文件,生成参数化建模的命令流txt文件;
(3)利用创建子进程的方式在VC++中调用FLAC3D.exe,并控制其依次读取命令流文件、自编的液化指示器dll文件以及地震波文件;
(4)FLAC3D进行静动力计算。在静力计算的基础上,利用强度折减法进行安全系数的计算;动力计算中,在坝体上设置a—e五个坝体监测点,监测地震过程中的水平位移值,并在每一时步计算坝基液化范围、深度及坝基液化监测点的超孔压比;
(5)计算结束后,利用hist命令提取上述监测值,并读取安全系数、上下游坡顶坡脚的震后永久水平变形、坝顶震陷量,存入相应结果txt文件;
(6)结束FLAC3D子进程,在VC++主进程中,调用后处理exe,读取(5)中结果txt 文件,计算平均液化度,提取各约束指标值,同时计算目标指标G1、G2、Z和A的数值,存入存放目标函数及约束指标的txt文件;
(7)将(6)中目标函数及约束指标输入到优化控件中,判断是否满足各约束条件,进行下一代计算。重复步骤(2)—(7),直至算法收敛。上述流程如图3所示。

图3 集成优化流程
5 工程实例分析
5.1 数值模型建立某水库工程是天津市南水北调中线配套工程的重要组成部分[24]。该工程的围坝型式为复合土工膜防渗斜墙土石坝,总坝长6570 m。选取某典型断面进行计算,断面坝高8.6 m,坝顶宽度8.0 m,上游临水面坝坡坡度为1∶3.0,坝高6.5 m处设置了2.0 m宽的马道,下游背水侧坝坡坡度为1∶3.0。由于围坝长度方向的尺寸远大于横断面尺寸,把该模型按平面应变问题处理,整体厚度方向为1 m。计算中采用正常运行水位水深为6.0 m。土石坝模型地基截取长度一般取0.3 ~0.5 倍的坝体顺河向底部长度[25],地基深度取30.0 m,模型总长度为173.5 m。上游坡脚开挖锚固槽进行坝基防渗处理,槽深约2.5 m,槽底宽度4.0 m,上游临水侧坝坡设置约0.5 m的钢筋混凝土板护砌、垫层及复合土工膜,建模过程中将其简化为整体护砌。
该工程坝基15 m范围内存在两层大范围的液化土层,表层粉土分布连续,第二层液化土层埋藏较浅且上下游贯通,坝基液化问题较为突出。为减轻地震液化的影响,该工程采用挖除置换表层可液土体结合压重平台的处理方案,坝后压重平台坡面坡度为1∶1,高3.0 m,宽12.0 m,坝前压重平台坡面坡度为1∶1.17,高2.50 m,宽15.0 m,挖除表层2.1 m 的可液化粉土。所建立的模型如图4 所示,模型中材料参数见表2。

图4 工程实例模型示意图

表2 材料参数
工程抗震设防烈度为Ⅶ度,库区地震峰值加速度为0.15g。由于该工程的抗震设防烈度低于Ⅷ度,因此数值模拟计算中仅考虑水平地震作用。文中输入的地震波(见图5)为滤波及基线调整后的某南北水平向的天津波(1976年)。
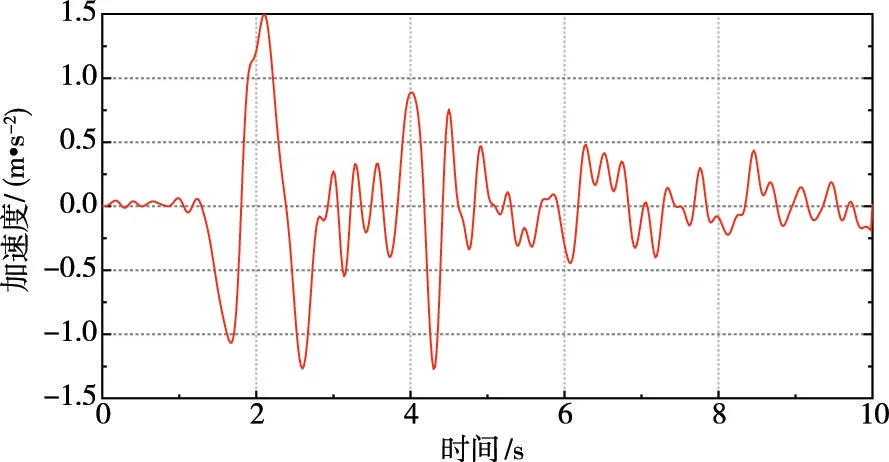
图5 输入地震波
5.2 静动力数值计算计算中编写了Fish 函数进行参数化建模。读取优化设计变量后,判断坝前压重平台高度和坝后压重平台高度相关关系,以此决定不同的坝体分块划分方法。该方法可使相邻块体接触面长度、网格数量和比率相等,以满足接触面连续性的要求,同时控制整体模型网格尺寸相似并满足动力计算的要求。该参数化建模流程仅需输入设计参数即可实现,便于在优化过程中调用。
土石坝模型的数值计算包括静力和动力计算两部分。静力计算包括坝体填筑及蓄水的模拟,其目的主要是为确定动力计算初始的应力场和渗流场。模拟得到大坝施工填筑完成后的最终沉降为57.96 cm。在围坝坝段的实测数据中,18个坝体断面施工期和沉降期的总沉降量平均值为52.83 cm,仿真结果与实测结果是一致的,表明了所建立模型及边界约束条件的合理性。
动力计算流程包括在震前初始状态的基础上,设置自由场边界及阻尼[26],输入地震波,并完成流固耦合计算。其中,采用Finn 模型模拟在动力作用下可液化土体的孔压积累直至土体液化的过程,该模型假定动力作用中孔压的上升与塑性体积应变增量相关,增加了动孔压的上升计算,孔压上升到一定程度后,土体发生液化。采用有效应力法进行一般应力条件下可液化土体的液化判定。为了便于衡量土体液化的程度,在数值计算中引入超孔压比的概念。将超孔压比定义为[27]:

根据上述原理,利用Fish语言编写了超静孔隙水压力和超孔压比的监测程序。利用自定义单元额外变量在每个计算步中计算各点的超静孔隙水压力和超孔压比,进而通过数据处理得到每个点的液化时长。利用C++语言编写液化指示器。设置临界超孔压比为0.6,对于可液化土层,计算过程中当单元超孔压比超过临界超孔压比,单元状态将显示为“液化中”,记录每一时刻的液化中单元总面积及最大深度。最后将该C++项目文件编译成dll文件,以便计算时在命令流中直接调用。
采用初步抗液化方案后,地震过程中上游坡脚残余水平变形为29.88 cm,下游坡脚残余水平变形为43.79 cm,液化土层在地震强度较大时出现大范围液化,引起较大的坝体变形。因此,需要开展土石坝抗液化措施优化研究。
5.3 抗液化措施多目标优化分析结合初步抗液化方案设置设计变量空间,见表3,表中坐标值均为相对于模型零点的数值;地面高程为30 m,λ取1.5。优化中需对目标定义合适的权重与比例因子,将各目标数值统一在相似水平[28]。

式中:Xi和为各目标调整前后的数值;Wi为各目标对应的权重因子;SFi为各目标对应的比例因子。通过前期试算,确定权重与比例因子见表4。根据初始方案计算结果给定目标、液化、安全系数与残余变形的约束条件。

表3 设计变量约束及优化结果

表4 目标函数参数及优化结果
采用AMGA 算法对多目标优化数学模型进行求解。种群规模设置为40,进化到第129代算法达到收敛。经过三次计算,AMGA算法平均寻优率为40.63%,相较于常用的第二代非劣排序遗传算法(NSGA-Ⅱ)的三次平均寻优率85.49%,其收敛性相对较差,但其探索能力强,搜索并不集中局部最优解,得到的优化方案效果也更好,较为适合本文的设计变量较多及多峰情况的数学模型搜索。由算法搜索得到的解集的目标函数分布如图6所示,并根据约束条件及目标函数得出Pareto前沿。由图可知,AMGA 算法前进性较强,在Pareto 前沿处探索较为密集,且Pareto 前沿呈现出两两制约关系,难以同时达到最优,需要根据工程实际在Pareto前沿中选择优化方案。
舍去不满足各约束及取值较为极端的方案,得到的最终方案见表4。从选取的优化指标来看,坝顶震陷有了较大改善,震陷量减少了13.22 cm,优化幅度达到21.03%;坝体上下游面的水平变形梯度较初始方案均有改善,分别减少了16.59%和24.33%,坝体安全性得到提高;抗液化措施成本优化明显,降低了18.53%,经济性得到了改善。优化前后的G1、G2及Z的时程如图7所示,在地震过程中,G1、G2及Z的数值均是不断发展的,下游坡面水平位移梯度较大,震后为坝体坡面变形梯度最大的时刻。采取优化方案后,上下游坡面坝体位移梯度在整个地震过程中均得到了控制。从图8中可以看出,坝体深层滑动趋势向后移动,并未贯穿至上游坡面,且下游坝体下方水平位移明显减少,未形成完整滑动面,坝体变形及整体抗滑稳定得到改善。震后沉降主要集中在上游坝体,整体沉降量明显减少。
各点残余变形及平均液化度见表5。其中,采取初始方案后震后上游坡脚出现了79.85 cm的较大沉降,下游坡脚出现了43.79 cm的较大水平变形,结合图8,坝体出现向下游的深层滑动。采取优化方案后,坝体下方深层滑动趋势有所降低,坝体下方偏下游的位置位移控制较为明显。优化方案满足了残余变形、平均液化度、最大液化面积、液化深度及安全系数等各项约束条件,并有了一定程度的改善,其中对水平残余变形的改善最为明显。

图6 算法搜索结果及Pareto前沿分布

图7 优化前后G1、G2、Z时程图
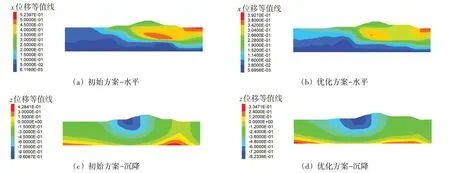
图8 优化前后残余位移云图(单位:m)

表5 各约束条件优化结果
图9显示下游液化监测点的超孔压比明显高于上游监测点,优化前后下游监测点的最大超孔压比为0.983和0.724,震后超孔压比分别为0.484和0.431,存在液化的时刻,上游监测点最大超孔压比分别为0.340和0.273,震后超孔压比分别为0.086和0.015,地震过程中并未发生液化。下游的液化程度更大,与图8中下游水平位移较大相对应。采用优化方案后,两个监测点在地震过程中超孔压比的发展均有了一定程度的改善,平均超孔压比分别由0.115和0.578降至0.095和0.430,坝基最大液化面积也从1618.59 m2降低到了1560.32 m2,表明了优化方案对于坝基液化问题的有效改善。

图9 优化前后超孔压比时程对比
6 结论
针对目前工程中主要依靠经验进行土石坝抗液化措施设计的现状,提出了一种考虑多目标、多约束条件下的土石坝抗液化措施数值建模与优化分析方法。该方法以坝体坡面水平位移梯度、坝顶震陷和抗液化措施成本最小化为优化目标,以静动力抗滑稳定安全系数、地基最大液化范围、深度、典型点平均液化度和坝体永久水平变形为约束条件,建立了相应的数学模型,运用完全非线性动力算法和多目标遗传算法对土石坝的压重平台和坝基置换参数进行优化设计,实现了综合考虑土石坝抗液化措施的安全性能与经济效益。该方法应用于工程实例,对工程中压重平台及地基置换的9个控制性设计参数进行优化,最终方案坝体水平位移指标G1较初始方案降低了16.59%,水平位移指标G2较初始方案降低了24.33%,坝顶沉降指标Z较初始方案降低了21.03%,节约成本18.53%,坝基液化与震后残余变形均得到了一定改善。
传统的土石坝抗液化方案设计方法存在主要根据经验设计、不能定量化分析、易造成浪费等问题,所提出的综合考虑安全性和经济性的土石坝的抗液化措施优化分析方法,初步实现了对土石坝抗液化措施的定量化、精细化设计与优化,并可进一步推广应用于地基中存在可液化土的各类建筑工程抗液化措施设计与优化中,具有重要的工程实践价值。
需要指出的是,所建立的优化模型中目标函数及约束条件的权重可根据实际工程需求来进行选取和调整;现有数值模拟中一般采用超孔压比或超孔隙水压力作为液化的标准进行抗液化措施的效果评价,但在实际工程中液化的影响因素众多,不同的液化位置及液化程度对工程安全的影响各不相同,因此该指标与工程安全的具体关系仍有待深入探讨;由于优化模型的目标函数与约束条件众多,导致优化中对算法需要提出更高的要求。因此,后续研究中需要完善地基液化状况的评估方法并提出有针对性的抗液化措施,同时在算法的探索性及并行计算方面需要进一步研究。

