U形渡槽内水体液面晃动对流作用试验研究

王海波，李春雷，张昆航

（中国水利水电科学研究院工程抗震研究中心，北京 100048）

1 研究背景

大型渡槽结构是长距离调水工程的主要建筑物。我国西南高地震烈度区调水工程中大型渡槽抗震安全问题十分突出，对长距离调水工程安全运行至关重要。渡槽结构震后修复难度大于其它交通类桥梁结构，并且因输水线路中水体短时集中倾泻，存在局地引发次生灾害的风险，因此渡槽抗震设计引起社会及建设运营部门的高度重视。槽内水体质量与渡槽槽身结构质量相当甚至更大，不仅占据静态荷载的主要部分，其与结构的流固动态相互作用也对输水建筑物的地震响应产生重要影响。地震条件下因槽身结构运动而导致槽内水体横向运动的流固动态耦合问题的十分复杂。渡槽结构的变形和运动导致槽内水体运动，而槽内水体的运动会对渡槽结构产生反作用，进而改变渡槽结构的地震响应。

在求解容器内水体对容器结构的动力相互作用理论方法中，一般假定水体为理性流体，忽略水体的可压缩性，而容器被视为水体的刚性边界，并假定水体做无旋运动而引入速度势函数［1］。Housner［2］为方便求解容器结构的动力响应，基于刚性矩形容器内的液体受到无质量竖向薄膜约束分割的假定，推导出流体冲击作用的等效质量，基于容器内液面为平面晃动假定推导出对流作用的等效质量及距容器底部的高度，用等效质量弹簧替代液体与容器的动力相互作用。事实上，这一方法将流固问题解耦简化为纯结构动力问题，因此在分析流体-结构动力响应中得到较广泛的应用［3］。文献［4］采用位移有限元法数值模拟计算结果，给出了对应于Housner简化模型的U形渡槽的液面晃动频率、等效质量等的回归公式。我国的《水工建筑物抗震设计标准》（GB51247-2018）中有关渡槽地震响应的分析计算也采用了水体等效质量简化模型［5］。随着数值分析方法的进步及计算能力的提高，也有许多研究通过流固耦合基本方程的数值分析方法，求解计入结构变形的流固耦合问题［6-9］。

针对我国南水北调工程大型渡槽的抗震安全问题，国内研究人员开展了渡槽模型的振动台试验研究，对实际工程的水体-渡槽间的动力相互作用进行深入探讨［10-12］，模型均为矩形断面，几何比尺1/30左右。张林让等［12］研究了地震作用下和正弦波激励下水体与槽体相互作用效应和机理，并将试验结果和Housner简化等效质量模型的计算结果进行了对比，结果表明，由Housner模型计算得到的动水压力远小于试验实测值。

本文结合我国西南滇中调水工程的大型薄壁U 形渡槽，通过振动台模型试验，重点关注大型薄壁U 形输水渡槽流固耦合相互作用。笔者前期主要分析了渡槽结构柔性对流体冲击相互作用的影响［13］，本文将针对液面晃动的对流作用进行成果分析整理。试验在中国水利水电科学研究院5 m×5 m大型振动台上进行。振动台为全数字闭环控制，最大水平向加速度1g，能够准确再现地震运动。

2 试验模型设计和测量

振动台试验模型选取单跨30 m的U形渡槽支座以上部分作为研究对象。模型几何比尺1/10，单跨模型槽身长3.0 m（含6 mm 邻跨槽体的间隙）。为减少渡槽端部约束条件对测试模型段的影响，相邻槽身各取0.5 m 模型长度模拟，模型总长4.0 m，见图1。单跨模型渡槽实测结构重量1.144 t，理论渡槽结构体积为0.4347 m3，对应材料容重2630 kg/m3。渡槽满水状态重量2.1367 t，与空槽重量差的水体重量0.9927 t，理论水体体积0.989 m3，水体实际重量约为槽身重量的86.8%。有关模型制作材料及各物理量的相似比尺以及试验所用支座请参见文献［13］，此处不再赘述。渡槽静态竖向支座力见表1。

试验安装了共5 种，合计122 通道传感器用于测量渡槽及槽内水体的地震响应。各传感器位置详细描述请参见文献［13］。试验数据采集采样频率为1000 Hz。

图1 振动台试验渡槽模型及测点（单位：m）

表1 渡槽静态竖向支座力 （单位：kN）

3 液面晃动频率与阻尼比

试验针对不同水位工况，采用0.1g、0.2g和0.4g三个强度水平、0.1 ～90 Hz频段的稳态白噪声激励，分别测试了模型渡槽的横槽向和竖向稳态响应。白噪声激励的采样频率为1000 Hz，计算用FFT长8192点，对应的频率分辨率为0.122 Hz。对于渡槽结构自振特性的识别，可采用结构顶部的加速度响应传递函数。然而，槽内液体晃动频率远低于渡槽结构自振频率，低频加速度难以获得高信噪比响应信号，因此选用水平横槽向支座力传递函数用于识别槽内水体液面晃动自振特性。但是，0.122 Hz 的频率分辨率在1 Hz 频率范围仅有8 个谱线点，很难准确识别1 Hz 附近液面晃动对应的模态。通过采用频谱细化方法［14］，将低频范围的频率分辨率提高8倍至0.01526 Hz，精确分辨出了液面晃动频率附近的支座力传递特征，与原分辨率传递函数的对比见图2。通过对水平支座力细化频谱传递函数的模态识别分析，获得了两阶液面晃动频率及对应的模态阻尼比（见表2）。随激励水平增加或称液面晃动幅度的增加，晃动频率有微小下降。模态阻尼比均值0.738%。

图2 频谱细化水平支座力传递函数对比

表2 横槽向液面晃动特征频率及阻尼比

由于渡槽结构一阶自振频率（实测水平向约9.2 Hz［13］）远高于槽内水体液面晃动频率、结构模态阻尼远大于液面晃动阻尼，故在非稳态加振记录尾部的支座力变化均源于槽内水体的自由衰减液面晃动，参见图3时程曲线。依据自由衰减波动时程同样可分析计算出液面晃动的基频特征频率和对应的阻尼比［16］。阻尼比ξ按下式计算［15］：

式中Ak、Ak+m分别为第k个和第k+m个自由衰减波动曲线的幅值。

由24条水平向或竖向支座力自由衰减曲线得到的液面晃动频率及阻尼比列于表3，一阶晃动频率均值为1.033 Hz，阻尼比0.763%。一阶晃动频率低于0.4g白噪声激励对应结果约0.3%。

对高度H、底宽2l的刚性矩形容器，在重力场g作用下，依据无漩流体力学方程及液面小幅波动假定推导出的容器液面波动特征频率为：

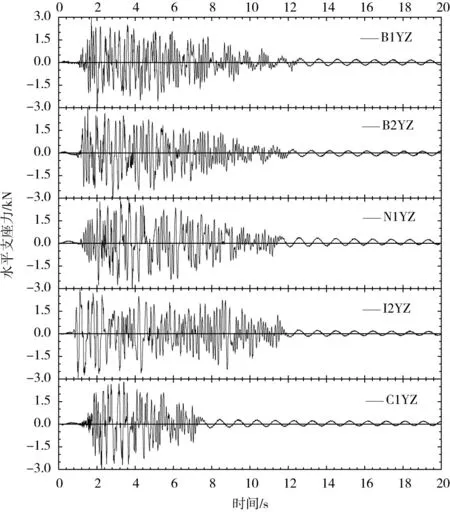
图3 非稳态加振支座力时程曲线

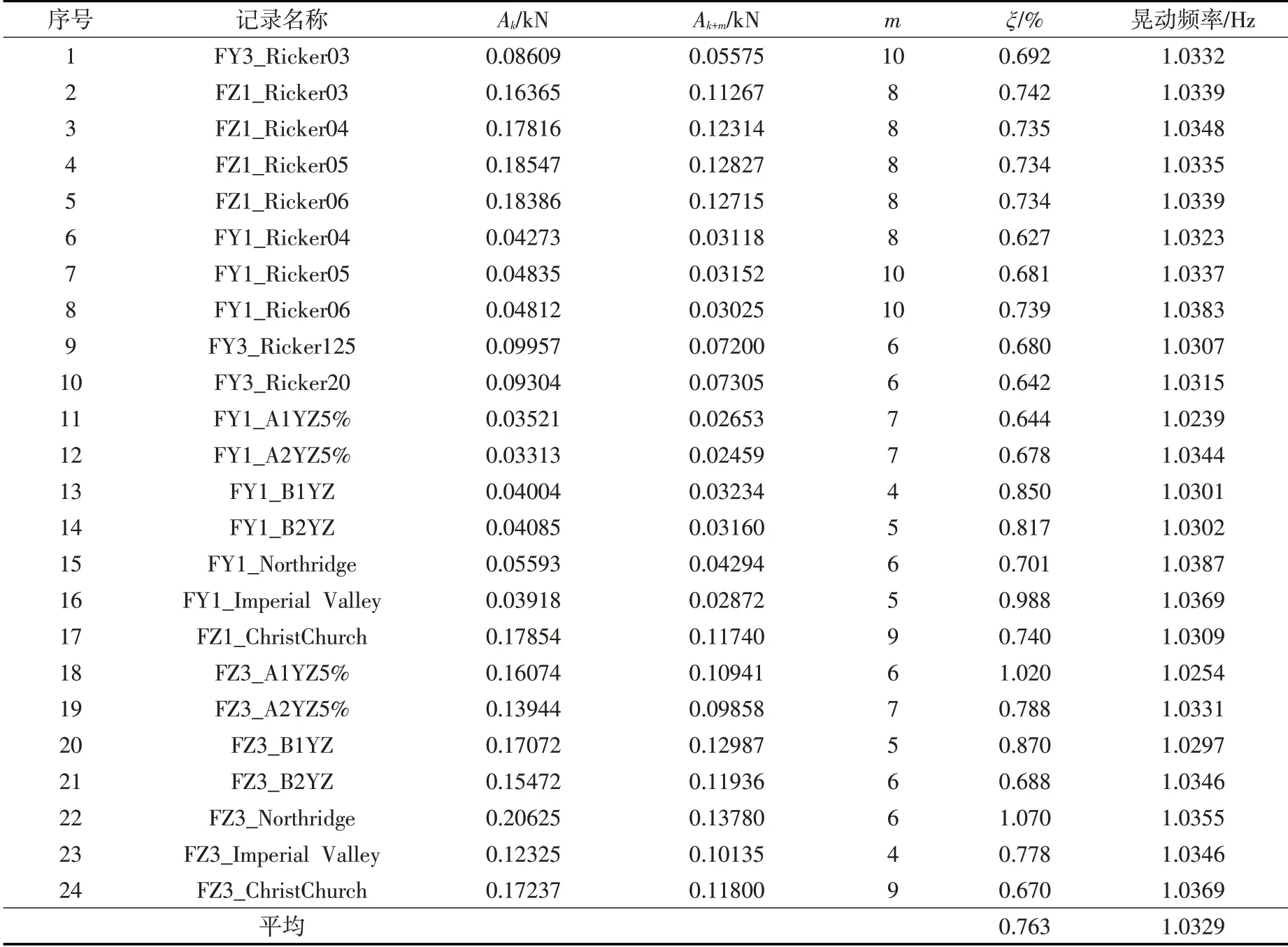
表3 自由衰减曲线计算液面晃动频率和阻尼比结果

对同样刚性矩形容器，Housner基于小幅波动液面为平面假定推导出的容器液面晃动基频为［2］：

同样对刚性容器，李遇春采用位移有限元数值模拟计算的U形渡槽液面晃动频率回归公式为［4］：

式中：R为U形槽底半径；h+R为最大水深。

上述3个公式计算得到的试验渡槽横槽向液面晃动频率也列于表2。矩形容器底宽2l取值与U形槽2R相同。

由于在Housner公式的推导中引入了小幅波动液面为平面假定，等价于增加了液面运动的约束，故得到的晃动基频略高于流体力学方程导出的结果，但差异仅为0.35%。Jaiswal等［16］的试验值也显示Housner公式给出的频率略高。按试验渡槽的水深和槽宽，李遇春的U形槽和矩形槽回归公式［9］给出的频率结果差异很小，表明参与晃动水体主要限于液面附近，U形槽公式的晃动基频略低于矩形槽的结果，体现了槽体形状的影响。但李遇春的结果低于另外两公式，李遇春将原因归于水体的可压缩性影响，但未见具体的分析对比结果。由表2可以看出，依据3种水平白噪声稳态激励响应识别出的液面晃动基频与流体力学方程结果最为接近，但均略小，差异由0.63%至1.14%。原因有两个，一是实际水体液面运动较理论推导的假定复杂得多，另一个是U形槽体形状的影响。特别是实测晃动频率随激励强度下降的趋势，也反映了液面运动非线性的影响。

非常有趣的是依据白噪声稳态激励还识别出了液面晃动的二阶频率（表2），其值与流体力学方程导出的结果非常接近，最大差异仅为0.148%。显然，液面运动的二阶振型较一阶振型对槽内深部形状变化敏感度降低，故U 形槽实测二阶频率值更接近流体力学方程导出的矩形槽二阶频率结果。理论上，矩形槽或U形槽二阶液面振型是关于槽体断面轴线对称振型，槽底部无不平衡水平力出现。但实际试验模型不可能做到绝对对称，基于这很小的不平衡水平力（参见表2）识别出了二阶晃动频率。

由3种水平白噪声激励和非平稳激励后液面自由晃动实测频率逐渐降低的趋势看，液面晃动幅度增加会导致晃动频率的微小下降。

白噪声稳态激励下的液面晃动模态阻尼比一阶为0.64%～0.70%，二阶为0.27%～0.53%，非平稳激励后液面自由晃动对应基频阻尼比约0.76%，较白噪声稳态激励有所增加，同样源于非平稳激励状态液面晃动幅度加大、晃动形态更加复杂。

4 槽内液体对流作用

槽内液面晃动对流作用对渡槽产生的水平力及倾覆力矩是工程设计关注的重点。在Housner的简化等效模型中，水体的对流作用被等效质量和等效弹簧所替代。然而，等效质量与等效弹簧与液面晃动强度无关。等效质量的大小是依据流体液面晃动压力作用于槽壁的动量和槽内液体晃动总动能而确定的。在推导过程中采用了流体液面保持平面的假定。本文振动台试验在渡槽近跨中断面设置了非接触式激光位移计，对渡槽内液面高度变化进行了测量，非接触测量完全避免了对液面运动的干扰。以下将根据试验测试记录的液面晃动波高幅值和水平支座力幅值定量，确定简化等效模型中对应对流作用的等效质量M1。

尽管Housner只给出了矩形槽的简化推导，这里将该方法应用于U形渡槽，如图4所示。图4中水体等效质量M0替代槽内流体的冲击作用，作用高度为h0，对应的U形渡槽动力模型试验结果见文献［13］。等效质量M1和弹簧k1替代槽内水体液面晃动产生的对流作用，作用高度为h1。等效质量M1和弹簧k1系统的振动频率就是上节讨论的液面晃动频率。

假设等效质量M1做正弦运动，位移为D1（t），其作用于槽壁的水平力F1（t）等于质量M1和其加速度之积，而其动能由质量M1和其速度的平方所决定，如以下公式：

图4 U形渡槽流固相互作用简化等效模型

上述运动方程忽略了阻尼项，故液面自由晃动时为一保守系统，其最大动能与最大势能相等。在晃动液面假定为平面的条件下，其最大势能Umax为：

式中：Aw为液面晃动最大波高，参见图4；L为渡槽单跨长度；ρ为水体质量密度。

动能最大幅值与F1（t）幅值之比为：

由式（6）和式（9）即可得到对流作用等效质量M1与水平力幅值F1max和液面最大波高Aw的关系：

由图3可以看到，非平稳激励加振结束后，水平支座力快速进入单频正弦衰减状态，表明除液面基频晃动的对流作用影响外，其它液面高阶晃动对水平支座力影响基本可以忽略不计。然而，从非平稳激励结束后槽内水体液面的波高时程看（图5），尚有复杂非线性晃动持续存在，而非单一频率的正弦波。特别是由式（10）可知，等效质量M1与水平力幅值F1max和最大波高Aw比值的平方成比例关系，因此对二者读值的偏差十分敏感。为了减少波高幅值读取过程中因复杂波形干扰产生的随机误差，波高取值中采用统一的单频正弦衰减函数形式对自由晃动波高时程进行拟合，再从拟合函数曲线上读取对应时刻的波高幅值，用以计算等效质量M1。

图5 渡槽内液面波高时程

依据试验记录的槽内水体自由晃动时对应的支座总水平力幅值、槽壁处波高幅值以及由竖向支座力算出的对渡槽轴线的转动弯矩，计算得到的等效质量M1和作用高度为h1列于表4。表4共计15个加振记录，水平支座力幅值最大392.6 N，最小166.3 N，波高幅值最大37.25 mm，最小16.36 mm，等效质量M1均值为352.6 kg。根据实际模型渡槽端部支座球面铰部位至液面垂直距离0.703 m，计算得到等效质量M1的作用高度h1的均值为0.417 m。

表4 液面晃动对流作用的等效质量M1和作用高度h1

Housner简化等效模型给出的矩形槽等效质量系数和作用高度h1的计算仅与几何形状相关，具体公式如下：

文献［4］采用位移有限元法给出的矩形槽等效质量系数拟合公式以0.511 替代了式（11）中的，约为0.969倍。而其给出的U形渡槽对流作用等效质量系数和作用高度h1的计算公式为：

上述公式中的Mw为槽内水体总质量。

按试验渡槽水深H=0.546 m和槽半宽l=0.35 m算出矩形槽等效质量系数为0.333，等效质量M1为381.8 kg；U形渡槽公式给出的等效质量系数为0.371，等效质量M1为366.9 kg。尽管矩形槽和U形槽的等效质量系数有11%的差异，但等效质量M1的差异仅为4%，这反映了产生对流作用的液面晃动随水深快速衰减的特征。U形渡槽公式给出的等效质量M1较波高与支座力幅值推算均值高约4%。矩形槽和U形渡槽公式给出的作用高度h1分别为0.397和0.416 m，试验数据算出的h1均值与U形渡槽公式给出值仅差0.24%。

由稳态白噪声的水平支座力对台面加速度的传递函数也可对等效质量M1进行定量推测。支座力传递函数的量纲是单位激励加速度下产生的支座力，与质量量纲相同。而假定在液面晃动频率点对应的模态水平支座力均源于等效质量M1的运动，则模态水平支座力为等效质量M1与其模态加速度之积。前面试验得到的液面晃动阻尼比很小，故等效质量M1的模态加速度与台面加速度比为1/2ξ。由此不难得出，等效质量M1为模态水平支座力与2ξ之积。根据3种水平白噪声激励的水平支座力对台面加速度的传递函数和识别出的液面晃动阻尼比表2推算，等效质量M1分别为259.5、288.7和276.6 kg，均值约为275 kg，约为由自由晃动波高得到的78%。数值偏低的原因是晃动频率附近支座力传递函数的频率分辨率仍然不够高，导致模态水平支座力偏小。

上节液面晃动频率及本节的等效质量M1和作用高度h1的试验结果与基于刚性槽假定推导结果的良好一致性表明，对于液面晃动产生的水体-渡槽对流相互作用而言，试验渡槽槽身刚度足够大，视其为槽内水体的刚性边界，完全能够获得精度很高的简化等效模型参数。这一点与水体-渡槽间的冲击作用等效质量对试验渡槽槽身刚度较为敏感的特征明显不同［13］。

根据频率比尺，原型渡槽液面晃动频率约为0.328 Hz。由图3支座力地震响应及图5地震过程中液面波高看，试验对象渡槽液面晃动对流作用对结构地震响应影响占比并不高，这与晃动频率附近地震动能量占比不高一致。尽管试验中并未模拟槽墩结构，但原型渡槽槽墩及槽身结构横槽向自振频率约为1.5 Hz，因此导致液面晃动的地震动能量成分在槽墩顶部基本不会被放大。由此可以判断，对于峰值加速度较高的中、近场地震，渡槽内水体液面晃动的对流作用对渡槽结构地震响应影响有限，而槽内液体的冲击作用是决定渡槽结构地震响应的关键要素。对于长周期能量占比较高的远场大震，地震时可能产生较大液面晃动，使槽内水体对流作用成为决定渡槽结构地震响应的主要因素。需要注意，在分析水体对流作用为主要因素的结构地震响应时，等效质量-弹簧对应的阻尼比与结构阻尼比的取值存在显著差异。

5 结论

本文依托滇中调水工程，采用1/10物理模型通过振动台试验开展大型薄壁输水渡槽流固动力相互作用研究。文中重点分析了稳态白噪声激励和非稳态激励下槽内水体液面晃动对渡槽结构的对流作用，可得如下主要结论；（1）由3种强度稳态白噪声激励响应测得，模型渡槽液面晃动基频分别为1.041、1.037和1.036 Hz，由非稳态激励加震后槽内液面自由衰减晃动测得基频1.033 Hz。晃动频率呈现随晃动幅度减小趋势，但十分接近。试验测试结果与按刚性矩形容器推导的小幅晃动频率公式结果1.048 Hz基本一致，最大差异小于1.5%。由3种强度稳态白噪声激励响应还测得液面晃动二阶频率，与刚性矩形容器小幅晃动频率公式结果更为一致，最大差异小于0.15%；（2）测试得到液面晃动基频对应阻尼比0.72% ～0.83%，均值0.75%，远低于结构地震响应数值分析中常用的5%阻尼比；（3）依据非稳态激励加震后槽内液面自由衰减晃动记录，分析得到U形渡槽模型的Housner简化等效模型中对流作用的等效质量M1和作用高度h1，数值上与刚壁公式结果一致；（4）试验所得液面晃动对流作用的基本参数，频率、等效质量M1和作用高度h1与基于刚性槽假定推导结果的良好一致性表明，对于液面晃动产生的水体对流作用而言，试验渡槽槽身刚度足够大，视其为流体的刚性边界，完全能够获得精度很高的简化等效模型参数。

从渡槽抗震安全设计上看，渡槽液面晃动基频对应的地震动输入能量占比不高，槽墩及槽身结构自振频率高出液面晃动基频数倍，因此，对于峰值加速度较高的中、近场地震，渡槽内水体对流作用对渡槽结构地震响应影响有限，而槽内液体的冲击作用是决定渡槽结构地震响应的关键要素。对于长周期能量占比较高的远场大震，地震时可能产生较大液面晃动，使对流作用成为决定渡槽结构地震响应的主要因素。