面向梯级水库多目标优化调度的进化算法研究

纪昌明，马皓宇，彭 杨

（华北电力大学水利与水电工程学院，北京 102206）

1 研究背景

水库作为一种径流调节的工程手段，在实现水能资源的合理高效利用上发挥着重要作用。随着我国金沙江、雅砻江、澜沧江等流域水库群的相继建成与互联智能电网的有序推进，梯级水库已成为承载多方利益诉求的水资源利用载体，亟需开展多目标优化调度的研究，以有效协调水库防洪、发电、供水、生态等多方面的任务，满足新形势下的调度要求［1-3］。

梯级水库多目标优化调度包括生成备选方案集与方案优选这两部分，首先求解所构建的多目标优化调度模型得到一定数量的非劣解，接着通过理想点法、均变率法等多目标决策方法从中挑选出最佳方案。本文的重点在于第一部分即研究模型的高性能计算方法，以期在给定的计算资源下获得一组高质量的非劣解集供调度人员决策。而水库调度领域目前主要有两种求解方式：通过约束法、权重法等方法将多目标优化转变为单目标优化，再利用传统的数学规划方法求解；通过NSGA-Ⅱ、MOPSO等基于Pareto支配理论的经典多目标进化算法（MOEAs）求解。

多目标转变为单目标求解的方法早期便得到了应用：Foued BA 等［4］应用随机目标规划处理水库群的多目标调度问题，并以突尼斯北部的多库系统为例验证方法的有效性；梅亚东等［5］建立了兼顾发电量与保证出力的黄河上游梯级水电站优化调度模型，采用约束惩罚法将多目标转化为单目标，利用DP-DDDP的组合算法完成求解；武新宇等［6］利用灰色关联度法将多目标优化模型转换成多个单目标优化模型，使用逐步优化算法获得非劣解集；黄草等［7］以长江上游15座大型水库为研究对象，建立包含发电、河道外供水与河道内生态用水等目标的非线性优化调度模型，提出E-POA作为求解算法以提高效率。该方法虽能有效降低多目标优化问题的求解难度，但存在较多的缺点：（1）权重系数等实现问题转变的重要参数只能依据主观经验设置，目前尚无客观合理的取值规则可循；（2）每次求解仅能得到一个调度方案，且因问题Pareto前沿的形状未知，多次计算可能无法获得等计算次数规模的非劣解集，即无法保证能为决策者提供一定规模的备选方案集；（3）非线性规划、动态规划等传统单目标算法在处理大规模水电调度问题上存在严重的“维数灾”问题。

上述缺点导致该方法的使用受到限制，许多学者开始利用经典MOEAs：Chang L C 等［8］构建最小化各库供水短缺指数的台湾翡翠与石门水库的优化调度模型，通过NSGA-Ⅱ算法进行研究；覃晖等［9］建立三峡梯级水电站的中长期发电优化调度模型，提出SPDE算法完成求解；Ahmadi M等［10］利用NSGA-Ⅱ算法研究Karoon4水电站的多目标发电优化调度，并提取其最优运行规则；Luo J等［11］考虑安康水库防洪与供水两方面目标，提出一种基于偏好选择的多目标免疫算法MOIA-PS 求解模型；王丽萍等［12］建立溪洛渡-向家坝梯级水库多目标优化调度模型，采用NSGA-Ⅱ算法获取非劣解集，接着引入结构方程模型定量分析各目标间的互馈关系。该方法计算效率较高，单次求解即可得到一组调度方案，且对问题的目标函数与约束条件的形式不作要求，但缺陷在于经典MOEAs的算法性能通常随决策空间或目标空间维数的增长而下降，随着水库群规模的不断扩大与调度管理要求的不断提升，梯级水库多目标优化调度本质上已属于大规模高维多目标优化问题，其复杂性是经典算法所难以解决的。

如何处理多目标优化调度的高维特性已成为计算关键，而水库调度领域尚未针对此提出或引入相应的优化策略或算法，故本文以多目标粒子群算法为基础，采用超体积指标保证高维目标空间下算法的选择压力，采用问题变换策略保证高维决策空间下算法的搜索力度，提出LMPSO（Large-scale Many-objective Particle Swarm Optimization）算法，通过溪洛渡-向家坝梯级水库的实例研究，验证所提方法在梯级水库多目标优化调度这一实际工程问题中的应用效果。

2 梯级水库多目标优化调度模型

本文以金沙江下游最末梯级的溪洛渡-向家坝为研究对象，考虑发电、河道外供水与河道内生态用水这三方面目标，构建溪洛渡-向家坝梯级水库发电-供水-生态的多目标优化调度模型。

2.1 目标函数

（1）发电目标：调度期内的发电量f1、发电保证率f2与弃水量f3。

式中：t和i分别为时段编号与水库水电站编号；T和n分别为调度期时段总数与水库水电站总数；Ni，t为i电站t时段的平均出力，kW；Δt为单位时段长度，h或s；表示t时段系统出力Nt是否满足保证出力，1表示满足，0表示不满足；为i库t时段的平均弃水流量，m3/s。

（2）供水目标：调度期内的供水缺水量f4、供水保证率f5与供水最长破坏历时f6。

（3）生态目标：调度期内的生态缺水量f7、生态保证率f8与生态最长破坏历时f9。

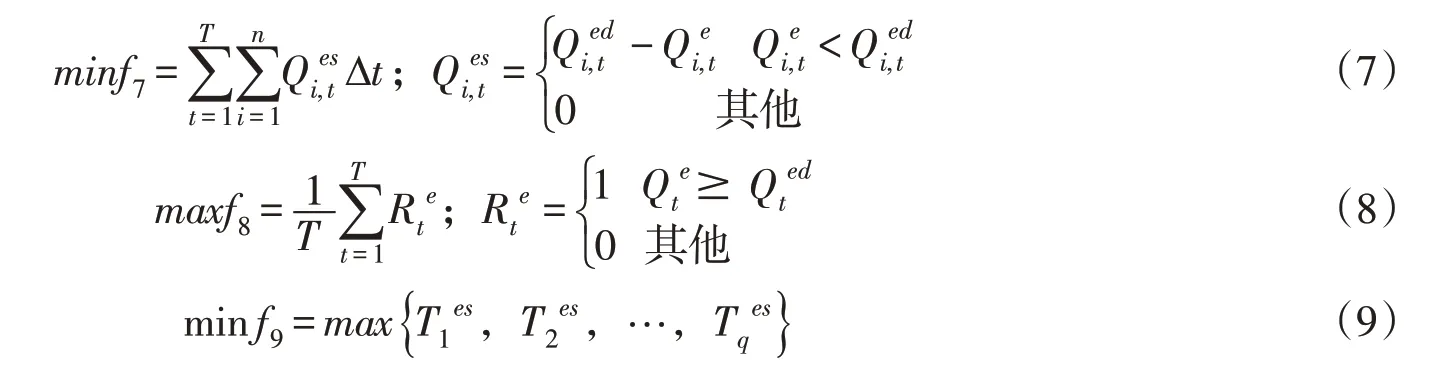
2.2 约束条件

（1）水量平衡约束：

式中：Vi，t和Vi，t+1为i库t时段的时段初末库容，亿m3；Qi-1,t、Qi,t和分别为（i-1）库t时段的平均出库流量和i库t时段的平均出入库流量，m3/s。

（2）水位约束：

式中：Zi，t为i库t时段初水位；和为i库t时段初的水位上下限，m。

（3）流量约束：

（4）出力约束：

（5）边界约束：

式中：Zi,start和Zi,end为i库给定的调度期初末水位，m。

3 求解算法

3.1 基于超体积指标处理高维目标空间高维多目标优化问题（MaOPs）一般指目标个数大于5 的多目标优化问题（MOPs）［13］，经典MOEAs多用于处理2 ～3维目标的MOPs，由于以下两方面的原因难以解决MaOPs：（1）高维目标空间下算法的收敛压力丧失。此时种群中大部分个体之间相互非支配，导致基于非支配排序的选择策略失效，算法的选择进程被多样性指标所支配；（2）高维目标空间下结果的多样性难以保证。种群个体在高维目标空间内分布稀疏，导致基于目标空间内欧氏距离的多样性维持策略失效。为解决上述问题学者们提出了一系列方法，大致可分为4类［14-19］：直接修改传统Pareto支配的定义；采用算法的性能评价指标作为选择标准；基于分解思想将原问题分解为一组简单的子问题；删除冗余或不相关的目标以实现维度缩减。本文选择第2类处理方法，将超体积指标作为个体适应值引导算法的交配选择与环境选择。

超体积指标（hypervolume）由Zitzler E 等［20-21］提出并用于定量比较不同MOEAs 的性能，是目前最为通用的集合质量度量标准之一。该指标具有优秀的数学性质，是已知的唯一与Pareto支配严格单调的一元指标［22-23］，且不同于GD、IGD等指标，其可在Pareto前沿未知的情况下同时评价解集的收敛性与多样性，故可应用于实际的科研与工程问题中。超体积指标IH定义如下：

式中：A为决策空间内的待评价集合；r为目标空间内的参考点；λ为勒贝格测度；H（A，r）表示目标空间Z内被A对应的目标向量集f（A）与r所包围的区域。

IH以单个标量值衡量整个集合的质量，而选择操作要求指标的评价对象是集合中的单个个体，故需对该指标进行修改。此处使用修改后的超体积指标，将移除集合中某一个体所造成的超体积损失值作为评判该个体优劣的标准，其定义如下［24］：

式中：k为待移除个体的总数；表示目标空间内被a和A中其它任意（i-1）个个体所共同且唯一弱支配的区域。

（1）准备阶段：首先输入估算所需参数：集合A、参考点r、参数k以及取样规模M；接着构建包含所有Hi（a，A，r）的样本空间S，为方便体积计算与样本点生成，令S为包含所有Hi（a，A，r）的边长轴平行的最小超立方体；最后完成参数ai的计算与适应值vi的初始化。

（2）取样阶段：首先均匀随机生成样本点sj∈S，j=1，…，M；接着针对每一个样本点sj，检查其是否位于任何满足1≤i≤k且a∈A的Hi（a，A，r）区域内，检测方法为获取A内所有弱支配sj的个体组成的集合UP，若其基数满足1≤|UP|≤k，则sj位于所有满足i=|UP|且a∈UP的Hi（a，A，r）内，更新A中相应个体的适应值；最后即可获得集合A中个体的适应值。

3.2 基于问题变换处理高维决策空间影响优化问题复杂性与求解难度的一个重要因素是决策变量的维数，大规模多目标优化问题（Large-scale MOPs）通常指维数在200以上的多目标优化问题［27］，大多数多目标算法在30维以下的问题上表现良好而无力解决高维问题，主要原因在于：为使搜索能覆盖整个决策空间，种群的规模应随决策变量维数的增长而扩大，即实现高维决策空间内的有效搜索需要大规模种群集合，而实际设计中为保证计算效率，学者们一般将种群规模限制在10 ～1000的范围内，致使高维情况下无法搜寻至决策空间内的部分区域，导致所得结果往往并不理想。为解决该难题目前倾向于使用一种名为协同进化（cooperative coevolution，CC）的机制，其由Potter和De Jong［28］提出并成功应用于求解大规模优化问题。CC基于分解思想，按一定的划分原则将问题的高维决策向量分解为一组低维决策子向量，由多个相互独立的种群同时优化向量的不同部分，并在规定阶段进行重组以开展整体优化，由此将复杂的高维优化问题转化为一组简单的低维子问题，通过多种群协同优化的方式完成求解。

然而协同进化并不适用于梯级水库多目标优化调度，其原因在于该问题的约束条件复杂繁多，通常包括调度期内各时段初末的水位约束与各时段内的平均流量、出力约束，无论是以各库各时段初的水位为决策变量，还是以各库各时段内的平均出库流量为决策变量，都必须将其作为一个整体进行优化，以保证优化过程中个体的可行性，避免算法在不可行域内的无效搜索。为此本文引入问题变换策略［29］，在整体优化的前提下实现搜索空间的降维，以期有效降低问题的求解难度。

首先介绍问题变换的相关概念。令Z为n维决策向量与m维目标向量的多目标优化问题，其数学表达式如下：

图1 基于蒙特卡洛法的指标估算流程图

对于任意决策向量x′，可通过变换函数ψ与权重向量w将其转化为另一决策向量x，数学表达式如下：

在ψ内参数x′给定的情况下，改变w的值即可获得不同的决策向量x，由此将Z转换为新的问题Zx′，将待优化对象由决策向量x转变为权重向量w：

转换后搜索空间的维数依然为n，为实现降维进行变量分组，与CC不同各组变量并未实行相互独立的优化：将n维决策变量划分为γ组{g1，…，gγ}，接着修改权重变量与决策变量间的对应关系，由一一对应改为一个权重变量与一组决策变量相对应，由此将待优化的权重向量w由n维降至γ维。通过上述方法将n维决策空间的多目标优化问题Z变换为γ维的问题Zx′，再利用MOEAs 进行求解，即可在降维后的子空间内更快更彻底地搜索优秀个体。然而该方法有一明显缺点，被划分至同一组中的决策变量，当相应权重变量的值改变时其值将一同改变，即同一组变量的值无法相互独立地变化，这将较大程度地限制算法在原决策空间内的可搜索区域。

3.3 LMPSO算法本文选择以速度限制策略为特征，在低维MOPs上表现优异的多目标粒子群算法SMPSO［30］为基础，以3.1节的超体积指标I h k取代拥挤距离这一传统的多样性指标，以3.2节的问题变换作为实现搜索空间降维的手段，由此提出一种能有效处理梯级水库多目标优化调度这一大规模高维多目标优化问题的进化算法LMPSO。首先对改进策略的应用细节进行说明：

（2）问题变换降低搜索空间维数。算法求解原问题理论上能探索整个决策空间，但在高维情况下的收敛速度可能非常慢，致使给定迭代次数下所得结果的收敛性较差，而问题变换策略能在决策向量整体优化下实现搜索空间的降维，使算法能更深入地挖掘较小空间内的优化信息，进而提高收敛速度，但缺点正如3.2节末尾所述，其限制了决策空间内的搜索范围，不利于维护多样性，因而降低了算法近似整个Pareto前沿的能力。为此采取原问题与变换后问题交替优化的形式，以兼顾结果的收敛性与多样性，并在变换后问题的优化阶段，从存档中选取不同个体的决策向量作为变换函数ψ的参数x′，以探索决策空间内的不同区域。

接着给出LMPSO的算法流程图，如图2所示。

最后对图2中的重要操作，即优化操作Optimise和更新操作Update进行说明。

优化操作记为Optimise（Z，Pop，t），输入参数分别为待优化问题Z、初始种群Pop和最大函数评价次数t，该操作的流程如图3所示，具体步骤为：

（1）初始化个体历史最优集合Pbest与种群历史最优集合Gbest。Pbest用于记录种群Pop中每个个体所经历过的最优位置，将其初始化为Pop；Gbest的初始化则较为复杂，首先将Pop内位于第一非支配层的个体添加至Gbest，接着检查|Gbest|是否超过给定值size，若是则基于适应值迭代删除较差个体，最后计算Gbest内各个成员的适应值I|Gbest|h作为交配选择的依据。

图2 LMPSO算法流程图

（2）更新种群Pop，再利用Pop更新Gbest与Pbest，重复此操作直至函数评价次数达到t。首先针对种群中的每个个体，从Gbest中基于I|Gbest|h选取优秀个体作为粒子速度更新的参数gbest，从Pbest中选取对应编号的个体作为参数pbest，以此计算个体的速度与位置，有必须满足的硬性约束则需检查并修正决策向量；接着利用新生成的Pop，将其与Gbest混合并对混合集合执行如Gbest初始化般的操作以更新Gbest，将其与Pbest内的个体一一比较以更新Pbest。

更新操作记为Pop=Update（Gbest，W_Gbest1，…，W_Gbestq），输入参数分别为原问题Z的优化成果Gbest和变换后问题Zx′的q次优化成果{W_Gbestk}k=1，···，q，该操作的流程如图4所示，具体步骤为首先清空给定规模size的种群集合Pop，接着从所有存档的混合集合mixedGbest中挑选优秀个体加入Pop，按|mixedGbest|分为三种情况：

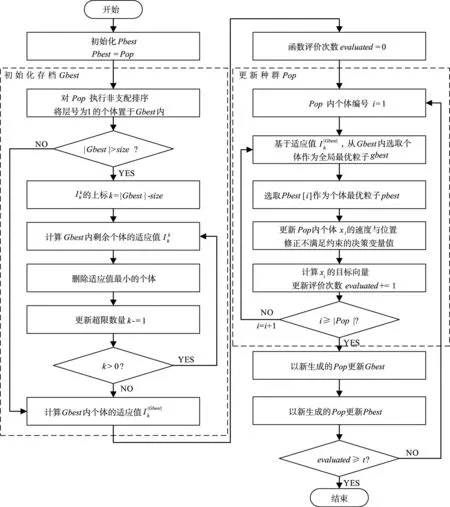
图3 Optimise操作流程图

（1）|mixedGbest|＜size。此时为满足Pop的规模要求，对mixedGbest集合执行交叉变异操作，生成（size-|mixedGbest|）个新个体以填充集合，令Pop=mixedGbest。

（2）|mixedGbest|=size。令Pop=mixedGbest即可。

（3）|mixedGbest|＞size。此时对mixedGbest集合执行非支配排序，从第1层开始将各层个体依次移入Pop直至|Pop|≥size，若|Pop|＞size，则基于迭代删除最后加入的层中（|Pop|-size）个个体。

4 实例分析

金沙江作为长江上游河段，起于青海省、四川省交界处的玉树州直门达，止于四川省宜宾市东北翠屏区合江门的长江干流河段，全长3481 km，流域面积为50.2万km2，流域地形呈北高南低。溪洛渡-向家坝梯级水库位于金沙江的下游干流，作为开发与利用金沙江水能资源的骨干工程，该系统以发电为主，兼有防洪、拦沙、供水、生态等任务，其参数与拓扑图如表1与图5所示。

本文以溪洛渡-向家坝梯级水库为研究实例，以2.1节中的发电、供水和生态这三方面的指标最优为目标，建立梯级水库多目标优化调度模型，并利用LMPSO算法完成求解。为验证所提算法的有效性，将计算结果与4 种具有代表性的MOEAs 进行比较，即NSGA-Ⅱ、SMPSO、NSGA-Ⅲ及KnEA，且为测试各算法在不同维度的决策空间与目标空间上的表现，分别以2010—2012年和2007—2012年为调度期，以月和旬为调度时段，在来水已知条件下，分别以（f1，f4，f7）、（f1，f2，f4，f5，f7，f8）和（f1，…，f9）为目标，构建12种维度组合的多目标优化调度问题Zi，j，其中i为决策向量的维数，，j为目标向量的维数，j∈{3，6，9}。

图4 Update操作流程图

表1 梯级水库特征参数

4.1 参数设置首先选取决策变量并决定约束条件和目标函数的处理方式。为有效处理水量平衡、调度期初末水位限制等约束，将调度期内各库各时段初的水位作为决策变量以实现编码；为满足调度中的硬性约束，在计算前依据水位、流量、出力等约束条件构建整个调度期梯级水库的水位约束廊道，在计算中通过水库当前阶段的水位值确定下一阶段水位的可行范围；由于算法涉及目标空间内的欧式距离计算，故需对各维目标实现无量纲化，将其均转化为越小越优型。

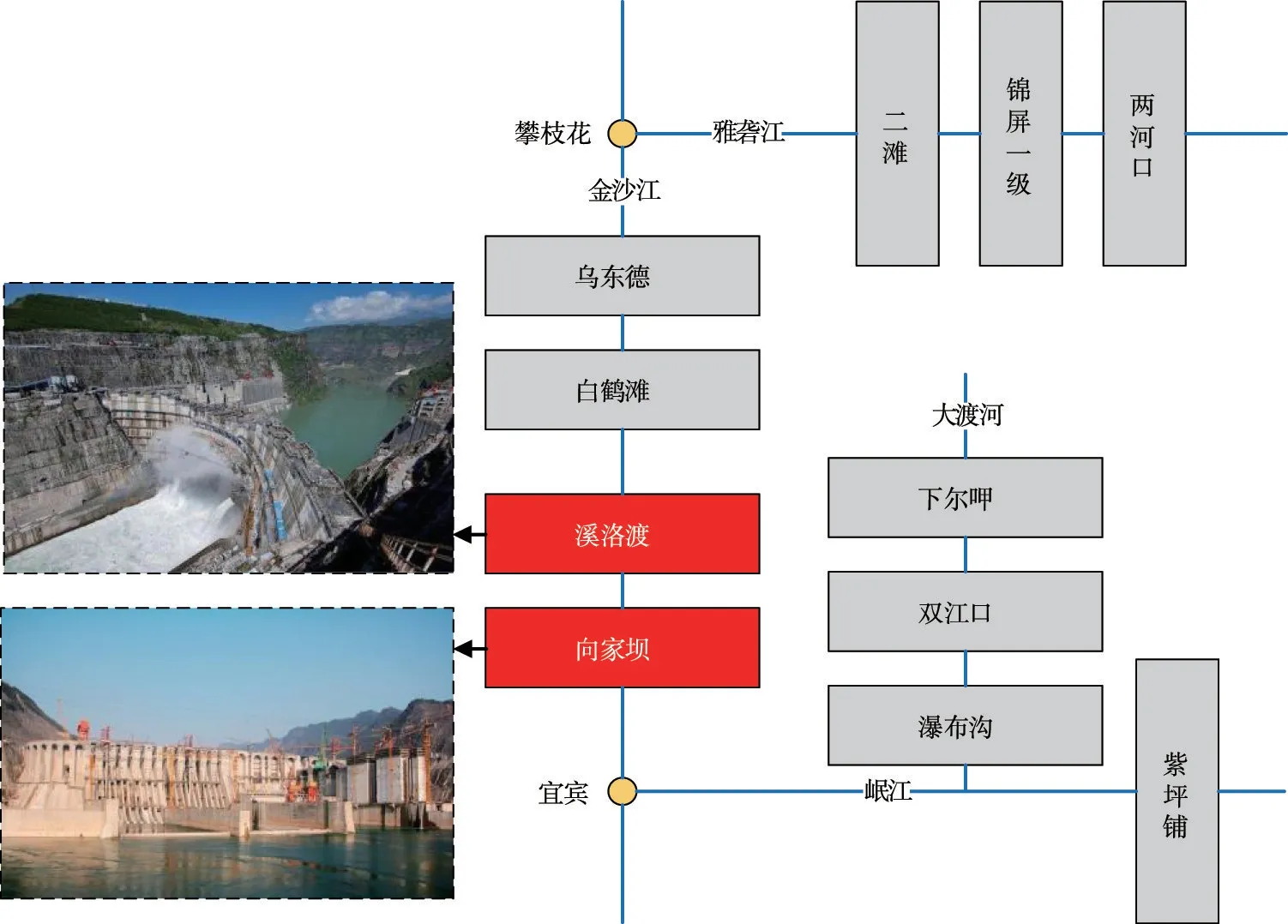
图5 梯级水库拓扑图

接着进行算法的参数设置，分为通用参数与特有参数。通用参数设为：每个算法在每个问题上独立运行30次，每次运行的种群与存档的规模均取100，每次运行的最大函数评价次数取105。特有参数设为：4种对比算法的特有参数均参考原文献进行设置；LMPSO 中，为估算超体积指标将取样规模设为104，为实现问题变换将分组策略、分组规模与变换函数分别设为线性分组、12与区间交集变换，算法单次运行的每轮迭代中，当优化原问题时令最大函数评价次数为103，当优化变换后问题时令决策向量的选取规模为目标向量维数，种群与存档规模均为50，最大函数评价次数为500。

最后选择算法的性能评价指标。本文以超体积指标IH综合评价所得解集的收敛性与多样性，且为检验不同算法的指标值之间是否存在显著差异，使用显著性水平a=0.01的Mann-Whitney U检验。

4.2 结果分析通过比较5种算法在12个维度组合的多目标优化调度问题Zi，j上所取得的IH值，以评价各算法处理该类问题的性能，其实验结果如表2所示。表中第2 ～6列括号外的数字为对应列算法在对应行问题上所测得的IH指标中位数的相对值，该值是对应列算法在对应行问题上独立运行30次所统计的结果，不同算法在同一问题上的最优值以粗体标记，表现过差的算法其值以破折号标记。第2 ～6列括号内的数字为对应列算法在对应行问题上的得分，该值表示参与求解的方法中表现显著优于对应列算法的数量。

表2 不同算法的结果对比

首先分析不同维度的问题上各个算法的表现。当变量维数i与目标维数j较小时，SMPSO能取得高质量的非支配解集，其在Z72，3上的指标值与最佳的KnEA无显著差距，在Z144，3和Z216，3上均取得最优的IH值，由此验证了SMPSO在解决低维问题上的优秀性能。当目标维数j增加时，SMPSO的表现随之恶化，原因在于该算法并未针对高维目标空间设计相应的策略，而NSGA-Ⅲ和KnEA 的表现则较低维情况有明显提升，且NSGA-Ⅲ在Z72，9上取得最优值，KnEA在Z72，6和Z144，6上的表现与最佳的LMPSO无显著差距，原因在于NSGA-Ⅲ和KnEA是专门用于处理MaOPs的方法，NSGA-Ⅲ采用了基于参考点的多样性维护策略，KnEA则提出在选择操作中优先考虑拐点，两者在处理变量维数较低的高维多目标优化问题上表现较好。当变量维数i也增加时，即可观察到LMPSO 较其它算法的显著优势，在Z216，6、Z216，9、Z432，6与Z432，9这4 个大规模高维多目标优化问题（i＞200 且j＞5）上，LMPSO均获得最佳指标值，且在最高维数的Z432，9上其值明显高于其它算法，这归功于LMPSO不仅利用超体积指标来指导算法的选择操作，以保证高维目标空间下的收敛压力与集合多样性，而且采用问题变换策略对搜索空间进行降维，以确保高维决策空间内信息的高效挖掘。NSGA-Ⅱ这一经典算法在除Z72，3的其它问题上表现均不理想，尤其在高维问题上其值常接近0。

接着评价各个算法在该类问题上的总体表现。本文所提出的LMPSO在12个问题上取得了8个最优的IH值，在Z216，3和Z72，9上的指标值与最优值无显著差异，由此体现出LMPSO较其它方法的竞争力，SMPSO 在Z144，3和Z216，3这两个问题上取得最优值，NSGA-Ⅲ和KnEA 则分别在Z72，9与Z72，3上取得最好的结果。对表2中不同算法括号内的分数进行累加可得，LMPSO取得最佳的总分数3，接着是KnEA其分数为12，SMPSO与NSGA-Ⅲ的分数非常接近，分别为24和25，NSGA-Ⅱ则取得最差的分数43。由此表明在超体积指标IH评价非支配解集质量的条件下，LMPSO在处理多目标优化调度问题上的总体表现显著优于其它4种对等比较的方法，其解集质量具有明显的优势，故更适合作为梯级水库多目标优化调度的求解方法。

5 结论

梯级水库多目标优化调度这一问题的高维特性日益凸显，如何实现有效处理已成为水库调度领域的研究热点与难点。本文提出以多目标粒子群算法为基础框架的LMPSO算法，针对所优化问题的高维特征，利用超体积指标作为适应值以指导算法的交配选择与环境选择，通过问题变换策略充分挖掘决策空间内的优化信息。最终以溪洛渡-向家坝梯级水库为研究实例，将4种多目标进化算法与LMPSO进行比较分析，实验结果表明：LMPSO算法的总体表现较对比算法有明显提升，且在高维情况下其性能优势更为显著，故更适合应用于当前形势下的梯级水库多目标优化调度中。下一步的工作将着力于研究LMPSO算法在其它类型的水资源多目标优化调度上的使用效果。