火星车系统动力学建模与仿真分析

潘 冬，李德伦，袁宝峰，贾 阳，王 瑞，张泽洲

（北京空间飞行器总体设计部，北京 100094）

引 言

星球车是当前世界各国开展地外星表探测的重要手段。俄罗斯月球车“Lunokhod1”“Lunokhod2”于1970年和1973年相继成功登陆月球，标志着星球车进入实际应用阶段[1]。1971年7月30日，由“阿波罗15号”（Apollo 15）携带的美国载人月球车（Lunar Roving Vehicle，LRV）登陆月球，成为世界上最早实现空间应用的载人星球车。l971年，俄罗斯火星车PROP-M随苏联自动考察站“火星3号”（Mars-3）探测器登上火星，是世界上第一辆用于火星探测的星球车[2-3]。1997—2004年，美国掀起应用星球车进行火星探测的热潮，先后成功发射了“旅居者号”（Sojourner）、“勇气号”（Spirit）和“机遇号”（Opportunity）火星车。2012年，美国“好奇号”（Curiosity）成功着陆火星，成为目前功能最为强大的火星车[4-5]。2013年，中国“玉兔号”月球车成功登月，标志着中国成功掌握了基于星球车的星表探测技术[6]。2016年，中国首次火星探测任务正式立项，计划于2020年发射火星探测器，一次实现“环绕、着陆、巡视”3个目标。

根据美国的火星探测经验：六轮被动摇臂-转向架式火星车在火星表面行驶时多次发生车轮沉陷，且爬坡能力不佳[7]。针对此问题，中国火星车采用六轮主动悬架式移动系统，通过悬架的主动变形，不仅可以实现车体高度调整、抬轮、蠕动前行等，还可改变系统质心的相对位置，对于改善火星车的通过性能以及稳定性具有重要意义。

主动悬架式移动系统属于首次在轨应用，国内外学者对其研究相对较少，邓宗全等[8]对主动悬架式移动系统抬轮原理进行了分析与验证；陶灼等[9]对火星车主动悬架的几何参数进行了分析优化；郑军强[10]对主动悬架式移动系统设计及蠕动策略开展了研究；唐玲等[11]对主动悬架式火星车稳定裕度优化策略进行了研究。也有较多学者对星球车动力学特性进行研究，重点研究星球车车轮与星壤之间的轮地特性，丁亮[12]对月/星球车轮地作用地面力学模型开展了深入研究，杜建军[13]对非对称行星探测车行走系统进行了动力学仿真与运动性能分析。而对于主动悬架式火星车移动性能以及动态特性的研究较少。

火星表面环境复杂，移动系统需能够在火面非结构化复杂环境中实现远距离行驶，安全到达指定位置，并保障自身的安全和稳定工作，这就要求系统具有良好的通过性能。本文以中国主动悬架式火星车为对象，结合系统特点建立其动力学模型，通过仿真分析对火星车行走性能以及不同地形下车体升降、车轮故障后抬轮行走等能力开展研究，为火星车后续在轨应用以及制定故障处置策略提供参考。

1 移动系统组成

中国火星车依旧采用六轮驱动主副摇臂悬架形式，但是改进为主动悬架形式（见图1），相较被动悬架增加了夹角调整机构和离合器机构。移动系统机构主要包括6套车轮驱动机构、6套车轮转向机构、2套夹角调整机构、2套离合器机构和1套差动机构，以及由2套主摇臂、2套副摇臂、6套转向臂组成的悬架结构。17套机构中除差动机构为被动机构，其余16套机构均为主动机构，通过直流无刷电机和旋变实现机构的速度或位置闭环控制。

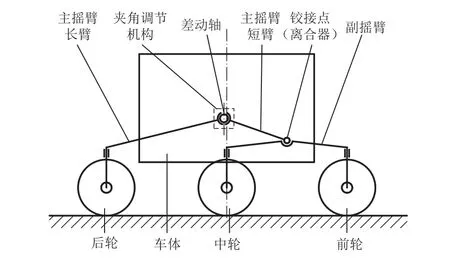
图1 主动悬架简图Fig. 1 Diagram of active suspension

每个车轮处分别配置1套驱动机构和1套转向机构，主摇臂长臂和主摇臂短臂间安装夹角调整机构，可通过夹角调整机构运动改变主摇臂长臂和短臂间夹角，进而改变车体高度；主、副摇臂相互铰接，铰接点处安装离合器机构，通过离合器打开、闭合实现主副摇臂间自由度的释放和锁死。正常情况下离合器为打开状态，以保证主副摇臂间可根据地形自由转动，确保6个车轮均可与地面接触，而当车轮发生故障后，故障车轮侧离合器将主副摇臂锁死，通过控制夹角调整机构特定运动可将故障车轮抬起，并通过其余车轮继续进行移动探测，从而提升火星车的故障容错能力和寿命。

中国火星车的步态可以分为：普通步态、蟹行步态、车体升降、蠕动步态、抬轮行走。其中普通步态与被动悬架式星球车功能基本相同，为火星车常规使用的步态，但通过六轮独立转向可实现蟹行运动功能，用于灵活避障及大角度爬坡等使用环境。其余为主动步态，在特殊场合下使用，包括落火后车体抬升，车轮沉陷后蠕动脱困，车体着地的抬轮脱困，故障轮抬离地面等应用场景，这使火星车的悬架功能更加强大，也更加复杂。

采用主动悬架使得火星车具有如下优点（主动悬架和被动悬架比较示意图见图2）：

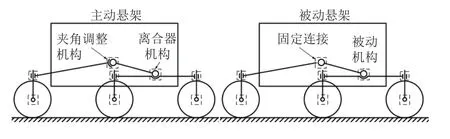
图2 主动悬架和被动悬架比较示意图Fig. 2 Comparison between active and passive suspension

1）车厢高度可调整，能节省发射过程中的支撑结构，着陆后通过车体高度抬升至常态高度，并从着陆平台驶离；

2）具备轮步行走（蠕动）功能，增强车轮沉陷脱困能力；

3）可改变车体质心位置，或抬起车轮，减少沉陷车轮的轮压；

4）可改变车体质心高度，从而减小爬坡时前后车轮的载荷和车轮驱动力矩的差异，提高火星车爬坡能力；

5）车轮故障时，可抬起故障车轮，1个车轮故障可通过5轮行走，两侧各1个车轮故障，可通过4轮行走。

2 移动系统动力学建模

依据上节中火星车移动系统构成机理，应用ADAMS软件建立火星车系统动力学模型，火星车多柔体动力学模型由39个零部件（含地面）组成，各部件的拓扑关系如图3所示。

火星车行走过程中，由于地形起伏变化，移动系统摇臂结构不仅承受火星车的静态载荷，还将承受由颠簸地形引起的交变动态载荷，因此建模过程中考虑各摇臂结构柔性影响，通过假设模态法建立摇臂的柔性体模型，摇臂结构主要承受弯曲载荷，建模时各摇臂杆件相应基频如表1所示。

由于火星车移动系统关节存在齿轮啮合、轴承支承和大量螺栓连接，结构刚度较低，采用BUSHING单元定义其6个方向的连接刚度和阻尼。整车共建立14个柔性连接，分别位于6个车轮驱动关节、转向关节，2个夹角调整机构连接处。据分析及部分实测结果，仿真分析中假定各连接处刚度和阻尼系数：拉压刚度系数为100 N/mm、扭转刚度系数为1×106N·mm/（°）、拉压阻尼系数为1 000N·s/mm、扭转阻尼系数为1 000 Nmm·s/（°）。

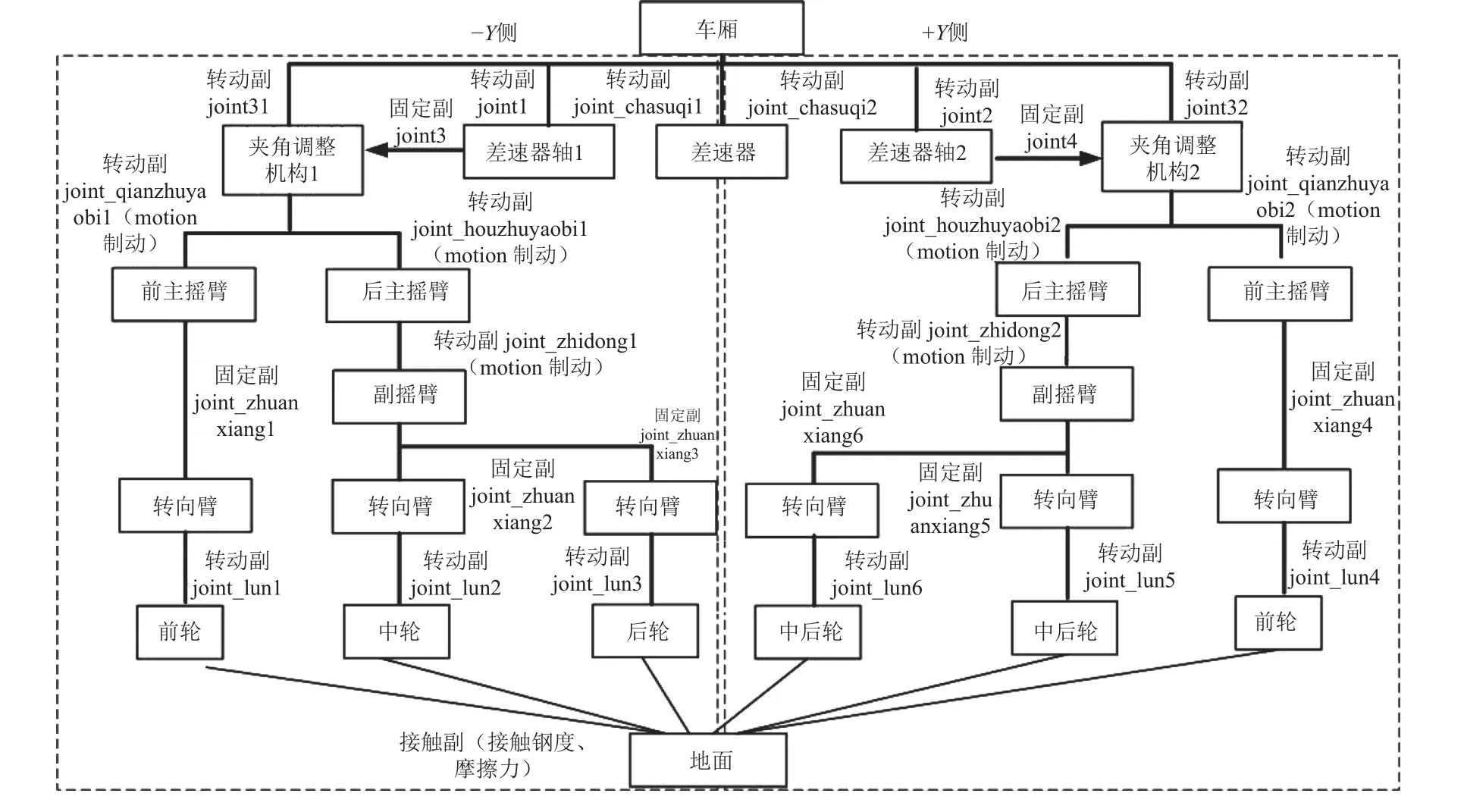
图3 火星车移动拓扑关系Fig. 3 Mars mobile system topology

表1 柔性件模态Table 1 Flexible part mode

火星车车轮为带翅片的鼓形轮结构，最大外径为300 mm，宽度200 mm，外圆分布20个高为5 mm的轮齿。本文重点研究火星车移动装置承载及不同运动步态下的受力及动态性能，对车轮与地 面间的轮土作用模型进行简化，模型中车轮-地面接触采用库伦-摩擦模型来等效车轮与地面间的相互作用，仿真分析中火星车车轮与地面接触刚度假定为100 N/mm，摩擦系数为1.2。

建立火星车本体坐标系为参考坐标系，原点O为结构底板对火面的理论几何中心；Z轴位于结构底板对火面内，+Z轴指向前进方向；X轴沿结构底板对火面法线方向，+X轴背向火星表面；Y轴与X轴和Z轴构成右手坐标系。

火星车系统动力学模型如图4所示。模型中所用参数为：火星车系统质量为250 kg，质心位置（400 mm，0 mm，50 mm），重力加速度为3.72 m/s2，标称状态（车厢底面距地高度300 mm）下，轮间距为775 mm，主摇臂长臂810 mm，主摇臂短臂390 mm，主副摇臂铰接点距地高度为350 mm，主副摇臂铰接点与中后轮中心距离为430 mm，差动轴距车厢底面距离为50 mm。

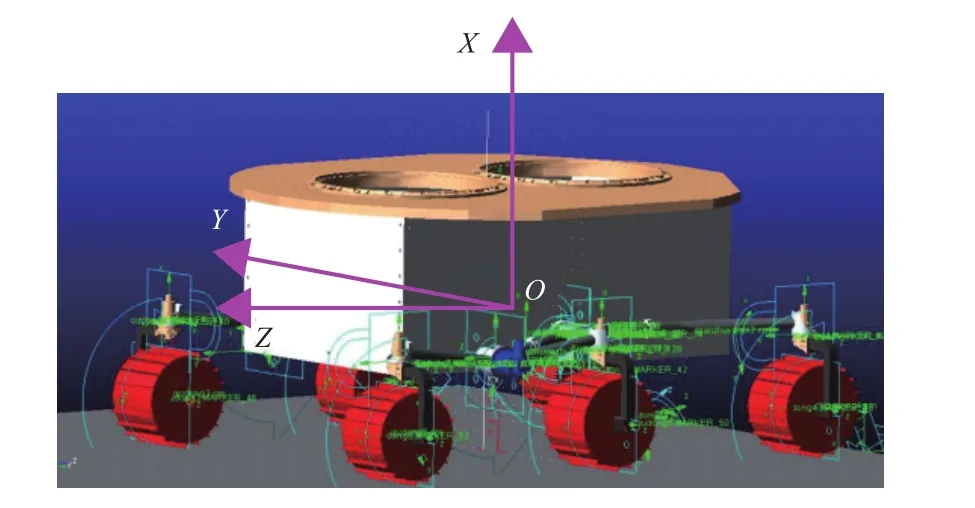
图4 火星车动力学模型样机Fig. 4 Dynamic model prototype of Mars rover

3 火星车典型步态性能仿真分析

3.1 普通步态能力分析

火星车普通步态主要指直线行走与行进间转向，火星表面普通步态行走典型工况包括水平地面行走、前向爬坡行走（假定坡度为20°）、后向爬坡行走以及越障行走（凸起障碍与凹陷障碍），此种步态下重点关注车轮所受法向力以及驱动力，进而考核火星车的能力裕度。

通过建立的火星车系统动力学模型分别对上述工况进行仿真分析，并提取各状态下车轮所受最大法向力及所需最大驱动力矩，车轮所受法向力如表2所示。

水平地面行驶时，地面对前轮、中轮和后轮的法向力相近；前向爬坡时后轮法向力最大，后向爬坡时前轮法向力最大。越障和过坑时车轮法向力明显增加，中轮较前后轮增加50%～100%。通过结果分析可知，火星车构型设计合理，水平地面各轮载荷分配均匀，而当爬坡时，受重力分配影响，位于下坡的车轮承载大，为了提升火星车爬坡能力，爬坡时可通过主动悬架降低车体质心高度，并且由于车体质心位于中轮正上方，越障过程中中轮承受法向力更大，设计车轮时需重点考虑。

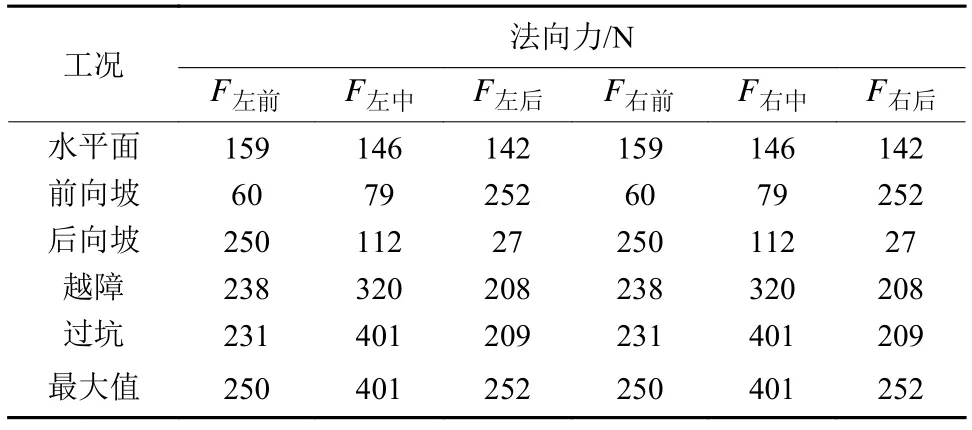
表2 车轮法向力Table 2 Normal force of wheel

普通步态行走时，垂直越障、过坑工况对车轮驱动力需求较大。设计车轮时，前后轮驱动力矩应不小于40 Nm，中轮驱动力矩应不小于59 Nm。车轮所需最大驱动力矩如表3所示。

表3 车轮驱动力矩Table 3 Drive force of wheel

火星车行进转向时，火星车包络几何中心运动轨迹距转向中心的最大距离与最小距离之差是体现转向精度重要指标，图5为以2 m半径转向时火星车几何中心在YZ平台内坐标轨迹，从图中可看出位置曲线圆滑，且运动360°后轨迹闭合，最大距离与最小距离之差小于的100 mm，转向半径精度优于5%。

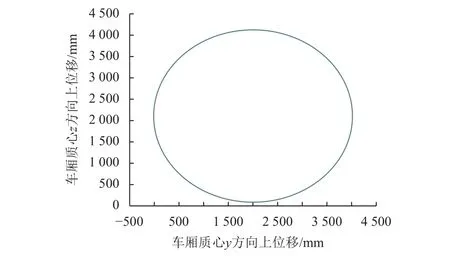
图5 2 m半径行进间转向-车厢YZ位置Fig. 5 Steering position during travel

3.2 地形条件对车体高度调整影响分析

通过主动悬架对火星车车体高度进行调整是移动系统关键功能，通过车体高度调整功能可实现：火星车由压紧状态（车体高度0 mm）调整至标称运动状态（车体高度300 mm）；提高车厢底面离地高度提升火星车通过性能；降低车厢底面离地高度提升火星车爬坡能力。本部分分别对水平地面、正向坡、反向坡等不同地形条件下车体升降过程进行动力学仿真分析，一方面仿真验证移动系统车体升降性能，另一方面分析不同地形对车体升降所需驱动力矩影响。

利用上文建立的动力学模型仿真，火星车初始状态为标称高度（300 mm），首先车体下降至压紧状态（0 mm），之后再抬升至最大高度（500 mm），过程中的车厢俯仰角见图6，车厢底面离地高度见图7～8，车厢初始俯仰角-1.015 °，触地俯仰角为0°，离地500 mm时俯仰角-2.167 °。

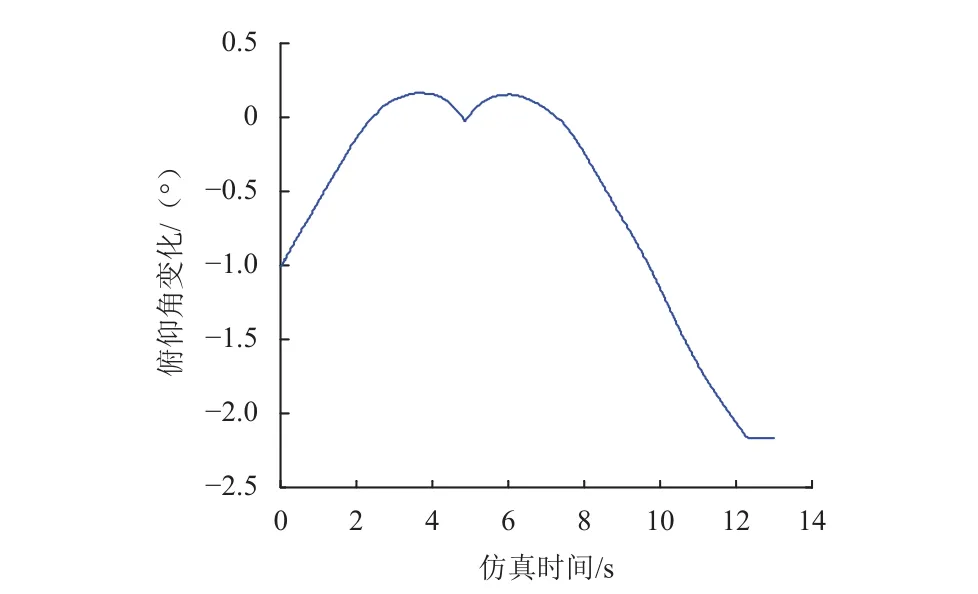
图6 车厢俯仰角Fig. 6 Elevation angle of carriage

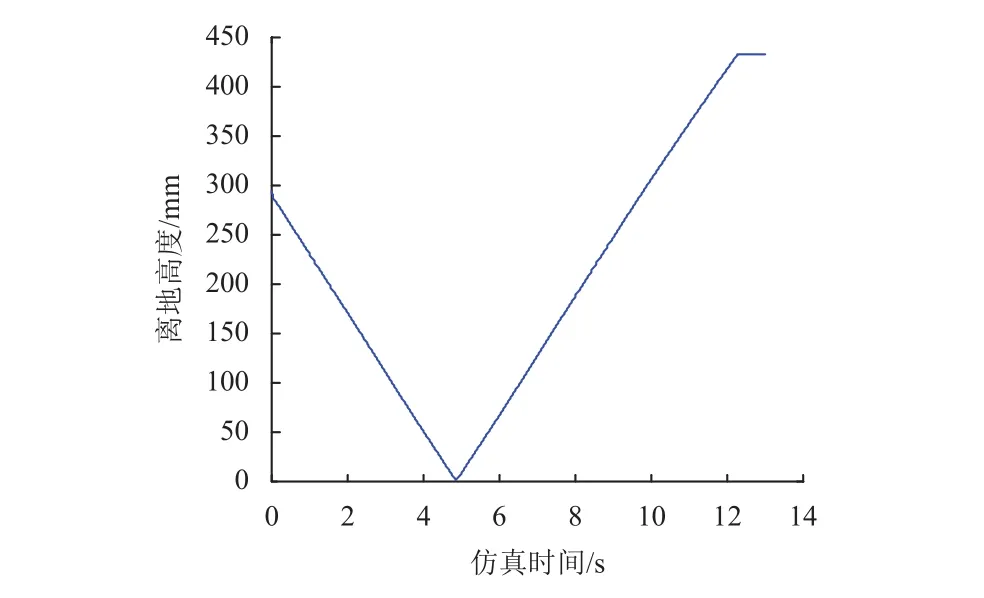
图7 车厢前端离地间隙Fig. 7 Ground clearance of front end of carriage

车体高度调整过程中主摇臂夹角调整机构最大力矩，见表4。水平地面车体高度调整主摇臂长臂和短臂所需力矩接近，而在前向坡和后向坡上进行抬升，坡下部分摇臂处所需驱动力矩明显增大，而侧向坡抬升阶段下坡处主摇臂夹角调整机构驱动力矩最大，主摇臂长臂端所需驱动力矩225 Nm，主摇臂短臂端所需驱动力矩205 Nm，因此，火星车进行车体高度调整时应考虑地形影响，尽量选取平整地面进行。

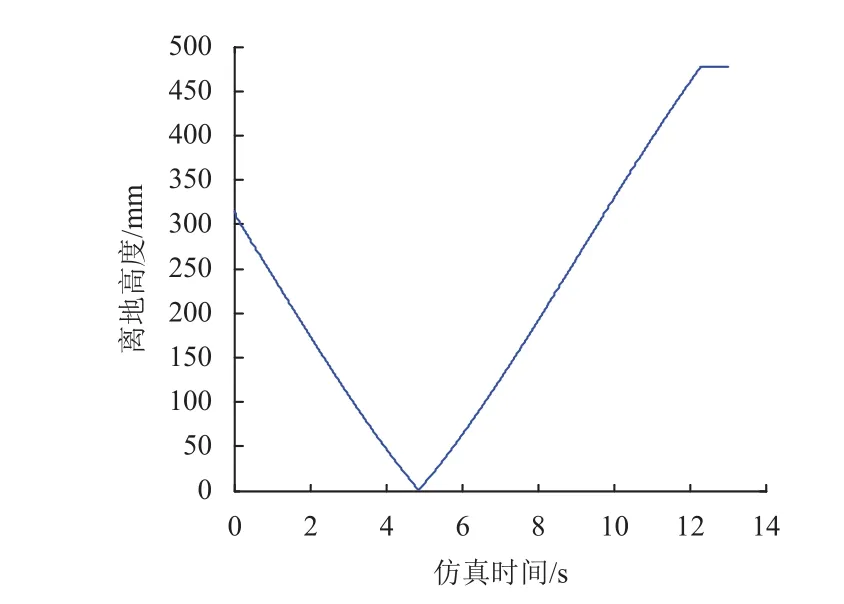
图8 车厢后端离地间隙Fig. 8 Ground clearance of back end of carriage

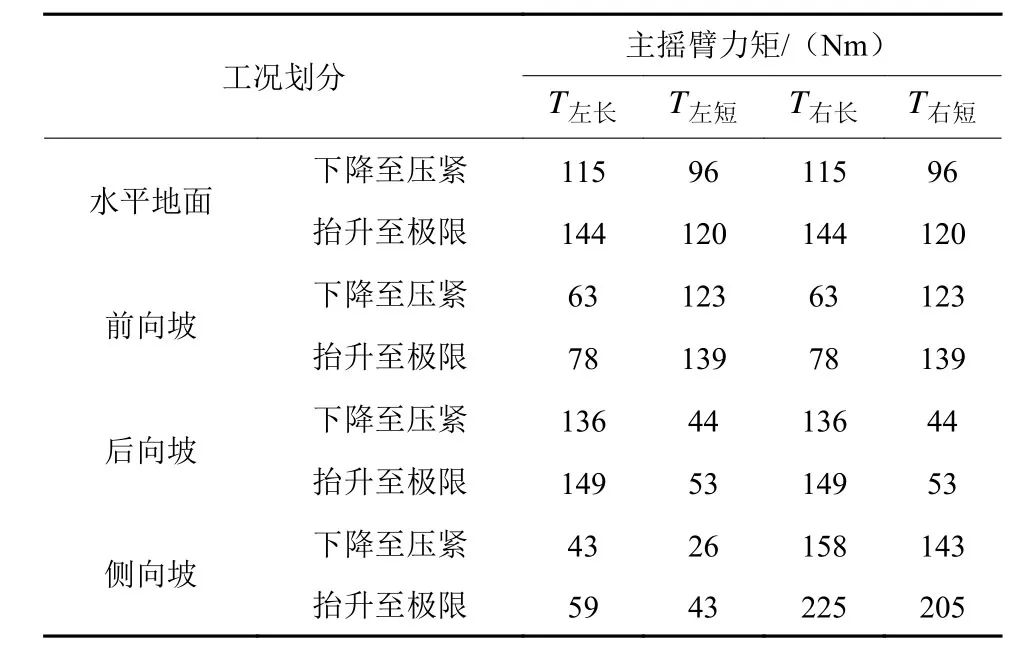
表4 夹角调整机构驱动力矩Table 4 Drive force of angle adjustment mechanism

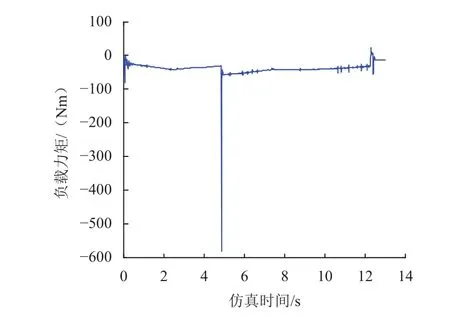
图9 左侧主摇臂长臂驱动力矩Fig. 9 Driving force of left main long arm

图9～12为侧向坡工况下车体高度调整过程中两侧主摇臂所需驱动力矩曲线，其中在4.7 s左右出现一帧较大的力矩是因为此时车体发生触地，与地面产生较大的接触碰撞力，进而引起夹角调整机构力矩突变，此数值可作为野值剔除，车体高度下降过程由于重力作用所需驱动力矩较小，而车体高度抬升过程中，随着高度增加所需驱动力矩逐渐增大，当车体高度抬升至500 mm附近时，夹角调整机构驱动力矩达到最大值。

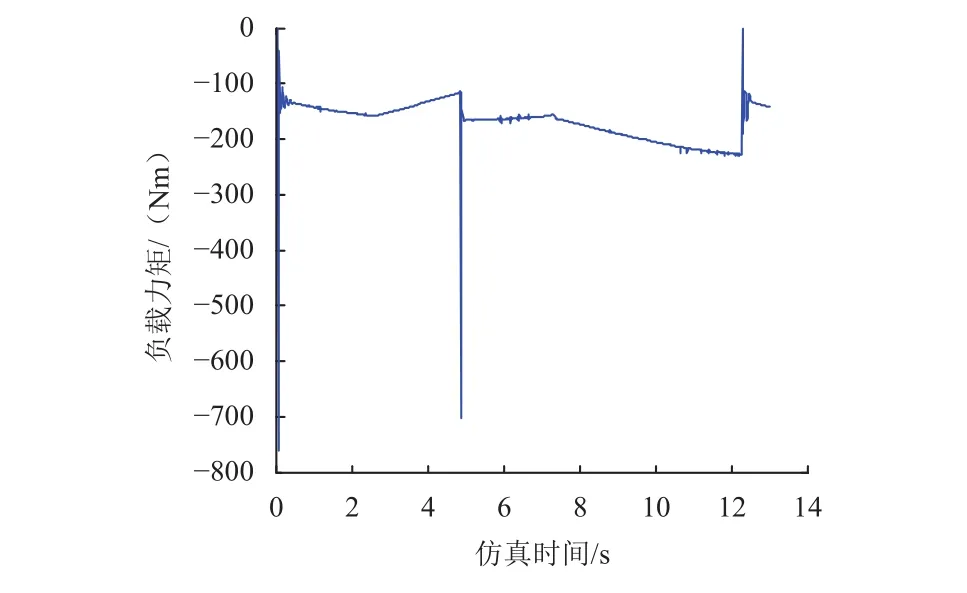
图10 右侧主摇臂长臂驱动力矩Fig. 10 Driving force of right main long arm

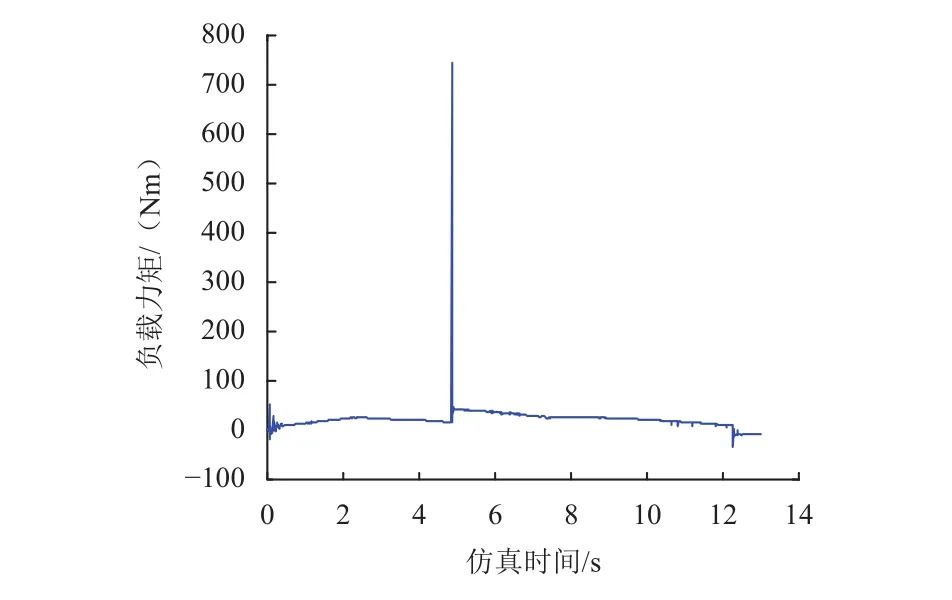
图11 左侧主摇臂短臂驱动力矩Fig. 11 Driving force of left main short arm

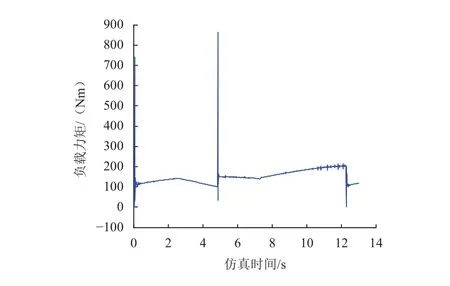
图12 右侧主摇臂短臂驱动力矩Fig. 12 Driving force of right main short arm

3.3 故障车轮抬升策略与影响分析

火星车车轮发生故障后，通过主动悬架可以将故障车轮抬起后行走，提升火星车故障下生存能力，分别考虑前轮故障、中轮故障、后轮故障等不同情况，研究不同的抬轮策略以及抬轮后行走能力进行仿真分析。

根据主动悬架移动系统的结构特征，车轮故障后抬轮策略主要有2种：一种是仅通过故障侧单侧悬架变形实现抬轮；另一种是双侧悬架同时调整，之后再单侧抬轮。通过主动悬架进行抬轮的动作过程为：①先通过车体抬升调整系统质心，前轮抬升时需将质心调整至主轴后方，后轮抬升时将质心调整至主轴前方；②抬轮侧离合器锁紧，主副摇臂间自由度被锁死；③抬轮侧夹角调整机构运动，控制前轮抬升至目标高度，前轮和后轮抬升时主摇臂长臂和短臂间夹角增大，中轮抬升时主摇臂长臂和短臂间夹角减小。

图13为通过单侧悬架变形进行前轮抬升行走示意图，从图中可看出，此种抬轮策略会导致车体出现较大的俯仰和侧倾，车厢底面高度降低明显，影响火星车的越障能力，并且移动系统摇臂受力情况不好。图14为通过双侧悬架变形进行前轮抬升行走示意图，此种策略下车体仍会出现俯仰，但侧倾很小，对火星车的越障能力影响更小，摇臂结构受力更均匀。

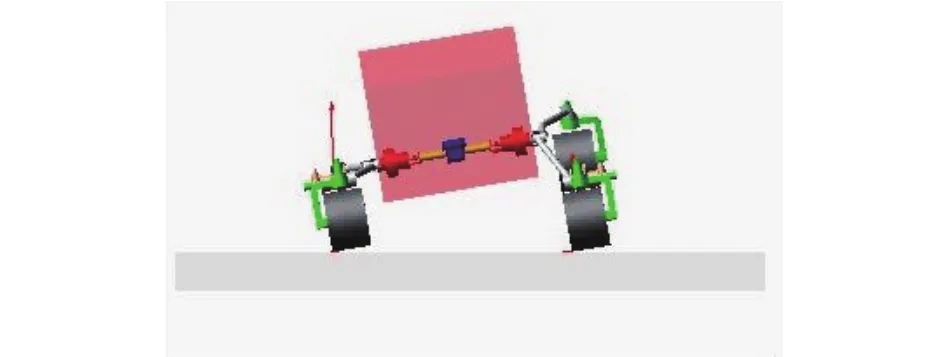
图13 单侧悬架变形抬升前轮Fig. 13 Unilateral deformation Lifting front wheel walking

图14 双侧悬架变形抬升前轮Fig. 14 Both sides deformation Lifting front wheel walking

火星车进行抬轮主要通过夹角调整机构实现，抬轮所需夹角调整机构力矩是影响火星车性能的主要指标，表5为通过双侧悬架变形实现不同轮抬升情况下夹角调整机构所需驱动力矩，前轮抬升两侧夹角调整机构所需驱动力矩基本一致，中轮抬升过程会导致车体的升高，因此所需的驱动力矩最大为217 Nm，与侧向坡车体抬升接近，并且抬轮侧明显大于非抬轮侧，而后轮抬升时，车体高度下降，重力起主动作用，所需驱动力矩小。

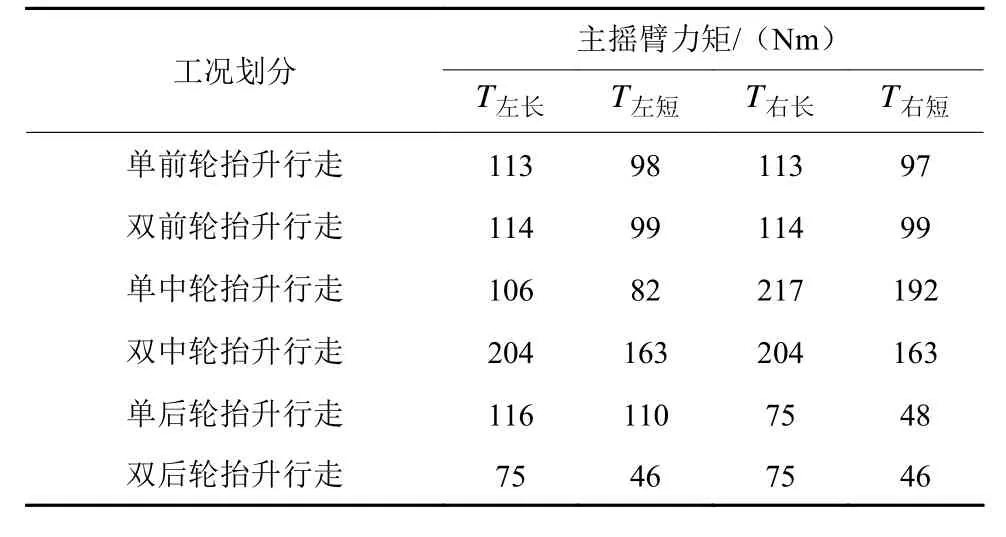
表5 夹角调整机构驱动力矩Table 5 Drive force of angle adjustment mechanism

已抬升单侧中轮为例，分析车轮抬升对火星车性能的影响。抬升中轮时车体高度为标称高度300 mm，假设右侧中轮发生故障情况，将右中轮抬升300 mm。单中轮抬升过程车体俯角变大，如图15所示，由于抬轮导致的车体俯角增加4.8 °。

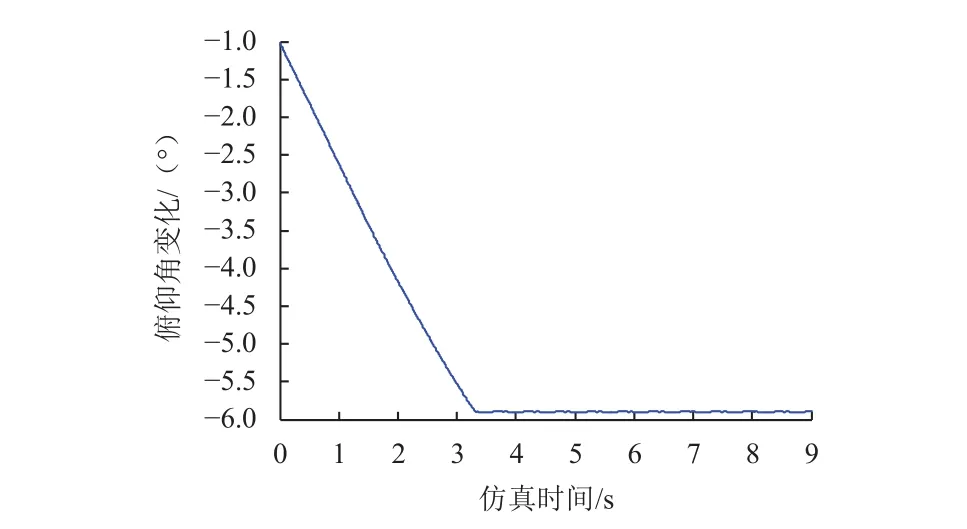
图15 单中轮抬升车厢俯仰角Fig. 15 Elevation angle of Lifting single middle wheel

图16～17为右中轮抬升过程中车体前端和后端离地间隙变化曲线，从图中可看出，右中轮抬升过程中车体前端和后端离地高度均单调增加，抬中轮不会影响火星车通过性能，但系统质心增高并且由6轮支撑变为5轮支撑，其爬坡能力和稳定性也有所下降。

图16 车厢前端离地间隙Fig. 16 Ground clearance of front end of carriage

图18～19分别为右中轮抬升过程中，右侧主摇臂长臂和短臂驱动力矩变化曲线，0～3.7 s为车轮抬升阶段，3.7～9 s为单右中轮抬升后行走阶段。从图中可看出中轮抬升所需驱动力矩较大，稳定段力矩约200 Nm，与车体抬升过程夹角调整机构驱动力矩相当，由于中轮抬升后右侧靠前后轮支撑，行走过程中摇臂结构柔性振动更大，导致夹角调整机构驱动力矩也产生周期性波动。

图17 车厢后端离地间隙Fig. 17 Ground clearance of back end of carriage

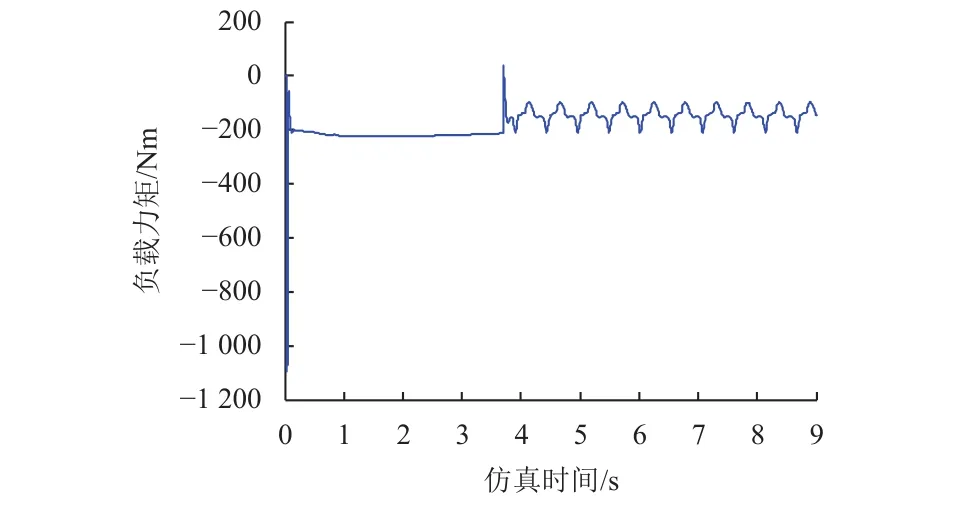
图18 右侧主摇臂长臂驱动力矩Fig. 18 Driving force of right main long arm

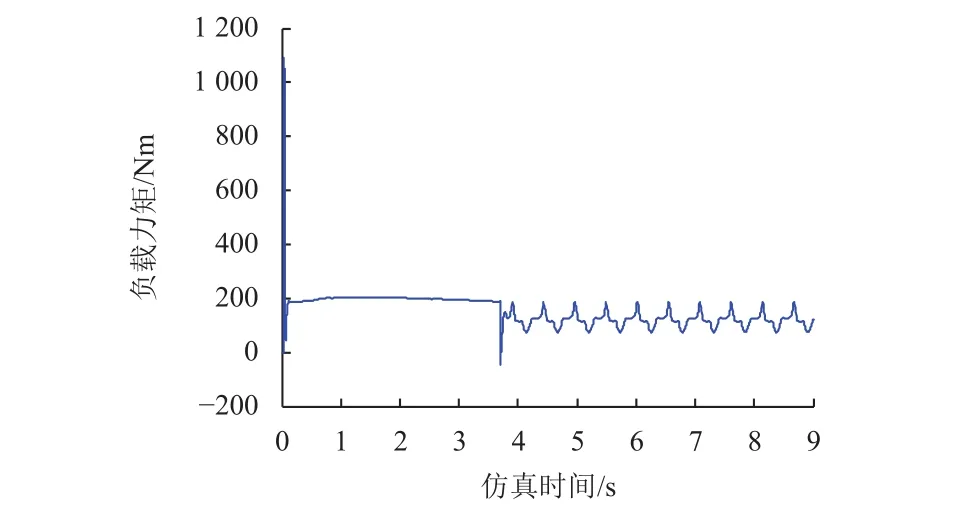
图19 右侧主摇臂短臂驱动力矩Fig. 19 Driving force of right main short arm

4 结 论

本文以中国火星车主动悬架式移动系统为研究对象，针对火星车系统的动力学建模与不同步态的控制策略和性能开展了研究，得到以下结论：

1）火星车普通步态移动过程中，越障和过坑时车轮法向力最大，并且由于火星车系统质心位于中轮上方，导致中轮承受的法向力较前后轮增加50%～100%，车轮设计和验证过程中应以中轮承载能力为基础。

2）火星车通过主动悬架具备车体高度调整能力，不同地形环境下车体升降对夹角调整机构驱动力影响较大，应尽量选取平整地面进行车体升降，可使得两侧夹角驱动力矩均衡。

3）车轮故障后抬轮行走步态下，抬轮前车体质心调整时需两侧摇臂同步进行，可有效减小由于抬轮导致的车体侧倾。

4）抬轮行走步态下，前轮和中轮抬升均不影响火星车的通过性能，而后轮抬升会导致通过性能下降；抬轮后火星车的稳定性和爬坡能力均变差，并且前轮和后轮抬升后受地面起伏颠簸影响存在抬起车轮跌落的风险。