一种改进自适应永磁同步电机永磁磁链观测算法

张 杰，韩如成

(太原科技大学电子信息工程学院，太原030024)

1 永磁同步电动机的数学模型

在同步旋转坐标(d-q坐标系)下，永磁同步电机的电压方程组可以写为:

ud=Rid+Ld·did/dt-ωLqiq

(1)

uq=Riq+Lq·diq/dt+ωLdid+ωψr

(2)

其中ud，uq分别为定子电压的d-q轴分量，Ld，Lq分别为d-q轴电感分量(对于隐极式永同步机，其电感值Ld=Lq=L)，R为定子的电阻，ω为同步转速，ψr为永磁体磁链，id，iq为为定子电流的d-q轴分量。

选取状态变量

x=(id，iq，ψrd，ψrq)T

u=(ud/L，uq/L)T

y=(id，iq)T

在永磁同步电机正常运行时，由于反馈装置会出现误差，导致电机磁链矢量相对于坐标轴产生偏差角γ.此时将会产生永磁磁链投影在d-q两轴的ψrd，ψrq分量。对应的电压方程组则改变为[1]：

ud=Rid+L·did/dt-ωLiq-ωψrq

(3)

uq=Riq+L·diq/dt+ωLid+ωψrd

(4)

把永磁磁链作为待观测量，则电压方程可以改写为：

(5)

(6)

在实际情况中，永磁磁链波动时间远远大于系统动态过程的时间，反馈装置产生的误差不会造成磁链幅值的大幅度变动，所以相对于系统状态变量，ψrd，ψrq几乎不变，于是就有方程组：

(7)

(8)

非线性系统模型和离散非线性测量方程可以写为:

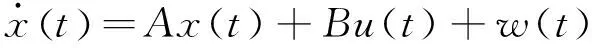
(9)

y(t)=Cx(t)+v(t)

(10)

其中，w(t)为系统噪声，v(t)为测量噪声。将状态方程离散化，T为系统采样周期[2]，则状态方程可以表示为：

B(k-1)u(k-1)+w(k-1)

(11)

x(k)=(I+T·A(k-1))x(k-1)+

(B(k-1)·u(k-1))+w(k-1))T

(12)

将上式改写为：

x(k)=A′(k-1)x(k-1)+

B′(k-1)u(k-1)+w′(k+1)

(13)

其中，各系数矩阵变换为：

A′(k-1)=(I+T·A(k-1))=

w′(k-1)=T·w(k-1)

2 UKF算法的改进

对于n维系统，UKF一般采用对称分布采样法，即要有2n+1个采样点进行UT变换[3-4]。当系统矩阵较多时，计算量就会大幅度增加，影响观测效果。所以需要在保证观测效果的前提下减少采样点。而对于最小斜度采样法，Sigma 点(采样点)的个数只需要n+2(考虑中心点)个，且该算法在采样过程中也可以保证采样数据的稳定性[5]。Sigma点(采样点)确定的具体流程如图1所示[6-7]：

图1 最小斜度采样流程Fig.1 Minimum slope sampling process

结合对状态噪声与观测干扰下的改进，双重自适应算法流程如图2所示。

图2 双重自适应算法Fig.2 Dual adaptive algorithm

3 仿真结果及分析

永磁同步电机的永磁磁链观测原理如图3所示。

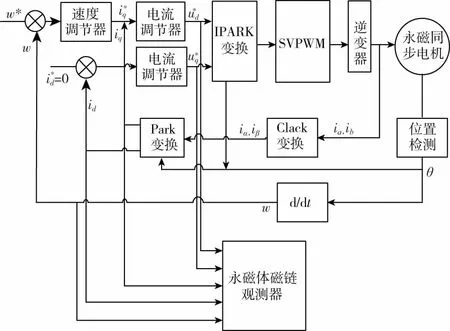
图3 仿真结构原理Fig.3 Simulation structure principle

用matlab2015a的simlink仿真软件搭建永磁同步电动机矢量控制系统的模型。永磁同步电动机的参数如表1所示。

表1 仿真模型中电机模型的主要参数Tab.1 Main parameters in the simulation model

控制环的参数如表2所示。

表2 仿真模型中控制器参数

(1)将转矩视为扰动

速度给定初始值为800 r/min，负载转矩初始值设定为0 N·m，并在0.2 s时刻分别跳跃至5 N·m，这里把负载转矩当做外部干扰来验证系统的鲁棒性。仿真结果如下。

以上仿真结果表明，在受到外部干扰时，改进后算法比无迹卡尔曼算法观测的磁链幅值波动小；稳定时间少。

图4 UKF与改进双重自适应算法观测永磁磁链观测结果Fig.4 UKF and improved dual adaptive algorithm for observing permanent magnet flux Observation

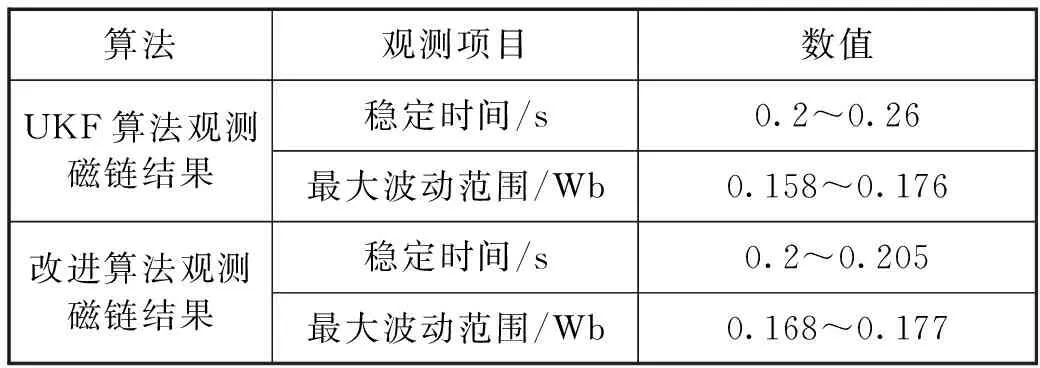
表3 两种算法对比结果

(2)将转速视为扰动

仿真中电机参数设置与表2所选用电机参数相同。负载转矩为5 N·m，速度给定初始值设定为500 r/min，并在0.2 s时刻跳跃至1 000 r/min，这里把转速当做外部干扰来验证系统的鲁棒性。仿真结果如下：

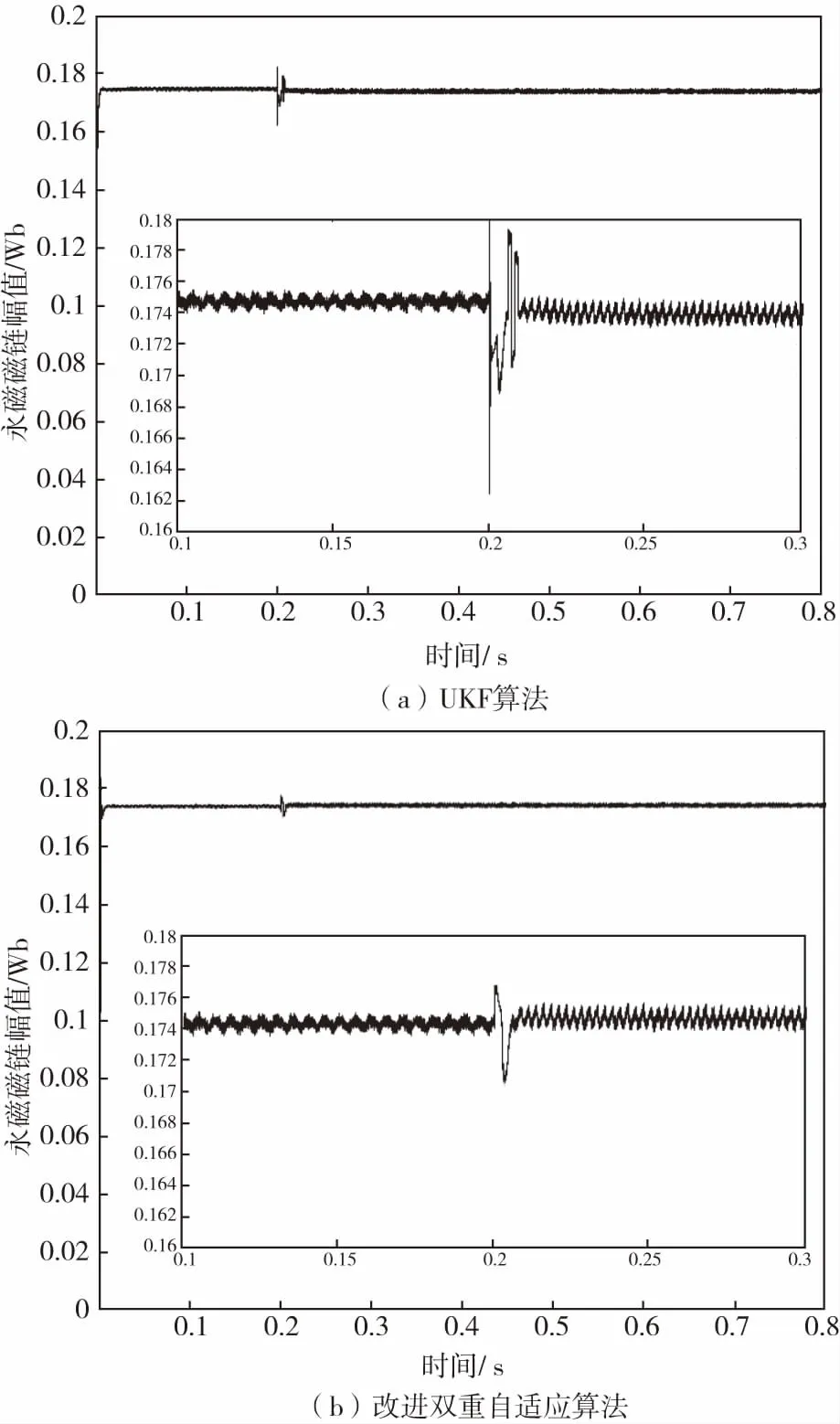
图5 UKF与改进双重自适应算法观测永磁磁链观测结果Fig.5 UKF and improved dual adaptive algorithm for observing permanent magnet observations

表4 两种算法对比结果

以上仿真结果表明，在受到外部干扰时，改进自适应卡尔曼滤波算法比无迹卡尔曼算法观测的磁链幅值波动小；稳定时间少。

为了进一步验证算法的实时性，在相同的条件下，得出两个算法的单次运行时间，为了使这个时间更具有可靠性，避免程序或者系统误差，计算时采取多次测量并取平均值，通过测量数据得到表5：

表5 两种算法运行时间

通过以上数据可以得出：改进自适应卡尔曼滤波算法的单次运算时间比UKF算法快20.56%，说明算法具有实时观测磁链参数的能力。

4 实验研究

为进一步印证前面的分析结论，运用型号为TMS320F2812的DSP处理器通过驱动电路给IPM施加触发脉冲从而控制永磁同步电机，实现了永磁同步电机控制系统。实验样机的参数与仿真中电机的参数一致，试验结果中的磁链幅值比仿真结果波动大，稳定时间也比仿真结果大，这是由于仿真条件与试验条件不同导致的。

为了验证改进前后的观测器对转矩突变扰动的响应能力，做如下实验：给定转速n=800 r/min，转矩初始值为0 N·m，在t=8 s时转矩突变到2 N·m，具体实验速度波形如图6所示。

图6 UKF算法与改进双重自适应算法观测永磁磁链幅值Fig.6 UKF algorithm and improved dual adaptive algorithm for observing permanent magnet flux amplitude

表6 UKF算法与改进双重自适应算法实验观测结果Tab.6 Experimental observations of UKF algorithm and improved dual adaptive algorithm

从实验波形中可以看出，基于改进算法的观测器在转矩突变后能快速稳定，且波动小。说明改进后的观测器对转矩突变有很好的响应能力。

为了验证改进前后的观测器对转速突变扰动的响应能力，做如下实验：给定转矩T=0(N·m)，转速初始值为n=500 r/min，在t=8 s时转速突变到n=1 000 r/min，具体实验波形如图7所示。

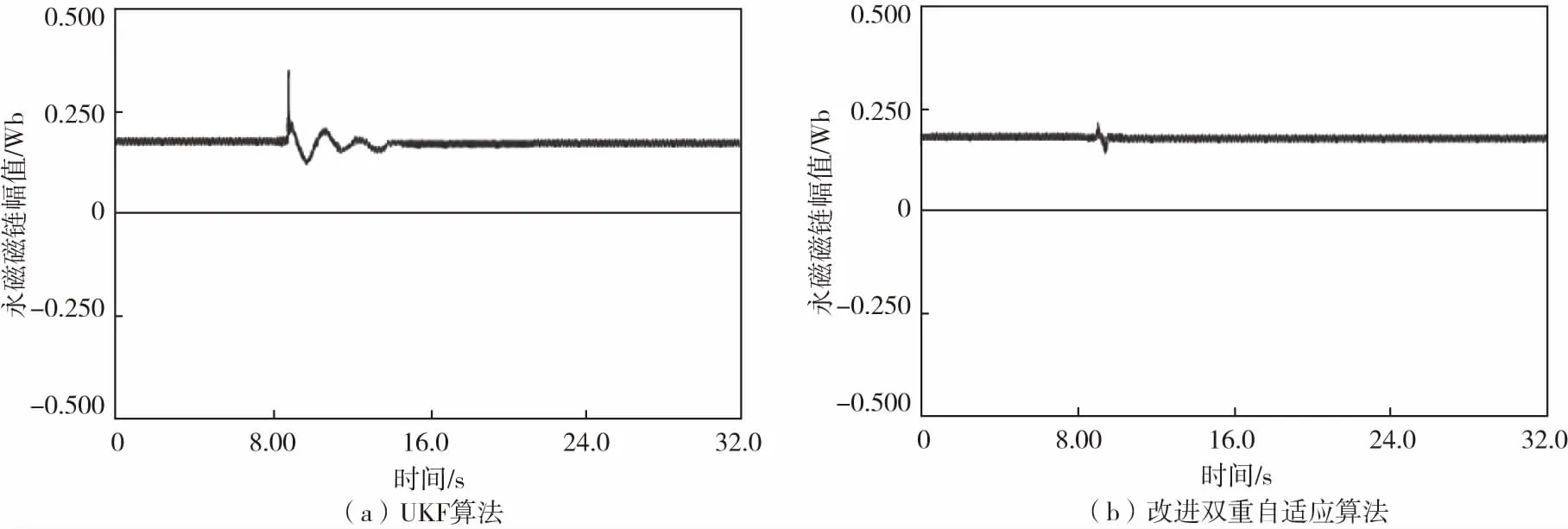
图7 UKF算法与改进双重自适应算法观测永磁磁链幅值Fig.7 UKF algorithm and improved dual adaptive algorithm for observing permanent magnet flux amplitude

表7 UKF算法与改进双重自适应算法实验观测结果Tab.7 Experimental observations of UKF algorithm and improved dual adaptive algorithm

从实验波形中可以看出，基于改进算法的观测器在转速突变后能快速稳定，且波动小。说明改进后的观测器对转速突变有很好的响应能力。

5 结论

在观测永磁磁链幅值方面，受到扰动时，仿真与实验的结果都表明改进算法比UKF算法波动幅度小，稳定时间少；在稳定性方面，对电机内部参数进行改变时，改进算法的准确度不受电机参数影响；在计算时间方面，通过对单次算法运算时间的结果对比，可以看出改进算法观测器比UKF算法观测器的运算时间少，说明改进后的算法也具有实时观测能力，并具有较强的鲁棒性。