基于轨迹间时空关联性的数据聚类算法

王 瑟，杨雨晴，蔡江辉

(太原科技大学计算机科学与技术学院，太原 030024)

随着通信技术和移动终端的迅速发展、越来越多的移动对象的活动轨迹被记录下来，如何从海量的轨迹数据中提取出有价值的信息或者模式从而为决策和服务提供支持已经成为空间信息领域研究的热点。

轨迹中的停留点是轨迹中蕴含有丰富语义信息的部分[1]，对轨迹中的停留点进行识别和提取是后续深入开展移动对象行为模式分析的基础。为了发现轨迹中的停留点，Ashbrook & Starner[2-3]在传统的K-means聚类算法的基础上加入参数领域半径r来从轨迹数据中识别停留点。文献[4]基于Hausdorff距离，设计自动选取尺度参数的相似度度量函数，构造相似度矩阵并采用谱聚类算法对轨迹进行聚类。文献[5]将轨迹进行划分，并用改进的TRACLUS算法进行轨迹聚类来分析轨迹的运动趋势。文献[6]首先用基于时间和距离的时空聚类算法提取停留点，然后用基于密度峰值快速搜索和识别停留点的算法进行聚类。文献[7]从轨迹点间的时间和空间关系考虑，将传统的DBSCAN进行改进来识别停留点。文献[8]基于大规模的出租车GPS定位和手机基站定位轨迹的基础上，研究个人和出租车群体的活动规律和活动空间特征，对手机定位数据设定速度阈值，将轨迹点进行合并构成行程，用于停留、出行的判断。文献[9]收集22位志愿者109天的手机定位数据，用于居民出行活动特征分析。结合时间与距离阈值，对获取的停留点进行提取，并考虑GPS定位精度问题，对阈值进行更改。

上述算法存在两个问题。第一，只考虑到同一条轨迹中各轨迹点的时空关联性，但轨迹间的时空关联性考虑不足。第二，利用全局唯一的距离参数来寻找轨迹中的停留点，对聚类精度产生较大影响。

根据特定个体的轨迹分析，某个移动对象可能会在相同或者不同时间段重复访问相同的位置点；根据多个个体的轨迹分析，不同移动对象也有可能所访问相同的位置点，这说明不仅轨迹点与轨迹点之间有相关性，轨迹与轨迹之间也有相关性。Gonzalez等[10]通过实验证明：个人GPS轨迹具有较高的时间和空间特征，可以通过轨迹间的时空关联性降低算法的复杂度。为了利用轨迹之间的这种时空关联性，本文提出了基于轨迹间时空关联性的数据聚类算法，充分利用已有的聚类结果降低聚类的时空开销并提升聚类精度。

本文算法包含中心代表点集生成和基于中心代表点集的聚类两个阶段。中心代表点集生成阶段首先统计各数据点r邻域内邻居点的数量，取邻居数量满足最短停留时间限制的数据点和其邻居坐标的均值作为初始中心代表点，从时间和距离约束两方面确定初始中心代表点，然后计算各邻居点与初始中心代表点的距离，将距离的最大值作为该初始中心代表点对应的半径R，最后根据最短移动时间约束合并初始中心代表点并调整半径R，直到合并结束时得到中心代表点集。当新的轨迹聚类任务到来时开始第二阶段的聚类操作，首先判断轨迹点与中心代表点集中各代表点的位置关系，删除包含在中心代表点R范围内的数据点，产生新的轨迹数据，然后对新的具有聚类价值的轨迹数据执行阶段一中的操作，最后根据聚类结果更新中心点集。

1 轨迹及其停留点

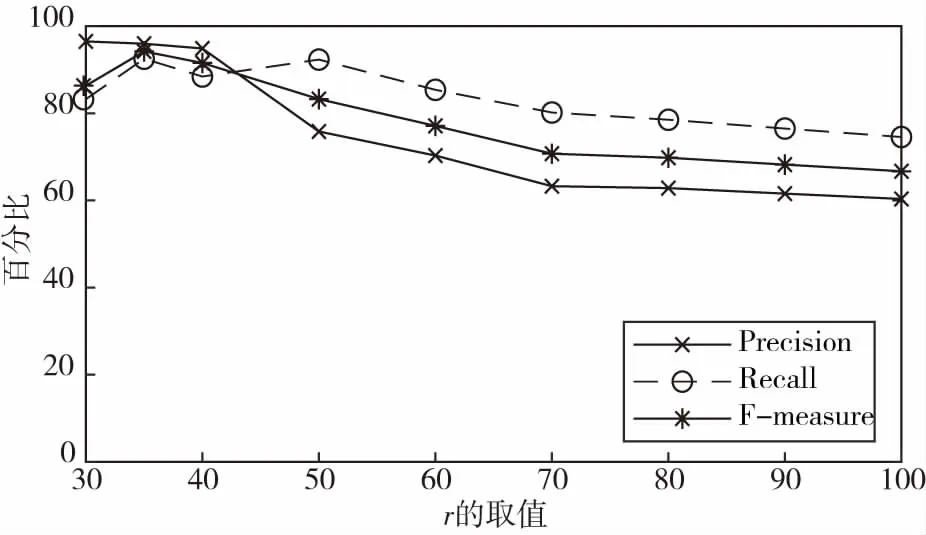
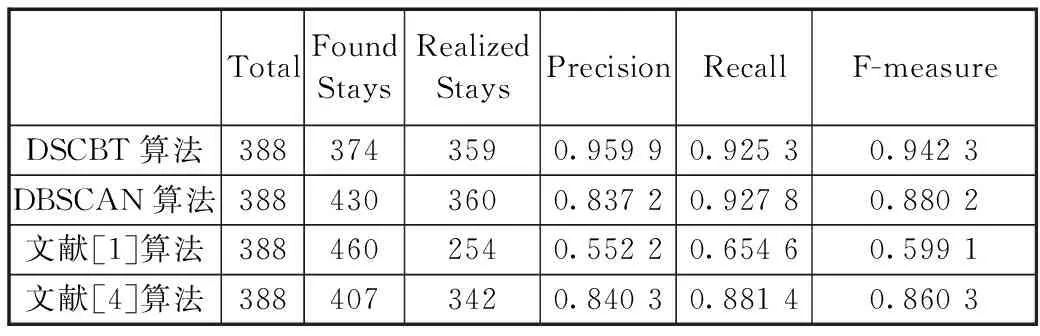
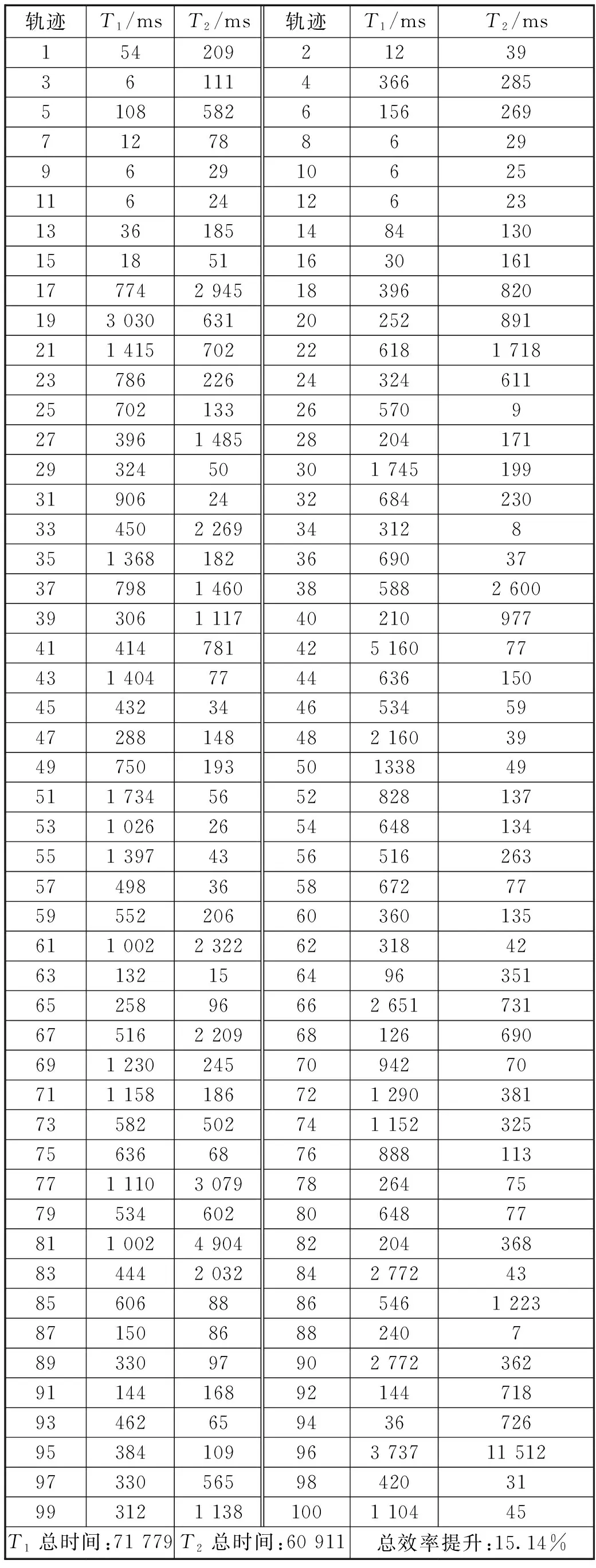
轨迹描述的是移动对象在特定时间段内移动位置随时间的变化情况，其数据在时间和空间上满足一一对应的关系。一条移动对象的轨迹可以表述为：

定义1轨迹：一条轨迹为包含n个轨迹点的时空数据序列，Traj[Id]={P0，P1，…Pn}，且Pi={(Latitude，Longitude)，Ti}，0≤i≤n，Ti

图1 移动对象的轨迹Fig.1 The trajectory of a moving object

如图1所示移动对象从家出发，到达了办公室，一段时间后从办公室出发到达了超市，在超市停留一段时间后最后回到家中。从图1可以看到，轨迹点在办公室和超市所在区域的集中程度明显大于轨迹中其余部分点的集中程度，这种在特定时间内小范围集中的数据点被称为停留点。

定义2停留点：停留点SP={Pm+1，…，Pm+i，…，Pm+p}，Pm+i={(Latitude，Longitude)，Ti}，1≤i≤p.停留点集合SP是轨迹中所有数据点的子集，其大小为p.它由满足以下条件的轨迹点构成：(1)数据点静止在原地或者在局部小范围内缓慢移动；(2)数据点在局部小范围内的停留时间持续足够长。

图1中被圈中以外的点被称为移动点，对轨迹中相邻的位置起连接作用。停留点所在的区域可能代表特定的地理位置或者在该位置曾经发生重要事件，因此，轨迹中的停留点相对于移动点来说含有更加丰富的语义特征，对轨迹中的停留点进行提取和分析对于挖掘移动对象行为和移动模式分析意义重大。

2 基于轨迹间时空关联性的数据聚类算法

根据以上思想及文献[11]，基于轨迹间时空关联性的数据聚类算法(DSCBT算法)包括算法1和算法2两个过程：

算法1:中心点集生成

输入:轨迹数据D，扫描半径r，最短停留MinDuration，最短移动MinMove

输出:中心点集CR

1.For 轨迹中的所有点

2.寻找数据点r邻域半径内的邻居并统计其所有邻居在该点r邻域内的停留时间ST；

3.If ST>MinDuration

4.将该数据点及其所有邻居的坐标均值标记为初始中心候选点，并将各邻居点与中心候选点的最大距离记为该中心候选点对应的半径R；

5.End If

6.End For

7.For 所有的初始中心候选点

8.计算其与其它未访问的候选点的距离；

9.If 距离不满足MinMove约束

10.合并中心候选点并调整合并后的中心点对应的半径，中心候选点标记为已访问；

11.合并后的中心点及其半径放入中心点集CR；

12.End If

13.中心候选点及其对用半径放入中心点集CR并标记为已访问；

14.End For

15.输出中心点集CR.

由于移动对象在某个区域的停留时间只有满足最短停留时间限制时该位置才能被视为一个真正的地理位置，同理，一段移动轨迹的移动时间必须满足了最短移动时间限制时，该段移动才是有意义的，所以本文利用轨迹中特有的时空约束来寻找轨迹中的中心代表点来近似代表轨迹中某个地理位置的中心，并将所在区域的最大距离作为该中心唯一对应的半径R，来降低全局唯一的距离阈值的影响。如算法1所示，假设轨迹中包含的数据点的数目为N，中心候选点的数目为P.在产生中心候选点阶段中需要判断数据点之间的距离是否在r领域内，所以该阶段的时间复杂度为O(N2)，合并中心候选点时的时间复杂度为O(P)，则算法1的总时间复杂度为O(N2+P).

如算法2所示，基于中心代表点集的聚类，首先将数据与CR中的元素匹配，然后删除利用CR可以划分到簇的数据点产生新的轨迹，最后对有聚类价值的新轨迹执行算法1.算法2中，SamplingRates为轨迹数据的采样时间，MinDuration/SamplingRates表示的是一个最小停留(簇)包含的最少的点数，当新轨迹中包含的数据点数超过MinDuration与SamplingRates的比值时，该新轨迹段才有可能包含有价值的信息，需要进一步的聚类处理。假设数据点数目为N，CR中元素数目为P，则利用CR聚类阶段的时间复杂度介于O(N)与O(NP)之间。在新轨迹聚类阶段，假设新轨迹中的数据点数为n(n

算法2:基于中心代表点集的聚类

输入:轨迹数据D，中心点集CR，最短停留MinDuration

输出:中心代表点集CR，簇C

1.For 轨迹中的所有点

2.计算其与CR中各点的距离；

3.If 距离小于该中心点对应的半径R

4.将数据点放入CR中该中心点代表的簇C中，

并标记该数据已访问；

5.End If

6.End For

7.For 轨迹中的所有点

8.统计未访问的数据点的数目；

9.If 统计值大于MinDuration/SamplingRates；

10.删除已经访问的轨迹点得到新的轨迹；

11.对新轨迹执行算法1；

12.End If

13.End For

14.利用聚类结果更新CR中各中心点的位置和半径。

15.输出簇C和更新后的CR

3 实验分析

3.1 数据选取

为了验证DSCBT算法的合理性和有效性，实验环境为：3.2GHz Intel Core i5处理器，8GB内存，windows 10的操作系统，以Eclipse为编程工具，利用微软亚洲研究院Geolife项目提供的轨迹数据进行了实验。该轨迹数据集由182个用户从2007年4月到2012年8月的数据形成，数据集的GPS轨迹由一系列带有时间戳的点表示，这些数据点每隔1 s～5 s或5 m～10 m被记录一次。每个点包含纬度、经度和高度信息，共包含17 621条轨迹，总距离1，292，951 km，总持续时间50，176 h.

本文从活动区域中选取轨迹点数目大于100，且经纬度范围分别在(39.88，40.10)和(116.26，116.43)之间的100条真实轨迹进行实验。

3.2 实验结果

3.2.1 参数分析

本文利用以上环境和数据集，将DSCBT算法、传统的DBSCAN算法[12]、文献[2]算法和文献[6]算法进行了对比。文献[2]算法的参数有目标聚类数k和半径r；DBSCAN聚类算法的参数有扫描半径R和邻域轨迹点个数阈值N；文献[6]算法的参数有距离阈值δd和时间阈值δt.上述两类算法的参数在相应的文献中有详细说明，根据本文数据的聚类场所和聚类活动做出了相应的调整。k和r分别为5和80 m，R和N分别为40 m和40，δd和δt分别为60 m和500 s.DSCBT算法中参数有r、MinMove、MinDuration.MinMove和MinDuration都与具体的应用有关，不同的值反应不同的聚集活动，一般来说，MinMove应该足够大，以消除噪声对实验结果的影响。不过，不建议使用太大的MinMove值，因为可能会错误地将距离相近的两段轨迹作为停留点。

在文献[6]中同样处理的是城市居民生活轨迹的数据，而文献[6]所选取的聚类簇的距离阈值的区间为(30，100).所以对于参数r的取值可以在此区间内讨论。如图2所示，r分别等于30 m，35 m，40 m，50 m，60 m，70 m，80 m，90 m，100 m时，算法聚类的结果。从图中可以看出，在r取值在(30，40)区间时算法的聚类结果较好，所以参数r的取值区间为(30，40).本文实验数据为城市居民出行数据，根据文献[13]实验研究MinMove设置为150 s.文献[14]以经验阈值为基础，对参数进行优化得到MinDuration为180 s.本文重点讨论参数r.当r取值区间为(30，40)时，综合考虑指标F-measure较高。从图中可以看出，r在35位置处的F-measure取值较高。所以本文参数r最适合的取值为35 m.

图2 r对本文算法聚类结果的影响Fig.2 Influence of r on clustering results of the algorithm

3.2.2 实验及分析

本文使用精确率、召回率和F-measure三个度量指标对上述三种算法的性能进行比较，比较结果在表1和图3中给出。在表1中，Total表示所有轨迹包含的实际停留点数目，Found Stays表示算法发现的停留点数目，Realized Stays表示算法正确识别的停留点数目，Precision和Recall分别表示精确率和召回率。

表1 三种不同聚类算法的聚类结果Tab.1 Clustering results of three different clustering algorithms

表2 时间效率对比Tab.2 Time efficiency comparison

图3 四种不同聚类算法的聚类结果Fig.3 Clustering results of four different clustering algorithms

如表1和图3所示，虽然DSCBT算法和DBSCAN算法的召回率很接近，但DSCBT算法的精确率明显高于DBSCAN算法的精确率。为了权衡精确率和召回率两个指标，本文计算了F-measure指标来综合考虑。四个算法的F-measure指标分别为：0.942 3，0.880 2，0.599 1，0.860 3.这表明文献[2]算法与其他三种算法相比，聚类效果不理想。DSCBT算法较DBSCAN算法有所提升。

为了进一步验证DSCBT算法的时间效率，本文分别对DSCBT算法和文献[6]算法的执行时间进行了考察。如表2所示，100条轨迹中，45条轨迹在使用DSCBT算法后的时间效率得到了不同程度的提升。其中时间点在中心点集中的比例越大。另外55条轨迹在使用DSCBT算法后时间效率有不同程度降低。时间效率降低越多说明该轨迹中停留的位置信息只有少部分包含或者完全没有被包含在中心点集中，中心点集匹配阶段消耗的时间长，使得该轨迹整体聚类时间增加。

通过以上分析，一方面可以看出移动轨迹之间是有关联的，移动对象重复访问某些地理位置的机率是很高的，不考虑轨迹与轨迹之间的时空关联将有可能错过某些重要信息，造成时间和空间的极大浪费。另一方面可以得出利用中心点集合进行轨迹数据聚类能够充分利用轨迹与轨迹之间的时空关联性，从而降低轨迹聚类的时空开销。综上所述，本文提出的DSCBT算法能够有效解决重复聚类相同地理位置带来的时空浪费问题，从而降低轨迹聚类的时空开销。

4 结论

针对现有轨迹聚类算法对轨迹之间时空关联性考虑不足以及全局唯一距离阈值带来的时间复杂度高以及聚类精度低的问题，本文提出了一种基于轨迹间时空关联性的数据聚类算法。根据时间和距离限制建立中心代表集，然后在根据中心代表集进行聚类。通过实验验证了该算法的性能，结果表明该方法的在降低时间复杂度和提高聚类精度方面有较好的效果。